Hassani S. Mathematical Methods: For Students of Physics and Related Fields
Подождите немного. Документ загружается.


266 Infinite Series
Then the induction principle ensures that the statement (equation) holds for
all positive integers.
Multiply both sides of Equation (9.7) by a + b to obtain
(a + b)
m+1
=
m
k=0
m
k
a
m−k+1
b
k
+
m
k=0
m
k
a
m−k
b
k+1
.
Now separate the k = 0 term from the first sum and the k = m term from
the second sum:
(a + b)
m+1
= a
m+1
+
m
k=1
m
k
a
m−k+1
b
k
+
m−1
k=0
m
k
a
m−k
b
k+1
let k = j − 1 in this sum
+b
m+1
= a
m+1
+
m
k=1
m
k
a
m−k+1
b
k
+
m
j=1
m
j −1
a
m−j+1
b
j
+ b
m+1
.
The second sum in the last line involves j. Since this is a dummy index, we
can substitute any symbol we please. The choice k is especially useful because
then we can unite the two summations. This gives
(a + b)
m+1
= a
m+1
+
m
k=1
(
m
k
+
m
k − 1
)
a
m−k+1
b
k
+ b
m+1
.
If we now use
m +1
k
=
m
k
+
m
k − 1
which the reader can easily verify, we finally obtain
(a + b)
m+1
= a
m+1
+
m
k=1
m +1
k
a
m−k+1
b
k
+ b
m+1
=
m+1
k=0
m +1
k
a
m−k+1
b
k
.
Mathematical induction is also used in defining quantities involving inte-
gers. Such definitions are called inductive definitions. For example, induc-
inductive
definitions
tive definition is used in defining powers: a
1
= a and a
m
= a
m−1
a.
9.3 Infinite Series
An infinite series is an indicated sum of the members of a sequence {a
k
}
∞
k=1
.
This sum is written as
a
1
+ a
2
+ a
3
+ ···≡
∞
k=1
a
k
≡
∞
j=1
a
j
≡
∞
n=1
a
n
≡
∞
♣=1
a
♣
,

9.3 Infinite Series 267
where we have exploited the freedom of choice in using the dummy index as
emphasized in the previous section.
Box 9.3.1. Associated with an infinite series is the sequence of partial
sums {S
n
}
∞
n=1
with S
n
= a
1
+ a
2
+ ···+ a
n
=
n
k=1
a
k
.Aseriesiscon-
vergent (divergent) if its associated sequence of partial sums converges
(diverges).
For a convergent series the nth member of the sequence of partial sums will
be a good approximation to the series if n is large enough. This is a simple
but important property of the series that is very useful in practice. It should
be clear that the convergence property of a series is not affected by changing
a finite number of terms in the series. Convergent series can be added or
multiplied by a constant to obtain new convergent series. In other words, if
∞
n=1
a
n
= A and
∞
n=1
b
n
= B,then
∞
n=1
(a
n
± b
n
)=A ±B, r
∞
n=1
a
n
= rA,
for any real number r.
9.3.1 Tests for Convergence
When adding, subtracting, or multiplying finite sums, no problem occurs
because these operations are all well defined for a finite number of terms.
However, when adding an infinite number of terms, no operation on the infinite
sum will be defined unless the series converges. It is therefore important to
have criteria to test whether a series converges or not. We list various tests
which are helpful in determining whether an infinite series is convergent or
not.
The nth Term Test
If lim
n→∞
a
n
=0,then
∞
n=1
a
n
diverges. This is easily shown by looking at if the infinite
series is to
converge, its nth
term must
approach zero.
Butthatbyitself
is not enough for
convergence!
the difference S
n
−S
n−1
and noting that it is simply a
n
, and that if the series
converges, then this difference must approach zero by the Cauchy criterion.
Thus none of the following series converges:
∞
n=1
n
n +1
,
∞
k=1
(−1)
k
k − 1
5k − 1
,
∞
j=1
(−1)
j
,
∞
m=1
m
2
− 10
8m
2
+1
.
On the other hand, the series
∞
n=1
n
n
2
+1
,
∞
k=1
(−1)
k
1
k
,
∞
j=1
1
j
,
∞
m=1
1
m
2
,
268 Infinite Series
may or may not converge: The approach of a
n
to zero does not guarantee
the convergence of the series. In fact, the first and third of the series above
diverge while the second and last converge.
Box 9.3.2. Do not confuse the convergence of an infinite series with the
convergence of its nth term. If the nth term converges to anything but
zero, the series will not converge!
Absolute Convergence
If
∞
n=1
|a
n
| converges, so does
∞
n=1
a
n
. The series is then said to be abso-absolute
convergence
lutely convergent. For example, the series
∞
k=1
(−1)
k
/2
k
converges because
∞
k=1
1/2
k
converges. However, although the series
∞
k=1
1/k can be shown
to diverge,
∞
k=1
(−1)
k
/k is known to converge.
Comparison Test
If |a
n
|≤b
n
for large enough values of n and
∞
n=1
b
n
converges, then
∞
n=1
a
n
is absolutely convergent and
∞
n=1
a
n
≤
∞
n=1
b
n
. On the other hand, if
a
n
≥ b
n
≥ 0 for large values of n and
∞
n=1
b
n
diverges, then so does
∞
n=1
a
n
.
Integral Test
This is probably the most powerful test of convergence for infinite series.
Assume that lim
n→∞
a
n
= 0, so that the series is at least a candidate for
convergence. Now find a function f which expresses a
n
, i.e., such that f (n)=
a
n
, and assume that f(n) decreases monotonically for large values of n.Then
Theorem 9.3.1. The series
∞
n=1
a
n
converges if and only if the integral
∞
c
f(t) dt exists and is finite for some real number c>1.
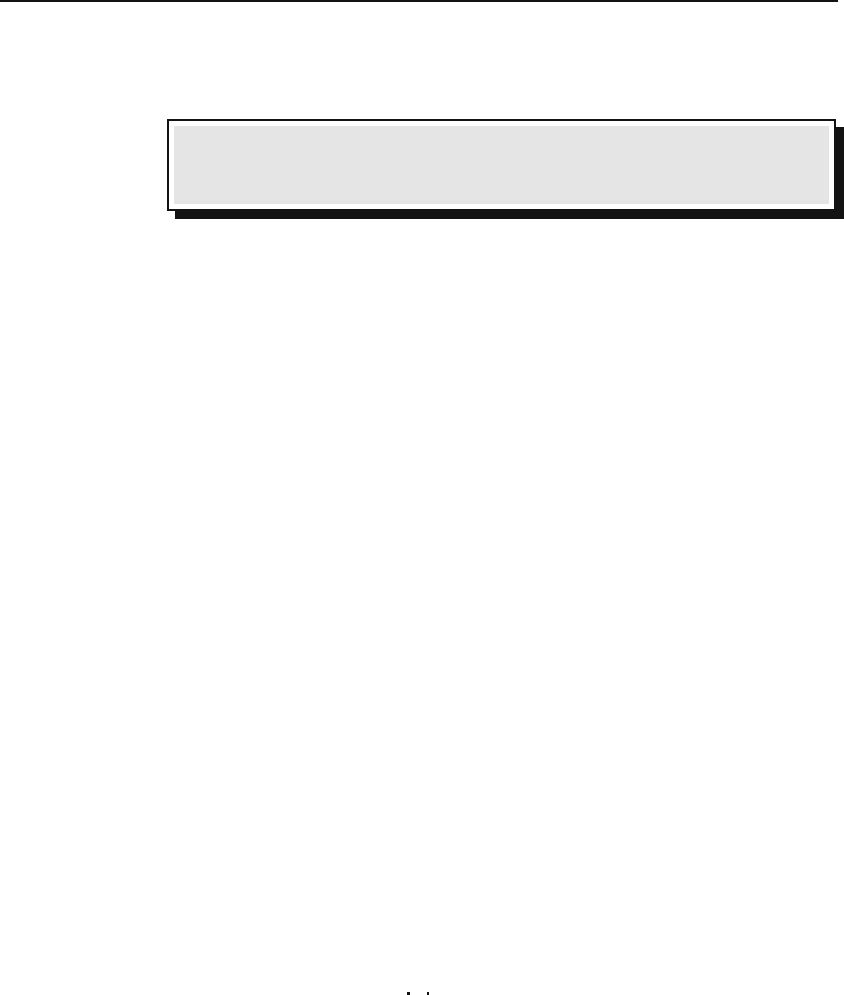
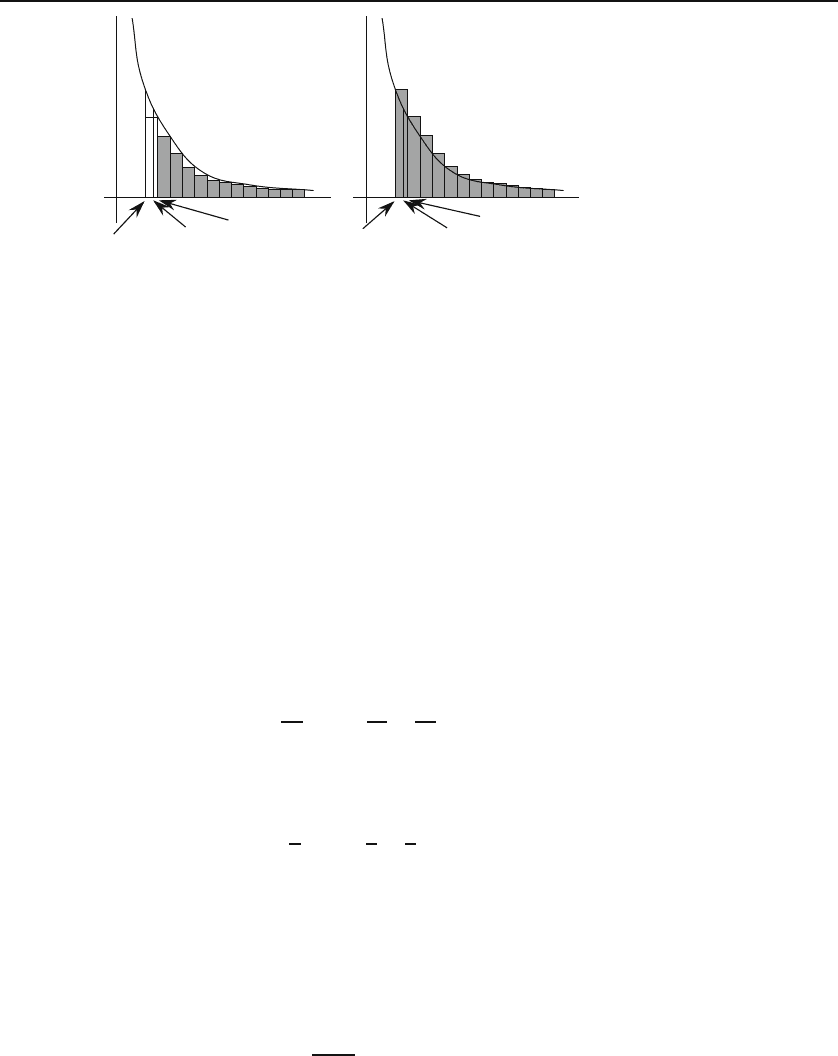
To see this, refer to Figure 9.2 and suppose that c lies between two con-
secutive positive integers m and m + 1. Since the convergence or divergence
of a series is not affected by the removal of a finite number of terms of the
series, we are allowed to consider either the series
∞
k=m
a
k
or
∞
k=m+1
a
k
.
Figure 9.2(a) compares the area under the curve f (t) with the shaded area
which is the sum of the areas of an infinite number of rectangles each of height
f(k)=a
k
for some positive integer k larger than (or equal to) m +1. The
width of all rectangles is unity. The shaded area A is therefore
A =
∞
k=m+1
f(k)
=a
k
Δt =
∞
k=m+1
a
k
·1=
∞
k=m+1
a
k
.
It is clear from Figure 9.2(a) that
A<
#
∞
c
f(t) dt ⇒
∞
k=m+1
a
k
<
#
∞
c
f(t) dt.
9.3 Infinite Series 269
t = m
t = c
t = m +
1
t = m
t = c
t = m +
1
)
b
()a(
f (t)
f (t)
t
t
Figure 9.2: The area under the curve (a) bounds, and (b) is bounded by, the infinite
sum obtained from the series by removing a finite number of terms. This finite number
of terms is the first m terms for (a) and the first m − 1 terms for (b).
Similarly, Figure 9.2(b) shows that
∞
k=m
a
k
is larger than the area under the
curve. We thus can write
∞
k=m+1
a
k
<
#
∞
c
f(t) dt <
∞
k=m
a
k
.
Hence, if the integral is finite
∞
k=m+1
a
k
(being smaller than the integral)
is also finite and the series converges. If, on the other hand, the integral is
infinite then
∞
k=m
a
k
(being larger than the integral) diverges.
The integral test leads directly to the observation that the Riemann zeta
function, also called the harmonic series of order p defined by
Riemann zeta
function or
harmonic series of
order p
ζ(p) ≡
∞
k=1
1
k
p
=1+
1
2
p
+
1
3
p
+ ··· (9.9)
converges for p>1 and diverges for p ≤ 1. In particular,
ζ(1) =
∞
k=1
1
k
=1+
1
2
+
1
3
+ ··· ,
called simply the harmonic series, diverges.
harmonic series
Ratio Test
Consider the series
∞
n=1
a
n
.Ifa
n
= 0 for large enough n and
lim
n→∞
a
n+1
a
n
= R,
then the series is absolutely convergent if R<1 and is divergent if R>1.
270 Infinite Series
The terms that we choose for the ratio test need not be consecutive. To
see this, note that
lim
n→∞
a
n+2
a
n
= lim
n→∞
a
n+2
a
n+1
· lim
n→∞
a
n+1
a
n
=
lim
n→∞
a
n+1
a
n
2
.
In going to the last equality, we have used the following:
lim
n→∞
a
n+2
a
n+1
= lim
(m−1)→∞
a
m+1
a
m
= lim
m→∞
a
m+1
a
m
= lim
n→∞
a
n+1
a
n
,
wherewehavesubstitutedm = n + 1 and used Equation (9.3) and the fact
that m →∞if and only if (m − 1) →∞. It now follows that
lim
n→∞
a
n+1
a
n
=
"
lim
n→∞
a
n+2
a
n
and the LHS will be less than or greater than one if the term inside the square
root sign is. In fact, one can generalize the above argument and state that
the series is convergent (divergent) if
lim
n→∞
a
n+j
a
n
=
lim
n→∞
a
n+1
a
n
j
(9.10)
is less than (greater than) one for any finite j.
The Riemann zeta function can sharpen the ratio test of convergence to
allow for certain cases in which the ratio is one. Instead of taking the complete
limit, we approximate the ratio of consecutive terms for the Riemann zeta
function to first order in 1/n. This yields
a
n+1
a
n
=
n
n +1
p
=
n +1
n
−p
=
1+
1
n
−p
≈ 1 −
p
n
,
where we used the binomial expansion formula, to which we shall come back
[see Equation (10.15)]. We know that such a ratio leads to a convergent series
if p>1andtoadivergentseriesifp ≤ 1. Therefore, we obtain
Theorem 9.3.2. (Generalized Ratio Test). If the ratio of consecutive
terms of a series satisfies
a
n+1
a
n
→ 1 −
p
n
, then the series converges if p>1
and diverges if p ≤ 1.
Alternating Series Test
An alternating series
a
1
− a
2
+ a
3
− a
4
+ ···=
∞
j=1
(−1)
j+1
a
j
,a
j
> 0,
converges if lim
j→∞
a
j
= 0, and if there exists a positive integer N such that
a
k
>a
k+1
for all k>N.

9.3 Infinite Series 271
Example 9.3.3. Ausefulseriesisthegeometric series: geometric series
b + bu + bu
2
+ bu
3
+ ···=
∞
k=0
bu
k
.
We claim that this series converges to b/(1 − u)if|u| < 1, and diverges if |u|≥1.
To show this, let S
n
represent the sum of the first n terms, so that {S
n
}
∞
n=0
is the
sequence of partial sums. We calculate S
n
as follows. First note that
S
n
=
n
k=0
bu
k
⇒ uS
n
=
n
k=0
bu
k+1
.
Next separate the zeroth term from the rest of S
n
and rewrite it as
S
n
= b +
n
k=1
bu
k
= b +
n−1
m=0
bu
m+1
= b +
n−1
k=0
bu
k+1
,
where in the second equality, we changed k to m = k − 1 and in the last equality
we changed the dummy index back to k. Subtracting uS
n
from S
n
,weobtain
S
n
− uS
n
=(1−u)S
n
= b +
n−1
k=0
bu
k+1
−
n
k=0
bu
k+1
= b +
n−1
k=0
bu
k+1
−
n−1
k=0
bu
k+1
+ bu
n+1
= b − bu
n+1
or
S
n
=
b − bu
n+1
1 − u
.
It is now clear that u
n+1
→ 0forn →∞only if |u| < 1. For |u| > 1, the series
clearly diverges. For |u| = 1 the partial sum is either S
n
= nb (when u =1),which
diverges for any nonzero b,orS
n
= b
∞
n=0
(−1)
n
, which bounces back and forth
between +b and −b, and never converges. So the series diverges for |u|≥1
For example, if b =0.3andu =0.1, then the series gives
0.3+0.3 × 0.1+0.3 ×0.01 + ···=0.33333 ···=
0.3
1 − 0.1
=
1
3
.
For b = 1 the series gives
1+u + u
2
+ ···=
1
1 − u
=(1− u)
−1
, (9.11)
which can be thought of as the binomial expansion when the power is −1. As we
shall see in Section 10.1, there is a generalization of binomial expansion for any real
power.
The result of Example 9.3.3 is important enough to be summarized:
Box 9.3.3. The series b + bu + bu
2
+ bu
3
+ ···=
∞
k=0
bu
k
is called the
geometric series. It converges to b/(1 − u) if |u| < 1, and diverges if
|u|≥1.

272 Infinite Series
Example 9.3.4. Another example of a series used often is
1+1+
1
2!
+
1
3!
+ ···=
∞
k=0
1
k!
.
The ratio test shows only that the series converges, but the comparison test gives
us more information. In fact, since 1/n! ≤ 1/2
n−1
for n ≥ 1, we conclude that
1+
1
2!
+
1
3!
+ ···≤1+
1
2
+
1
2
2
+
1
2
3
+ ··· .
But the RHS is the geometric series with u =1/2whichisknowntoconvergeto2.
We thus obtain the upper bound to our series:
2 ≤
∞
k=0
1
k!
≤ 3.
It is well known that the series converges to e =2.718281828 ···.
Example 9.3.5. If one alternates the sign of the terms in the harmonic series,
one obtains the series
1 −
1
2
+
1
3
−
1
4
+ ···
which is convergent by the alternating series test. In fact, we shall show in Exampleconditional
convergence 9.4.4 that the series converges to ln 2. Note that the series is not absolutely conver-
gent. A convergent series that does not converge absolutely is called conditionally
convergent.
Historical Notes
The invention of calculus motivated several other areas of investigation in math-
ematics. One of these areas was infinite series. For example, it was not always
possible to find a closed formula for the integral of a function. So, it was common to
expand the integrand in powers of the variable and integrate the resulting infinite
series. No question was asked as to the legitimacy of the operations performed.
In fact, Newton, Leibniz,andEuler regarded infinite series as an extension of the
algebra of polynomials, and they did not realize that new problems would arise if
a finite sum were extended to an infinite series. However the apparent difficulties
that did arise caused them occasionally to bring up the question of convergence and
divergence.
Some mathematicians of the seventeenth century had observed the difference
between convergence and divergence. In 1668 Lord Brouncker, while studying the
relation between ln x and the area under y =1/x, demonstrated the convergence
of the series for ln 2 and ln(
5
4
) by comparison with a geometric series. Newton and
James Gregory, who made much use of the numerical values of series to calculate
logarithmic and other function tables and to evaluate integrals, were aware that the
sum of a series can be finite or infinite. The terms “convergent” and “divergent”
were actually used by Gregory in 1668, but he did not develop the ideas.
Leibniz, too, felt some concern about convergence and noted in a letter of Oc-
tober 25, 1713 to John Bernoulli what is now a theorem that we call the alternating
series test. Maclaurin used series as a regular method for integration. He recognized
9.3 Infinite Series 273
that the terms of a convergent series must continually decrease and become less than
any given quantity no matter how small.
D’Alembert also distinguished convergent from divergent series. In his article
“S´erie” in the Encyclop´edie he describes a convergent series as that which approaches
a finite value and consequently has terms that keep diminishing. In this same
volume, d’Alembert gave a test for the absolute convergence of the series
∞
k=1
a
k
,
namely, if for all k>N,theratio|a
k+1
/a
k
| <rwhere r is a positive number
independent of k and less than 1, the series converges absolutely.
Edward Waring (1734–1798), Lucasian professor of mathematics at Cambridge
University, held advanced views on convergence. He showed that the harmonic series
of order p converges if p>1 and diverges if p<1. He also gave the well-known test
for convergence and divergence, now known as the ratio test.
9.3.2 Operations on Series
It has already been mentioned that convergent series can be added, subtracted,
and multiplied by a constant. There are other important operations one can
perform on convergent series. These operations may be “obvious” for finite
sums, but they have to be justified for infinite series. In fact, performing such
obvious operations on divergent series leads to contradictory results.
One such operation is grouping:
grouping of
convergent series
Box 9.3.4. One can group the terms of a finite sum or a convergent
infinite series in any way one desires, and the sum will not change.
The operation of grouping is essentially putting parentheses around a collec-
tion of terms of the series (or the sum), adding the terms inside each parenthe-
ses first, and then adding the results. This is simply the associative property
of addition. It turns out that this associative property of addition does not
apply to divergent infinite series.
2
For example,
∞
m=0
(−1)
m
gives an infinite
number of zeros if every +1 is grouped with one −1. On the other hand, the
same series can be grouped such that the first +1 is set aside and the rest of
the terms are paired. The result would then be a +1 with an infinite number
of zeros.If a series is divergent and not bounded, so that the sum is infinite,
warning!
rearranging terms
is not, in general,
allowed!
then any grouping of terms gives infinity.
Another operation is the rearrangement oftermsofaseries. Thisisthe
commutative property of addition:
Box 9.3.5. If a series is absolutely convergent then the rearrangement
of terms does not change either the nature of convergence or the limit of
the series. A conditionally convergent series does not share this property.
2
Caution is to be exercised not to move the terms around, as this will, in general, affect
the sum as explained in the property of rearrangement described below.
274 Infinite Series
To see the importance of absolute convergence, consider the alternating series
∞
k=1
(−1)
k+1
/k—which converges conditionally to ln 2—and rearrange terms
as follows:
∞
k=1
(−1)
k+1
k
=1+
1
3
+
1
5
+ ···−
1
2
1+
1
2
+
1
3
+ ···
!
=1+
1
2
+
1
3
+
1
4
+
1
5
+ ···−
1
2
−
1
4
−
1
6
−···
−
1
2
1+
1
2
+
1
3
+ ···
!
=1+
1
2
+
1
3
+
1
4
+
1
5
+ ···−
1+
1
2
+
1
3
+ ···
!
=0,
where in the second line, terms with even denominators have been added
and subtracted with the positive ones interspersed among terms with odd
multiplication of
two series
denominators.
The third operation is multiplication of two series. As for rearrange-
ment,
Box 9.3.6. Multiplication is defined only for absolutely convergent series:
If the two series
∞
k=1
a
k
and
∞
j=1
b
j
are absolutely convergent, then
their product (
∞
k=1
a
k
) ·(
∞
j=1
b
j
) ≡
∞
k=1
∞
j=1
a
k
b
j
≡
∞
i=1
c
i
is also
absolutely convergent.
The last series is a rearrangement of the terms a
k
b
j
into a single term c
i
.
This rearrangement makes it necessary for the original series to be absolutely
convergent.
9.4 Sequences and Series of Functions
The infinite series of the last section are useful when we want to approximate
anumber,suchase or ln 2 by a (large) sum of other (rational, decimal) num-
bers. Physics, however, deals with functions as well as numbers. It is therefore
useful to know how to approximate functions in terms of “elementary” func-
tions. In this section we shall investigate the possibility of expressing a given
function in terms of a series of functions. Since functions give numbers once
their arguments are assigned a value, many of the ideas developed in the
preceding two sections will be employed.
Suppose for each natural number n there is a function f
n
(x). Then, the
set {f
n
(x)}
∞
n=1
is called a sequence of functions. Just as in the case ofsequence of
functions
sequences of numbers, we need to address the question of the convergence
of the sequence of functions. This reduces to the question of convergence of
ordinary numbers once we substitute values for x. Variation of f
n
(x)withx
opens up the possibility of convergence for some values of x and divergence
for others. For instance, the sequence {x
n
}
∞
n=1
converges for −1 <x<1and
diverges for all other values of x.

9.4 Sequences and Series of Functions 275
More interesting than sequences of functions are series of functions: series of functions
f
1
(x)+f
2
(x)+f
3
(x)+···=
∞
k=1
f
k
(x).
The nth partial sum of such a series is
S
n
(x)=f
1
(x)+f
2
(x)+···+ f
n
(x)=
n
j=1
f
j
(x).
The convergence of a series of functions
∞
k=1
f
k
(x) depends on x.Forex-
ample, the series may converge for x =0.35. This means that the series of
numbers
∞
k=1
f
k
(0.35) converges, i.e., there exists a real number s such that
for every there exists an N with the property that |
n
k=1
f
k
(0.35) − s| <
whenever n>N. It should be clear that an N that works for one value of
x—here 0.35—and , may not work for other values of x and .Thus,N
depends on x and , and this dependence is denoted by N(x, ).
We can imagine making a table with one column consisting of the values
of x and a second column consisting of the corresponding limits of the series
ofnumberswhosetermsaref
n
evaluated at the value of x. The table then
defines a real-valued function, say S(x), which is called the limit of the series
of functions,andonewrites
S(x) = lim
n→∞
S
n
(x) ≡
∞
k=1
f
k
(x). (9.12)
We have already seen examples of series of functions: the geometric series
∞
n=0
u
n
—convergent for |u| < 1—in which the terms are functions of u
with f
n
(u)=u
n
, and the Riemann zeta function (or harmonic series of degree
p)—convergent for |p| > 1—in which the terms were functions of p with
f
n
(p)=1/n
p
.
In general, the sum in Equation (9.12) may converge only for a limited
range of values of x. To find this range, we impose the ratio test on the terms
of the series. This yields
r(x) ≡ lim
k→∞
f
k+1
(x)
f
k
(x)
< 1, (9.13)
which is an inequality in x that can be solved to find the values of x for which
the series converges.
Example 9.4.1.
As an example of the application of Equation (9.13), let us find
the values of x for which the series
∞
k=1
[ln(x +1)]
k
k
