Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

276 Inﬁnite Series

converges. The ratio in (9.13) is

r(x) = lim

k→∞



[ln(x +1)]

k+1

/(k +1)

[ln(x +1)]



= lim

k→∞



[ln(x +1)]

k+1

[ln(x +1)]

k +1



= |ln(x +1)| lim

k→∞



k +1



= |ln(x +1)|.

So, the condition for convergence is

|ln(x +1)| < 1 ⇒−1 < ln(x +1)< 1

−1

<x+1<e ⇒ e

−1

− 1 <x<e− 1

and the series converges for −0.632 <x<1.718.

Let us now check the convergence of the series for the two end points. The left

end point corresponds to ln(x+1) = −1 for which the series becomes



∞

n=1

(−1)

which is convergent (see Example 9.3.5). On the other hand, for the right end point,

ln(x + 1) = 1, and the series becomes



∞

n=1

1/n which is the divergent harmonic

series. Thus, the interval of convergence is −0.632 ≤ x<1.718.



An important notion is uniform convergence:uniform

convergence

Box 9.4.1. If, for a given , it is possible to ﬁnd an N such that |S

(x)−

S(x)| <whenever n>N for all values of x in some interval (a, b)—so

that N is independent of x—then the series is said to converge uniformly

on (a, b).

Clearly, for uniform convergence to have any meaning, there must exist a range

of values of x for which the series converges uniformly because a series may

converge for all values of x on the real line without converging uniformly for

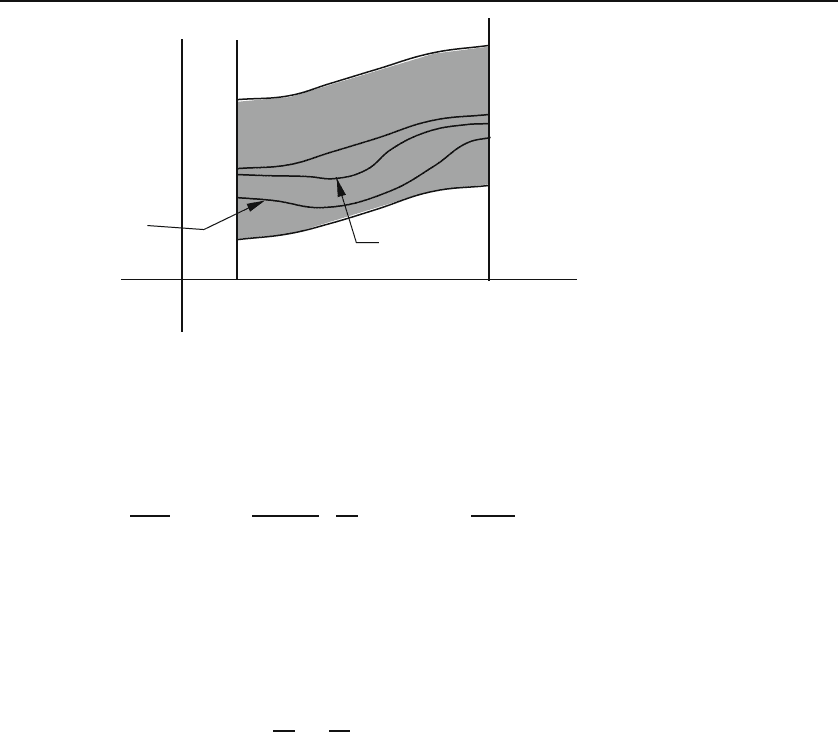
any interval of the real line. A pictorial representation of uniform convergence

is shown in Figure 9.3. Basically, we say that a series is uniformly convergent

if the graphs of partial sums S

(x), after a certain large N , all lie within a

(narrow) strip of width  containing the graph of the limit function f(x).

There is a useful test for the uniform convergence which works for a large

test for uniform

convergence

number of familiar series and goes by the name of the Weierstrass M-test:

Let



∞

k=1

(x) be a series of functions all deﬁned in an interval

(a, b). If

there is a convergent series of positive numbers



∞

k=1

, such that |f

(x)|≤

for all x in (a, b), then



∞

k=1

(x) converges absolutely for each such x,

and is uniformly convergent in (a, b).

Example 9.4.2.

Consider the series



∞

n=1

, which is a generalization of the

geometric series (for which p = 0). We want to see for what values of p and in what

Instead of an interval, one may use the union of many intervals. In fact, the statement

is true even when the interval (a, b) is replaced with a general subset of the real line.

9.4 Sequences and Series of Functions 277

f(x) + ε

f(x) − ε

f(x)

(x)

n+1

(x)

Figure 9.3: Uniform convergence.

interval of x is the series convergent. One way to get the answer is to apply the

ratio test:

lim

n→∞



n+1



= lim

n→∞



n+1

(n +1)



= |x| lim

n→∞



n +1



= |x|.

It follows that, regardless of the value of p, the series converges for |x| < 1, and

diverges for |x| > 1. For x = 1, the series becomes



∞

n=1

1/n

which converges for

p>1 and diverges for p ≤ 1 as pointed out in the integral test of convergence.

Finally if x = −1, the alternating series test of convergence tells us that the series

converges for all p>0. What about the uniformity of convergence? We note that

for M

=1/n

,andfor|x|≤1, we have



≤

≡ M

and the series of M

converges as long as p>1. Thus, for p>1, the series



∞

n=1

is uniformly convergent.



9.4.1 Properties of Uniformly Convergent Series

The importance of uniformly convergent series lies in the nice properties such

series possess. For instance, if u

(x) is continuous in the interval a ≤ x ≤ b,

and if the series



∞

i=1

(x)isuniformly convergent in that interval, then the

function deﬁned by f (x)=



∞

i=1

(x) is also continuous in the interval. This

statement is equivalent to saying that for x and x

in the interval (a, b), one

has

lim

x→x

lim

n→∞

(x)

= lim

n→∞



lim

x→x

(x)



Accordingly, uniform convergence permits the interchange of the two limit

processes.

278 Inﬁnite Series

Another property, which is extremely useful in physical applications, is the

fact that

you can integrate

a uniformly

convergent series

term by term.

Theorem 9.4.3. If f(x)=



∞

i=1

(x) is uniformly convergent, and each

(x) is continuous for a ≤ x ≤ b, then the series can be integrated term by

term, i.e.,

f(x) dx =



∞



i=1

(x)



dx =

∞



i=1

(x) dx,

i.e., integration and summation can be interchanged.

Example 9.4.4.

Consider the geometric series

1−t



∞

i=0

,which,byExample

9.4.2, converges uniformly for −1 <t<1. Changing t to −t does not change either

the interval or the nature of convergence of the series. We thus have

1+t

∞



i=0

(−t)

∞



i=0

(−1)

. (9.14)

Because of the uniform convergence of the series, we can integrate both sides from

0tox with −1 <x<1toobtain

1+t

=ln(1+x)=

∞



i=0

(−1)

dt =

∞



i=0

(−1)

i+1

i +1

With x = 1, we obtain the result alluded to in Example 9.3.5.

Note that the integral of a series may be convergent for a bigger range of values

of its argument than the original series. Here, the original series was divergent (for

t = 1) while its integral converges (for x =1).



The property stated in Theorem 9.4.3 is a useful tool for the expansion

of physical quantities in terms of some more “elementary” quantities. For

example, one can expand the electric potential—usually given in terms of an

integral—as a sum of the potentials of a single charge, a dipole, a quadrupole,

etc. (see Section 10.5). In many physical situations only the ﬁrst few terms

of the series expansion will be of importance. Thus, for instance, in atomic

transitions, it is only the dipole term that participates signiﬁcantly.

One can also diﬀerentiate a uniformly convergent series. To be speciﬁc,

you can

diﬀerentiate a

uniformly

convergent series

term by term.

Theorem 9.4.5. Suppose that u



(x)=du

/dx is continuous for a ≤ x ≤ b,

that the series



∞

n=1

(x) converges to f(x) for a ≤ x ≤ b, and that the

series



∞

n=1



(x) converges uniformly for a ≤ x ≤ b.Then



(x)=

∞



n=1

(x)=

∞



n=1



(x),a≤ x ≤ b,

i.e., one can change the order of diﬀerentiation and summation.

9.5 Problems 279

Other operations deﬁned on uniformly convergent series are addition, sub-

traction, and multiplication by a continuous function: If



∞

i=1

(x)and



∞

i=1

(x) are uniformly convergent for a ≤ x ≤ b and h(x) is continuous

in the same interval, then the series

∞



i=1

(x) ±v

(x)] ,

∞



i=1

h(x)u

(x),

are also uniformly convergent for a ≤ x ≤ b.

Historical Notes

The mathematicians of the seventeenth and eighteenth centuries used series indis-

criminately. By the beginning of the nineteenth century some absurd results from

manipulating inﬁnite series stirred up some interest in questioning the validity of

operations performed on them. Around 1810 a number of mathematicians began

the exact handling of inﬁnite series.

In his 1811 paper and his Analytical Theory of Heat, Fourier gave a satisfactory

deﬁnition of convergence, though in general he worked freely with divergent series.

His deﬁnition of convergence was essentially in terms of the sequence of partial sums.

Moreover, he recognized that the convergence of a series of functions of the variable

x maybeachievedonlyinanintervalofx values. Although Fourier stressed that

a necessary condition for convergence is that the terms of the series approach zero,

he was fooled by the series



∞

k=0

(−1)

, and thought that its sum was

[substitute

t = 1 on both sides of (9.14)].

The ﬁrst important and strictly rigorous investigation of convergence was made

by Gauss in his 1812 paper Disquisitiones Generales Circa Seriem Inﬁnitam wherein

he studied the hypergeometric series (see Section 11.2.1). Though Gauss is often

mentioned as one of the ﬁrst to recognize the need for restricting the series to their

interval of convergence, he avoided any decisive position. He was so much concerned

to solve concrete problems by numerical calculations that he used a divergent ex-

pansion of the gamma function. When he did investigate the convergence of the

hypergeometric series, he remarked that he did so to please those who favored the

rigor of the ancient geometers.

Cauchy’s work on the convergence of series is the ﬁrst extensive treatment of

the subject. In his Cours d´Analyse Cauchy clearly deﬁnes the sequence of partial

sums and gives a rigorous deﬁnition of the convergence and divergence of the series

in terms of this sequence. It is also in this work that he gives what is now called

the Cauchy criterion for convergence of a sequence (see Box 9.1.1). He proves this

to be a necessary condition, but merely remarks that if the condition holds, the

convergence of the series is assured. He lacked the knowledge of the properties of

real numbers to provide a proof. Cauchy then goes on to state and prove many of

the results that we have outlined in our discussion of the tests for convergence.

9.5 Problems

9.1. Show that

(a)



k=1

k−1



n−1

k=0

(k +1)z

. (b) x



k=0



n+2

k=2

k−2

280 Inﬁnite Series

9.2. Use some small values of M and N (say M =2,N =3)andverifythe

validity of Equation (9.6).

9.3. Use Equation (9.8) to show that



m +1









k − 1



9.4. Use mathematical induction to prove the following relations:

(a)

)=nx

n−1

. (b)



k=0

n+1

−1

x−1

9.5. Use the integral test to show that the harmonic series of order p is

convergent for p>1 and divergent for p ≤ 1.

9.6. Test the following series for convergence or divergence:

(a)



∞

n=1

(−1)

. (b)



∞

n=1

(−1)

sin

nα

n+1

. (c)



∞

n=1

ln n

(d)



∞

n=1

n+1

+3n

. (e)



∞

n=1

n+1

+5n−10

. (f)



∞

n=2

n ln n

where α is some real number. For (c), consider the three cases p>1, p<1,

and p =1.

9.7. Prove convergence or divergence by the comparison test:

∞



n=1

sin n

∞



n=2

− 1

∞



n=1

n +5

− 3n − 5

∞



n=2

√

n ln n

9.8. Prove convergence or divergence by the integral test:

∞



n=1

∞



n=1

∞



n=2

n ln

∞



n=2

n ln n ln ln n

9.9. Prove convergence or divergence by the ratio test:

∞



n=1

+ n

∞



n=1

(−1)

∞



n=1

9.10. Use the ratio test to ﬁnd the range of values of x for which the following

series converge. Make sure to investigate the end points.

(a)



∞

n=1

(ln x)

n+1

. (b)



∞

n=1

sin

(n+1)5

(c)



∞

n=1

√

(d)



∞

n=1

(ln x)

. (e)



∞

n=1

. (f)



∞

n=3

(x−2)

(g)



∞

n=1

. (h)



∞

n=1

n!x

. (i)



∞

n=1

(ln x)

(j)



∞

n=0

. (k)



∞

n=1

+1)

. (l)



∞

n=1

(x+1)

(m)



∞

n=0





. (n)



∞

n=1



√



. (o)



∞

n=0

(x−2)

(p)



∞

n=0

. (q)



∞

n=1

. (r)



∞

n=0

.[6bp]

9.5 Problems 281

9.11. Write the ﬁrst four terms of the following series:

∞



n=1

2 · 4 ···2n

∞



n=1

(−1)

ln(n +1)

∞



n=1

√

∞



n=1

√

Test for convergence or divergence of these series.

Chapter 10

Application of Common

Series

The preceding chapter concerned itself with the formal properties of inﬁnite

sequences and series, especially the sequences and series of functions. One

of the useful properties of the inﬁnite series of functions is that they can be

approximated by ﬁnite sums. In this approximation, two important features

of the series play crucial roles: the simplicity of the functions used in the series

and the convergence of the series. This chapter deals with some of the series

of functions most commonly used in mathematical physics.

10.1 Power Series

One of the most common series of functions is the power series where the

nth term of the series is c

(x − a)

with c

a real number. To be speciﬁc, a

power series in powers of (x −a)isoftheform

∞



n=0

(x −a)

= c

+ c

(x −a)+c

(x −a)

+ ··· . (10.1)

An important special case is when a =0,sothatwehave

∞



n=0

= c

+ c

x + c

+ ··· . (10.2)

Sometimes negative powers are also included, but by power series we usually

mean Equation (10.1).

We note that Equation (10.1) converges for x = a. The question is whether

radius of

convergence of a

power series

it converges for any other values of x, and if so, what these values are. It turns

out that:

284 Application of Common Series

Theorem 10.1.1. Every power series



∞

n=0

(x − a)

has a radius of

convergence r

∗

such that the series converges absolutely and uniformly when

|x − a| <r

∗

and diverges for |x −a| >r

∗

.Ifr

∗

=0and r

is a number such

that 0 <r

∗

, then the series converges absolutely and uniformly for

|x − a|≤r

The number r

∗

can be 0 (in which case the series converges only for x = a),

a ﬁnite positive number, or ∞ (in which case the series converges for all x).

The radius of convergence can be evaluated by using the ratio test. Con-

sider the ratio

r(x) = lim

n→∞



n+1

(x − a)

n+1

(x − a)



= |x − a| lim

n→∞



n+1



and note that the series converges if r(x) < 1, or

|x − a| < lim

n→∞



n+1



The RHS is naturally deﬁned to be the radius of convergence

∗

= lim

n→∞



n+1



if the limit exists. (10.3)

It can be shown that the radius of convergence can also be found from the

following formula:

∗

= lim

n→∞



if the limit exists. (10.4)

Example 10.1.2.

Consider the exponential function e

which, as we shall see,

has a power series expansion

≡

∞



n=0

∞



n=0

By the ratio test, we have

r(x) = lim

n→∞



n+1

/(n +1)!

/n!



= lim

n→∞

|x|



(n +1)!



= |x| lim

n→∞



n +1



for all values of x. So, regardless of x, the series representation of e

converges, i.e.,

the radius of convergence is inﬁnite. We can also use Equation (10.3) to calculate

the radius of convergence

∗

= lim

n→∞



n+1



= lim

n→∞



1/n!

1/(n +1)!



= lim

n→∞

|n +1| = ∞.



Example 10.1.3. Let us ﬁnd the interval of convergence of

∞



k=0

(−1)

(k +1)

10.1 Power Series 285

The ratio test gives

r(x) = lim

k→∞



k+1

(x)



= lim

k→∞



(−1)

k+1

/[4

k+1

(k +2)]

(−1)

/[4

(k +1)]



= lim

k→∞



x(k +1)

4(k +2)



lim

k→∞



k +1

k +2





 

|x|

So, the series converges if r(x) < 1, i.e., if |x| < 4, or −4 <x<4.

What about the end points? For x = 4, the series becomes

∞



k=0

(−1)

k +1

which is the alternating series and it converges. On the other hand, if x = −4, the

series becomes

∞



k=0

(−1)

(−4)

(k +1)

∞



k=0

(−1)

k +1

∞



k=0

k +1

which is the divergent harmonic series. So, the interval of convergence of the series

is −4 <x≤ 4, and its radius of convergence is r

∗

=4.



Because of the uniform convergence of power series, we can perform all

the common operations used for ordinary functions on the power series. We

list all these properties in the following:

 Continuity. A power series represents a continuous function within its

a convergent

power series

represents a

continuous

function

radius of convergence; i.e., if r

∗

is the radius of convergence, then the

series

f(x)=

∞



n=0

(x −a)

for a −r

∗

<x<a+ r

∗

(10.5)

is continuous.

 Integration. The power series (10.5) can be integrated term by term

aconvergent

power series can

be integrated term

by term

within its radius of convergence; i.e., for a − r

∗

<p<q<a+ r

∗

f(t) dt =

∞



n=0

(t −a)

dt =

∞



n=0

(q − a)

n+1

− (p −a)

n+1

n +1

(10.6)

 Diﬀerentiation. The power series (10.5) can be diﬀerentiated term by

a convergent

power series can

be diﬀerentiated

term by term

term within its radius of convergence; that is,



(x)=

∞



n=1

(x − a)

n−1

,a− r

∗

<x<a+ r

∗

. (10.7)

 Zero Power Series. If a power series has nonzero radius of convergence

if two power series

are equal, so are

their correspond-

ing coeﬃcients

and has a sum which is identically zero, then every coeﬃcient of the

series must be zero. This leads to the following

286 Application of Common Series

Theorem 10.1.4. If two power series



∞

n=0

(x − a)

and



∞

n=0

(x − a)

have nonzero convergence radii and have equal sums whenever

both series converge, then the two series are identical, i.e.,

= b

,n=0, 1, 2,....

This property is very eﬀectively used to ﬁnd solutions of diﬀerential

equations in terms of inﬁnite power series.

10.1.1 Taylor Series

A power series whose coeﬃcients are derivatives of the function representing

the sum is called Taylor series . More precisely, let

f(x)=

∞



n=0

(x − a)

,a− r

∗

<x<a+ r

∗

. (10.8)

This series is called the Taylor series of f(x)atx = a if the coeﬃcients c

are

given by the rule:

= f (a),c



(a)



(a)

,..., c

(k)

(a)

so that

Taylor series

f(x)=f(a)+



(a)

(x − a)+···+

(k)

(a)

(x −a)

+ ···

∞



k=0

(k)

(a)

(x − a)

where f

(0)

(a) ≡ f(a), 0! ≡ 1. (10.9)

From Theorem 10.1.4 and the equality of (10.8) and (10.9), we conclude that

every power series with nonzero convergence radius is the Taylor series of the

function denoting its sum, and conversely every inﬁnitely diﬀerentiable func-

tion can be represented by a Taylor series within the interval of convergence

of the series.

An alternative way of writing the Taylor series which suggests approxima-

tion is to let Δx = x −a. Then Equation (10.9) becomes

Taylor series and

approximating

functions

f(a +Δx)=f(a)+



(a)

Δx + ···=

∞



k=0

(k)

(a)

(Δx)

Since a is an arbitrary real number, we can replace it with x which is more

suggestive of the generality of this formula:

f(x +Δx)=f(x)+



(x)

Δx + ···=

∞



k=0

(k)

(x)

(Δx)

. (10.10)

With Δx interpreted as the increment in x, Equation (10.10) states that the

function at the incremented value of x is f(x) plus a “correction” involving