Hatano Y., Katsumura Y., Mozumder A. (Eds.) Charged Particle and Photon Interactions with Matter - Recent Advances, Applications, and Interfaces

Подождите немного. Документ загружается.

370 Charged Particle and Photon Interactions with Matter

Finally, we should note that, in the time domain beyond a few microseconds, the reactions that

occur in the bulk solution can usually be well described with conventional homogeneous chemistry

methods

(Pastina and LaVerne, 1999).

14.4.3 controverSial iSSueS: priMary yieldS of

HO O

2 2

i i

and h

verSuS let

andthe production of o

in the heavy-ion radiolySiS of water at high let

Under heavy-ion irradiation conditions, the general trends on increasing LET of the radiation are

to give lower free-radical and higher molecular primary yields (e.g., Allen, 1961; Anderson and

Hart, 1961; Pucheault, 1961; Burns and Sims, 1981; Appleby, 1989; Elliot et al., 1996; McCracken

et al., 1998; Ferradini and Jay-Gerin, 1999; LaVerne, 2000a, 2004). This behavior is explained by

the increased intervention of radical–radical reactions as the local concentration of radicals along

the track of the impacting ion is high and many radical interactions occur before the products can

escape into the bulk solution. This should permit fewer radicals to escape combination and recom-

bination reactions during the expansion of the tracks and in turn lead to the formation of more

molecular

products. However, there are two important exceptions to this rule:

1. Unlike the behavior of other radicals, the primary yield of the superoxide anion radical

i−

and its conjugate acid

(hydroperoxyl radical) (

i−

is always in a pH-dependent equi-

librium with

, pK

= 4.8; see: Bielski et al., 1985) rises sharply with LET (Donaldson

and Miller, 1956; Lefort and Tarrago, 1959; Appleby and Schwarz, 1969; Bibler, 1975;

Baverstock and Burns, 1976; Sims, 1978; Burns and Sims, 1981; LaVerne et al., 1986;

LaVerne and Schuler, 1987b; Baldacchino et al., 1998a,b; McCracken et al., 1998; Wasselin-

Trupin et al., 2000). As mentioned earlier, with fast electrons and γ-rays, the production of

HO /O

2 2

i i−

is normally neglected because its very small yield of ∼0.02 molecule/100eV

accounts for less than 1% of the other primary radiolytic species. However, with high-LET

heavy ions, it is the major radical product that survives spur/track expansion, since the other

primary radical G-values, i.e., those of

•

OH, H

•

, and

−

, are virtually zero. The origin of

these

HO /O

2 2

i i−

radicals is, as yet, not clearly established, even though there are a number

of suggested (but not completely adequate) mechanisms to account for their formation and

their increase with increasing LET (for reviews, see Sims, 1978; LaVerne, 1989; Ferradini

and Jay-Gerin, 1998).

2. A second peculiar feature is that the primary yield of H

rises with increasing LET to

a maximum, after which it falls (Sims, 1978; Burns and Sims, 1981; Pastina and LaVerne,

1999; Wasselin-Trupin et al., 2002). It has been shown that the maximum in the value of

H O

2 2

occurs precisely at the point where

HO /O

2 2

i i−

begins to rise sharply, suggesting that the

yields of

HO /O

2 2

i i−

and H

are closely linked (Sims, 1978). Apart from calculations using

the Schwarz diffusion model (Schwarz, 1969; Burns and Sims, 1981), which predict a slight

maximum in the H

yield, but at lower LET than is found experimentally,* there is hitherto

no suitable explanation for the presence of such a maximum in

H O

2 2

as a functionof LET.

Another controversial issue in the radiolysis of water at high LET concerns the hypothesis of

the generation of O

in heavy-ion tracks. Oxygen is a powerful radiation sensitizer; the biological

response to irradiation is greater under oxygenated conditions than under hypoxic conditions (e.g.,

Hall and Giaccia, 2006; von Sonntag, 2006). This ability of oxygen to sensitize cells to damage from

ionizing radiation has been known for many years.

†

The degree of sensitization can be quantied by

* In addition, the Schwarz model cannot account for the

HO /O

i i−

yield at high LET, suggesting that, at high LET, addi-

tional

mechanisms, which are not included in the model, become important.

†

For an account of the historical development of the subject, see, e.g., Gray et al., 1953; Patt, 1953; Howard-Flanders,

1958.

Radiation Chemistry of Liquid Water with Heavy Ions: Monte Carlo Simulation Studies 371

the “oxygen enhancement ratio” (OER), the ratio of the dose without oxygen to the dose with oxygen

needed to achieve the same biological effect. The OER is recognized as a dose-modifying factor

of fundamental importance in radiobiology as well as of practical relevance in radiotherapy (since

many tumors contain high levels of hypoxia). For low-LET radiations with conventional dose rates,

the OER values are generally found between 2 and 3. For most cellular organisms, the oxygen effect

shows a strong dependence on radiation quality; the OER decreases progressively with increasing

LET of the radiation used, approaching its minimum value of 1 when the LET becomes greater

than 100–200 keV/μm (e.g., Barendsen, 1968; Alper and Bryant, 1974). In other words, for high-

LET radiation, the survival of tumor cells is practically the same in the presence or in the absence

of O

(Curtis et al., 1982). To account for this experimental nding, Scholes and Weiss (1959),

Swallow and Velandia (1962), Neary (1965), and Alper and Bryant (1974) invoked the “oxygen-

in-the-track” hypothesis, suggesting that O

generated in the tracks of densely ionizing particles,

as they traverse the biological material, is responsible for the decrease of OER with LET. In other

words, cells exposed to high-LET radiation exhibit an “oxygenated” microenvironment around the

particle track, even when they are irradiated under anoxic (i.e., no oxygen) conditions (Baverstock

and Burns, 1976, 1981). This hypothesis of the generation of molecular oxygen in heavy-ion tracks,

which presupposes that O

is a product of the radiolysis of water at high LET (for radiation of low

LET, O

is not a radiolytic product), has often been invoked for a variety of aqueous biological

systems, but other mechanisms have also been considered to explain the observed decrease in the

OER with LET (see below), and a denite conclusion supporting this hypothesis has not yet been

forthcoming.

14.4.4 hypotheSiS of Multiple ionization of waterinSinglecolliSionS

under heavy-ion boMbardMent

When an impacting heavy-charged particle (particularly a multiply charged heavy ion) collides

violently with a multielectron target molecule, some of the translational kinetic energy of the ion is

deposited in the electronic degrees of freedom of the target, with the result that the target emerges

with an electronic excitation or ionization. Collisions at sufciently large impact parameters will

produce only singly ionized and excited molecules. As the impact parameter becomes smaller,

multiple ionization (MI) of the target’s outer (loosely bound) electron shells in a “single act” occurs

with appreciable probabilities. For small impact parameters, inner-shell electrons can be ejected

along with the multiple ionization of the outer shells (for reviews, see Cocke and Olson, 1991;

McDaniel et al., 1993; ICRU Report 55, 1996; Toburen, 2004). Although inner-shell ionization

(followed by Auger relaxation) effects are well known,* the consequences of direct multiple outer-

shell ionization with two (or more) outgoing electrons in the nal state have not often been consid-

ered in the models of radiation chemistry and biology. In fact, more than 50 years ago, Platzman

(1952) concluded, in a discussion of the possible role of direct, multiple target ionization in radia-

tion action, that these processes, although infrequent relative to single ionization events, should be

“extremely effective chemically” owing to the high instability of the multiply ionized molecules

produced.

†

In this same radiation–chemical context, the hypothesis of “multiple ionization of a

* Creation of an initial inner-shell vacancy (hole) by a swift charged particle is followed by the emission of one (or several)

Auger electrons (commonly called an Auger cascade) in the ensuing “rearrangement” of the electron cloud as the excited

atom/molecule relaxes to the ground state. Typically, the energy transferred in such a process amounts to some hundreds

of electronvolts (i.e , the K-shell ionization energies of a C, N, and O atom are 283.8, 401.6, and 532eV, respectively).

Auger

relaxation can produce doubly (or multiply) charged target ions (e.g., Chattorji, 1976).

†

Platzman (1952) also pointed out the possibility of formation, by the incident particle, of multiply “excited” atoms or

molecules in single collisions. By multiple excitation is meant the simultaneous excitation, by a passing charged particle,

of several electrons in a single atom or in atoms closely coupled together in a molecule. According to this author, this

process should be less likely to have a signicant inuence on chemical or biological effects than does multiple ioniza-

tion.

Multiple excitation is ignored in the present work.

372 Charged Particle and Photon Interactions with Matter

single molecule or of near neighbors” was also proposed by Gäumann and Schuler (1961) as a pos-

sible explanation for the large increase in the yield of H

in the radiolysis of benzene by densely

ionizing radiations (relative to that produced by fast electrons). Recently, Ferradini and Jay-Gerin

(1998) reconsidered this earlier hypothesis and suggested that MI could play a signicant role in

the heavy-ion radiolysis of liquid water at high LET. In particular, they proposed that MI could

intervene to explain the large yields of

HO /O

2 2

i i−

observed experimentally in high-LET water

radiolysis (see above).

Multiple ionization has long been recognized as an important process in atomic physics, and

experimental data have accumulated for many years. Most experiments have been performed with

light ions in the gas phase. The importance of the direct outer-shell ionization in fast ion–atom

collisions was rst clearly demonstrated by the measurements of Manson et al. (1983), who stud-

ied 0.5–4 MeV protons incident on neon. They showed, at least for that target, that direct double

ionization was the dominant Ne

production process, far more probable than inner-shell ioniza-

tion (the Auger channel). In fact, inner-shell ionization cross sections are generally several orders

of magnitude smaller than direct outer-shell ionization, that is, inner-shell ionization is a “rare”

event (Toburen, 2004). The multiple ionization and the possible avenues of fragmentation (fol-

lowing MI) of polyatomic molecular targets induced by the interaction with heavy ions have been

investigated intensively only recently. For water vapor, experimental studies have been reported

so far by several groups (e.g., Werner et al., 1995a,b; Olivera et al., 1998; Siegmann et al., 2001;

Pešic´ et al., 2004; Legendre et al., 2005; Montenegro and Luna, 2005; Alvarado et al., 2005;

Alvarado, 2007; for a recent review, see Stolterfoht et al., 2007). Specically, it is found that the

cross section for double ionization is usually more than an order of magnitude less than for single

ionization. Triple ionization is usually more than an order of magnitude less than double ioniza-

tion. The similar ionization of higher multiplicity is much less probable (e.g., LaVerne, 2000a;

Champion, 2003; Champion et al., 2005; Gervais et al., 2005, 2006). For such collisions, the

double-, triple-, and quadruple ionization thresholds for H

O are ∼40, 65, and 88eV, respectively

(Meesungnoen and Jay-Gerin, 2005a). To our best knowledge, only limited data exist for studies

of MI under highly charged ion impact for molecular systems of chemical or biological impor-

tance in the “condensed” phase. This is explained by the fact that such experiments are extremely

difcult and further complicated by the occurrence of many possible molecular break-up chan-

nels following ionization. Theoretically, a detailed description of MI is also a difcult task due

to the complex, quantum-mechanical many-body nature of the scattering mechanisms involved.

Nevertheless, a few attempts have been made recently to simulate the role of multiple ionization

in liquid water with the aim of evaluating its consequences in the heavy-ion radiation chemistry

of water (Meesungnoen et al., 2003; Meesungnoen and Jay-Gerin, 2005a,b, 2009; Gervais et al.,

2005, 2006; Gaigeot et al., 2007).

14.5 monte Carlo simulations oF high-let water radiolysis

The complex sequence of events that follow absorption in liquid water of ionizing radiation can be

modeled successfully by the use of Monte Carlo simulation techniques. Such a procedure is well

adapted to account for the stochastic nature of the phenomena, provided that realistic probabili-

ties and cross sections for all possible events are adequately known. The simulation then allows

one to reconstruct the intricate action of the radiation. It also offers a powerful tool for apprais-

ing the validity of different assumptions, for making a critical examination of proposed reaction

mechanisms, and for estimating some unknown parameters. The accuracy of these calculations

is best determined by comparing their predictions with experimental data on well-characterized

chemical systems that have been examined with a wide variety of incident radiation particles and

energies.

Turner and his collaborators at the Oak Ridge National Laboratory (Oak Ridge, Tennessee)

jointly with Magee and Chatterjee at Lawrence Berkeley Laboratory (Berkeley, California) were

Radiation Chemistry of Liquid Water with Heavy Ions: Monte Carlo Simulation Studies 373

the rst to use Monte Carlo simulations to derive computer-plot representations of the chemical evo-

lution of a few keV electron tracks in liquid water at times between ∼10

−12

and 10

−7

s (Turner et al.,

1981, 1983, 1988). Following this pioneering work, stochastic simulation codes employing Monte

Carlo procedures were used with success by a number of investigators to study the relationship

between the initial track structure and the ensuing chemical processes that occur in the radiolysis

of both pure water and water-containing solutes (for reviews, see, e.g., Ballarini et al., 2000; Uehara

and Nikjoo, 2006; Kreipl et al., 2009). Two main approaches have been widely used: (1) the “step-

by-step” (or random ights Monte Carlo simulation) method, in which the trajectories of the dif-

fusing species of the system are modeled by time-discretized random ights and in which reaction

occurs when reactants undergo pairwise encounters, and (2) the “independent reaction times” (IRT)

method (Clifford et al., 1986; Pimblott et al., 1991; Pimblott and Green, 1995), which allows the cal-

culation of reaction times without having to follow the trajectories of the diffusing species. Among

the stochastic approaches, the most reliable is certainly the full random ights simulation, which

is generally considered as a measure of reality. However, this method can be exceedingly consum-

ing in computer time when large systems (such as complete radiation tracks or track segments) are

studied. The IRT method was devised to achieve much faster realizations than are possible with the

full Monte Carlo model. In essence, it relies on the approximation that the distances between pairs

of reactants evolve independently of each other, and, therefore, the reaction times of the various

potentially reactive pairs are independent of the presence of other reactants in the system. For every

pair, a reaction time is stochastically sampled according to the time-dependent survival function

(Green et al., 1990; Goulet and Jay-Gerin, 1992; Frongillo et al., 1998) that is appropriate for the

type of reaction considered. This function depends on the initial (or zero-time) distance separating

the species, their diffusion coefcients, their Coulomb interaction, their reaction radius, and the

probability of reaction during one of their encounters. The rst reaction time is found by taking

the minimum of the resulting ensemble of reaction times and allowing the corresponding pair of

species to react at this time. This procedure for modeling reaction is continued either until all reac-

tions are completed or until a predened cut-off time is reached. The IRT simulation technique also

allows one to incorporate, in a simple way, pseudo rst-order reactions of the radiolytic products

with various scavengers that are homogeneously distributed in the medium (such as H

, OH

−

, and

O itself, or more generally any solutes for which the relevant reaction rates are known). The abil-

ity of the IRT method to give accurate time-dependent chemical yields has been well validated by

comparison with full random ight Monte Carlo simulations that do follow the reactant trajectories

detail (Pimblott et al., 1991; Goulet et al., 1998; Plante, 2009).

14.5.1 the ionlyS-irt SiMulation code

In a program begun in the summer of 1988 in collaboration with Jean Paul Patau (Université Paul-

Sabatier, Toulouse, France) and Christiane Ferradini (Université René-Descartes, Paris, France), the

Sherbrooke group has developed and progressively rened, with very high levels of detail, several

Monte Carlo codes that simulate the track structure of ionizing particles in water, the production of

the various ionized and excited species, and the subsequent reactions of these species in time with

one another or with available solutes (Cobut, 1993; Cobut et al., 1998; Frongillo et al., 1998; Hervé

du Penhoat et al., 2000; Meesungnoen et al., 2001, 2003; Meesungnoen and Jay-Gerin, 2005a,b,

2009; Muroya et al., 2002, 2006; Plante et al., 2005; Autsavapromporn et al., 2007; Guzonas et al.,

2009). A most recent version of the Sherbrooke codes, called IONLYS-IRT (Meesungnoen and Jay-

Gerin,

2005a,b), is used in the present work.

Briey,

the IONLYS step-by-step simulation program models all the events of the physical

and physicochemical stages in the track development. To take into account the effects of multiple

ionizations under high-LET heavy-ion impact, the model incorporates double-, triple-, and qua-

druple ionization processes in single ion–water collisions (see above). The double ionization of

water is assumed to lead to the production of

HO /O

2 2

i i−

through the intervention of oxygen atoms

374 Charged Particle and Photon Interactions with Matter

(Kuppermann, 1967; LaVerne et al., 1986; Gardès-Albert et al., 1996; Olivera et al., 1998) formed in

their

P ground state (Ferradini and Jay-Gerin, 1998), according to*

H O H O H O O

2 2 3

2 2

++ +

+ → + ( )P (14.19)

very short times, followed by

i i

OH O HO

+ →( )

P (14.20)

As for the triple and quadruple ionizations of water molecules, they are assumed to lead directly to

the formation of

HO /O

2 2

i i−

and O

, respectively, by acid–base re-equilibration reactions, according

(Ferradini and Jay-Gerin, 1998; Meesungnoen and Jay-Gerin, 2005a)

H O H O 3H O HO

2 3

i i+

+ → + (14.21)

and

H O H O 4H O O

2 3 2

+ → + . (14.22)

The complex spatial distribution of reactants at the end of the physicochemical stage, which is pro-

vided as an output of this program, is used directly as the starting point for the nonhomogeneous

chemical stage. This third and nal stage is covered by the program IRT, which employs the IRT

method to model the chemical development that occurs during this stage and to simulate the for-

mation of the measurable yields of chemical products. Its detailed implementation has been given

previously (Frongillo et al., 1998). Only slight adjustments have been made in some reaction rate

constants and the diffusion coefcients of reactive species to take account of the latest data available

from the literature. The reaction scheme used in our IRT program for pure liquid water is given in

Table

14.1.

simulate the radiolysis of (deaerated) water under acidic conditions with IONLYS-IRT, we have

used 0.4 M H

aqueous solutions

†

and supplemented the pure-water reaction scheme to include

the seven reactions listed in Table 14.2, which account for the species present in irradiated sulfu-

ric acid solutions. The details of our computational modeling are given elsewhere (Meesungnoen

et al., 2001; Meesungnoen and Jay-Gerin, 2005b; Autsavapromporn et al., 2007). To summarize,

the effects of the background concentrations of H

in solutions were added to the IRT program as

pseudo rst-order reactions. In addition, we have introduced the effects due to the ionic strength of

the solutions for all reactions between ions, except for the peculiar bimolecular self-recombination

−

for which there is no evidence of any ionic strength effect (Schmidt and Bartels, 1995). The

rate constants for those various reactions, corrected for these ionic strength effects, were used in the

* A fragmentation mechanism, based on the “Coulomb explosion” of multiply ionized water molecules observed in the gas

phase, has also been proposed recently to explain the formation of

HO /O

2 2

i i−

and O

in the heavy-ion radiolysis of liquid

water

at high LET (Gervais et al., 2005, 2006; Gaigeot et al., 2007). This mechanism is discussed below in relation with

reactions

(14.19) through (14.22).

†

At such a high concentration of H

(pH 0.46), the H

ions capture most, if not all, of the hydrated electrons in the

expending

spurs/tracks to form H

•

atoms (e.g., Ferradini and Jay-Gerin, 2000):

H H

− +

+ →

(14.23)

with a bimolecular rate constant of ∼1.12 × 10

−1

(value corrected to take into account ionic strength effects at this

acid

concentration) (Meesungnoen et al , 2001).

Radiation Chemistry of Liquid Water with Heavy Ions: Monte Carlo Simulation Studies 375

calculations. Finally, in our simulations, the direct action of ionizing radiation on the sulfuric acid

anions

(mainly

HSO

−

) has been neglected, which is a reasonably good approximation.*

The inuence of the LET on the yields of the various radiation-induced species produced in

neutral water and in 0.4 M H

aqueous solutions at 25°C was investigated by varying the impact-

ing ion energy from ∼300 to 0.15MeV (∼0.3–70keV/μm) for protons,

†

∼300 to 0.3MeV/nucleon

(∼1.25–213keV/μm) for

, ∼300 to 1.25MeV/nucleon (∼12–604keV/μm) for

, and ∼300 to

3.2MeV/nucleon (∼25–938keV/μm) for

. The calculations were performed by simulating short

(∼1.5–100μm) ion track segments, over which the energy and LET of the ion are well dened and

remain nearly constant. Typically, ∼5,000–400,000 reactive chemical species were generated in

those simulated track segments (depending on ion type and energy), thus ensuring only small sta-

tistical uctuations in the determination of average yields. Finally, at the incident ion energies of

interest here, interactions involving electron capture and loss by the moving ion (charge-changing

collisions) have been neglected (Pimblott and LaVerne, 2002). The nuclear fragmentation of incident

beam

projectiles is also ignored.

14.5.2 Multiple ionization croSS SectionS and the fate

of Multiply ionized water MoleculeS

14.5.2.1 Cross sections for multiple ionization of water molecules

The successful Monte Carlo modeling of heavy-ion radiation effects in water relies on the knowl-

edge of the cross sections of all interaction processes. The multiple ionization of a single water

molecule induced by swift heavy-ion impact has been observed in many circumstances. However,

* In fact, in 0.4 M H

, only ∼3.5% of the total energy expended in the solution is initially absorbed by direct action

HSO

−

(rather than on H

O) (assuming that the energy absorbed by each component is proportional to its electron

fraction).

†

To reproduce the effects of fast electron or

Co γ-radiolysis, we used ∼300 MeV protons whose average LET value

obtained

in the simulations was ∼0.3

keV/μm.

table 14.2

reactions

dded

to the p

ure

ater

eaction

cheme

to s

imulate

the r

adiolysis

eaerated

queous

0.4mh

solutions,

at 25°C

reaction k (m

−1

)

H SO HSO

i i

+ →

− −

1.0 × 10

H S O SO HSO

2 4 4

i i

+ → +

− − −

2.5 × 10

i i

OH HSO H O SO

4 4

+ → +

− −

1.5 × 10

e S O SO S O

− − − −

+ → +

2 8

4 4

1.2 × 10

H O SO HO HSO

2 4 2 42

+ → +

− −i i

1.2 × 10

OH SO OH S O

4 4

− − −

+ → +

i i 2

8.3 × 10

SO SO S O

4 4

i i− − −

+ →

2 8

4.4 × 10

Source: Autsavapromporn, N. et al., Can. J. Chem., 85, 214,

2007.

The rate constants given here for the reactions between

ions

are at ionic strength equal zero.

376 Charged Particle and Photon Interactions with Matter

a survey of the literature shows that most of experiments have been performed with ions in water

vapor but not in liquid water, as measurements with liquid are either impractical or very difcult.

As well, all existing heavy-ion cross section calculations have been performed for water vapor. Due

to this scarcity of reliable “condensed-phase” cross-section data, a quantitative description of MI

effects in liquid water represents a challenging problem. In an effort to overcome these difculties,

we infer here the MI cross sections indirectly from measurements made in the liquid phase. As

described previously (Meesungnoen and Jay-Gerin, 2005a), our strategy mainly consists in treating

the ratio of the double-to-single ionization cross sections (α = σ

/σ

, where σ

, the “single” ion-

ization cross section, is known) in our track simulations as an adjustable parameter chosen to best

t the available experimental values of

( )G G

as a function of LET in the heavy-ion radi-

olysis of air-free aqueous FeSO

(1 mM)–CuSO

(10mM) solutions under acidic (0.005 M H

pH∼2.1) conditions* (LaVerne et al., 1986; LaVerne and Schuler, 1987b; LaVerne, 1989). As for

the triple and quadruple ionizations of water (which are shown, under the conditions of this study,

to contribute only weakly to the production of

HO /O

2 2

i i−

and O

), σ

and σ

are assumed to be

equal to α

and α

(α < 0.5), respectively, in accordance with the calculated ratios of σ

/σ

(where σ

is the cross section for the ejection of j electrons) for collisions of various heavy ions on

gas-phase H

O molecules (Champion, 2003; Champion et al., 2005; Gervais et al., 2005, 2006).

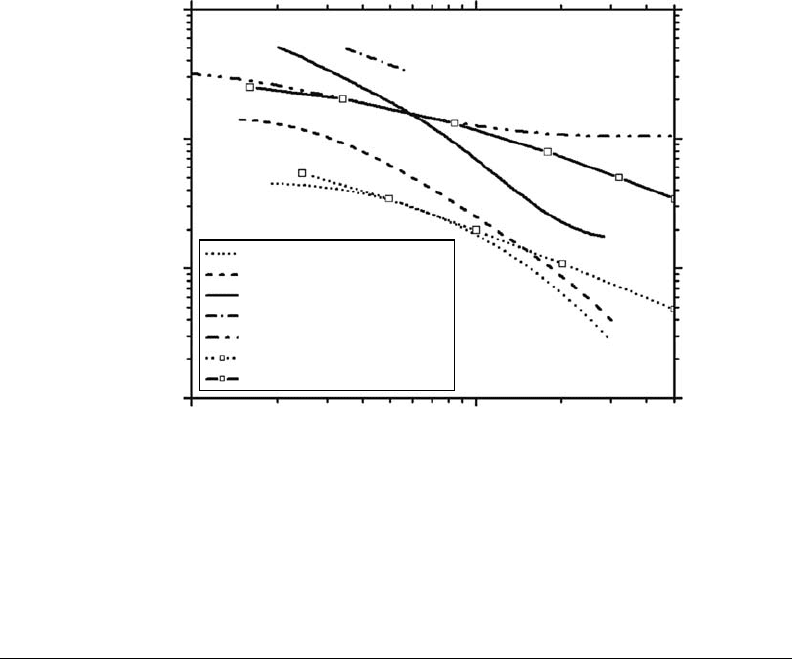
The values of α so obtained are shown in Figure 14.6 for the four impacting ions considered in this

* The principle of this (indirect) method to measure

is to generate molecular oxygen by the reaction of

with

cupric ion (e.g., Hart, 1955; Donaldson and Miller, 1956). It should be noted here that any primary O

, produced directly

or by track reactions, will also be measured using this method. Therefore, the yields generally quoted for

under

these experimental conditions also include O

(Baverstock and Burns, 1976; LaVerne, 2004; Meesungnoen and Jay-

Gerin,

2005a).

–1

–2

–3

0.1 1

ion

/Z (MeV/nucleon)

/σ

Champion(2003)

from Gervais et al.(2006)

from Gervais et al. (2006)

Figure 14.6 Plot of the ratio of double-to-single ionization cross sections (α = σ

/σ

) against E

ion

/Z, where

ion

is the ion energy per nucleon and Z is the projectile charge number. The short-dot, dash, solid, and dash-

dot lines represent, respectively, the α values for

, and

impacting ions, obtained from

our Monte Carlo simulations (see text for explanation). The dash-dot-dot line shows the α values reported by

Champion (2003), and the symbols (□) with dot and solid lines represent the α values calculated by Gervais

et al. (2006) for protons and carbon ions, respectively. (From Meesungnoen, J. and Jay-Gerin, J.-P., J. Phys.

Chem. A,

109, 6406, 2005a. With permission.)

Radiation Chemistry of Liquid Water with Heavy Ions: Monte Carlo Simulation Studies 377

work (namely,

,

, and

) as a function of (E

ion

/Z), the ion energy per nucleon

divided by the projectile charge number. The corresponding σ

/σ

values reported by Champion

(2003) and Gervais et al. (2006) for various ions and gaseous water are also included in the gure

for the sake of comparison. It is seen that our values of α depend on the type of the projectile ion

(in contrast to Champion’s values, which follow a unique law, independent of the impacting ion)

and, for a given value of E

ion

/Z, increase from protons (Z = 1) to neon ions (Z = 9). As can also be

seen from Figure14.6, our ratios of σ

/σ

compare reasonably well with those obtained from the

MI cross section calculations of Gervais et al. (2006) for protons and carbon ions (Z = 6). Although

such an accord is satisfactory here, it should be emphasized that the process of multiple ionization

of polyatomic molecules (including H

O) in heavy-ion collisions and in particular the effects due to

the phase, are an area where fundamental information is incomplete or even completely lacking in

some

cases, and where more experimental and theoretical work is expected and clearly desirable.

14.5.2.2

Fate

of m

ulticharged

ater

Cations

14.5.2.2.1

Acid–Base Re-Equilibration Reactions

Very little is known about the fate of multiply ionized water molecules in solution. In this work, the

rearrangement of these thermodynamically unstable multiply charged water cations is treated fol-

lowing the general mechanism proposed by Ferradini and Jay-Gerin (1998), which assumes that, in

liquid water, H

dissociates through acid–base re-equilibration processes. For example, for the

predominantly

formed doubly ionized water molecules, the overall dissociation reaction

H O H O 2H O O,

2 3

+ → + (14.19)

can be regarded as resulting from a two-step process involving two deprotonation reactions (the

two protons

being taken away by water molecules), namely,

H O H O H O OH ,

2 3

+ +

+ → +

followed

OH H O H O O.

+ → +

2 3

Similar reactions can be written for the triply and quadruply charged water cations [see reactions

(14.21)

and (14.22)], and for higher degree of ionization (n > 4) (see Table 14.3).

14.5.2.2.2

Fragmentation Caused by “Coulomb Explosions”

In gaseous water, MI is followed by the fragmentation of the ionized target as a result of the so-called

Coulomb explosion.* The mechanism of Coulomb explosion (e.g., Gemmell, 1980; Latimer, 1993) is

based on the simplied scenario where two or more electrons from a molecule are suddenly removed

by the incident projectile, so that the transiently formed highly ionized parent ion becomes unstable

(due to the Coulomb repulsion between the positive atomic fragment ions (holes) that can repel one

another apart) and rapidly dissociates into both charged and neutral fragments by bond breaking.

According to experimental results in the gas phase (e.g., Werner et al., 1995a,b; Olivera et al.,

1998; Gobet et al., 2001; Siegmann et al., 2001; Pešic´ et al., 2004; Alvarado et al., 2005; Legendre

et al., 2005; Luna and Montenegro, 2005; Sobocinski et al., 2006; Alvarado, 2007; Stolterfoht et al.,

2007, and references therein), three main, competing water dication fragmentation channels have

been identied (by the coincident detection of correlated fragments from a particular molecular

breakup),

namely,

* Fragmentation originating from violent binary collisions (involving small impact parameters) has also been observed

(Stolterfoht

et al., 2007).

378 Charged Particle and Photon Interactions with Matter

H O H H O

2+ + +

→ + + (14.24)

H O H OH

2+ + +

→ + (14.25)

H O H O H

2+ + +

→ + +

, (14.26)

while for ionization of higher multiplicity (q ≥ 3), the dominating fragmentation pathway involves a

three-body

breakup of the multi-ionized water molecule as follows:

H O H H O

2q q+ + + − +

→ + +

( )

. (14.27)

Only very few data exist on the cross sections (or probabilities) for these various possible water

polycation dissociation channels. For instance, Olivera et al. (1998) reported the values ∼6.3 × 10

−15

1.3 × 10

−15

, and 1.5 × 10

−15

(with an estimated uncertainty of ∼30%) for the fragment produc-

tion channels (14.24) through (14.26) coming from the double ionization of water under 6.7MeV/

nucleon Xe

44+

ion impact, respectively. These values are found to be ∼4–18 times less than the

corresponding single ionization cross section measured by these authors (∼2.4 × 10

−14

). As for

the triple ionization (q = 3), the cross section for the H

+ H

+ O

fragmentation channel (14.27)

obtained by Olivera et al. (1998) amounts to 2.5 × 10

−15

, an order of magnitude smaller than the

cross section for single ionization fragment production. Werner et al. (1995b) also reported that, for

100–350keV proton–H

O collisions, the fragmentation channel (14.24) has a cross section about

twice higher than the H

+ H

+ O

fragmentation (14.27), a result that is consistent with Olivera

etal.’s (1998) data. In another, more recent study, Pešic´ et al. (2004) investigated the fragmentation

table 14.3

radiolytic

roducts

nferred

from the

issociation

of m

ultiply

Charged w

ater

Cations*

n products

1 H

•

2 2H

+ O

4 4H

+ O

5 5H

•

OH + O

6 6H

+ O + O

+ O

8 8H

+ 2O

9 9H

•

OH + 2O

10 10H

+ O + 2O

Source: Ferradini, C., unpublished results, January 1994.

* (H

, n=1−10) (the molecule of water has 10 bound

electrons), as obtained by acid–base re-equilibration, in

the heavy-ion radiolysis of pure liquid water at high LET.

Radiation Chemistry of Liquid Water with Heavy Ions: Monte Carlo Simulation Studies 379

of water molecules following interaction with 2–90keV Ne

ions (p = 1, 3, 5, 7, and 9). These

authors observed a strong dependence of the fragment ion production cross sections on the projec-

tile charge state. They also found that their cross sections are almost two orders of magnitude larger

than those reported by Werner et al. (1995b) for the fragmentation of H

O following proton impact.

Although a great deal of attention is currently being devoted by different laboratories to the studies

of the inuence of the type, energy, and charge state of the impinging ion on the ion-impact-induced

fragmentation of water vapor, a detailed knowledge of the basic features of the explosive fragmen-

tation pattern of multiply charged water cations remains fragmentary. Clearly, there is a need to

explore these phenomena further.

In the liquid phase, it has been suggested that, following (single) ionization,* the H

•+

hole can

migrate rapidly by resonance electron transfer with neighboring water molecules until the ion–mol-

ecule reaction (14.14) localizes the hole (see above).

†

This proton transfer reaction (14.14) occurs

on the time scale of ∼10

−14

s (i.e., ∼10fs), time required for a single vibration of a water molecule.

Unfortunately, very little is known about the different dissociation pathways of H

(n ≥ 2) in

liquid water. To the best of our knowledge, the only previous studies devoted to this question are

those of Olivera et al. (1998), Gaigeot et al. (2007), and more recently Tavernelli et al. (2008).

Using arguments based on the ability of the medium to neutralize a charged species, Olivera et al.

(1998) tentatively extrapolated their water vapor multi-ionization results to liquid water. Among

other things, they concluded that, at least for the process of double ionization, the result of the

multi-ionization in liquid water may not be a direct Coulomb explosion of the molecule, but rather

a quick neutralization of the water polycation by the surrounding medium. In essence, this conclu-

sion was based on a comparison of the time involved in a dissociative Coulomb explosion process

‡

and some estimates of characteristic time scales of the competitive neutralization processes, such

as hole migration, geminate electron–cation recombination, and proton transfer reactions (∼1–10 fs;

see, e.g., Mozumder and Magee, 1975; Goulet et al., 1990; Meesungnoen et al., 2002b), in combina-

tion with energy transfer to the various modes of excitation of the surrounding medium. One further

argument against Coulomb explosion-induced fragmentation of the molecule (at least for the lowest

degree of ionization) is the “cage effect” observed for molecules in the condensed phase (Franck

and Rabinowitsch, 1934), which forces the ejected fragments to stay together (Olivera et al., 1998).

This cage recombination effect may signicantly alter product yields between the two phases (gas

phase

versus liquid).

their recent molecular dynamics simulations of a doubly ionized water molecule in the con-

densed phase, Gaigeot et al. (2007) and Tavernelli et al. (2008) were able to conrm the formation

of two H

ions and an oxygen atom assuming a Coulomb explosion mechanism of fragmentation.

Based on those calculations, these authors showed that double ionization leads to two main disso-

ciation pathways (in proportion to 84% of all H

fragmentations) for the production of oxygen

atoms

in liquid water, namely,

H O H H O H O O

2H O

2 55

+ + +

→ + +  → + ( %) (14.28)

H O H OH H O O

2H O

2 29

+ + +

→ +  → + ( %)

(14.29)

* From the Heisenberg uncertainty principle ΔtΔE ∼ ħ, the collision time required to know that an energy loss has taken

place

in ionization is, typically, ∼10

−16

†

By itself, H

•+

is stable, but in the presence of water, it dissociates, giving H

and an

•

OH radical.

‡

Most recent values of this time for the explosive dissociation of H

in liquid water, estimated from molecular dynamics

calculations and time-dependent density functional theory-based molecular dynamics simulations, are >1–15fs (Gaigeot

etal.,

2007) and <4

(Tavernelli et al., 2008), respectively.