Hatano Y., Katsumura Y., Mozumder A. (Eds.) Charged Particle and Photon Interactions with Matter - Recent Advances, Applications, and Interfaces

Подождите немного. Документ загружается.

770 Charged Particle and Photon Interactions with Matter

A X v J A X v v J J

v J

( , , , ) ( , , , , , )

α α=

∑

f f

(28.5)

where

A(X, α, v

, v, J

, J) is the Einstein A-coefcient for spontaneous transition from the excited state

│

α, v, J〉 back to

│

X, v

, J

〉 of the X

ground state

A(X, α, v, J) is the total emission probability (including transitions to lower singlet-gerade states

and

to the continuum levels of the X

state)

(α, v, J) is the predissociation + pre-ionization yield

Tr(X,

α, v, J, T) is the transmission function for self-absorption by resonance lines

The

volumetric excitation rate (excitations/s/cm

) at that point (x, y, z) is given by

′

∑

g v F E( , , ) ( )α σ,

J E N

i ij

e e

(28.6)

We use the index i to represent the initial electronic state |X, v

, J

〉, the index j to represent the excited

electronic state |α, v, J〉, N

= N

× f

and the excitation cross section, σ

= σ(v

, v, J

, J). The volu-

metric excitation rate g′(α, v, J, E

) is proportional to the population density N

of the molecule in

the initial vibrational–rotational level v

, J

, and the monoenergetic electron-impact ux F

due to the

electron beam current (Glass-Maujean etal., 2009). Equations 28.4 and 28.6 can be used to dene

a P, Q, or R branch rotational line emission cross section (without cascade) between two electronic

states

X and α:

σ α

η σ α

em ex

f f

( , , , , , )

( , , , )

( ) ( ,X v v J J

A X v v J J

A X v J

= −1 ,, , , , , )

v v J J E

i i

∑

(28.7)

The total thermally averaged excitation cross section for an electronic band system is dened by

Glass-Maujean

etal. (2009) as

(

)

∑

N E

i j

σ ( )

(28.8)

and

the corresponding thermally averaged emission cross section is given by

−

∑

σ ( )( )E

i j

(28.9)

The individual rovibronic excitation cross sections σ

) can be calculated from a known transition

probability and a measured excitation function for H

(Liu etal., 1998). For negligible self-absorp-

tion, the total band system volumetric photoemission intensity in Equation 28.4 is proportional to

the total emission cross section, σ

, and the neutral gas density, N

. The σ

is related to σ

indicated by comparing Equations 28.8 and 28.9. The ratio σ

divided by σ

gives the thermally

averaged emission yields for each of the ungerade Rydberg states in Table 28.1 (Glass-Maujean

etal.,

2009).

UV Molecular Spectroscopy from Electron Impact for Astrophysics 771

The UV wavelength calibration methodology developed at JPL has been used by several space-

craft missions (Hord etal., 1992; Esposito etal., 2004). This technique coupled with a relative

ow or swarm gas calibration developed at JPL (Ajello etal., 1989b) allows the determination

of absolute emission cross sections σ

from any of the ESL optical instrument systems. Recent

work by the ESL has established benchmark standards for absolute emission cross sections by

electron-impact uorescence measurements at 100 eV for reference gas H

(121.6 nm) σ

= 7.03

± 0.47 × 10

−18

(McConkey etal., 2008) and reference gas N

(120nm) σ

= 3.7 ± 0.5 × 10

−18

(Malone etal., 2008).

The absolute cross section for the emission of a particular spectral line λ induced by electron

impact on a target species M in a swarm gas experiment at 90° to the electron beam can be mea-

sured

at low pressure as (Johnson etal., 2003a,b)

λ λ

( )

( / ))

M =

1 (

KS p

b PI

− 3

(28.10)

table 28.1

lectronic-

band

Cross s

ections

and e

mission

ields

of h

singlet-Ungerade

tates

state

present

mission

ield

(%)

mission

ield

(%)

264

262

263 262

100

244

241

249

241

100

B′

d,e

21 21

53 56

25 24

11 11

43 46

−

21 18

100 100

B″

11 >4

2.2 1.6

20 <40

D′

9.3 7.1

1.6 1.0

18 14

D′

−

7.3

≥5.3

5.7 5.3

≤100

D″

3.2 >0.6 0.9 0.6 28 —

5pσ

— — 1.1 — — —

6pσ

— — 0.6 — — —

6pπ

— — 0.9 — — —

7pπ

— — 0.6 — — —

Source: Glass-Maujean,

M. etal., Astrophys. J. Suppl., 180, 38, 2009.

With

permission.

E = 100 eV and T = 300K. Unit is 10

−19

. σ

and σ

denote excitation and emission

cross sections, respectively. Certain numbers may not add up due to roundings. See Section

28.5.3

(Glass-Maujean etal., 2009) for estimated errors in cross sections.

Excitation cross sections include the excitation into the H(1s) + H(2l) continuum, which is

estimated from the calculation of Glass-Maujean (1986). Emission cross sections exclude

emission from the H(1s)+H(2l) continuum levels, but include continuum emission from the

excited discrete levels into the continuum levels of the X

state. Transitions to the X

continuum contribute 27.5% and 1.5%, respectively, to total emission cross sections of B

− X

and C

− X

(Abgrall etal. 1997). Note correction to B′

present σ

as suggested by Liu (private communication, 2010).

From Liu etal. (1998).

From Jonin etal. (2000).

Include excitations into the continuum levels of the B

state.

772 Charged Particle and Photon Interactions with Matter

where

is the photon signal

is a constant related to the geometry of the detector

is the sensitivity of the detector

is the instrumental polarization sensitivity of the system

is the polarization of the emitted radiation

is the gas pressure

is the electron beam current

The trapping of resonance radiation can reduce the emission rate signicantly at high gas pressure.

To avoid this complication, the gas pressure range is maintained at a sufciently low level. K is

determined from an intensity measurement of the known N

120 nm or H

121.6nm emissions, since

the instrumental factors are common to both target species (standard and target gas M). At 100 eV,

the atomic multiplets from dissociative excitation are unpolarized since many repulsive states con-

tribute

to the emissions.

28.4 present status oF h

, n

, Co, and so

28.4.1 h

–uv

Hydrogen is by far the most abundant element in the universe, playing a pivotal role in many physi-

cal and chemical processes. For example, in diffuse molecular clouds of the ISM and stellar atmo-

spheres, hydrogen chemistry permeates astronomical changes and provides the markers of stellar

evolution (Dalgarno, 1993, 1995). Over the past two decades, the observations of the ISM have

shown that H

is an active component of star formation. The changes that a star undergoes during

the formation and dying process are truly dramatic. These result in the most important interactions

between a star and its environment. Indeed, it is in this area of research that some of the most chal-

lenging astrophysical problems remain unanswered. UV and near-IR emissions from H

are among

the principal ways the interstellar gas cools following gravitational collapse during the star forma-

tion (Lepp and Dalgarno, 1996; Lepp etal., 2002). During the last 10 years, the observations of the

distribution of H

gas throughout the galaxy by FUSE have contributed to our understanding of stel-

lar evolution (Moos etal., 2000). Hence, H

has a unique and extraordinary position in astronomy

virtue of its UV spectroscopic signature of diverse energetic environments.

Molecular

hydrogen is the simplest molecule from a structural point of view, but its band spectra

are quite complex and extend from UV to near-IR wavelengths due to the relatively large values of

rotational constants for all the electronic states. An accurate model of the H

spectrum has been

a fundamental building block for understanding the chemistry of the solar system and ISM. Until

recently, a 50%–200% uncertainty existed for some of the excitation cross sections and transition

probabilities of the singlet-gerade (even) states of H

and HD, i.e., the states that provide VOIR

cascade excitation to the Lyman and Werner bands (Ajello etal., 2005b; Aguilar etal., 2008). The

recent study of H

emission cross sections (Aguilar etal., 2008) is the rst of the VOIR wave-

length range (300–1100nm) in 50 years, since the pioneering work of Dieke and coworkers (Dieke,

1958; Dieke and Cunningham, 1965; Crosswhite, 1972) who demonstrated the existence of over

100,000 rotational lines and transitions in this wavelength region involving 15 electronic states of

(Crosswhite, 1972). The complete single-scattering VOIR spectra of the H

and HD gerade–

ungerade band systems had never been studied in the laboratory, nor have the oscillator strengths

been accurately calculated until recently. The theoretical oscillator strength study by the Meudon

Observatory (Aguilar etal., 2008 and references there in) involves detailed calculations of emission

transition probabilities and line positions of individual rotational lines of the nine coupled EF, GK,

HH, K, P

states and I, R

and J, S

states. All of these coupled states contribute heavily to

the UV spectrum through cascading. Comparing the laboratory spectra to model calculations based

UV Molecular Spectroscopy from Electron Impact for Astrophysics 773

on the theoretical oscillator strengths, many irregularities (intensity and wavelength positions) in

the VOIR were explained (Aguilar etal., 2008), although many remain unaccounted for and are

being

reevaluated.

The

ESL has provided the same molecular parameters for the singlet-ungerade (odd) states of

and HD (and even of D

) to an accuracy of 10% (i.e., states that lead to the direct excitation of

the Lyman and Werner bands) (Liu etal., 1995; 1998; 2000; 2002; 2003; Abgrall etal., 1999; Ajello

etal., 2005b; Glass-Maujean etal., 2009). These will aid in the studies of the ISM and planetary

atmospheres,

where both types of electron-excited transitions take place.

Very

accurate synthetic spectral models of H

for UV astronomy have been developed recently

(Dols etal., 2000; Jonin etal., 2000; Liu etal., 2003; Gustin etal., 2004; Glass-Maujean etal.,

2009). These models properly account for cascade, predissociation, and resonance effects by utiliz-

ing high-resolution measurements of spectra and cross sections (Glass-Maujean etal. 2009). We

now understand that the complexity of the H

band system arises from intense conguration interac-

tion, predissociation, and autoionization that are present in the 11–16eV electronic energy region of

the Rydberg and valence (RV) states. A simplied adiabatic energy level diagram of H

exhibiting

the strongest allowed excitation process producing the B → X (Lyman bands) and the strongest

optically

forbidden process producing the EF → B (Lyman band cascade) is shown in Figure 28.7.

τ = 21 ns

τ = 99 ns

τ = 200 ns

τ = 1.1 μs

τ = 2 ns

0 0.8 1.6

Internuclear distance (Å)

Potential energy (eV)

2.4 3.2

E, F

G, K

hν

(Visible-IR)

hν

(MUV)

hν

(Lyman bands)

Figure 28.7 A partial energy level diagram for H

showing the energy regions for the VOIR (gerade-

ungerade) singlet transitions and the UV (ungerade-gerade) transitions (Aguilar etal., 2008). The lowest-lying

ungerade–gerade transition is B

→ X

(direct excitation of the Lyman bands) and the lowest-lying

gerade–ungerade transition is E, F

→ B

→ X

(cascade excitation of the Lyman bands). The

approximate lifetimes for some of the direct (dipole-allowed) and cascade (optically forbidden) vibronic

states are listed.

774 Charged Particle and Photon Interactions with Matter

Shemansky and Ajello (1983) identied, for the rst time, the presence of the two most impor-

tant UV emissions in the observations by the Voyager I, II spacecraft for application to the outer

planets. These are the Rydberg series of H

, namely,

1sσnpσ (B, B′, B″, n = 2, 3, 4) → X

and

1sσnpπ (C, D, D′, D″, n = 2, 3, 4, 5) → X

through n = 5, along with optically forbidden exci-

tation of X

→ EF

followed by dipole-allowed cascade of EF

→ B

, which were found

to be the indicators of electron energy and were the source of the principal (overlapping) spectral

contributions to the Voyager UV spectrum (Shemansky and Ajello, 1983; Ajello et al., 1984; Jonin

etal., 2000). Prior to this work, the Lyman and Werner band systems (n = 2) were thought to be the

only bands involved in the Voyager analysis (Broadfoot etal., 1979, 1981a,b), as shown in Figure

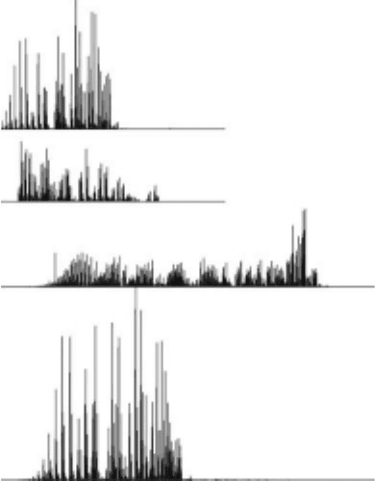
28.3a. In Figure 28.8, we show (to scale) a composite of the rst four (n = 2,3) of the 15 singlet-state

band

systems contributing directly to the H

UV spectrum (Liu etal., 1995; Ajello etal., 2001).

Over the last 20 years, a study has been carried out of the remaining singlet-ungerade states

in the high-resolution EUV emission spectra of molecular hydrogen excited by electron impact

at 100eV under optically thin, single-scattering experimental conditions (Jonin etal., 2000; Liu

etal., 2000; Glass-Maujean etal., 2009). A portion (94.5–96 nm) of the high resolution spectrum

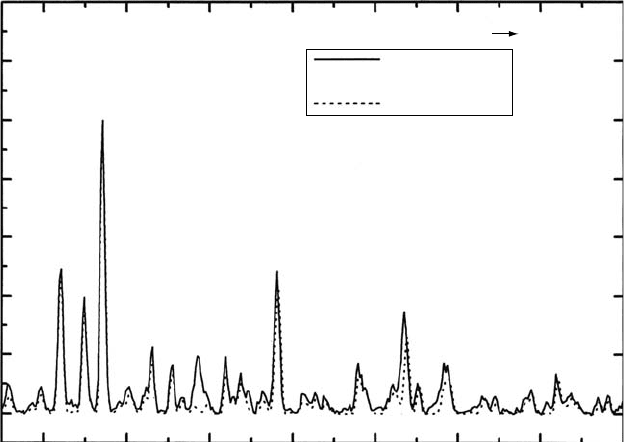
(FWHM = 0.0085nm) spanning the wavelength range of 80–115nm is shown in Figure 28.9. The

total emission cross sections for D

, D′

, D″

, B′

, B″

states for the n = 3 and four

transitions to the ground state were obtained at 100eV by measuring the emission cross section

of each rotational line. The Lyman and Werner bands have the largest emission cross sections at

100 eV with values of 2.64 × 10

−17

and 2.44 × 10

−17

, respectively (Liu etal., 1998; Jonin

etal., 2000; Glass-Maujean etal., 2009). Glass-Maujean etal. (2009) now give the 100eV electronic

Rydberg band system emission and excitation cross sections through n = 7. We list these cross sec-

tions in Table 28.1.

1sσnpπ n = 3

C(Werner)

1sσnpπ n = 2

800 1000 1200

Wavelength (Å)

Intensity (arb. units)

1400 1600 1800

1sσnpσ n = 3

B(Lyman)

1sσnpσ n = 2

Figure 28.8 Model line spectrum of the B

→ X

, C

→ X

′

∑ → ∑

1 1

u g

X ,

and D

→ X

band systems of H

at 300K and 100 eV without self-absorption. The model is based on the line positions and

transition probabilities of Abgrall etal. (1993a,b,c, 1994, 1997) and the electron emission cross sections of

Liu

etal. (1998).

UV Molecular Spectroscopy from Electron Impact for Astrophysics 775

For J values of 1–4 at laboratory temperatures of ∼300 K, the emission yields of each rovibronic

level of the npσ

and npπ

states are determined by comparing observed and calculated rota-

tional spectra (Glass-Maujean etal., 2009). Since Jovian aurora take place at elevated rotational

temperatures of 500–1200K (Gustin etal., 2004), models of the EUV require predissociation yields

to high J-value (∼J = 5–10) (Glass-Maujean etal., 2009). In summary, the mean emission yields of

the B

, C

, B′

, D

−

, B″

, D′

−

, D″

states, dened previously,

are 99%, 98%, 53%, 43%, 100%, 20%, 18%, 78%, 28%, respectively, at 100eV and 300K (Glass-

Maujean

etal., 2009) (see Table 28.1).

Using

the Q1(1,4) Werner rovibronic line and the P1,2,3(8,14) Lyman rovibronic line, we devel-

oped an accurate modied Born model for the excitation cross section (without cascade) of the

Lyman and Werner bands for use in the electron transport codes of planetary atmospheres and

astrophysics. The model for 0–1.2keV electron impact energy is shown in Figure 28.10 with the

updated Lyman and Werner 100eV cross sections (Liu etal., 1998; Glass-Maujean et al., 2009).

Glass-Maujean

etal. (2009) give estimates for excitation functions for the B″ and D′-states.

accurate model of a 100 eV high-resolution laboratory electron-impact-induced uorescence

spectrum, based on the calculated transition probabilities and predissociation yields of Abgrall

etal., (1993a,b,c) and Glass-Maujean etal., (2007a,b,c,d, 2008), veries adiabatic transition proba-

bilities for RV rovibronic states of n = 4–8 and nonadiabatic transition probabilities for n = 2–4. The

synthetic spectrum is capable of modeling over 98% of the laboratory e + H

emission spectrum at

room temperature 300K and 100eV electron energy. Furthermore, the Lyman and Werner emission

cross section energy dependence from Liu etal. (1998) for the B and C states, and the rotational line

positions from Roncin and Launay (1994) have allowed us to generate an accurate (∼15% accuracy

from 79 to 90nm and ∼5% from 90 to 175nm) synthetic high-resolution rotational line spectrum of

the singlet-ungerade states in the UV with electron energies of 10–1000eV. Using the recent work

1.4

1.2

1.0

e (100 eV)+ H

(300K) B, B΄, C, D

Experiment

Δλ

FWHM

=140 mÅ

Theory

0.8

0.6

0.4

0.2

0.0

946 948

1(4,4)Q D-X

0(3,0)R C-X

1(14,0)R B-X

3(4,4)Q D-X

2(3,0)Q C-X

1(2,3)Q D-X

2(14,0)P B-X

atomic line 1s-5p

3(3,0)Q C-X

3(3,0)P C-X

3(2,3)P D-X

3(19,1)P B-X

3(2,3)Q D-X

2(5,1)Q C-X

1(0,2)R D-X

4(3,0)R C-X

1(0,2)Q D-X

1(13,0)R B-X

3(5,1)P C-X

3(0,2)Q D-X

2(13,0)R B-X

3(0,2)Q D-X

2(13,0)P B-X

5(3,0)P C-X

1(0,2)R D-X

1(1,2)R B-X

3(18,1)P B-X

1(5,1)R C-X

1(3,0)Q C-X

950 952

Wavelength (Å)

Calibrated intensity (arb. units)

954 956 958 960

Figure 28.9 Over-plot of the observed spectra (FWHM = 140 m Å) and model spectra of H

for the low

pressure regime of background pressure of 1.2 × 10

−5

Torr. The high-pressure spectrum spans the wavelength

range from 945 to 960 Å. The model uses the transition probabilities of Abgrall et al. (1993a,b,c, 1994, 1997)

with a transmission function for self-absorption at 100 eV electron-impact energy and a gas temperature

of 300 K.

776 Charged Particle and Photon Interactions with Matter

of Glass-Maujean etal. (2007a,b,c,d, 2009) and comparing the synthetic spectra through n = 8 with

the ESL high-resolution spectra, it has been possible to accurately model direct excitation to the

high-lying, ungerade-singlet Rydberg states. The high-lying states contribute signicantly to the

EUV

spectrum below 90

nm.

28.4.2 h

–voir

The electron-impact-induced uorescence spectrum of H

from 330 to 1000nm at 20 and 100 eV

was reported for the rst time (Aguilar etal., 2008) at high resolution (λ/Δλ = 10,000). The spectrum

contains the gerade Rydberg series of singlet states EF

, GK

, H

−

, I

, J

…→ B

Π and the Rydberg series of triplet states dominated by the d

, k

, j

→ a

. These

VOIR

bands were recently observed by the Cassini Imaging Subsystem (ISS) in the visible/near IR

lters viewing the Saturn aurora (Dyudina etal., 2007). STIS or Cosmic Origins Spectrograph

(COS) might also be able to observe these directly on the outer planets. A model VOIR spectrum

of H

from 750 to 1000nm, based on newly calculated transition probabilities and line positions,

including rovibrational coupling for the singlet-gerade states, is in excellent agreement with the

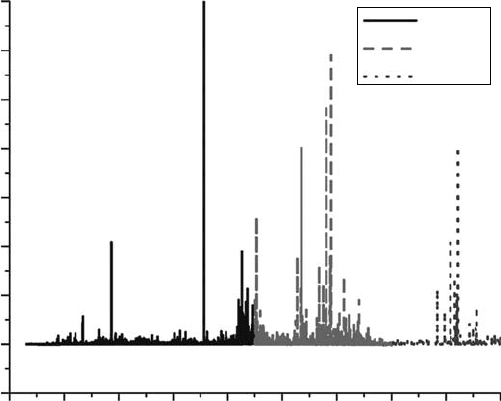
observed intensities. Figure 28.11 shows the experimental data of high-resolution (0.07nm FWHM),

electron-impact-induced UV-VOIR emission spectra from 330 to 1200nm at 100eV.

The absolute emission cross section values for excitation to the singlet-gerade states at 100eV

for optically thin, single-scattering condition was measured to be 4.58 ± 1.37 × 10

−18

; for

excitation

to the triplet states at 20

eV,

the cross section was 1.38 ± 0.41 × 10

−19

(Aguilar etal.,

2008). The singlet-gerade emission cross sections are due to cascading into the UV (including the

Lyman and Werner band systems), and the triplet-state emission cross sections are due to cascade

dissociation of the H

− b

) continuum that produces fast hydrogen atoms (Ajello and

Shemansky, 1993).

In a complementary type of experiment to the VOIR, a newly devised pulsed spectroscopic

technique demonstrated (Dziczek etal., 2000; Liu etal., 2002) that the gerade series (EF, GK, H

−

I,J…) make a signicant contribution (∼50% at 20eV) to the UV spectrum of H

, by virtue of their

cascade to states that correlate to H(1s) and H(2s,2p) (i.e., the upper states of the Lyman and Werner

300

250

100 eV

Werner

Lyman

200

150

100

0 100 200 300 400 500

Excitation energy (eV)

σ (10

–19

)

600 700 800 900 1000 1100 1200

Figure 28.10 Total cross section (in 10

−19

) of the Lyman and Werner band systems at 300K. The cross

section of the Lyman band system is represented by dots, while that of the Werner band system is shown by

the

solid line (Liu etal., 1998; Glass-Maujean etal., 2009).

UV Molecular Spectroscopy from Electron Impact for Astrophysics 777

bands, respectively). This large cascade cross section is important because the mean secondary

electron energy in planetary thermosphere and in cosmic-ray-induced ionization in molecular cloud

lies between 20 and 100eV (Gredel etal., 1989; Ajello etal., 2002a, 2005b). The intensity of UV

resonance transitions excited by electron impact is determined by both the direct and cascade pro-

cesses. The lifetime (τ) for decay by spontaneous emission from a dipole-allowed transition is typi-

cally short (<10 ns, see Figure 28.7). To measure the electron-impact cascade spectrum of the

n= 2 H

Lyman band system (B

− X

), we use the longer lifetimes (>30ns, see Figure 28.7)

for cascade from higher lying states (EF, GK, H

−

H, …

). The pulsed gun technique takes advan-

tage of the drastic difference in lifetimes (∼1ns vs. ∼100ns) between the ungerade (direct) states and

singlet-gerade (cascade) states, respectively. The rst laboratory studies and modeling of the UV

spectrum of H

attributed to cascade used a pulsed gun technique to separate cascade and direct

excitation effects (Dziczek etal., 2000; Liu etal., 2002). Pulsing the electron gun and gating the

photon detector to measure the cascade spectrum after the directly excited population decays also

allows a determination of the cascade cross section because the spectral pattern from direct excita-

tion and cascade are different. Direct excitation produces a large population in the B-state centered

at v′ = 7, whereas cascade populates the lower vibrational levels most strongly, beginning at v′ = 0.

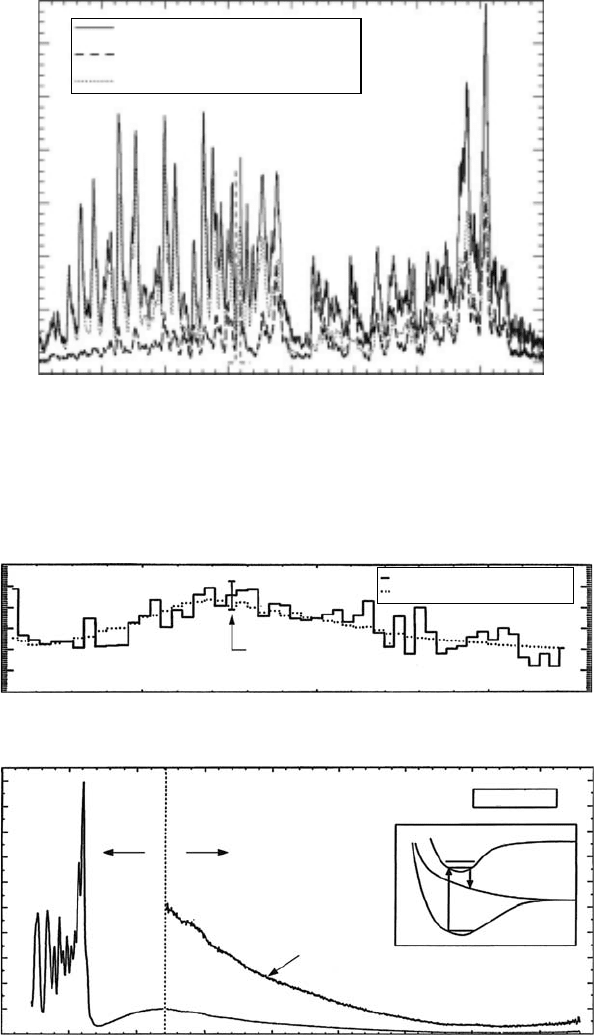
studying Figure 28.12, we clearly see that there are regions in the FUV spectrum dominated by

cascading. The most important two wavelength regions that are exclusively (more than 90%) due

to cascade lie near the 133–135 and 139–142nm. These regions correspond to the rotational lines of

the (0,1) and (0,2) vibrational bands of the B−X Lyman bands, the two strongest bands of the v′ = (0, v″)

progression. The strongest feature in the cascade spectrum occurs at 161nm and involves the super-

position

of rovibronic transitions from v′ = 4, 5, and 6.

The

medium-resolution spectrum at 14eV is shown in Figure 28.13b in both the FUV- and mid-

dle ultraviolet (MUV) portion of the VOIR extending from 100 to 530nm, including the Lyman

bands and the H

→ b

) continuum (James etal., 1998b). The rst detection of the H

a-b

continuum MUV emission in astronomy (Pryor etal., 1998) was made through comparison to our

0.35

0.30

0.25

0.20

0.15

0.10

0.05

0.00

Hβ

Hα

EF-B bands

Grating 2

Grating 3

Theory

–0.05

3000 4000 5000 6000 7000 8000

Wavelength (Å)

Cross section (Mb)

9000 10000 11000 12000

Figure 28.11 High-resolution spectrum with intensity in units of cross section (cm

) for the electron-impact-

induced uorescence spectrum from 3,300 to12,000Å of H

at 100eV in three wavelength regions: (1)grating-2

(3300–7500Å) in black, grating-3 (7,500–10,000Å) in long-dash light gray, and theory (10,000–12,000 Å) in

short-dash dark gray. The Hα multiplet is off scale (Aguilar etal., 2008).

778 Charged Particle and Photon Interactions with Matter

Relative intensity (arb. units)

20 eV DC spectrum

20 eV pulse spectrum

Model 20 eV spectrum (no cascade)

3.0

2.5

2.0

1.5

1.0

0.5

0.0

90 100 110 120

Wavelength (nm)

130 140 170150 160

Figure 28.12 The 20 eV steady state (cascade + direct) spectrum and linear regression t using the 20 eV

pulsed-gun cascade spectrum and 20eV model direct excitation spectrum. H Lα is included in the model as

monochromatic line. The photon gate delay for the pulsed-gun spectrum is 135

(Dziczek etal., 2000).

400

300

200

100

Counts

–100

–200

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

100 150

F-PMT E-PMT

(a–b)

14 eV

a–b

H+H (e–3 eV)

200 250 300

Wavelength (nm)

(b)

Relative intensity (arb. units)

350 400 450 500

2000 2500

(a – b)

(First observation in astronomy)

Dark side –Scaled day side

Lab 14 eV e

–

on H

spectrum

Wavelength (Å)

(a)

Laboratory

Galileo

MUV spectrum

3000

Figure 28.13 (a) The rst observation in astronomy of the H

a-b continuum. Jupiter darkside aurora spec-

trum overplotted with a 14eV laboratory spectrum (Proyor etal., 1998). (b) The combined FUV spectrum,

measured with an EMR F-photomultiplier (CeTe photocathode), and the MUV spectrum, measured with an

EMR –E-photomultiplier, of H

corrected for instrument sensitivity produced by electron impact at 14 eV

measured at 1.7nm FWHM at 300 K and 2 × 10

−4

Torr background gas pressure in the crossed-beams mode

(James

etal., 1998a,b).

UV Molecular Spectroscopy from Electron Impact for Astrophysics 779

laboratory spectrum (James etal., 1998b). We show the comparison of the Galileo observation of

the

Jupiter dark side aurora with the laboratory spectrum in Figure 28.13a.

The

set of triplet states above the b

repulsive state leads to continuous emission with

high-velocity H-atoms (∼3 eV per atom) formed in the spontaneous dissociation. This process

of electron excitation is shown in the inset to Figure 28.13b. The b

state, which is the lowest

lying repulsive state (1sσ) (2pσ), can be excited to the continuum by direct excitation from the

ground X

state or via cascade from the a

− b

continuum. The a

state produces the

strongest triplet-state emission from the process H

→ b

), leading to the famous a-b

continuum, for electron energies below 30 eV (Ajello and Shemansky, 1993). The a

state is

strongly populated by cascade from the c-, d-, and e-states. The excitation function for the a-b

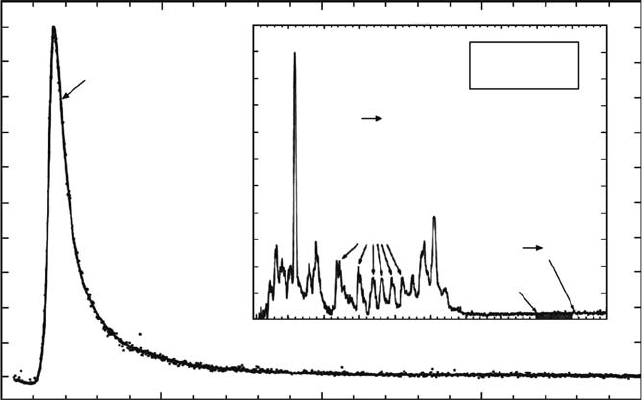
continuum is shown in Figure 28.14. The gure (see inset) also shows a 20 eV spectrum indi-

cating relative importance and wavelength region for strong cascade and a-b continuum in the

FUV. The triplet states are the major source of dissociation of the hydrogen molecule by electron

impact.

Optical excitation functions of the triplet states have also been measured by few experi-

menters in the VOIR. Dieke (Crosswhite, 1972) has shown the presence of many triplet band

systems in his discharge emission experiments with the strongest and most extensive to be the

Fulcher-α band system (3pπ d

→ 2sσ a

). The emission cross sections of the Fulcher-α

diagonal bands (Δv = 0) have been studied by Möhlmann and de Heer (1976). Those processes

leading to triplet emissions arise rst from singlet–triplet excitation. The excitation occurs by

electron exchange, which is characterized by a fast rise and decrease in the emission cross

section within a few eV of threshold (see Figure 28.14). Tawara etal. (1990) have reviewed

the excitation cross sections of the X → 2sσ a

, 2pσ b

, 2pπ c

, and 3pσ e

states

by electron-energy-loss experimental techniques. Emission from the e

triplet state e → a

transition was observed by Dieke (1958) and Dieke and Cunnigham (1965) as well as by Dieke

in a couple of early publications as referenced by Huber and Herzberg (1979) and Crosswhite

(1972). The c-state, whose v′ = 0 level lies below the a-state, is forbidden for transitions to the

b- and X-state. Thus, there are two Rydberg series terminating in the two bound triplet states,

1.0

0 50 100

Energy (eV)

Relative intensity (arb. units)

150 200

210200190180170160

Wavelength (nm)

150140130120110

(a–b, 190 nm)

Δλ=10 nm

+e (20 eV)

Δλ=0.5 nm

Direct

cascade

Q =190 nm

Lyman bands

121.57 nm

Relative cross section (arb. units)

Figure 28.14 The H

→ b

) excitation function from 0 to 200eV (Ajello and Shemansky, 1993).

The inset is a combined FUV and MUV spectrum of H

→ b

) continuum at 20eV. The cross-hatched

area

shows the band pass of the spectrometer for the excitation function measurement.