Hua C., Wong R. Differential Equations and Asymptotic Theory in Mathematical Physics
Подождите немного. Документ загружается.

322
number of canals.
5.4.
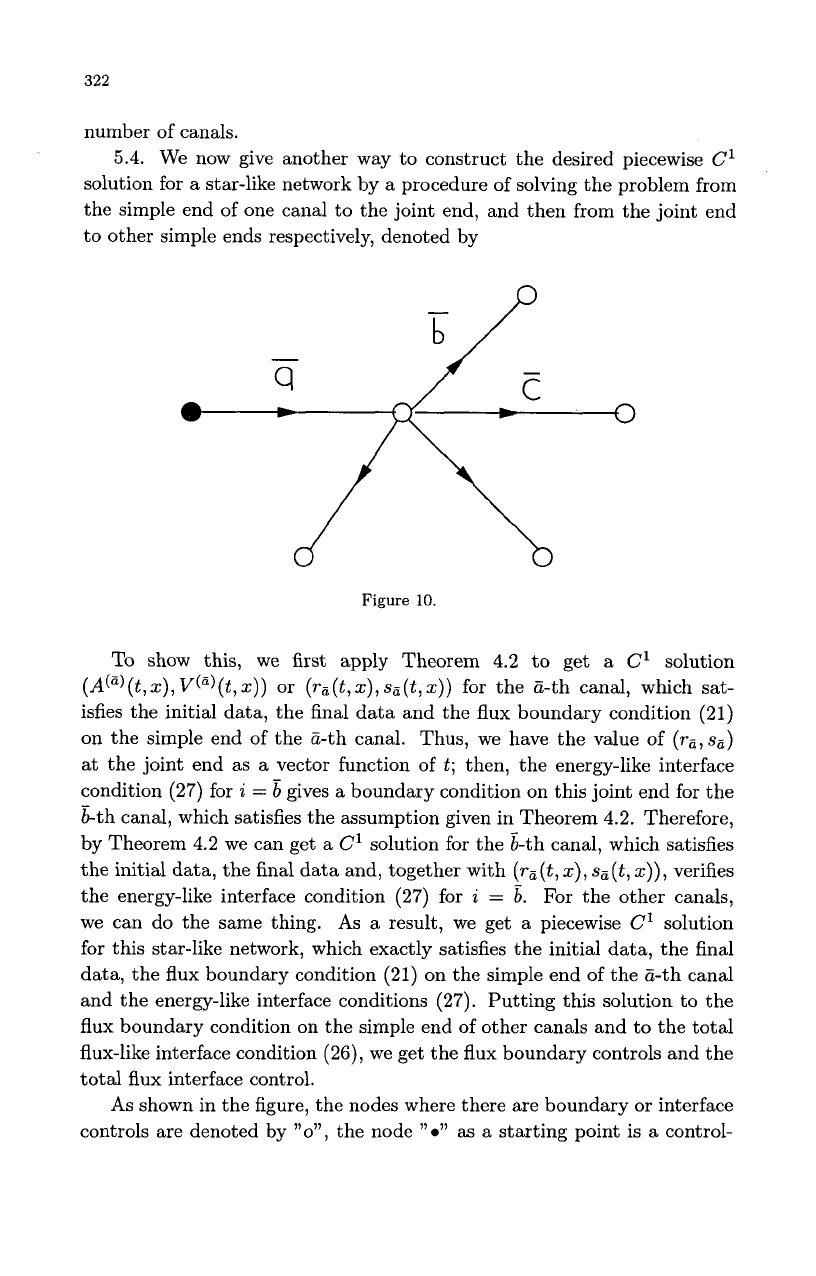
We now give another way to construct the desired piecewise
C1
solution for
a
star-like network by a procedure of solving the problem from
the simple end of one canal to the joint end, and then from the joint end
to other simple ends respectively, denoted by
9
b
Figure
10.
To show this, we first apply Theorem
4.2
to get
a
C1
solution
(A(')(t,
z),
V(')(t,
z))
or
(rs(t,
z),
s'(t,
z))
for the a-th canal, which sat-
isfies the initial data, the final data and the flux boundary condition
(21)
on the simple end of the 6-th canal. Thus, we have the value of
(rii,sa)
at the joint end as a vector function of
t;
then, the energy-like interface
condition
(27)
for
i
=
6
gives
a
boundary condition on this joint end for the
Lth canal, which satisfies the assumption given in Theorem
4.2.
Therefore,
by Theorem
4.2
we can get
a
C1
solution for the 6-th canal, which satisfies
the initial data, the final data and, together with
(rs(t,
z),
ss(t,
z)),
verifies
the energy-like interface condition
(27)
for
i
=
6.
For the other canals,
we can do the same thing.
As
a result, we get
a
piecewise
C1
solution
for this star-like network, which exactly satisfies the initial data, the final
data, the flux boundary condition
(21)
on the simple end
of
the a-th canal
and the energy-like interface conditions
(27).
Putting this solution to the
flux boundary condition on the simple end of other canals and to the total
flux-like interface condition
(26),
we get the flux boundary controls and the
total flux interface control.
As
shown in the figure, the nodes where there are boundary or interface
controls are denoted by
"o",
the node
"0"
as
a starting point is
a
control-
323
free one,
”+”
dedicates the direction along which the problem is solved. In
this situation, the number of controls is still equal to the number of canals,
however, there is a total flux control acting on the joint end.
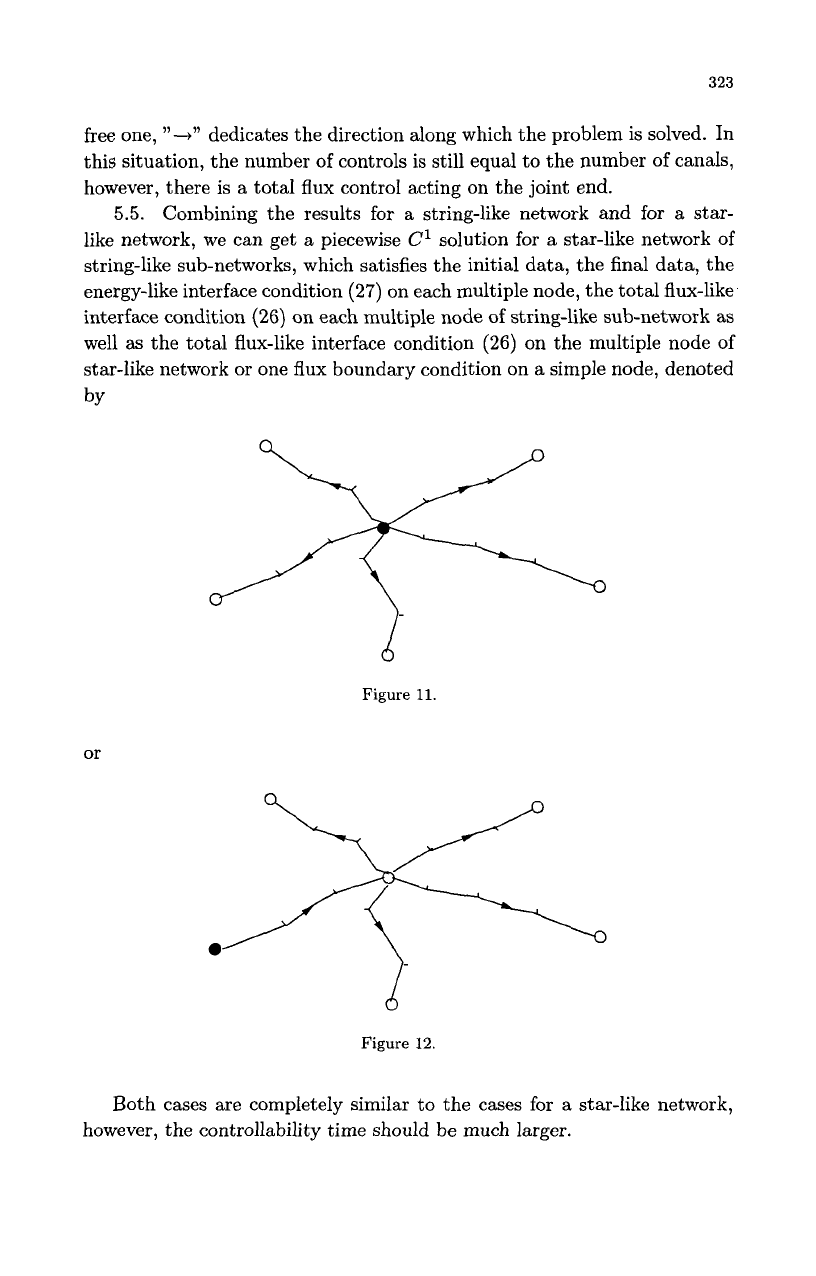
5.5.
Combining the results for a string-like network and for
a
star-
like network, we can get
a
piecewise
C1
solution for
a
star-like network of
string-like sub-networks, which satisfies the initial data, the final data, the
energy-like interface condition (27)
on
each multiple node, the total flux-like
interface condition (26) on each multiple node
of
string-like sub-network
as
well
as
the total flux-like interface condition (26) on the multiple node
of
star-like network or one flux boundary condition on a simple node, denoted
by
Figure 11.
or
0
Figure 12.
Both cases are completely similar to the cases for
a
star-like network,
however, the controllability time should be much larger.
324
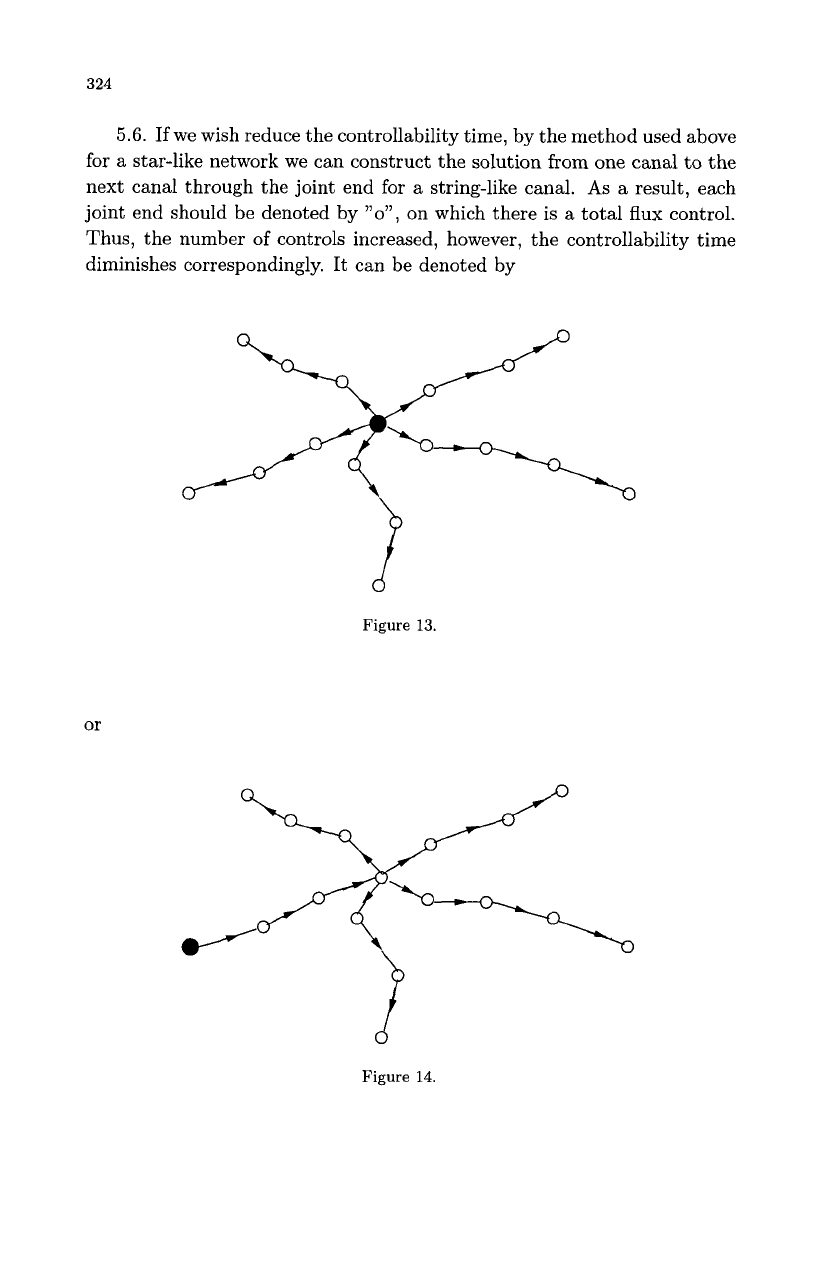
5.6.
If
we wish reduce the controllability time, by the method used above
for a star-like network we can construct the solution from one canal to the
next canal through the joint end for
a
string-like canal.
As
a
result, each
joint end should be denoted by
',o',,
on which there is
a
total flux control.
Thus, the number
of
controls increased, however, the controllability time
diminishes correspondingly. It can be denoted by
Figure
13.
or
Figure
14.
325
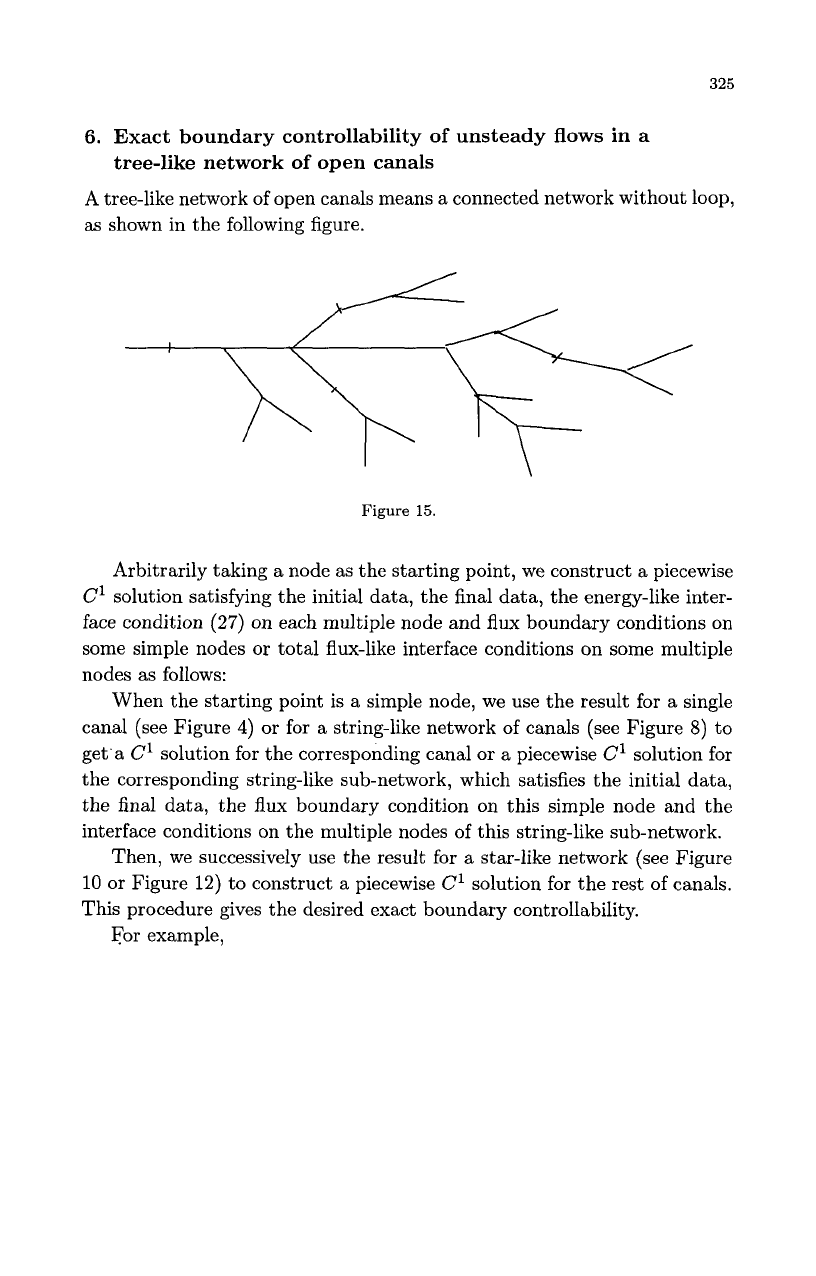
6.
Exact boundary controllability
of
unsteady
flows
in a
tree-like network
of
open canals
A tree-like network of open canals means a connected network without loop,
as
shown in the following figure.
Figure
15.
Arbitrarily taking a node
as
the starting point, we construct a piecewise
C1
solution satisfying the initial data, the final data, the energy-like inter-
face condition
(27)
on each multiple node and flux boundary conditions on
some simple nodes
or
total flux-like interface conditions on some multiple
nodes as follows:
When the starting point is a simple node, we use the result for
a
single
canal (see Figure
4)
or
for
a string-like network of canals (see Figure
8)
to
get'a
C1
solution for the corresponding canal or a piecewise
C1
solution for
the corresponding string-like sub-network, which satisfies the initial data,
the final data, the flux boundary condition on this simple node and the
interface conditions on the multiple nodes of this string-like sub-network.
Then, we successively use the result for
a
star-like network (see Figure
10
or Figure
12)
to construct a piecewise
C1
solution for the rest of canals.
This procedure gives the desired exact boundary controllability.
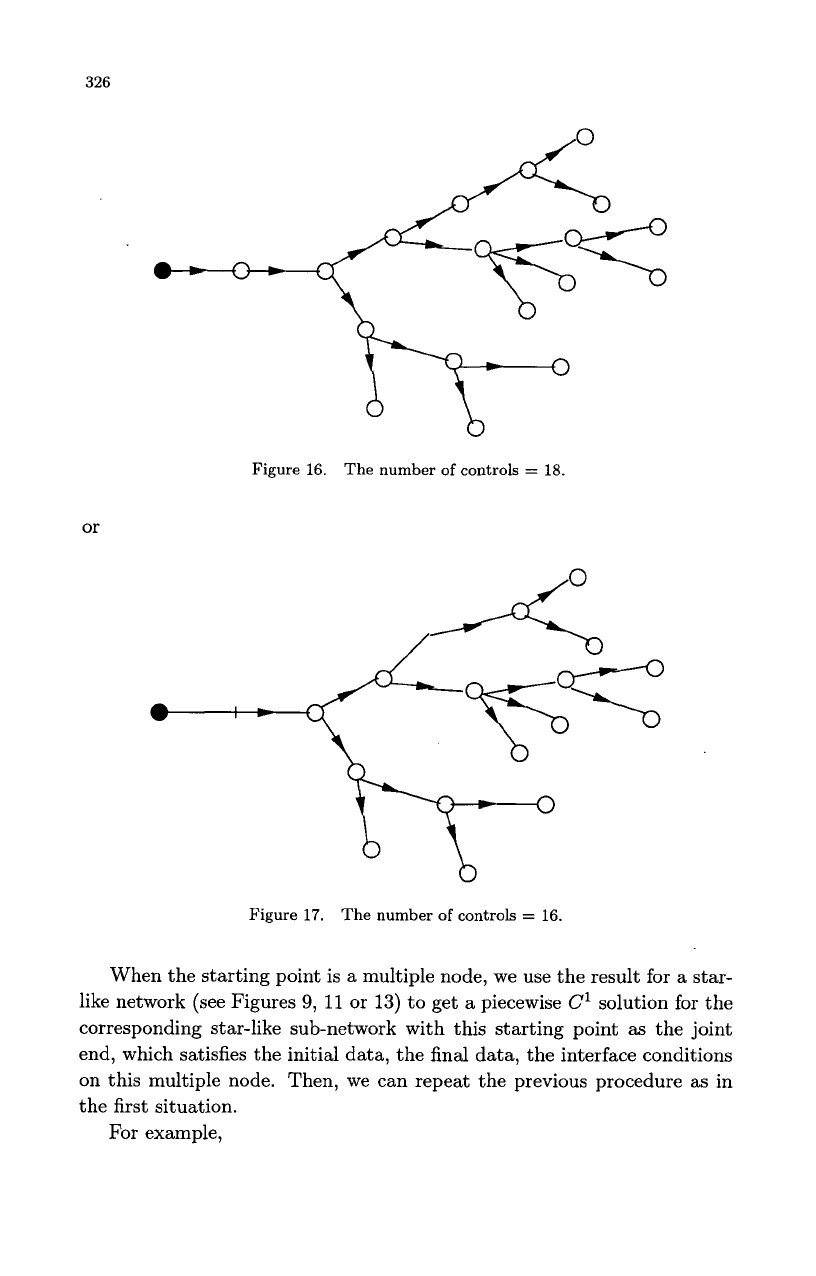
For
example,
326
Figure
16.
The number
of
controls
=
18.
or
Figure
17.
The number
of
controls
=
16.
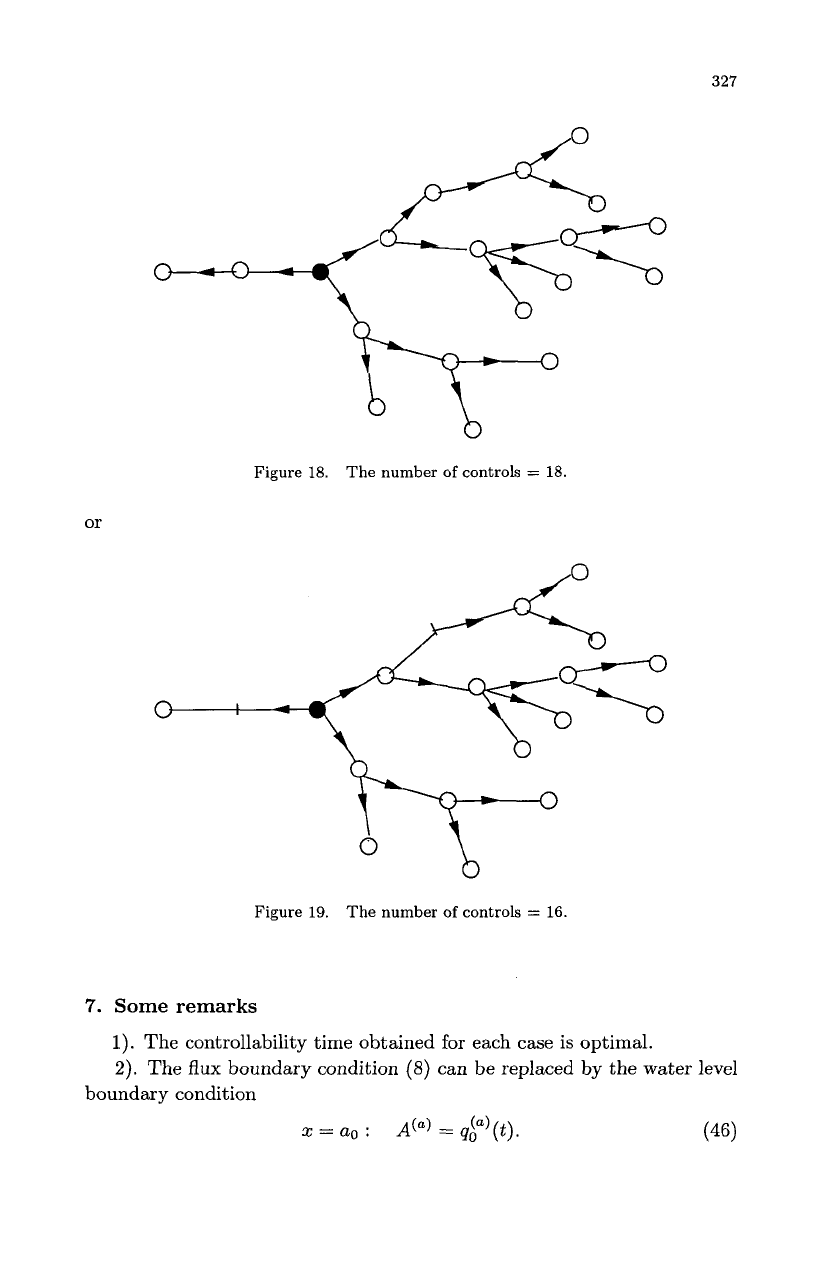
When the starting point is a multiple node, we use the result for
a
star-
like network (see Figures
9,
11
or
13)
to get a piecewise
C1
solution for the
corresponding star-like sub-network with this starting point
as
the joint
end, which satisfies the initial data, the final data, the interface conditions
on this multiple node. Then, we can repeat the previous procedure as in
the first situation.
For example,
327
Figure
18.
The number
of
controls
=
18.
or
Figure
19.
The number
of
controls
=
16.
7.
Some remarks
1).
The controllability time obtained for each case is optimal.
2).
The flux boundary condition
(8)
can be replaced by the water level
boundary condition
2
=
a0
:
A(")
=
qk)(t).
(46)

328
Moreover, the energy-like interface conditions
(10)
can be also replaced
by the water lever interface conditions
+
Yb(2)
=
&(A("))
+
yb(")
(i
=
6,
E,
. .
.).
(47)
3).
If
one considers the friction, in
a
network of open canals, Saint-
Venant system
(3)
becomes
+
=
0,
+
F,(A("), If("))
=
0,
(u=l,...
,N),
where, for
a
=
1,
. .
.
,
N,
S(")
is still given by
(4),
and
V,Fi(Ai,
V,)
2
0.
(50)
In this case, for any given equilibrium state
(A("), V("))
=
(At),
0)
with
Aio
>
0
(a
=
1,
. .
.
,
N),
we still have the exact boundary controllability.
4).
Since both the initial and final states belong to a neighbourhood of
an arbitrarily given subcritical equilibrium state, our results give only the
local exact boundary controllability for unsteady flows in canals, however,
that is enough to get the corresponding global exact boundary controlla-
bility. In fact, in order to drive any given initial state in
a
neighbour-
hood of a subcritical equilibrium state
(At),
&("I)
(a
=
1,.
.
,
N)
to any
given final state in a neighbourhood of another subcritical equilibrium state
(A(,"),V$"))
(a
=
l,...
,N),
it suffices to use the previous results to first
drive the initial state to the equilibrium
(At), Vd"')
(u
=
1,.
.
,
N),
then
successively transfer equilibrium states to
(A(,"), V,'"')
(a
=
1,
.
. .
,
N),
and
finally reach the final state.
Thus, we get the corresponding global exact boundary controllability,
however, the controllability time must be enlarged many times.
References
1.
B.
de Saint-Venant, Thkorie du mouvement non permanent des eaux, avec
application aux crues des rivihres et l'introduction des makes dans leur lit,
C.
R.
Acad. Sci.,
73,
147
237
(1871).
G.
Leugering and
E.
G.
Schmidt, On the modelling and stabilization
of
flows
in networks
of
open canals,
SIAM
J.
Control
Optim.
41,
164
(2002).
2.

329
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
M. Gugat and G. Leugering, Global boundary controllability of the de
St.Venant equations between steady states,
Ann. I.
H.
Poincare‘, Analyse
Non Line‘aire
20,
1
(2003).
J.-M.
Coron, B. d’Andrka-Novel and
G.
Bastin, A Lyapunov approach to
control irrigation canals modeled by Saint-Venant equations, in CD-Rom
Proceedings, Paper
F1008-5,
ECC99, Karlsruhe, Germany,
(1999).
J.
de Halleux,
B.
d’Andr6a-Nove1, J.-M. Coron and
G.
Bastin, A Lyapunov
approach for the control of multi reach channels modelled by Saint-Venant
equations, in CD-Rom Proceedings, NOLCOS’Ol, St-Petersburg, Russia,
June
2001, 1515 (2001).
J.
de Halleux and
G.
Bastin, Stabilization of Saint-Venant equations using
Riemann invariants: Application to waterways with mobile spillways, in CD-
Rom Proceedings, Barcelona, Spain, July
(2002).
J.
de Halleux,
C.
Prieur, J.-M. Coron, B. d’Andrka-Novel and
G.
Bastin
Boundary feedback control in networks of open channels, Preprint,
(2002).
J.-L. Lions, Contr8labilitk Exacte, Perturbations et Stabilisation de Systkmes
Distribugs, Vol.
I,
Masson,
(1988).
D. L. Russell, Controllability and stabilizability theory for linear partial dif-
ferential equations, Recent progress and open questions,
SIAM
Rev.
20,
639
(1978).
E.
Zuazua, Exact controllability for the semilinear wave equation,
J.
Math.
Pures et Appl.
69,
1
(1990).
I. Lasiecka and
R.
Triggiani, Exact controllability of semilinear abstract sys-
tems with applications to waves and plates boundary control problems,
Appl.
Math. Optim.
23,
109 (1991).
M. Cirini, Boundary controllability of nonlinear hyperbolic systems,
SIAM
J.
Control Opt.
7,
198 (1969).
M. Cirini, Nonlinear hyperbolic problems with solutions on preassigned sets,
Michigan Math.
J.
17,
193 (1970).
T.
T.
LI, Exact boundary controllability of unsteady flows in
a
network
of
open canals, to appear in Mathematische Nachrichten.
T. T.
LI and
Y.
JIN, Semi-glabal
C1
solution to the mixed initial-boundary
value problem for quasilinear hyperbolic systems,
Chin. Ann. Math.
22B,
325 (2001).
T.
T.
LI, B.
P.
Rao and
Y.
JIN, Solution
C1
semi-globale et contrdabilit6
exacte frontikre de systkmes hyperboliques quasi linkaires,
C.
R.
Acad. Sci.
Paris,
t.
333
Skrie
I,
219 (2001).
T.
T.
LI and B.
P.
Rao, Exact boundary controllability for quasilinear hy-
perbolic systems,
SIAM
J.
Control Optim.
41,
1748 (2003).
T.
T.
LI and B. P.
Raq
Local exact boundary controllability for
a
class of
quasilinear hyperbolic systems,
Chin. Ann: Math.
23B,
209 (2002).
19.
T. T.
LI, Exact controllability for quasilinear hyperbolic systems and its ap-
plication to unsteady flows in
a
network
of
open canals,
to
appear in Math-
ematical Methods in the Applied Sciences.

HIERARCHY OF PARTIAL DIFFERENTIAL EQUATIONS
AND FUNDAMENTAL SOLUTIONS ASSOCIATED WITH
SUMMABLE FORMAL SOLUTIONS OF A PARTIAL
DIFFERENTIAL EQUATION
OF
NON KOWALEVSKI TYPE
MASATAKE MIYAKE AND KUNIO ICHINOBE
GRADUATE SCHOOL
OF
MATHEMATICS, NAGOYA UNIVERSITY
1.
Introduction
Let
p
and
q
be natural numbers such that
q
>
p,
and consider the following
Cauchy problem in two dimensional complex planes:
a;u(t,
x)
=
a,pu(t,
x),
t,
3:
E
c,
u(0,x)
=
v(x)
E
O,,
qu(0,x)
=
0
(1
5
j
<
P),
(CP)
{
where
Ox(=
C{x})
denotes the set of holomorphic functions in a neighbor-
hood of the origin
x
=
0
or the set of convergent series in
x.
The Cauchy
problem (CP) has a unique formal solution
6(t,
x)
given by
which is divergent in general by the assumption that
q
>
p.
Here the
symbol
O,[[t]],
(a
>
0)
denotes the set of formal power series
f(t,x)
=
C;=,
fn(x)tn (fn(x)
E
0,)
such that
where
I?(.)
denotes the Gamma function, and
go
is called the formal Bore1
transformation of order
a
(in the variable
t).
A
formal power series
f(t,
x)
E
O,[[t]],
is
called a formal power series of Gevrey order
a.
The following questions are natural ones for divergent formal solution
6(t,
x)
of Gevrey type:
[Ql]
When is 7-Gevrey summable for the formal solution
6(t,
x)?
The
definition of Gevrey summability will be given in the following section.
330

331
[Q2]
When
[Ql]
is established, we want to know the integral representa-
tion of the 7-Gevrey sum by using a kernel function which we call the
fundamental solution.
In the case of
(p,
q)
=
(1,2),
i.e., the case of the complex heat equation,
the answers to these questions are obtained completely in a paper by
D.
Lutz, M. Miyake and
R.
Schafkeg in
1999.
For
our
Cauchy problem (CP)
in this paper,
[Ql]
was solved by M. MiyakelO, and
[Q2]
was solved by
K.
Ichinobe'. Moreover,
K.
Ichinobe7 extended those results for equations with
quasi homogeneity. We have to mention that W. Balser obtained sufficient
conditions to the question
[Ql]
for general equations in two dimensional
complex planes with constant
coefficient^^^^^^^^^^.
In this sense, there are no problems to the above questions, but we shall
consider
a
further question as follows:
[Q3]
When the Cauchy data
p(z)
is an entire function of finite exponential
order, the Gevrey order
of
the formal solution
O(t,
z)
becomes smaller than
that in
(1).
Now
a
question arises that how about the answers to the above
questions in this case.
In order to explain our problem, let
us
define a class Exp(r;
C)
(r
>
0)
Exp(r;
C)
=
{f(z)
E
O(C)
;
lf(z)I
I
Cexp(61z1') for
'C,
36
>
0},
(3)
where
O(C)
denotes the set of entire functions. By an easy calculation, we
see that
of entire functions by
u(z)
E
Exp(r;
C)
Iu(~)(O)I
I
CK"(n!)l-l",
(4)
for all
n
E
N
:=
{0,1,2,.
. .
}
by some positive constants
C
and
K.
From
this, we easily see that if we choose
p(z)
E
Exp(r;
C)
for the Cauchy data,
then we have
Since we are interested in the divergent formal solution, we restrict our
4
study to the case
r>-
We further assume that the Cauchy data
p(z)
belongs to a class of entire
functions scaled by exponentially growth as follows.
4-P'
p(z)
E
Exp
(%;
C)
,
0
I
C
I
q
-
p
-
1,
(t
E
N).
(6)
