Inversin R. Allen Micro-hydropower Sourcebook

Подождите немного. Документ загружается.

Lsn

Feb Mar

Apr May

Jun

Jul

Auu

Sep

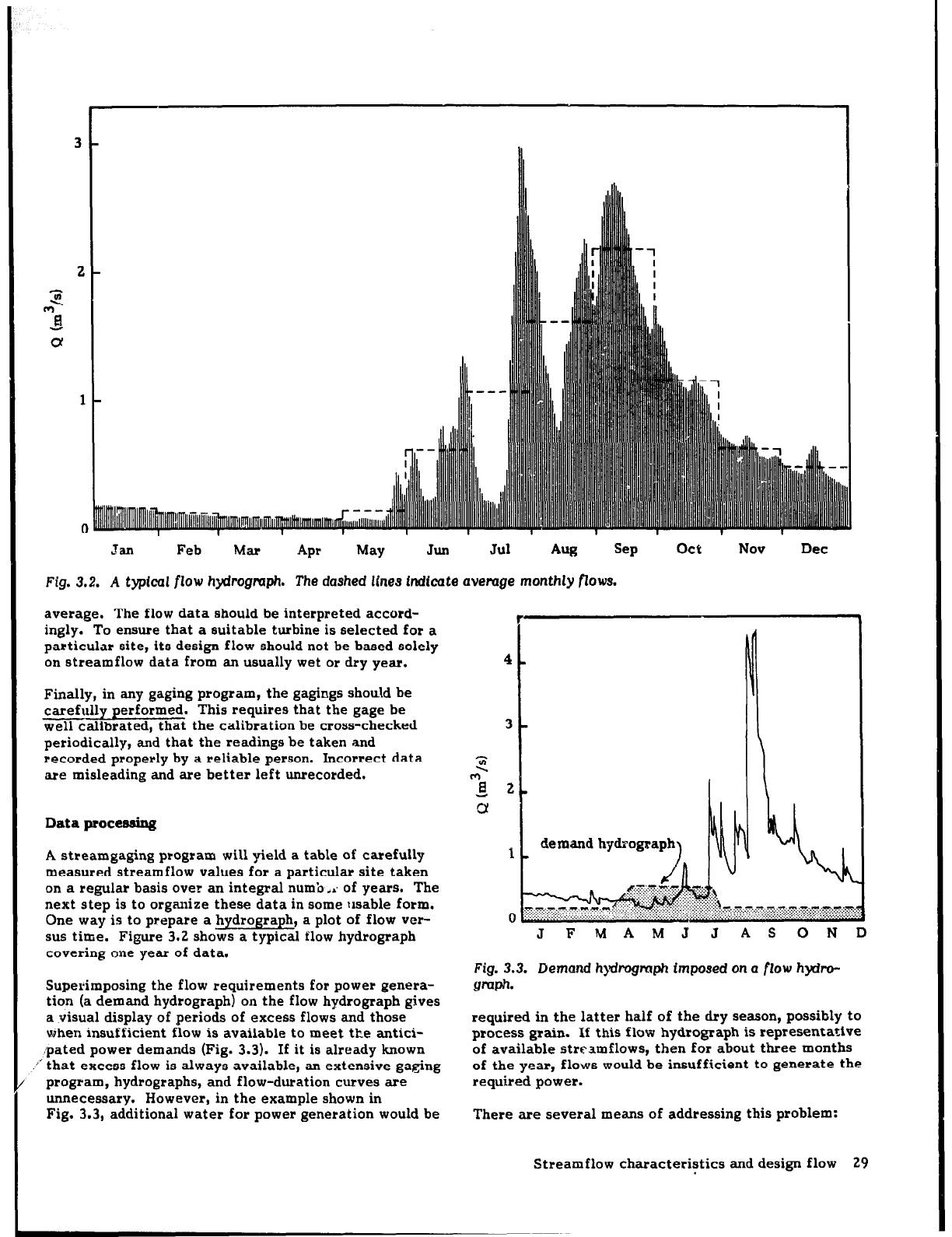
Fig. 3.2. A typIca flow hydrogmph. The dashed lines in&ate average monthly flows.

Nov

Dee

average.

The flow data should be interpreted accord-

ingly. To ensure that a suitable turbine is selected for a

particular site, its design flow should not be based solely

on streamflow data from an usually wet or dry year.

Finally, in any gaging program, the gagings should be

carefully performed. This requires that the gage be

well calibrated, that the calibration be cross-checked

periodically, &d that the readings be taken and

recorded properly by a reliable person. Incorrect data

are misleading and are better left unrecorded.

Data processing

A streamgaging program will yield a table of carefully

measured streamflow values for a particular site taken

on a reelar basis over an integral numb +A, of years. The

next step is to organize these data in some usable form.

One way is to prepare a hydrograph, a plot of flow ver-

sus time. Figure 3.2 shows a typical flow hydrograph

covering one year of data.

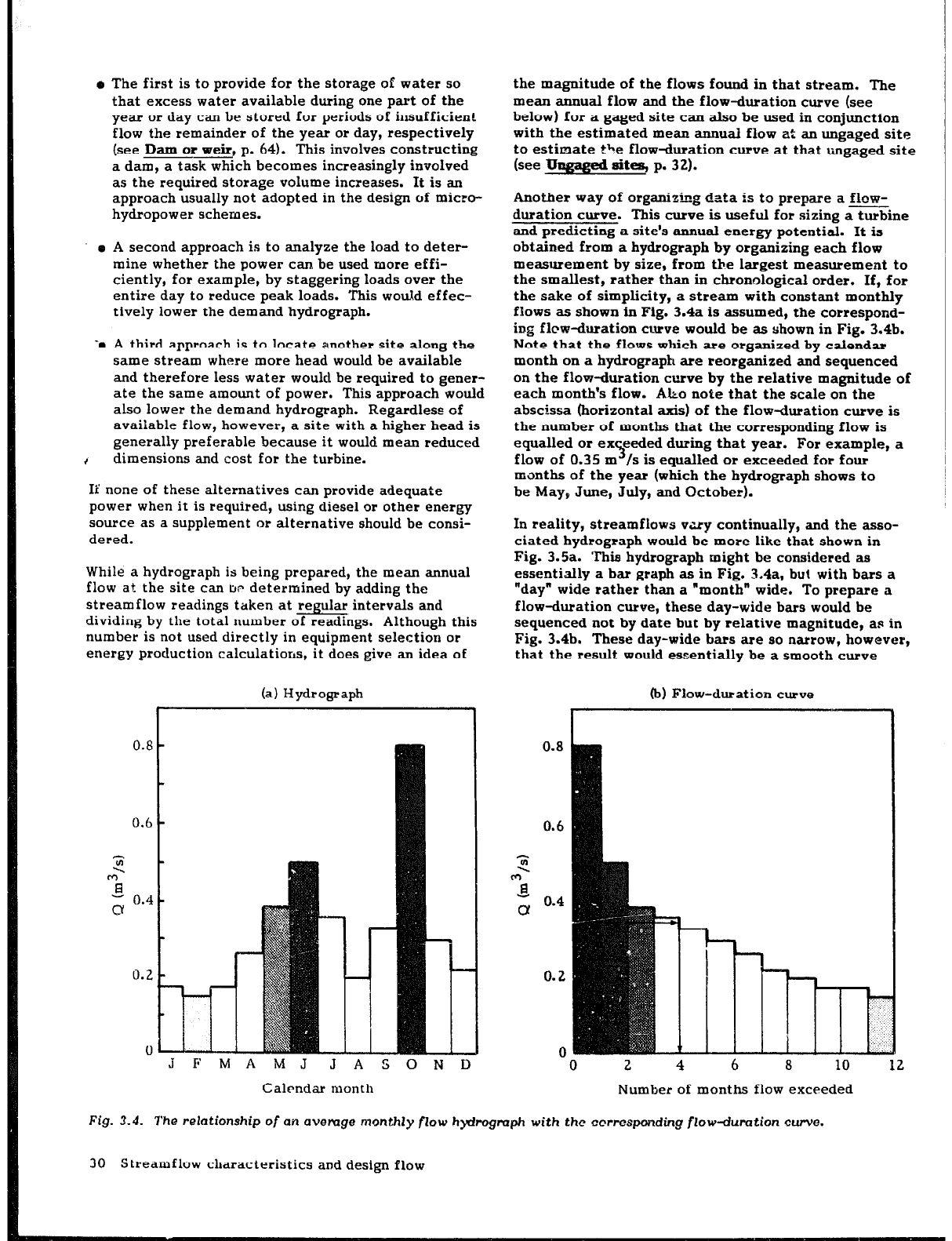
Superimposing the flow requirements for power genera-

tion (a demand hydrograph) on the flow hydrograph gives

a Visual display of periods of excess flows and those

when insufficient flow is available to meet the antici-

!pated power demands (Fig. 3.3). If it is already known

.>‘that excess flow is always available, an extensive gaging

program, hydrographs, and flow-duration curves are

unnecessary. However, in the example shown in

Fig. 3.3, additional water for power generation would be

-2

$ 2

demand bjdrograph

M J J

S 0 N

Fig. 3.3. Demand

hyfrogmph imposed on a flow hyiro-

gmph.

required in the latter half of the dry season, possibly to

process grain.

If this flow hydrograph is representative

of available strcsmflows, then for about three months

of the year, flows would be insufficient to generate the

required power.

There are several means of addressing this problem:

Streamflow characteristics and design flow 29

e The first is to provide for the storage of water so

that excess water available during one part of the

year or day can be stored for periods of insufficient

flow the remainder of the year or day, respectively

(see Dam or weir, p. 64). This involves constructing

a dam,staskch becomes increasingly involved

as the required storage volume increases. It is an

approach usually not adopted in the design of micro-

hydropower schemes.

e A second approach is to analyze the load to deter-

mine whether the power can be used more effi-

ciently, for example, by staggering loads over the

entire day to reduce peak loads. This would effec-

tively lower the demand hydrograph.

‘o A third approach is to locate another site along the

same stream where more head would be available

and therefore less water would be required to gener-

ate the same amount of power. This approach would

also lower the demand hydrograph. Regardless of

available flow, however, a site with a higher head is

generally preferable because it would mean reduced

dimensions and cost for the turbine.

If none of these alternatives can provide adequate

power when it is required, using diesel or other energy

source as a supplement or alternative should be consi-

dered.

While a hydrograph is being prepared, the mean annual

flow at the site can DC determined by adding the

streamflow readings taken at regular intervals and

dividing by the total number of readings. Although this

number is not used directly in equipment selection or

energy production calculations, it does give an idea of

(a) Hydrograph

the magnitude of the flows found in that stream. The

mean annual flow and the flow-duration curve (see

below) for a gaged site can also be used in conjunction

with the estimated mean annual flow

an ungaged site

to estimate the flow-duration curve at that unnaned site

(see &gaged

sites,

p. 32).

Another way of organizing data is to prepare a flow-

duration curve. This curve is useful for sizing a turbine

and predicting a site’s annual energv potential. It is

obt&ed from a hydrograph by or&izing each flow

measurement by size, from the largest measurement to

the smallest, rather than in chronological order. If, for

the sake of simplicity, a stream with constant monthly

flows as shown in Fig. 3.4a is assumed, the correspond-

ing flew-duration curve would be as shown in Fig. 3.4b.

Note that the flows which are organized by calendar

month on a hydrograph are reorganized and sequenced

on the flow-duration curve by the relative magnitude of

each month’s flow. Ako note that the scale on the

abscissa (horizontal axis) of the flow-duration curve is

the number of months that the corresponding flow is

equalled or excieeded during that year. For example, a

flow of 0.35 m /s is equalled or exceeded for four

months of the year (which the hydrograph shows to

be May, June, July, and October).

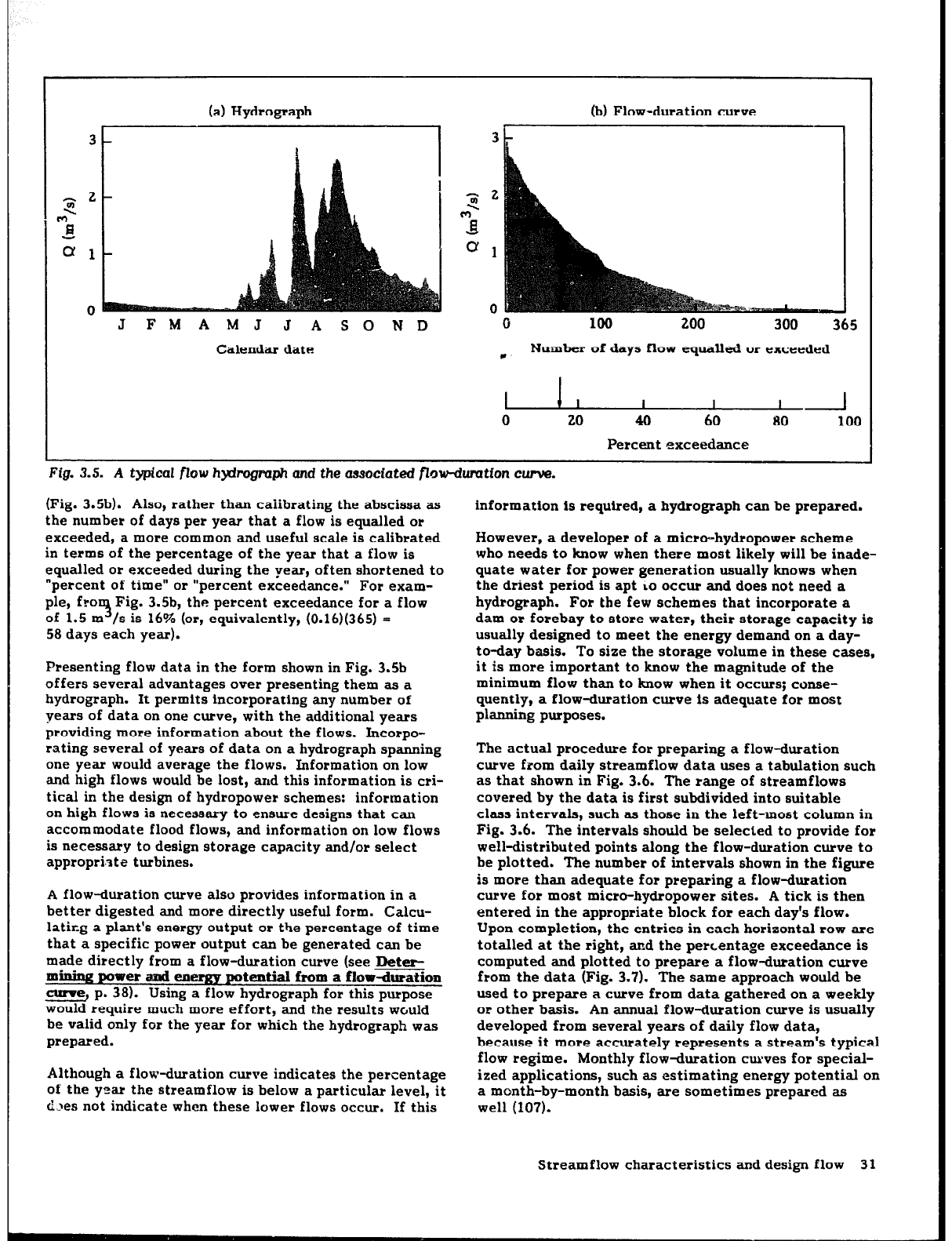
In reality, streamflows vary continually, and the asso-

ciated hydrograph would be mo:e like that shown in

Fig. 3.5a. This hydrograph might be considered as

essentially a bar graph as in Fig. 3.4a, but with bars a

“day” wide rather than a “month” wide. To prepare a

flow-duration curve, these day-wide bars would be

sequenced not by date but by relative magnitude, as in

Fig. 3.4b. These day-wide bars are so narow, however,

that the result would essentially be a smooth curve

(b) Flow-duration curve

0.8

0.6

J F M

AMJ J

A S 0 N

Calrndar month

0.8

2 4

6 8

10 12

Number of months flow exceeded

Fig. 3.4. The relationship of an avemge monthly flow hydmgmph with

the

corresponding flow-duration curve.

30 Streamflow characteristics and design flow

(a) Hydrograph

(b) Flow-duration curve

JFMAMJJASOND

100 200

300

365

Calendar date

Number of days flow equalled or exceeded

LA---,

0 20

60 80

100

Percent exceedance

-- . . _^ - .

_ _- - ._

(Fig. 3.5b). Also, rather than calibrating the abscissa as

the number of days per year that a flow is equalled or

exceeded, a more common and useful scale is calibrated

in terms of the percentage of the year that a flow is

equalled or exceeded during the year, often shortened to

“percent of time” or “percent exceedance.” For exam-

ple, fro

Fig. 3.5b, the percent exceedance for a flow

of 1.5 m

/s is 16% (or, equivalently, (0.16)(365) =

58 days each year).

Presenting flow data in the form shown in Fig. 3.5b

offers several advantages over presenting them as a

hydrograph. It permits incorporating any numbet of

years of data on one curve, with the additional years

providing more information about the flows. Incotpo-

rating several of years of data on a hydtograph spanning

one year would average the flows. Information on low

and high flows would be lost, and this information is cri-

tical in the design of hydropower schemes: information

on high flows is necessary to ensure designs that can

accommodate flood flows, and information on low flows

is necessary to design storage capacity and/or select

appropri,ate turbines.

A flow-duration curve also provides information in a

better digested and mote directly useful form. Calcu-

lating a plant’s energy output or the percentage of time

that a specific power output can be generated can be

made directly from a flow-duration curve (see

Deter-

* .

mm poWW ad energy potential from a flow&Zion

curve, p. 38). Using a flow hydtograph for this purpose

would requite much more effort, and the results would

be valid only for the year for which the hydtograph was

prepared.

Although a flow-duration curve indicates the percentage

of the year the streamflow is below a particular level, it

d>es not indicate when these lower flows occur. If this

who needs to know when there most likely will be inade-

quate water for power generation usually knows when

the driest period is apt LO occur and does not need a

hydrograph. For the few schemes that incorporate a

dam or forebay to

store

water, their storage capacity is

usually designed to meet the energy demand on a day-

to-day basis. To size the storage volume in these cases,

it is more important to know the magnitude of the

minimum flow than to know when it occurs; conse-

quently, a flow-duration curve is adequate for most

planning purposes.

The actual procedure for preparing a flow-duration

curve from daily streamflow data uses a tabulation such

as that shown in Fig. 3.6. The range of streamflows

covered by the data is first subdivided into suitable

class intervals, such as those in the left-most column in

Fig. 3.6. The intervals should be selected to provide for

well-distributed points along the flow-duration curve to

be plotted. The number of intervals shown in the figure

is mote than adequate for preparing a flow-duration

curve for most micro-hydropower sites. A tick is then

entered in the appropriate block for each day’s flow.

Upon completion, the entries in each horizontal tow are

totalled at the tight, and the percentage exceedance is

computed and plotted to prepare a flow-duration curve

from the data (Fig. 3.7). The same approach would be

used to prepare a curve from data gathered on a weekly

ot other basis. An annual flow-duration curve is usually

developed from several years of daily flow data,

because it more accurately represents a stream’s typical

flow regime. Monthly flow-duration curves for special-

ized applications, such as estimating energy potential on

a month-by-month basis, are sometimes prepared as

well (107).

Streamflow characteristics and design flow

Stream

discharge

(m3/s)

10.0

7.00

5.00

4.00

3.00

Number of days that discharge is in

increment begirmirlg with value at left

Ott

Nov

Dee Jan Feb Mar Apr

May June July Aug Sept T~:al

Period during which

discharged at left is

equalled or exceeded

Days

/ 0.3

a 5.5

5. P

a.4

4% i&P

5.2

/La

4.3

c?d

J&J

36d

100

Fig. 3.6.

Sample worksheet for calculating

an annual flow dumtion curve for

a single year.

In the first section below, Estimating mean annual flow

(p. 331, three approaches to estimating the mean annual

40 60 80

100

flow at a site--the numerical average of flows through-

out a year-will be described. The estimates derived

ungaged sites

Most potential micro-hydropower sites are ungaged, and

any gaging8 necessary to prepare an annual hydrogtaph

or flow-duration curve would require at least one year.

For larger hydropower projects, where designs are opti-

mized to maximize return on investment, at least five

to ten years of gaging are required before a project is

undertaken. If meterological data suggest that the pet-

iod of record is drier than usual, additional years of gag-

ing may be requited. Fortunately, for micto-hydro-

power plants which are not designed to maximize power

potential, some knowledge of streamflow patterns may

be useful, but exhaustive study and high accuracy are

unnecessaty.

Percent exceedance

Fig. 3.7.

flow-duration

curve representing the data [n

the

sampie

worksheet (Figure 3.6).

can give an indication whether the flow at the proposed

site seems adequate for hydropower generation. Under

some circumstances, this may be the only flow parame-

32 Streamflow characteristics and design flow

ter that can be aDDroximated with any accuracy; with-

_ -

out a gaging station in the vicinity, no simple technique

exists for accurately estimating the flow-duration curve

for an ungaged stream.

For the larger part of the year, the flow in any stream

will be less than the mean annual flow, because high

flows-one component in calculating the average--are

more above the average than low flows are below it.

Although the mean annual flow gives an idea of a

stream’s power potential, the streamflow is usually less

than this for 50%-70% of the year (60%-70% for areas

with pronounced wet and dry seasons). Therefore, if

design power is to be available for a significant portion

of the year, the flow diverted for hydropower genera-

tion should be somewhat less than mean annual flow.

How much less can be determined only with a firmer

knowledge of the stream’s flow regime, as obtained

from a flow-duration curve.

If the flow required for power generation is on the order

of the mean annual flow in the stream or greater, it is

also necessary to estimate the magnitude of the mini-

mum flow. As briefly described in the second section

below, Estimating minimum flow (p. 37), this is one of

the most difficult estimates to make. However, this

information is needed to determine the maximum power

that a run-of-river plant can generate during the peak

of the dry season or the capacity of a storage reservoir

if more power than this is periodically required.

The third section, Estimating a flow-duration curve

(p. 38), describes a simple approach for approximating a

flow-duration curve for an ungaged st2ea.m. This

approach uses an estimate of the mean annual flow of

that stream and a flow-duration curve developed for a

gaged site in the vicinity. It also presents a method for

deriving a flow-duration curve even if the stream is only

partially gaged and no data on its drainage area, mean

annual flow, or runoff are available.

The estimates of flow made by the simple approaches

discussed in the following sections are approximate and

valid only insofar as the assumptions hold for a particu-

lar situation. More involved methods, such as that

described by Crawford and Thurin in Hydrologic Esti-

mates for Small Hydroelectric Projects (3?), use data on

monthly rainfall on the watershed and monthly potential

evapotranspiration, as well as watershed characteris-

tics-soil-moisture storage level, fraction of runoff that

flows along subsurface paths, and an index of the time

for this flow to enter the stream. The calculations for

these methods can be programmed on a hand calculator;

however, these data often are not available, and if

estimates have to be made, the results of a rather time-

consuming effort may be no more accurate than results

obtained by the much simpler approaches discussed in

Estimating a flow-duration curve (p. 38). However,

these approaches assume the availability of a flow-dura-

tion curve for a nearby gaged site. If none is available,

the flow-duration curve for an ungaged site would have

to be synthesized using a more involved method such as

the one just described, and the data not readily avail-

able would have to be estimated as carefully as possible.

E&mating mean annual flow

Several approaches for estimating the mean annual flow

at an ungaged site are described in the following para-

graphs:

The first approach assumes that there are no gaged

sites in the vicinity and uses runoff information from

maps for the region, country, or continent and the

size of the drainage area associated with the

ungaged site.

The second approach assumes that a gaged site

exists relatively near the ungaged site, either on the

same stream or in a neighboring catchment, and that

a map is available to determine the drainage area of

each catchment.

For cases where no information-runoff, drainage

area, rainfall, etc

.-is available at the ungaged site

but a gaged site exists not too far away, a third

approach requires a series of on-site visits to gather

some flow data.

Although the first two approaches do not require site

visits, such visits to investigate the characteristics of

both the gaged and the proposed catchment are

extremely useful in refining conclusions on the char-

acteristics of streamflows in the ungaged basin. If more

than one approach can be used to determine the mean

annual flow at an ungaged site, each should be used.

Comparing the results will give an indication of the con-

sistency of the estimates.

Even though the approaches for estimating mean annual

flow may not be precise, the values obtained can still

help identify which streams to consider when prospect-

ing for an appropriate site to develop. By knowing how

much flow each square kilometer of catchment contri-

butes to mean annual flow-the specific mean annual

flow-it is possible to estimate the size of a catchment

necessary for a given flow. For example, assume that

each sq are kilometer of catchment contributes

0.050 m /s to the mean annual flow and that typical

heads in the area are about 20 m. To generate 40 kW,

the power e

uation [Eq.(4.3)1 indicates that a flow of

about 0.4 m

/s would be required. Consequently, any

stream to be tapped should have a drainage area of

about 0.4/0.050 or 8 km2 to permit 40 kW to be gener-

ated from the mean annual flow. To generate this

power year-round, an area several times larger would

probably be necessary to ensure adequate flow during

the dry season. Trying to implement such a scheme on a

stream with a drainage area of 5 km’, for example,

should not even be considered unless significantly more

head can be found in the vicinity.

Using runoff data. This approach does not require that

a gaged site be located in the vicinity of a site for

which a micro-hydropower plant is being proposed. It

goes back to basic principles and uses generalized

information on streamflow which is available on a coun-

trywide or continentwide basis.

Streamflow characteristics and design flow

Because the flow in a stream originates in rainfall, rain-

fall data provide a good indication of streamflow. For

example, if an average of 1000 mm or 1.0 m of rain falls

over a specific area each year, then over each square

kilometer of that area, the total volume of water inter-

cepted each year would be

(1.0 m/yr)(l.O km21 = (1.0 m/yr)(106 m2)

= lo6 m3/yr

If all this rainwater ran off into a str

am this one

% 3

square kilometer would contribute 10

m to the

streamflow each year. To convert this

a more mean-

ingful figure, this square kilometer would contribute an

average of

14 $ !&fhl (&&I

= 0.032 m3/s

or 32 I/s to the streamflow over the year.

However, not all rainfall finds its way into a stream.

Some returns directly to the atmosphere through evapo-

ration; some might filter into the ground, where part of

it may eventually flow elsewhere. The rainfall which

actually does enter the stream as either surface or sub-

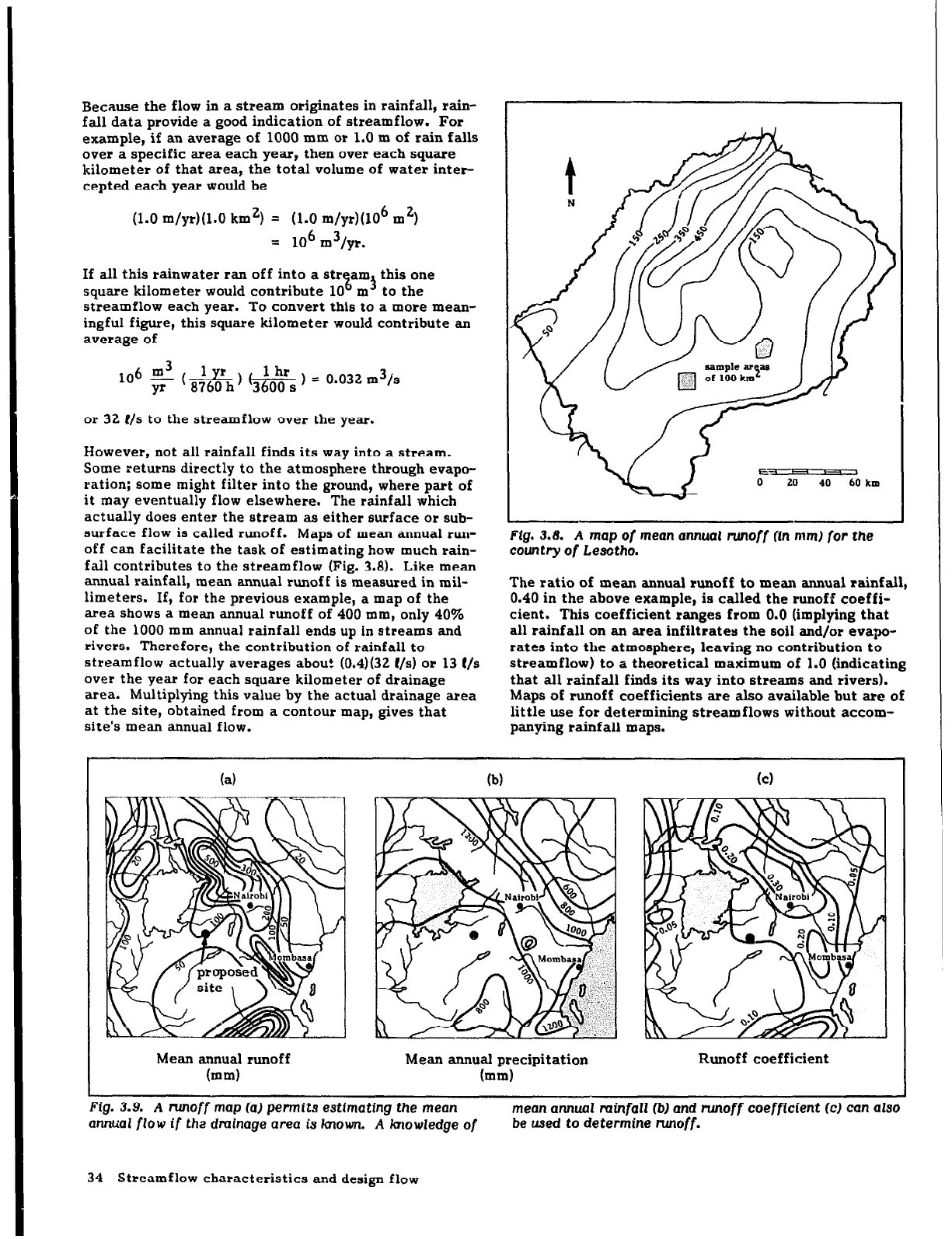
surface flow is called runoff. Maps of mean annual run-

off can facilitate the task of estimating how much rain-

fall contributes to the streamflow (Fig. 3.8). Like mean

annual rainfall, mean annual runoff is measured in mil-

limeters. If, for the previous example, a map of the

area shows a mean annual runoff of 400 mm, only 40%

of the 1000 mm annual rainfall ends up in streams and

rivers. Therefore, the contribution of rainfall to

streamflow actually averages about (0.4)(32 f/s) or 13 l/s

over the year for each square kilometer of drainage

area. Multiplying this value by the actual drainage area

at the site, obtained from a contour map, gives that

site’s mean annual flow.

E-

60 km

Fig. 3.8. A map of mean annual runoff (in mm) for the

country of Lesatho.

The ratio of mean annual runoff to mean annual rainfall,

0.40 in the above example, is called the runoff coeffi-

cient. This coefficient ranges from 0.0 (implying that

all rainfall on an area infiltrates the soil and/or evapo-

rates into the atmosphere, leaving no contribution to

streamflow) to a theoretical maximum of 1.0 (indicating

that all rainfall finds its way into streams and rivers).

Maps of runoff coefficients are also available but are of

little use for determining streamflows witkout accom-

panying rainfall maps.

(a) (bl

Mean annual runoff

(mm)

Mean annual precipitation

(mm)

Runoff coefficient

rig. 3.~. A

nmoyf map (a)

permlrs

esttmatlng tne mean

mean annual minfall (0) and

runoff

coefftcient (c) can also

annual flow

thz dmlnage area

is known.

A knowledge

be used

determine runoff.

34 Streamflow characteristics and design flow

As the preceding discussion shows, one method of esti-

mating mean annual flow requires a contour map and a

mean annual runoff map of the area. Instead of a mean

annual runoff map, a map of mean annual rainfall

together with a map of runoff coefficients can be used.

In this case, the mean annual runoff for the area would

be estimated by multiplying its mean annual rainfall by

the appropriate runoff coefficient. For example, if a

site is proposed in the location shown in Fig. 3.9a, then

the mean annual runoff averaged over the basin would

be about 100 mm/yr. If the drainage area $as been

measured from a contour map to be 42 km , then the

mean annual flow at this site would be

If only information on rainfall (Fig. 3.9b) and runoff

coefficient (Fig. 3.9~) is known, the mean annual runoff

can still be determined as

(920

mm&r) (0.11) = 100 mm/yr.

mean

annual

rainfall

runoff

coefficient

m&n

annual

runoff

This value would then be used to determine mean annual

flow as just shown. The two values of mean annual run-

off cannot be expected to agree precisely because

(100

mm/y4 (

errors

are incurred in both plotting these maps and

interpolating between lines.

‘iii: $ifrn2 )(42

km2) = 0.13 m3/s

conversion

drainage

Fig. 3.10 makes

several

points about the use of runoff

mean

maps or data from nearby catchment basins to calculate

annual factor area

EUlIUd

a site’s mean annual flow. In this figure, lines of con-

runoff

flow

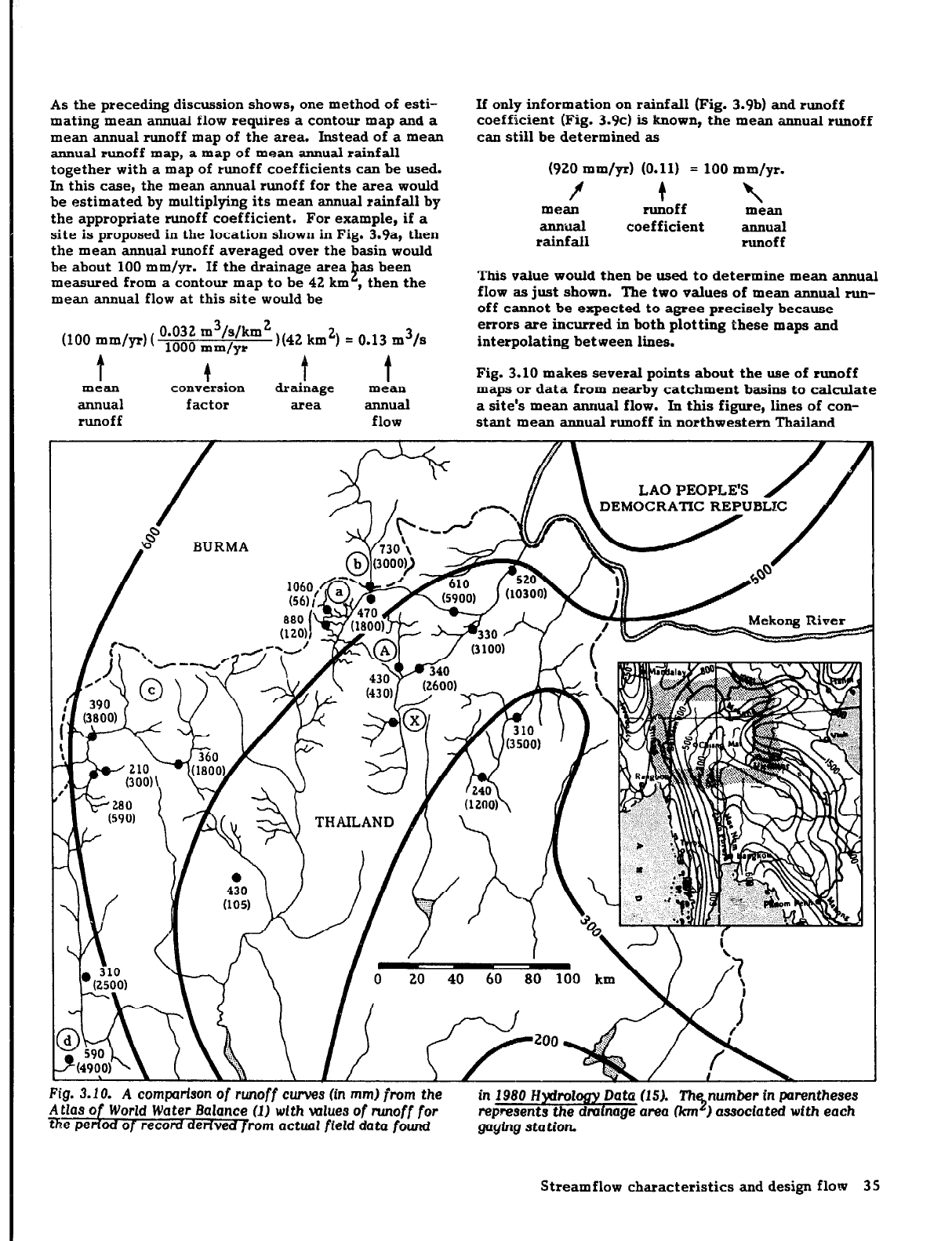
stant mean annual runoff in northwestern Thailand

Fig. 3.10. A comparison of

runoff curves

(in

mm) from

the

Atlas of

World Water Balance (1) with walues of runoff

for

%e pefTW of recoti derivedfrom actual ffeld data four&

1980 Hydrology Data (15). Th%number

parentheses

represents

the dminage area Ikm 1 associated

with each

gciging station.

Streamflow characteristics and design flow 35

found on a small-scale runoff map of Asia (1) (see insert

in Fig. 3.10) were carefully transposed onto a larger

scale map of the area. Also superimposed in Fig. 3.10

are values of mean annual runoff for the period of

record calculated at gaging stations in the region-mean

annual flow at each gaging station divided by the asso-

ciated drainage area--to permit crosschecking values of

runoff that can be estimated by using the runoff

contours. Several conclusions can be drawn in this case:

Mean annual runoff for small basins, such as basin (a)

with a runoff of 1060 mm and an area of only

56 km2, may vary significantly from that which

might be estimated using either runoff contours or

data from nearby sites with large,catchments.

The river runoff at a site along a river is determined

by the areal average of runoff

over

its associated

drainage area, n,.,i by the value of runoff at that site

itself. The value of runoff which makes its way

down to site (b), for example, is significantly larger

than the runoff at that point-about 500 mm-

because the large catchment stretches a consider-

able distance to the north into a region of larger

runoff.

In the region at the left (c), actual values of runoff

are consistently about half of what the runoff map

would predict. The runoff contours in this region

appear to have been incorrectly drawn if the gaged

values are assumed correct. When site& that area

aTe developed, the gaged values rather than those

from the runoff map should probably be used as a

guide. However, the actual runoffs in the area (d)

and farther south agree fairly closely with the values

from the map.

Fig. 3.10 illustrates the degree of agreement, or dis-

agreement, between the values of runoff taken from a

small-scale runoff map and the actual values derived

from gagings. A value of mean annual flow derived

using only contours from that map clearly is only an

estimate. In scaling up a runoff map about 20-fold, as

was done for Fig. 3.10, errors may be introduced. In

addition, the scale of the map may not permit local var-

iations to be taken into consideration. Furthermore, in

preparing the runoff maps appearing in the Atlas of

World Water Balance (l), various “indirect” methods

were used to determine runoff for irsufficiently gaged

regions, and further errors may have been introduced at

that level. National maps of runoff, such as that shown

in Fig. 3.8, can provide more accurate results and, if not

available, should be prepared, especially if a broader

small-hydropower program is to be undertaken in a

country.

As an example of how to predict the mean annual flow

from the runoff data shown in Fig. 3.10, assume that the

mean annual flow for the stream at an ungaged site X in

that figure in northwestern Thailand has to be esti-

mated. From a contour map, the catchment

?!i

ea asso-

ciated with this site is measured to be 260 km . To

determine runoff, either a mean annual runoff map or

countrywide data can be used. If only a runoff map is

available the runof woul

400 mm

be estimated at about

0; m$s/km’.

Since its area was deter-

mined to be 26 km , the mean annual flow at site X

would be 3.4 m 1s. On the other hand, assuming that a

runoff map had been prepared for the region based on

local data, the runoff from the proposed catchment

would have been estimated as closer to 340 mm or

0.011 m3/s/km2.

This would correspond to a mean

annual flow of 2.9 m3/s. The precision with which run-

off data can be predicted at the ungaged site can be

seen to significantly influence the accuracy of the final

estimate.

Uadng ratio of area& This approach assumes that,

although a runoff map of the area is not available, a

gaged site does exist in the vicinity. It further assumes

that the catchment basin for a proposed micro-hydro-

power site displays characteristics-topography, land

use, geomorphology, lithology, etc.-similar to those of

a gaged site in the vicinity, on either the same stream

or one in a neighboring catchment.

If, in addition to the above, the precipitation over the

basins is similar, the runoff for both catchments would

be of the same magnitude, and the mean annual flow

would then be approximately proportional to drainage

area. The mean annual flow at the proposed site can

then be estimated by simply multiplying the mean

annual flow at the gaged site by the ratio of the drain-

age area at the ungaged to that at the gaged site.

Returning to the previous example, assume that there is

a gaged site A in the vicinity of site X. With the

assumptions made9 the mean

-2 3

ual flow t the pro-

posed site will average (260 km )/(430 km ) = 0.60 or

60% of the corresponding flow at the gaged site. Since

a mean annual flow for the gaged site A of 5.7 m3/s can

be calculated from records over the period 1974-82, the

mean annual flow at the ungaged site can be predicted

10.60)(5.7) = 3.4 m3/s

If more than two gaged sites are located in the vicinity,

the validity of the initial assumption-that mean annual

flow is well correlated with drainage area-can be

determined.

If the two catchment basins display similar characteris-

tics as described above but rainfall differs, this factor

can be taken into consideration. This can be accom-

plished by multiplying the mean annual flow estimated

by the approach described above by the ratio of the

mean annual precipitation over the ungaged basin to

that over the gaged basin. An areal average of precipi-

tation over each basin should be used if the necessary

information is available.

Correlating flows. If the drainage area at the ungaged

site in unknown and cannot be determined by using

available maps, the previous approaches cannot be used.

The approach described in this section requires a gaged

site not too distant from the ungaged site. Although no

knowledge of the size of the drainage area is required,

36 Streamflow cb,aracteristics and design flow

this approach requires a series of site visits to make

occasional streamflow measurements. These visits need

not be made on a regular basis, but they should be

spread out over a year so that high, average, and low

flows can be measured. If time is critical, a short-term

correlation can be used; for example, the site could be

gaged every few days for a month. Such short-term

correlations are best made when flows are close to

mean annual flow; extremely wet or dry periods should

be avoided. Each day that a flow measurement is made,

the flow at the gaged site should also be obtained. Each

set of flow readings is plotted on log-log paper, with

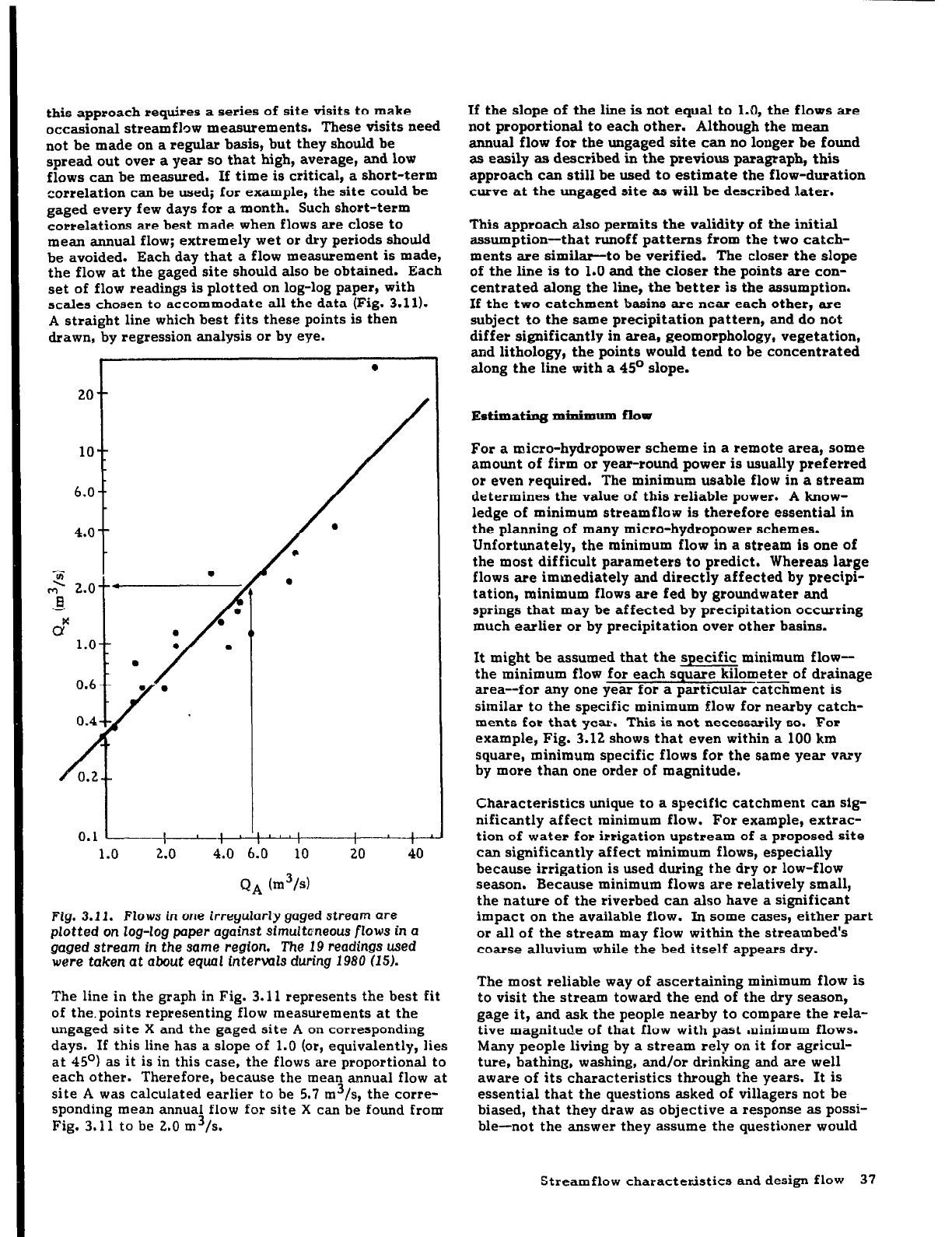
scales chosen to accommodate all the data (Fig. 3.11).

A straight line which best fits these points is then

drawn, by regression analysis or by eye.

6.0

1.0

0.6

Y l

o’llD+

4.0

I (

0 10

QA (m3/s)

Fig. 3.11. Flows in one irregularly gaged stream

are

plotted

log-log

paper

against simultaneous flows

in a

gaged

stream

the

same region. The 19

readings used

were taken

at about

equal intervals

during 1980

(151.

The line in the graph in Fig. 3.11 represents the best fit

of the.points representing flow measurements at the

ungaged site X and the gaged site A

corresponding

days. If this line has a slope of 1.0 (or, equivalently, lies

at 45O) as it is in this case, the flows are proportional to

each other. Therefore, because the mean annual flow at

site A was calculated earlier to be 5.7 m3/s, the corre-

sponding mean annual flow for site X can be found from

Fig. 3.11 to be 2.0 m3/s.

If the slope of the line is not equal to 1.0, the flows are

not proportional to each other. Although the mean

annual flow for the ungaged site can no longer be found

as easily as described in the previous paragraph, this

approach can still be used to estimate the flow-duration

curve at the ungaged site as will be described later.

This approach also permits the validity of the initial

assumption-that runoff patterns from the two catch-

ments are similar-to be verified. The closer the slope

of the line is to 1.0 and the closer the points are con-

centrated along the line, the better is the assumption.

If the two catchment basins are near each other, are

subject to the same precipitation pattern, and do not

differ significantly in area, geomorphology, vegetation,

and lithology, the points would tend to be concentrated

along the line with a 4S” slope.

Estimating minimum flow

For a micro-hydropower scheme in a remote area, some

amount of firm or year-round power is usually preferred

or even required. The minimum usable flow in a stream

determines the value of this reliable power. A know-

ledge of minimum streamflow is therefore essential in

the planning of many micro-hydropower schemes.

Unfortunately, the minimum flow in a stream is one of

the most difficult parameters

predict. Whereas large

flows are immediately and directly affected by precipi-

tation, minimum flows are fed by groundwater and

springs that may be affected by precipitation occurring

much earlier or by precipitation over other basins.

It might be assumed that the specific minimum flow-

the minimum flow for each square kilometer of drainage

area--for any one year for a particular catchment is

similar to the specific minimum flow for nearby catch-

ments for that year. This is not necessarily so. For

example, Fig. 3.12 shows that even within a 100 km

square, minimum specific flows for the same year vary

by more than one order of magnitude.

Characteristics unique to a specific catchment can sig-

nificantly affect minimum flow. For example, extrac-

tion of water for irrigation upstream of a proposed site

can significantly affect minimum flows, especially

because irrigation is used during the dry or low-flow

season. Because minimum flows are relatively small,

the nature of the riverbed can also have a significant

impact on the available flow. In some cases, either part

or all of the stream may flow within the streambed’s

coarse alluvium while the bed itself appears dry.

The most reliable way of ascertaining minimum flow is

to visit the stream toward the end of the dry season,

gage it, and ask the people nearby to compare the rela-

tive magnitude of that flow with past .ninimum flows.

Many people living by a stream rely on it for agricul-

ture, bathing, washing, and/or drinking and are well

aware of its characteristics through the years. It is

essential that the questions asked of villagers not be

biased, that they draw as objective a response as possi-

ble-not the answer they assume the questioner would

Streamflow characteristics and design flow

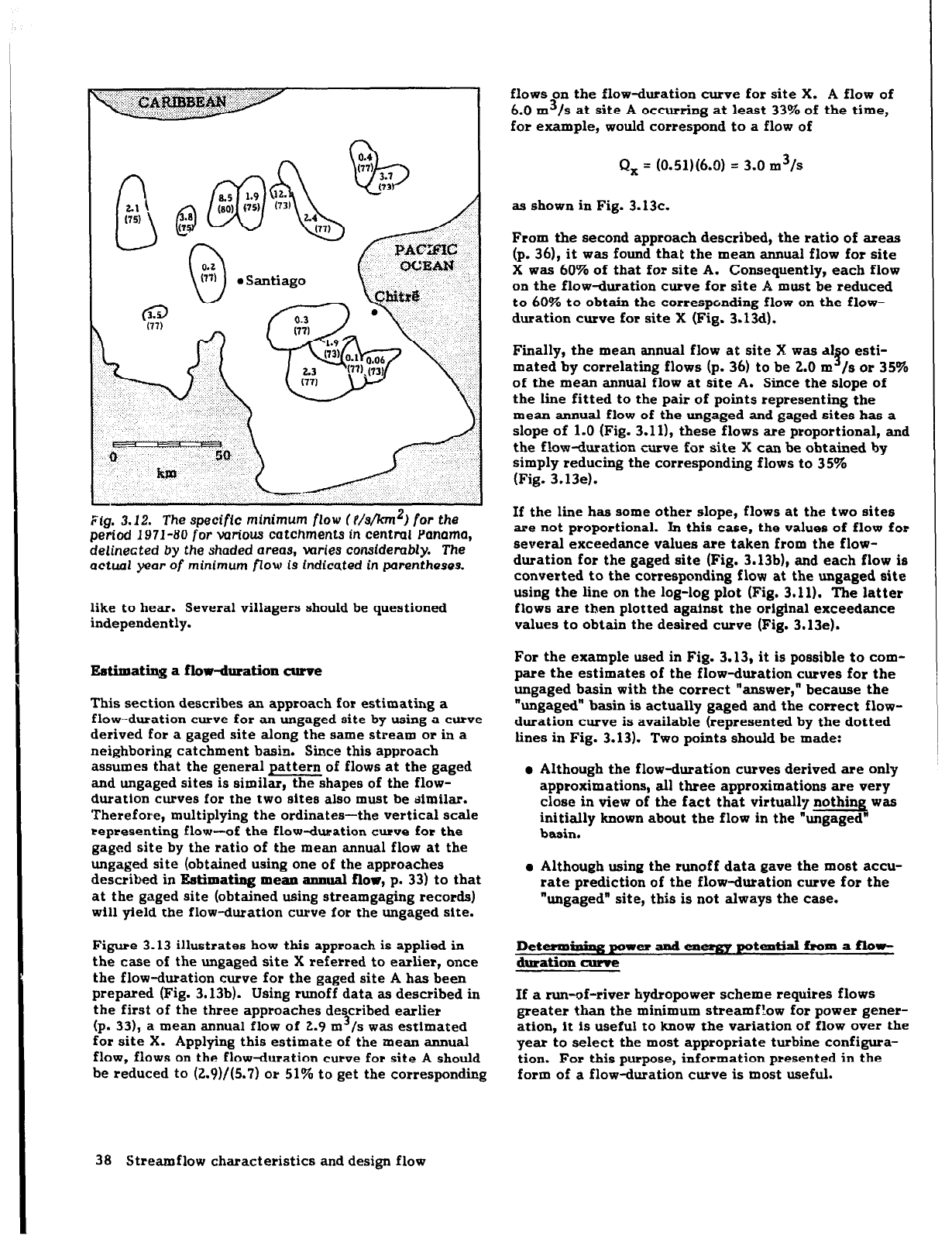
r’Lg. 3.12. The specific minimum

flow CPki/km2) for

the

period 1971-80

for

various catchments in central Punama,

delinected

the shaded areas,

varies

considerably. The

actual year of

minimum flow ts fndicsted in parentheses.

like to hear. Several villagers should be questioned

independently.

Estimating a flow-duration curve

This section describes an approach for estimating a

flow-duration curve for an ungaged site by using a curve

derived for a gaged site along the same stream or in a

neighboring catchment basin. Since this approach

assumes that the general pattern of flows at the gaged

and ungaged sites is similar, the shapes of the flow-

duration curves for the two sites also must be similar.

Therefore, multiplying the ordinates-the vertical scale

representing flow-of the flow-duration curve for the

gaged site by the ratio of the mean annual flow at the

ungaged site (obtained using one of the approaches

described in Estimating

mean

axmnal flow, p. 33) to that

at the gaged site (obtained using streamgaging records)

will yield the flow-duration curve for the ungaged site.

Figure 3.13 illustrates how this approach is applied in

the case of the ungaged site X referred to earlier, once

the flow-duration curve for the gaged site A has been

prepared (Fig. 3.13b). Using runoff data as described in

the first of the three approaches de

cribed earlier

(p. 33), a mean annual flow of 2.9 m

/s was estimated

for site X. Applying this estimate of the mean annual

flow, flows on the flow-duration curve for site A should

be reduced to (2.9)/(5.7) or 51% to get the corresponding

flows on the flow-duration curve for site X. A flow of

6.0 m”/s at site A occurring at least 33% of the time,

for example, would correspond to a flow of

Q, = (0.51)(6.0) = 3.0 m3/s

as shown in Fig. 3.13~.

From the second approach described, the ratio of areas

(p. 36), it was found that the

mean

annual flow for site

X was 60% of that for site A. Consequently, each flow

on the flow-duration curve for site A must be reduced

to 60% to obtain the corresponding flow on the flow-

duration curve for site X (Fig. 3.13d).

Finally, the mean annual flow at site X was al

mated by correlating flows (p. 36) to be 2.0 m

o esti-

/s or 35%

of the mean annual flow at site A. Since the slope of

the lie fitted to the pair of points representing the

mean annual flow of the ungaged and gaged sites has a

slope of 1.0 (Fig. 3.11), these flows are proportional, and

the flow-duration curve for site X can be obtained by

simply reducing the corresponding flows to 35%

(Fig. 3.13e).

If the line has some other slope, flows at the two sites

are not proportional. In this case, the values of flow for

several exceedance values are taken

from

the flow-

duration for the gaged site (Fig. 3.13b), and each flow is

converted to the corresponding flow at the ungaged site

using the line on the log-log plot (Fig. 3.11). The latter

flows are then plotted against the original exceedance

values to obtain the desired curve (Fig. 3.13e).

For the example used in Fig. 3.13, it is possible to com-

pare the estimates of the flow-duration curves for the

ungaged basin with the correct “answer,” because the

“ungaged” basin is actually gaged and the correct flow-

duration curve is available (represented by the dotted

lines in Fig. 3.13). Two points should be made:

Although the flow-duration curves derived are only

approximations, all three approximations are very

close in view of the fact that virtualbl nothinq was

initially known about the flow in the “~a

basin.

a Although using the runoff data gave the most accu-

rate prediction of the flow-duration curve for the

“ungaged” site, this is not always the case.

Determining power ad energy potential from a flow-

duration curve

If a run-of-river hydropower scheme requires flows

greater than the minimum streamftow for power gener-

ation, it is useful to know the variation of flow over the

year to select the most appropriate turbine configura-

tion. For this purpose, information presented in the

form of a flow-duration curve is most useful.

38 Streamflow characteristics and design flow