James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

6.3 Application to observed steady eddies

189

(b)

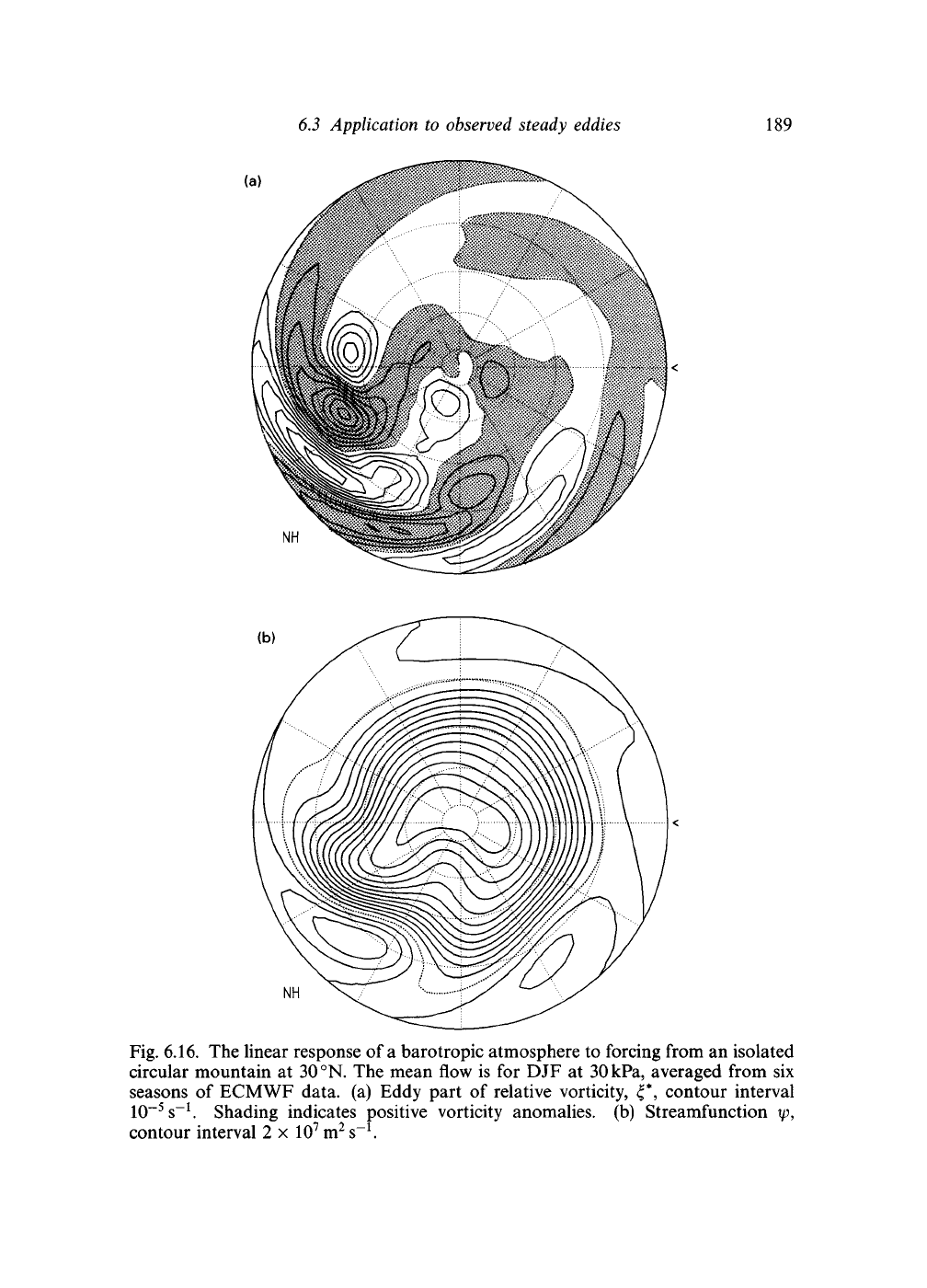
Fig. 6.16. The linear response of a barotropic atmosphere to forcing from an isolated

circular mountain at 30 °N. The mean flow is for DJF at 30 kPa, averaged from six

seasons of ECMWF data, (a) Eddy part of relative vorticity, <**, contour interval

10~

Shading indicates positive vorticity anomalies, (b) Streamfunction xp,

contour interval 2 x 10

190 Wave propagation

and

steady eddies

6.4

Vertical propagation

Rossby waves

The theory in the preceding section can be adapted for the case of vertically

propagating Rossby waves. The results enable us to extend the discussion

of the earlier part of this chapter to a stratified fluid, and are important in

helping to clarify the links between the troposphere and the higher regions of

the atmosphere. These links will be discussed in Chapter 9. Once again, the

approximations made in the theory can easily be criticized. But the simple

analysis has great value in establishing a conceptual framework into which

the results of more realistic, but consequently less accessible, calculations can

be fitted. We will first consider the problem illustrated in Fig. 6.18. An atmo-

sphere is forced by disturbances at its lower boundary; these disturbances

may represent flow over mountain ranges, thermal forcings, or (especially

in the case of the stratosphere) they may represent disturbances in some

lower region of the atmosphere. The problem we will address is whether

these disturbances may influence the flow at great heights above the lower

boundary, or whether their influence is confined to the lowest levels of the

atmospheric layer.

Our starting point will be the quasi-geostrophic potential vorticity equa-

tion. Because a particular application of the results is to the stratosphere

it is convenient to express that equation in log pressure or 'pseudo-height'

coordinates. The pseudo-height is given by z

= Hln(p

/p), where the atmo-

spheric scale height H = RTo/g. The quasi-geostrophic potential vorticity

equation is written:

(6J6)

where p

is the density and N is the Brunt-Vaisala frequency. The density

of an isothermal atmosphere varies as

= p

(6.37)

The analysis will be simplified drastically by assuming that the basic state

consists of constant zonal wind U and Brunt-Vaisala frequency N. These

assumptions can be relaxed, as we shall see later. We partition the stream-

function into zonal mean and eddy parts:

= -Uy +

xp*

(6.38)

where

\\p*\

is supposed to be small compared with \U\. For the present we

will assume that the perturbations are steady. Then the quasi-geostrophic

6.4 Vertical propagation of Rossby waves 191

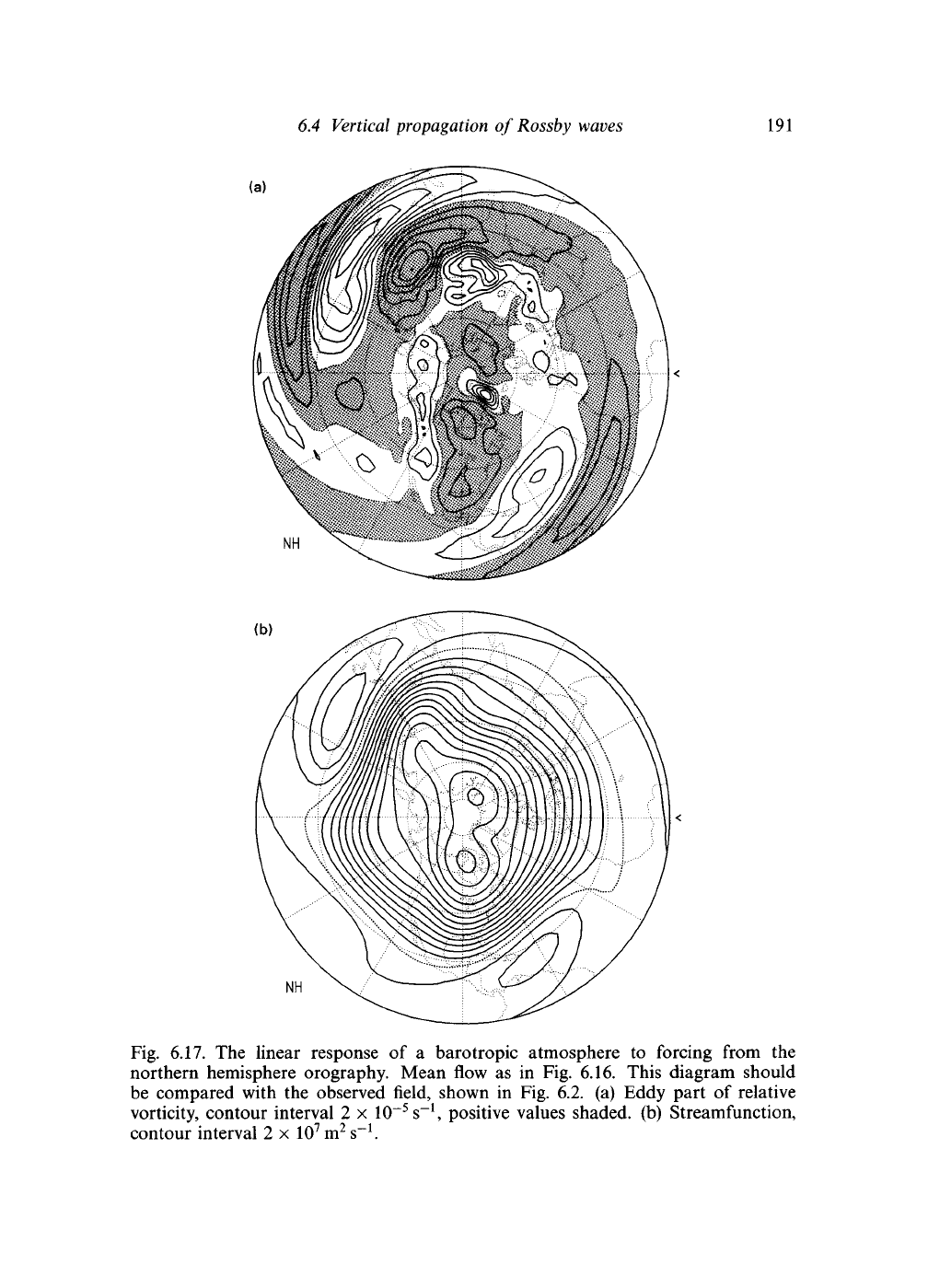
Fig. 6.17. The linear response of a barotropic atmosphere to forcing from the

northern hemisphere orography. Mean flow as in Fig. 6.16. This diagram should

be compared with the observed field, shown in Fig. 6.2. (a) Eddy part of relative

vorticity, contour interval 2 x 10~

, positive values shaded, (b) Streamfunction,

contour interval 2 x

192

Wave propagation and steady eddies

Forcing, wavenumber k

Fig. 6.18. Schematic illustration

the problem

to be

discussed

this section.

potential vorticity equation can

linearized

give:

U-

dz'\N

(6.39)

The forcing

the lower boundary

supposed

to be

wavelike; then we seek

wavelike solutions

the form:

ip*

¥(z')e

/2H

i{kx+ly

(6.40)

The factor exp(z'/2H)

introduced

account

for the

decrease

density

with height. An upward propagating wave must have an increasing amplitude

with height

if its

wave activity

is to

remain constant. Substitution

this

form

solution into Eq. (6.39) yields

equation

for

the amplitude *F:

'dz

l2+

(6.41)

in the

preceding section,

the

total wavenumber

K is

given

by K =

For

the

stratosphere,

typically

4 x

10~

and the

temperature

around

220

Thus

the

scale height

H is

6.4

km,

and the

term

f/(2NH)

corresponds to zonal wavenumber 2 in the midlatitudes. Clearly, for negative

6.4 Vertical propagation of Rossby waves 193

U or for large positive 17, the coefficient of

is negative, but otherwise it is

positive.

These two cases have quite different types of solution. When the coefficient

is positive, the amplitude relation, Eq. (6.41), may be written:

¥ = 0, (6.42)

where

4{S£T-

Equation (6.42) is a wave equation with solutions:

¥(z') = AJ™' + BQ-

imz

' (6.44)

and m plays the role of a vertical wavenumber. The constants of integration

A and B are determined from the condition that the group velocity is

upwards, as assumed in Fig. 6.18. Then B = 0 and A = *Fo is determined by

the amplitude of the forcing. The disturbance is vertically propagating and

is given by the expression:

That is, the amplitude increases with height as the density decreases. The

wave action density, however, remains constant. Such wavelike solutions are

favoured for small but positive U or for small total wavenumber K.

In the alternative case, the amplitude equation may be written:

^--^ = 0, (6.46)

with

This has the general solution:

+Btr»

\ (6.48)

so that \i plays the role of an e-folding height. Note that if a boundary

condition of no forcing is applied at z' —• oo, then ,4 = 0. The constant

B is simply determined by the lower boundary condition, that is, by the

forcing imposed at z

= 0. The amplitude of the wave may either increase

or decrease with height, according to whether ji~

is larger or smaller than

2H,

but the wave action always decreases with height. These evanescent

194 Wave propagation

and

steady eddies

evanescent

i i

-20

evanescent

propagating

40 60

zonal wind

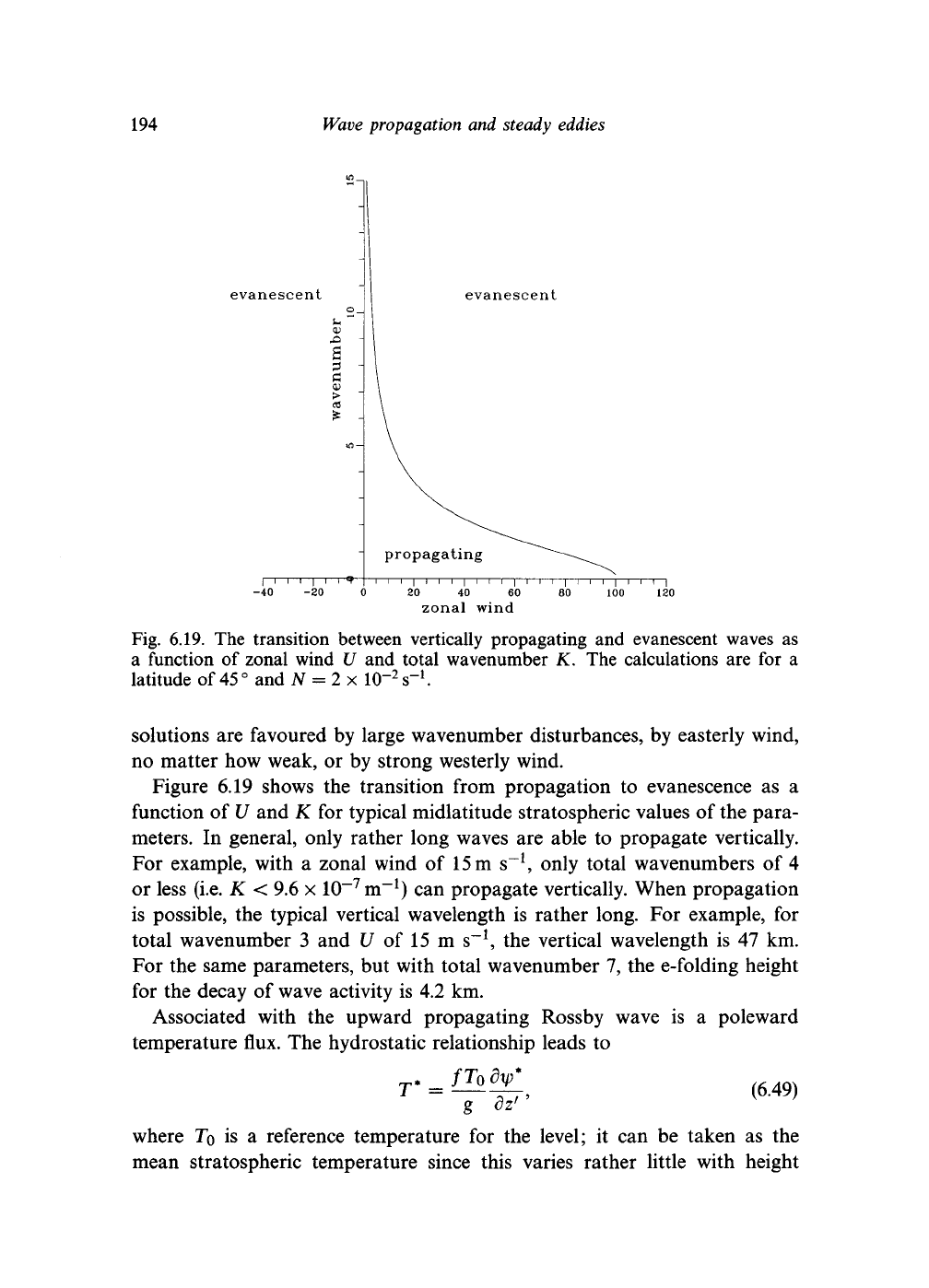
Fig.

6.19. The

transition between vertically propagating

and

evanescent waves

a function

zonal wind

U and

total wavenumber

K. The

calculations

are for a

latitude

and N = 2 x

10"

s""

solutions

are

favoured

large wavenumber disturbances,

easterly wind,

no matter how weak,

or by

strong westerly wind.

Figure

6.19

shows

the

transition from propagation

evanescence

as a

function

U and

K for

typical midlatitude stratospheric values

the para-

meters.

general, only rather long waves

are

able

propagate vertically.

For example, with

zonal wind

15 m

only total wavenumbers

of 4

or less (i.e.

K <

9.6

10~~

)

can

propagate vertically. When propagation

is possible,

the

typical vertical wavelength

rather long.

For

example,

for

total wavenumber

3 and (7 of

m s"

, the

vertical wavelength

is 47 km.

For the same parameters,

but

with total wavenumber 7,

the

e-folding height

for

the

decay

wave activity

4.2

km.

Associated with

the

upward propagating Rossby wave

is a

poleward

temperature flux. The hydrostatic relationship leads

/To

dxp*

(6.49)

where

To is a

reference temperature

for the

level;

it can be

taken

as the

mean stratospheric temperature since this varies rather little with height

6.4 Vertical propagation of Rossby waves 195

in the lower stratosphere. The perturbation streamfunction for a vertically

propagating wave is given by Eq. (6.45), so that the poleward velocity may

be written:

and the temperature perturbation is

f[o^

z'/2H\

I _j_

_|_

i(kx+ly+mz')

(6.51)

Thus the poleward temperature flux is

_ f _L

The first two terms in the brackets are wavelike and their zonal mean is zero;

the third constant term determines the zonal mean poleward temperature

flux, which is

z//

". (6.53)

As we discussed in Section 5.2, the existence of this temperature flux implies

that the upward propagating Rossby wave must show a phase tilt to the

west with height. It is easy to use the same arguments to show that if the

wave is evanescent in z', then

[

T*] =0. (6.54)

In this case, there is no phase tilt, and the troughs and ridges of an evanescent

disturbance will be exactly vertical.

Equation (6.53) is at first sight a curious result. Since this model involves

no vertical wind shear, the mean temperature gradients are zero, and so there

is no energy conversion associated with this flux. In fact, the arguments of

Chapter 4 would show that a meridional circulation would develop; provided

the Rossby waves are linear, steady and there is no dissipation, the zonal

mean heat flux carried by this circulation would exactly balance the eddy

heat flux just calculated.

196 Wave propagation and steady eddies

6.5 The Eliassen-Palm flux

The question of how wave activity propagates in both the vertical and

poleward directions has now been raised. In this section, we shall see that

the propagation of Rossby waves is intimately connected to their interaction

with the basic zonal state, thus confirming a result which has already been

hinted at in the earlier discussions. The arguments of this section are not

restricted simply to the steady disturbances which have been the focus of

our consideration throughout the earlier part of the chapter, but, rather, can

be applied to propagating Rossby waves of any frequency. The theory that

we will develop will bring together the results of Sections 6.2 and 6.3, which

were concerned with horizontal propagation and those of Section 6.4, where

we discussed vertical propagation.

In this general theory, we will begin with the quasi-geostrophic version of

the potential vorticity equation:

where

£%)

56)

and S is a source term which is taken to include all processes such as

heating and friction which can alter the potential vorticity of an element

of air. In the entirely artificial case where Rayleigh friction and Newtonian

cooling are assumed, both with the same time constant

S can be written as

(<le —

Q)/*

<le

being the equilibrium distribution of q corresponding to zero

relative vorticity and radiative equilibrium stratification. But, in general,

it is misleading to regard the effects of friction or cooling simply as the

dissipation of potential vorticity anomalies.

First, we consider the propagation of disturbances by linearizing the

potential vorticity equation about a general zonal flow U(y

z'); denoting the

perturbation potential vorticity by q , the linearized equation is:

-z—h U— h [q]

-z— = S*. (6.57)

The poleward gradient of potential vorticity of the basic state

[q]

is a crucial

parameter. It may be expressed as:

Note that there are three contributions to the potential vorticity gradient.

6.5 The

Eliassen-Palm

flux 197

The first term is simply the poleward gradient of planetary vorticity and

the second the poleward gradient of relative vorticity. The third term is

dominated by (f/N)

U/dz

if the vertical variations of U are signifi-

cant on a scale smaller than the density scale height. The factor (N/f)

serves to determine the natural ratio of horizontal and vertical scales. The

perturbation potential vorticity can be expressed in terms of the geostrophic

streamfunction:

££)

59)

Now assume that the perturbation is wavelike in x, y and z', and has

frequency

so that it may be written:

'-cot)^

(6.60)

Substitution in Eq. (6.57) yields the dispersion relation:

where the source or sink term S* has been dropped. This

justified provided

the frequency and rate of propagation are all fast. The effect of retaining

weak dissipation will be examined later. Equation (6.61) is familiar. When

U is constant and

= 0 (steady waves) it reduces to Eq. (6.47). If vertical

variations of U and p

are dropped, it reduces to Eq. (6.14). The dispersion

relationship enables the group velocity to be calculated, so that the direction

of wave activity propagation can be determined. The poleward component

of group velocity is:

dco

_ 2[q]

kl _ 2[q]

n~ Tp ~Kf~

62)

and the vertical component is:

km 2[q]

63)

8co 2[q]

km 2[q]

—

zrr—TT^

-itr

If a slowly varying approximation were made, these two expressions would

form the basis of three-dimensional ray tracing, analogous to the two-dimens-

ional theory developed in Section 6.2. But for the purposes of interpreting

198

Wave propagation

and

steady eddies

atmospheric data,

need

not

pursue

the

rigorous development

of ray

tracing theory.

may at

this point bring together

the

discussions which

led us to

Eqs.

(6.31) and (6.52). The poleward momentum flux carried by disturbances

of the form given

Eq. (6.60)

simply:

[iiV]

-yPFo|V/

, (6.64)

which

just

the

result derived earlier

but

with possible vertical variations

included.

But

comparison with

Eq.

(6.62) shows that this poleward

mo-

mentum flux can

the poleward group velocity:

-[uV].

(6.65)

Similarly,

the

poleward potential temperature flux:

[v'd*]

^-\W

km (6.66)

(cf. Eq. 6.52) can be

to the

vertical component

of the

group velocity:

From Eqs. (6.65)

and

(6.67), we see that the direction

the vector

F=(-p>V],

f[v*6*]/6

(6.68)

is parallel

to the

local group velocity. The vector

F is

called

the

Eliassen-

Palm flux,

and it is an

important diagnostic.

The

interpretation

of the

Eliassen-Palm flux as measuring group velocity

robust

situations where

group velocity

meaningful. Unlike

ray

tracing,

does

not

rely

on any

assumption about

slowly varying background flow.

But the Eliassen-Palm flux may also

interpreted

other ways.

Let us

return

to the

quasi-geostrophic potential vorticity equation, Eq. (6.55),

and

take

its

zonal average:

[q]t+

[v*q*]

[S]. (6.69)

Consistent with the quasi-geostrophic assumption, the poleward eddy trans-

port

of q is the

only dynamical term

in the

zonal mean equation.

But the

poleward flux

potential vorticity

[v*q*]

to the

Eliassen-Palm

flux. From Eq. (6.59),

follows that:

J IHRJ

R v |

(67Q)