James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

6.5 The

Eliassen-Palm

flux 199

where

the continuity equation

= 0 has been invoked. The last term

can

be simplified by relating v* to 9* using thermal wind balance, so that

Eq.

(6.70) becomes:

}

On taking the zonal averages, the first term, which is a derivative with

respect to x, vanishes, and so we may write:

That is, the modification of the basic state by the eddies is described by

the divergence of the Eliassen-Palm flux. This result is quite general; it

is equally valid for steady or transient disturbances, provided the quasi-

geostrophic approximation can be sustained. The result using pseudo-height

= H ln(p

/p) as the vertical co-ordinate has been given here. An equivalent

result using pressure as the vertical coordinate can easily be derived; in this

case the Eliassen-Palm flux can be written:

} (6.73)

Note that the vertical component has changed sign, consistent with pressure

decreasing upwards. Returning to the linearized potential vorticity equation,

Eq. (6.57), in the form:

(where

friction and diabatic heating are ignored), a further interpretation of

the

Eliassen-Palm flux can be made. Multiply Eq. (6.74) by

q*/[q]

and

take

its zonal average; the result of this manipulation is:

dt \ [q]

)

where the identity Eq. (6.72) has been used. Such a conservation relation is

of great interest. It states that the quantity

= ^?M

(

)

carried by the propagating disturbances, and is conserved. The flux of A

simply the Eliassen-Palm flux. Indeed, A is a fundamental measure of the

vigour

of the waves; it is conserved in a way in which, for example, the eddy

200

Wave propagation and steady eddies

2.0E+15 M3(RA0)

ZOE+20 M3(PA)

LATITUDE

90N

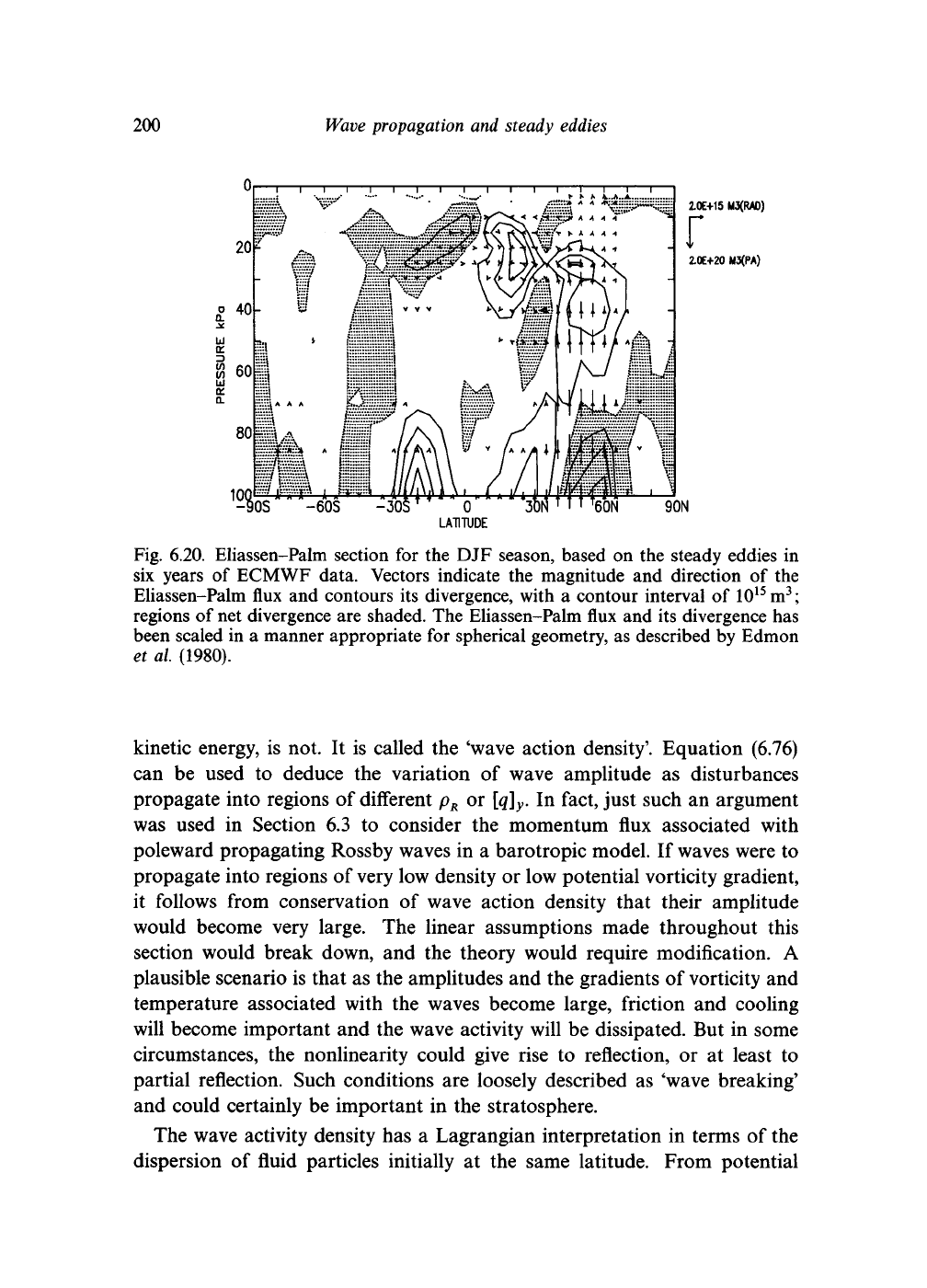
Fig. 6.20. Eliassen-Palm section for the DJF season, based on the steady eddies in

six years of ECMWF data. Vectors indicate the magnitude and direction of the

Eliassen-Palm flux and contours its divergence, with a contour interval of

;

regions of net divergence are shaded. The Eliassen-Palm flux and its divergence has

been scaled in a manner appropriate for spherical geometry, as described by Edmon

et al (1980).

kinetic energy, is not. It is called the 'wave action density'. Equation (6.76)

can be used to deduce the variation of wave amplitude as disturbances

propagate into regions of different p

[q]

In fact, just such an argument

was used in Section 6.3 to consider the momentum flux associated with

poleward propagating Rossby waves in a barotropic model. If waves were to

propagate into regions of very low density or low potential vorticity gradient,

it follows from conservation of wave action density that their amplitude

would become very large. The linear assumptions made throughout this

section would break down, and the theory would require modification. A

plausible scenario is that as the amplitudes and the gradients of vorticity and

temperature associated with the waves become large, friction and cooling

will become important and the wave activity will be dissipated. But in some

circumstances, the nonlinearity could give rise to reflection, or at least to

partial reflection. Such conditions are loosely described as 'wave breaking'

and could certainly be important in the stratosphere.

The wave activity density has a Lagrangian interpretation in terms of the

dispersion of fluid particles initially at the same latitude. From potential

6.6 Eliassen-Paim

fluxes

and barodinic

lifecycles

201

vorticity conservation, the poleward displacement of a fluid element is

n = -q

/lq]y, (6.77)

so that the wave action density is just

(6.78)

That is, the wave action density is proportional to the mean square parcel

displacement.

Bearing in mind these theoretical properties of the Eliassen-Palm flux, it

is of interest to plot both the flux itself and its divergence when studying

the general circulation. A latitude-pressure cross section showing vectors of

F and contours of V

•

F has been advocated as a compact diagnostic of the

propagation of disturbances and their interaction with the zonal mean flow.

The vectors give information about the propagation of the disturbances,

while the divergence gives information about the generation, dissipation and

mean flow interaction of the disturbances.

Figure (6.20) shows such a cross section for the steady waves of the tropo-

sphere. The Eliassen-Palm flux vectors are vertical in the lower troposphere,

but become more horizontal near the tropopause at around 25kPa. They

turn mainly towards the tropics, though some wave activity is seen turning

more polewards and propagating through the tropopause into the strato-

sphere. A partitioning by wavenumber indeed reveals that the shorter waves

contribute to the equatorward flux along the tropopause, while only long

waves continue upwards and polewards into the stratospheric polar night jet.

Convergence of the Eliassen-Palm flux is largest just below the tropopause in

the midlatitudes, indicating that the mean flow is modified in this region by

the effects of the eddies. The large divergence near the surface demonstrates

the generation of steady eddies by various surface forcing processes there.

6.6 Eliassen-Palm fluxes and barodinic lifecycles

Most of this chapter has been concerned with the steady disturbances seen

in the seasonal mean flow, both of the troposphere and of the stratosphere.

A final topic in this chapter is to extend our discussion to the transient

disturbances of the troposphere. The theory of the preceding section can be

applied equally well to propagating transient disturbances; such application

leads to helpful insight into the nature of the nonlinear barodinic lifecycles

described in Section 5.5 and leads to an interpretation of the observed

transient eddy activity in terms of barodinic life cycles.

Consider the two paradigms of linear barodinic instability, the Eady and

202

Wave propagation and steady eddies

(a)

Charney

A * *

A A *

•t'

\ ,

• t

(b)

- Z

-S.I.

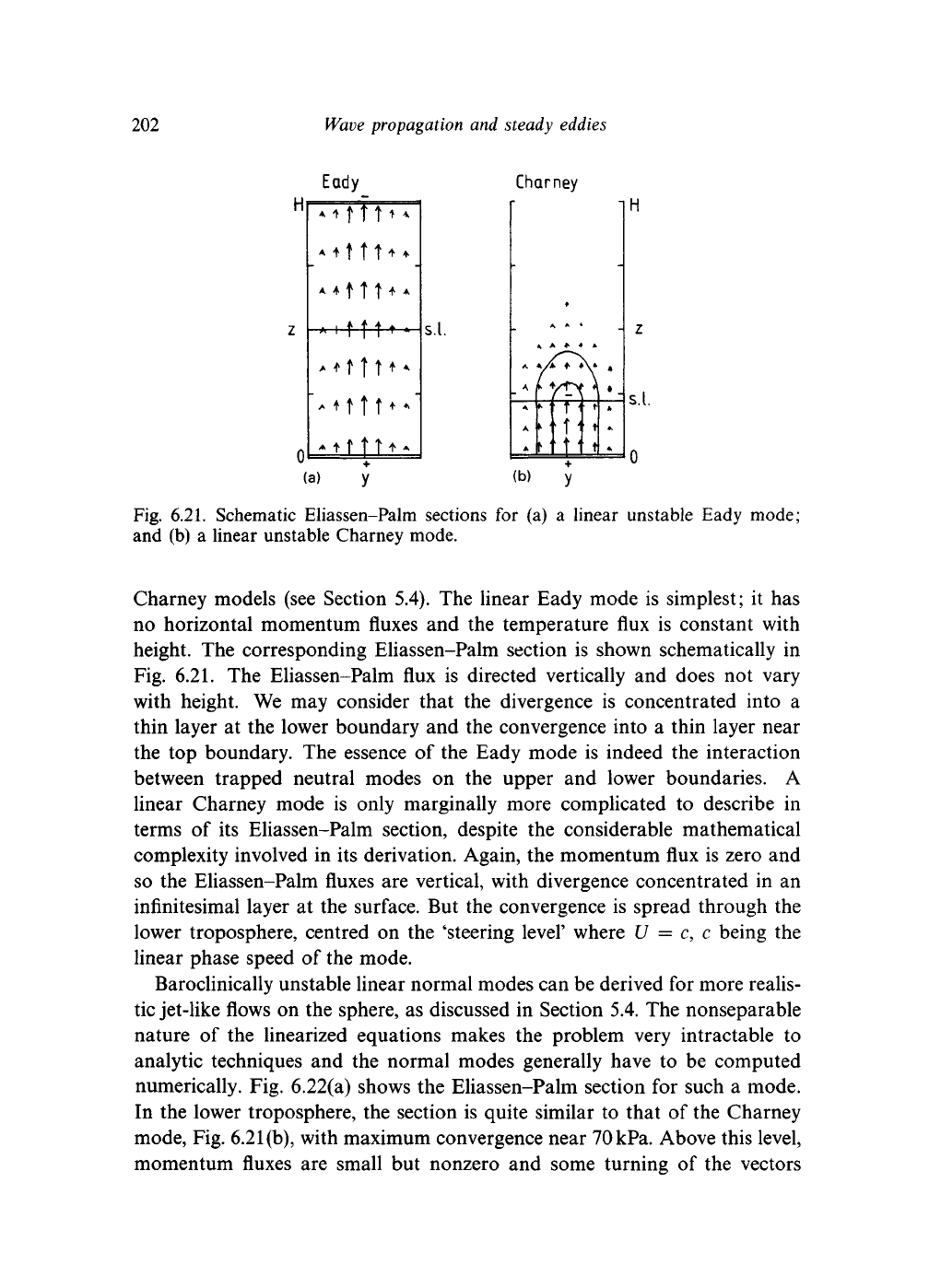
Fig. 6.21. Schematic Eliassen-Palm sections for (a) a linear unstable Eady mode;

and (b) a linear unstable Charney mode.

Charney models (see Section 5.4). The linear Eady mode is simplest; it has

no horizontal momentum fluxes and the temperature flux is constant with

height. The corresponding Eliassen-Palm section is shown schematically in

Fig. 6.21. The Eliassen-Palm flux is directed vertically and does not vary

with height. We may consider that the divergence is concentrated into a

thin layer at the lower boundary and the convergence into a thin layer near

the top boundary. The essence of the Eady mode is indeed the interaction

between trapped neutral modes on the upper and lower boundaries. A

linear Charney mode is only marginally more complicated to describe in

terms of its Eliassen-Palm section, despite the considerable mathematical

complexity involved in its derivation. Again, the momentum flux is zero and

so the Eliassen-Palm fluxes are vertical, with divergence concentrated in an

infinitesimal layer at the surface. But the convergence is spread through the

lower troposphere, centred on the 'steering level' where U = c, c being the

linear phase speed of the mode.

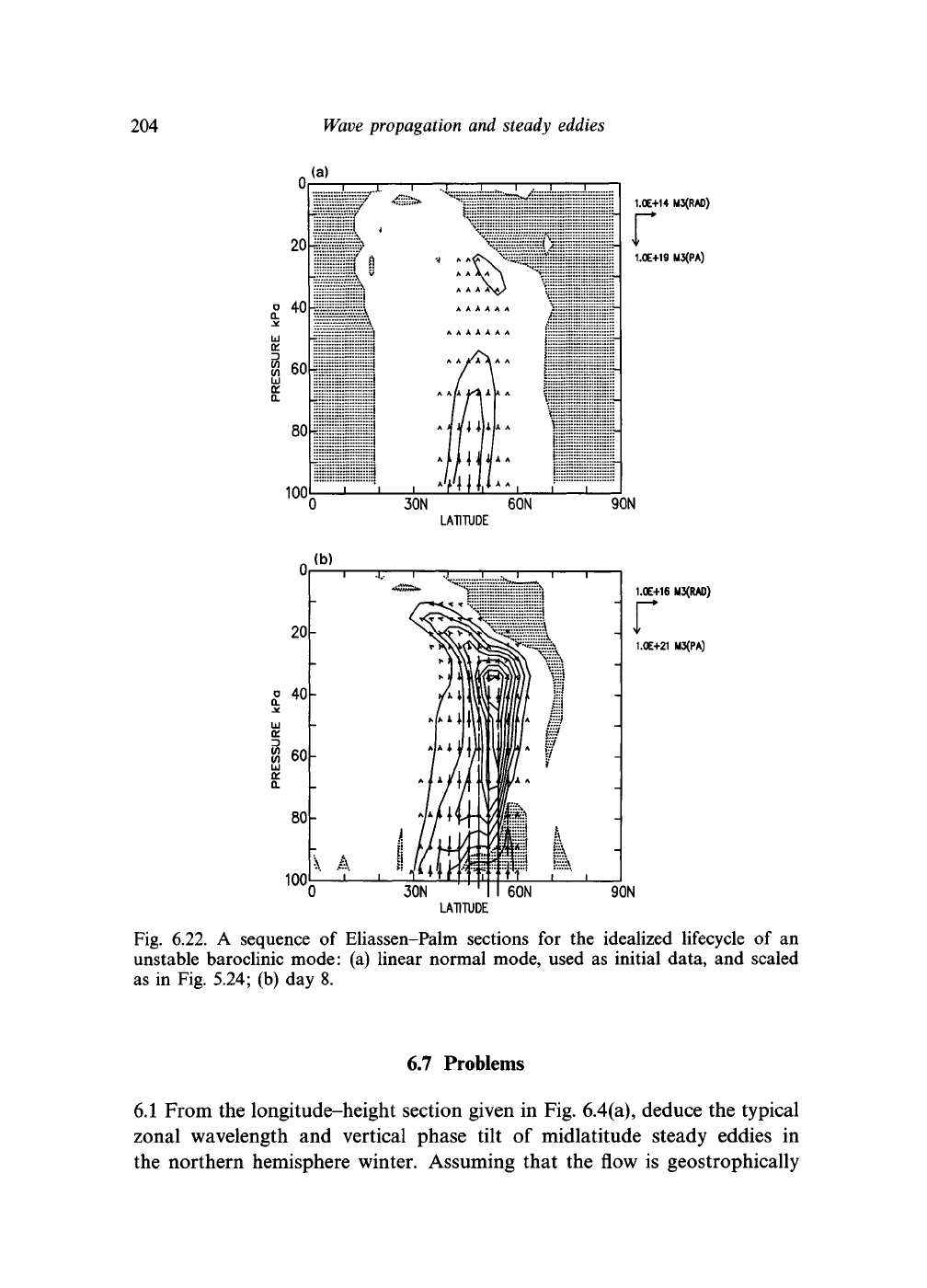
Baroclinically unstable linear normal modes can be derived for more realis-

tic jet-like flows on the sphere, as discussed in Section 5.4. The nonseparable

nature of the linearized equations makes the problem very intractable to

analytic techniques and the normal modes generally have to be computed

numerically. Fig. 6.22(a) shows the Eliassen-Palm section for such a mode.

In the lower troposphere, the section is quite similar to that of the Charney

mode, Fig. 6.21

(b),

with maximum convergence near 70kPa. Above this level,

momentum fluxes are small but nonzero and some turning of the vectors

6.6

Eliassen-Palm

fluxes

and baroclinic lifecycles

203

can be seen. The remainder of the diagram shows Eliassen-Palm sections

from various stages of a lifecycle integration, starting from the linear normal

mode as initial condition. As the wave saturates, the low level fluxes become

smaller, and the maximum wave activity is seen at higher levels. In the

decay phase, large, nearly horizontal vectors are seen near the tropopause;

wave activity is propagating equatorward in the upper troposphere, and is

absorbed before the tropical easterlies are reached. Thus, the baroclinic

lifecycle may be described in terms of linear instability generating wave

activity at low levels in the midlatitudes. This is followed by upward and,

finally, equatorward propagation; at the same time the original seat of the

instability is switched off. Finally, wave activity is dissipated in the subtrop-

ics,

returning energy to the zonal mean flow. This is a typical evolution and

the predominantly equatorward propagation is a ubiquitous feature of such

waves. Anomalous zonal flows can be produced in which the equatorward

propagation is suppressed, and wave activity is focussed towards the pole.

In this case, the rapid collapse of the mature disturbance is not seen, and,

instead, a slowly decaying, nearly circular, system results.

The

final

frame of Fig. 6.22, showing the time mean Eliassen-Palm sections

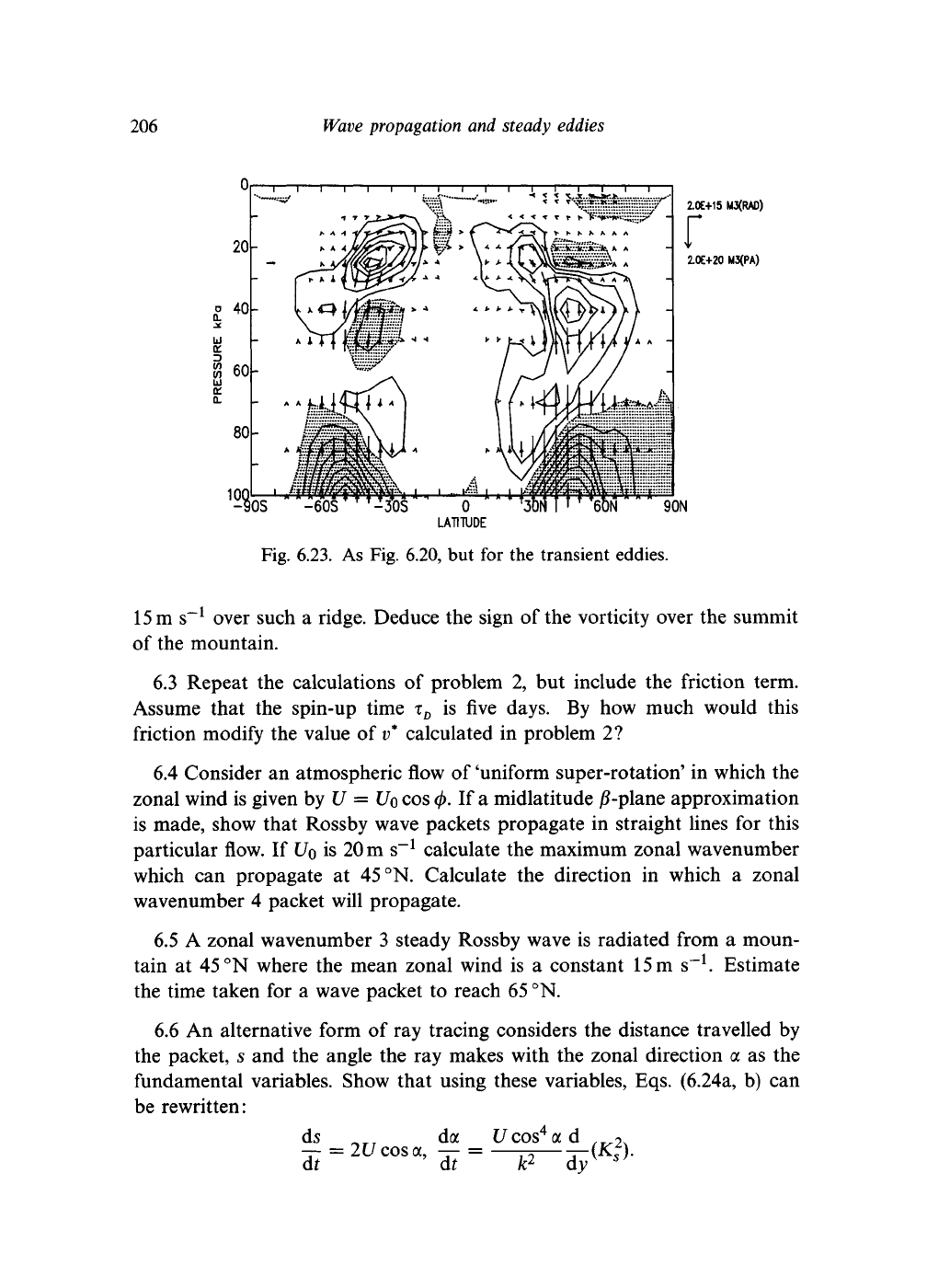
for the entire lifecycle, is remarkably similar to the section shown in Fig. 6.23.

The latter is based on transient temperature and momentum fluxes observed

during the northern hemisphere winter. It shows the same divergence in the

midlatitudes and upward propagation through the midtroposphere as does

the idealized lifecycle calculation. There is the same strong equatorward

propagation along the tropopause towards lower latitudes. In other words,

the pattern of transient wave activity in the troposphere is characteristic of

nonlinear baroclinic lifecycles. The low level temperature fluxes are described

quite well by linear theory, but the momentum fluxes are a feature of the

nonlinear mature and decaying phase of the normal modes.

This chapter has taken as its theme the way in which the troposphere

can support wave propagation of quasi-geostrophic, balanced disturbances.

The insight that such a model gives us helps us to understand many of

the features of the distribution of the steady and transient wave activity of

the middle latitudes. But these interpretations must not be pushed too far;

the assumptions of linearity and slowly varying background states that we

have been forced to make do not hold to any great degree of accuracy. But

our models do give a vocabulary which enables the results of much more

complex, generally numerical calculations to be described.

204

Wave propagation and steady eddies

30N

60N

LATITUDE

100

30N

60N

LATITUDE

90N

Fig. 6.22. A sequence of Eliassen-Palm sections for the idealized lifecycle of an

unstable baroclinic mode: (a) linear normal mode, used as initial data, and scaled

as in Fig. 5.24; (b) day 8.

6.7 Problems

6.1 From the longitude-height section given in Fig. 6.4(a), deduce the typical

zonal wavelength and vertical phase tilt of midlatitude steady eddies in

the northern hemisphere winter. Assuming that the flow is geostrophically

6.7 Problems

205

(c)

40-

LJJ

60-

100

I i

SKJ*—7/77

TITI

5T"

Jfc

T/V

tsuwvv

-r^

yvtw

6a/

fin i

fh+ifh

'- /

jtv'f

[•

30N

60N

LATITUDE

1.QE+16 M3(RAD)

1.0E+21 M3(PA)

90N

(d)

20-

o 40

60-

80-

100

' '--^ '

•

"*/

-"«

"r*"i

» hKAAiriiiy

( AAAAajJiU*/A

AAAAAAiJHlA

A A A

Jr.*

i i^-ki I* 1

A A

V'KXL•***

t #T

A A

Ac*

*•

30N

60N

LATITUDE

1.0E+16 M3(RAD)

1.0E+21 M3(PA)

90N

Fig. 6.22 (cont.). (c) Day 12; and (d) average through from day

to day 15. Contour

interval

for

•

4 x

(a), (b) and (c) and

2 x

(d).

balanced, deduce the typical poleward temperature flux associated with the

steady eddies. Compare your results with observations (see Fig. 6.5(a)).

6.2 Model the Rockies

ridge

1000

km wide (in the zonal direction),

5000

km long (in the meridional direction), 1.5 km high and centred at

°N.

Estimate the poleward eddy velocity

associated with barotropic flow

206

Wave propagation and steady eddies

2.0E+15 M3(RA0)

2.0E+20 M3(PA)

LATITUDE

90N

Fig. 6.23. As Fig. 6.20, but for the transient eddies.

m s"

over such a ridge. Deduce the sign of the vorticity over the summit

of the mountain.

6.3 Repeat the calculations of problem 2, but include the friction term.

Assume that the spin-up time x

is five days. By how much would this

friction modify the value of

calculated in problem 2?

6.4 Consider an atmospheric flow of 'uniform super-rotation' in which the

zonal wind is given by U =

cos

</>.

If a midlatitude /?-plane approximation

is made, show that Rossby wave packets propagate in straight lines for this

particular flow. If Uo is

m s"

calculate the maximum zonal wavenumber

which can propagate at 45 °N. Calculate the direction in which a zonal

wavenumber 4 packet will propagate.

6.5 A zonal wavenumber 3 steady Rossby wave is radiated from a moun-

tain at 45 °N where the mean zonal wind is a constant

m s"

. Estimate

the time taken for a wave packet to reach 65 °N.

6.6 An alternative form of ray tracing considers the distance travelled by

the packet, 5 and the angle the ray makes with the zonal direction a as the

fundamental variables. Show that using these variables, Eqs. (6.24a, b) can

be rewritten:

ds da U cos

a d

— = 2(7 cos a, — = —-5—i-CK

dt dt k

6.7 Problems 207

Suggest why these equations might be more practical for numerical integra-

tion than Eqs. (6.24a, b).

6.7 Take typical values of the poleward temperature flux due to transient

eddies in the northern hemisphere winter from Fig. 5.7(a). Hence, estimate

the Eliassen-Palm flux divergence in the upper troposphere and the rate

of change of zonal wind associated with the transient eddy temperature

flux. Compare this with the acceleration associated with the transient eddy

momentum flux convergence.

6.8 Starting from Eq. (5.37) which gives the rate of change of total eddy

energy, show that the rate of generation of eddy energy is related to the

Eliassen-Palm flux by:

Three-dimensional aspects of the global circulation

7.1 Zonal variations in the tropics

Up to this point, we have followed a traditional exposition of the global

circulation by concentrating upon the zonal mean circulation and upon the

zonal mean fields of eddy quantities. But the global circulation is far from

zonally symmetric. Tropical heating has distinct maxima at particular longit-

udes.

In the midlatitudes, the transient eddies are not distributed uniformly

around the latitude circles, but are concentrated into isolated 'storm tracks',

especially in the northern hemisphere. This chapter will be devoted to a

description of such zonal asymmetries and their consequences.

The various diagnostics of the steady and transient eddy activity which we

have considered in earlier chapters become small in the tropics. Eddy kinetic

energy is much smaller in the tropics than in the midlatitudes. Similarly,

eddy temperature and momentum

fluxes,

both steady and transient, are much

smaller in the tropics. Thus a picture emerges in which heat and momentum

are transported, essentially by axisymmetric motions in the tropics, with

eddies taking over in the subtropics and midlatitudes.

There is some truth in this picture. But it can also be misleading. First,

consider the heating fields shown in Fig. 3.8. The forcing of the circulation

is certainly not axisymmetric, especially in the tropics. Rather, there are

a small number of centres of intense heating. The most important is over

south-east Asia in the JJA season, and over Indonesia in the DJF season.

Other maxima are apparently associated with the continental land masses.

One matter that we will wish to consider is why such a highly localized

distribution of heating leads to a more or less axisymmetric response.

It must also be said that a closer look at the tropical zone shows that the

response is not entirely axisymmetric. Figures 7.1 and 7.2 show vectors of

the mean wind and near the tropopause and at low levels. The 15kPa level

208