Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

230
№ 1322
1)
⎥
⎦
⎤
⎢
⎣
⎡
π
+=
2
3
;0 2sinsin2 xxy
,
2
cos
2
3
cos222cos2cos2'
x
xxxy
⋅⋅=+= ,
()
3
2
3
0
2
3
cos
;0 при 0
2
3
cos
n
x
x
xx
π
+
π
==
π∈>
,
()
nx
x
x
x
π+π==
π∈>
2 0
2
cos
;0 при 0
2
cos
,
()
2
3
3
2
2
3
00 =
π
−=
π
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
yyy ,
(
)
0y
=
π
,
наиб.:
2
3
3
=
π
⎟
⎠
⎞
⎜
⎝
⎛
y ; наим.: 2
2
3
−=
π
⎟
⎠
⎞
⎜
⎝
⎛
y ;
2)
⎥
⎦
⎤
⎢
⎣
⎡
π
+=
2
;0 2cossin2 xxy
,
(
)
xxxxy sin21cos22sin2cos2'
−
=
−= ,
⎟
⎠
⎞
⎜
⎝
⎛
π
∈>
2
;0 при 0cos
xx ,
⎟
⎠
⎞
⎜
⎝
⎛
π
∈>−
6
;0 при 0sin21
xx , cледова-
тельно
у = 1,5 – точка максимума, у = 1 – точка минимума.
№ 1323
1)
[]
4;1 5 −+= xy , 0
52
1
' >
+
=
x
y
, следовательно,
у = 2 – минимум; у = 3 – максимум;
2)
⎥
⎦
⎤
⎢
⎣
⎡
π
+=
2
;0 cos22sin xxy
,
()
0cos3sin
3
22
cos
3
1
3sin22cos' =+α=−=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
xxxxxy ,
3
1
arccos=α
,
()
nxx π+
π
=+α=+α
2
0cos
,
⇒
2
,
2
;
22
0
π
−≤α≤π−π≤α−≤
ππ
≤π+
π
−α−≤ n
, что невозможно
⇒=
⎟
⎠
⎞
⎜
⎝
⎛
π
= 1
2
;22)0( yy наим.: у = 1; наиб.: 22=y .
№ 1324
1)
[
)
4;5,0 ln xxy −= ,
01
1
' =−=
x
y
,
()
44ln4 ;
2
1
2ln
2
1
;1 −=−−==
⎟
⎠
⎞
⎜
⎝
⎛
yyx
231
()
; 11 −=y наим. y(4) = ln4 – 4 наиб. y(1) = -1
2)
[]
1;0 1
2
xxy −= ,
2
1
,
2
1
;0
1
21
12
2
;1'
2
2
2
2
2
±===
−
−
=
−
⋅
−= xx
x
x
x
xx
xy ,
() ()
01 ; 00 == yy ,
2
1
2
1
2
1
2
1
=⋅=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
y , Наим. y = 0; Наиб.
2
1
y =
.
№ 1325
Обозначим радиус основания цилиндра через r, тогда объем цилиндра
()
322
233 rrrrV π−π=−π= ,
(
)
rrrrV −π=π⋅−π= 16236
2
.
Функция V(r) возрастает, при 0 < r < 1 и убывает при r < 0 и r > 1, сле-
довательно максимум функции Vбудет, при r = 1.
№ 1326
Площадь полной поверхности цилиндра
2
2254 rrhS π+π=π= , где r –
радиус основания, а h – высота, тогда объем
hrV
2
π= ,
2
2254 rrhS π+π=π= ,
,
27
2
r
r
h
−
=
тогда
(
)
(
)
32
22
27
27
rr
r
rr
V −π=
−π
= ,
(
)
(
)
,93327'
22
rrV −π=−π= тогда максимум V будет в точке r = 3, h = 6,
тогда максимальный объем V
max
= 54π
№ 1327
Обозначим за х сторону основания, а за h – высоту пирамиды, тогда по
условию х + h = 9;
()
,9
34
1
2
xxV −= и так как объем максимальный, то
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−= xxV
4
3
32
9
' , V’ = 0, тогда х = 6.
№ 1328
Обозначим за х сторону основания, а за h – высоту призмы, тогда
hxV ⋅=
2
, где х
2
выражается через h и длину диагонали по формуле:
2
12
2
2
h
x
−
=
, тогда
2
2
2
3
6' ,
2
12
hVh
h
V −=⋅
−
=
, откуда находим, что
максимум достигается при h = 2.
№ 1329
()
⎟
⎠
⎞
⎜
⎝
⎛
π
−π+=
−
2
;5,0 ;cos
2
Mxxxf
первообразная:
(
)
,sin
1
1
cxxxf ++−=
−
т.к.
232
π
−=
π
⎟
⎠
⎞
⎜
⎝
⎛
2
2
1
f запишем:
π
−=++
π
−
2
1
2
c
, откуда с = -1, следовательно
первообразная имеет вид:
1sin
1
1
−+−=
−
xxy .
№ 1330
() ( )
(
)
63 ,231232
2
≤≤−−−−= xxxxxf
(
)
(
)
;3666'243632'
223
−−=+−−= xxxxxxf
Функция возрастает при x < -2 и x > 3, и убывает при –2 < x < 3
() ()
(
)
(
)
1326 ,573 ,513 ,682
=
−
=
=
−=
−
ffff . Ответ: -57 и 132.
№ 1331
1)
()
(
)
2ln3ln
61
12
1
ln29
1
ln32'
22
+−=⋅+⋅⋅⋅−⋅⋅⋅= xx
xxx
x
x
xxf
()
;02ln3
2
ln
6
при 0' =+−=
⎟
⎠
⎞
⎜
⎝
⎛
xx
x
xf
,1ln и 2ln ,
2
893
ln ==
−±
= xxx
т.е. х = е
2
и х = е;
2)
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
∈∈
3
4
3
3
4
3
2
; ,; eeeeee ;
3)
()
(
)
()
5 ,4 ,
32
25
4 ,9
2
4
3
3
====
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
efefefef . Ответ: 4 и 9.
№ 1332
⎟
⎠
⎞
⎜
⎝
⎛
=
2
1
;2 ,
2
Axy ;
а)
()
(
)
;
2
21
2
21
2
yyxxd −+−= ,
2
1
;2
⎟
⎠
⎞
⎜
⎝
⎛
A следовательно
'
2
1
,2x
11
== y
(
)
,;
2
xxX следовательно ; ,
2
22
xyxx ==
()
0 ;
2
1
2
2
2
2
2
>−+−=
⎟
⎠
⎞
⎜
⎝
⎛
xxxd
б) рассмотрим
() ( )
2
2
1
2
2
⎟
⎠
⎞
⎜
⎝
⎛
−+−= xxxf и найдем ее наименьшнее
значение при x > 0.
()
;44'4
4
1
4'
4
1
44'
34422
xxxxxxxxf +−=+−=+−++−=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
()
0x'f = при - 1 ,1 ,044
33
=−=+− xxx стационарная точка

233
При переходе через единственную стационарную точку х = 1 производ-
ная меняет знак с «-» на «+», след. функция принимает в ней наименьшее
значение. Итак, расстояние будет наименьшим от А до точки (1;1).
№ 1333
AD – основание трапеции, поэтому BC(x) – отрезок, параллельный AD.
() ()()()
,1 причем ,
2
1
=⋅+= ADxhxBCADxS
() ()
(
)
т т.,211 ,2
22
xxxhxxBC −=−+==
() ()
()
(
)
10 где ,
2
1
21
242
2
1
221
2
1
32
322
≤<−−+=
=−−+=−+=
xxxx
xxxxxxS
Рассмотрим S'(x): S’(x) = 2 – x – 3x
2
; S’(x) = 0 при x = -1 или
3
2
x =
Из полученных критических точек только
3
2
x =
лежит в промежутке
(0;1]; при переходе через эту точку S’(x) меняет знак с «+» на «-», т.е. это
точка максимума.
Найдем значения S(x) на концах рассматриваемого промежутка и в по-
лученной критической точке.
()
121
2
1
0 =⋅⋅=S ,
27
49
3
2
=
⎟
⎠
⎞
⎜
⎝
⎛
S ,
()
,
2
3
1 =S таким образом
27
49
max
=S .
№ 1334
1)
[]
(
)
(
)
22
4; ;4; ;1;1 xxAxxBx −−∈ ;
2)
()
;6 ;
3
3 ,; xx
xx
yxC
c
c
cc
−=
+
=
2
2
2
412 ;
4
6 xy
yx
c
c
−=
+
= ;
3)
(
)
=−−⋅⋅=⋅=
22
44122
2
1
2
1
xxxCDABS
ABC
(
)
3
234 xx −
4) Рассмотрим функцию
(
)
(
)
3
234 xxxf −= на [0;1] и найдем ее наи-
большее значение.
()
(
)
,634'
2
xxf −=
()
()
-
2
1
;0634 при 0'
2
±==−⋅= xxxf стационарная точка.
При переходе через единственную стационарную точку
2
1
на [-1;1]
производная меняет знак с «+» на «-», следовательно в этой точке функция
принимает наибольшее значение.
5)
24
2
1
23
2
1
4
2
=⋅−⋅=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ABC
S
.
234
№ 1335
1
mi
n
,5 ;
2
==++= yxqpxxy
()
;
052
5251
;
05'
5251
⎩
⎨
⎧
⎩
⎨
⎧
=+⋅
++=
=
++=
p
qp
y
qp
откуда p = -10, q = 26.
№ 1336
Обозначим через r радиус основания, а через h – высоту конуса, тогда
объем
(
)
322
3
1
3
400
400
3
1
3
1
hhhhhrV π−π=−π=π=
,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−π=π−π=
3
20
3
20
3
400
'
2
hhhV , h > 0, след.
3
20
0
=h – точка
максимума (при переходе через h
0
V’ меняет знак с «+» на «-», таким обра-
зом
3
20
=h
.
№ 1337
Обозначим через r – радиус, через h – высоту цилиндра, тогда
22
22 a , rrhShrV π+π=⋅π=
,
2
2
2
2
2
222
; r
r
V
r
rVr
S
r
V
h π+=
π
π+⋅π
=
π
=
,
2
3
2
24
4
2
'
r
Vr
r
r
V
S
−π
=π+−=
, точка минимума ,
2
3
π
=
V
r
а минимальная
площадь
=π=
π
π+
π
=
⎟
⎠
⎞
⎜
⎝
⎛
3
2
3
3
2
3
2
3
3
min
22
2
2
22
VV
V
V
V
S
3
2
3
3
2
2323 VV π=π
.
№ 1338
Обозначим через r – радиус основания, через 2h – высоту цилиндра, то-
гда
rh4h2r2S π=⋅π= , где ,
22
rRh −= тогда
22
4 rRrS −π= .
(
)
(
)
=
−
π−−π
=
−
−π
+−π=
22
222
22
22
4422
4'
rR
rrR
rR
rr
rRS
(
)
22
22
22
22
2484
rR
rR
rR
rR
−
−π
=
−
π−π
=
,
2/
0
Rr =
– точка максимума, т.к. при
переходе через r
0
S’ меняет знак с «+» на «-», таким образом
2
R
r =
.
№ 1339
Обозначим через r – радиус основания, через 2h – высоту цилиндра, то-
гда
2222
rRrhrV −π=π=
235
()()()
22
32
22
322
22
3
22222
322
2''
rR
rrR
rR
rrRr
rR
r
rRrrRrV
−
−π
=
−
−−π
=
=
−
−−π=−π=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Rr
3
2
0
= – точка максимума, т.к. при переходе через r
0
V’ меняет знак
с «+» на «-», тогда
3
3
2
22
R
RRh =−=
, соответственно высота
3
2
2
R
h =
№ 1340
Обозначим через h высоту конуса, тогда радиус основания
()
2
3
RhRr −−= , а
()
()
(
)
(
)
2222
2
2
2
3
1
2
3
1
3
1
hhRhhRhRhRhRhRV −π=−+−π=−−π=
()
()
()
;3
3
1
222
3
1
'
2
hRhhRhhhRV −π=−+−π=
Rh
3
4
0
= – точка максимума.
№ 1341
α⋅⋅=
⋅=⋅=
⋅π=⋅=
sin
2
1
3
1
3
1
задана -
3
1
3
1
2
BCABS
hShSS
hRhSS
ABC
ABCоснпир
оснкон
22
sin2
α
−
π
=∠=∠α= BCABACRAC
2
cos2
sin
2
cossin2
sin
22
sin
α
=
α
α
⋅α
=
α
=
α
−
π
⎟
⎠
⎞
⎜
⎝
⎛
R
R
AB
ACAB
α
α
=α⋅
α
⋅= sin
2
2
cos исследуем sin
2
2
cos
2
4
2
1
fR
ABC
S
(
)
2
1
cos
2
1
cossincoscos
2
1
'
2
cos1
sin'
222
−α+α=α−α+α=
α+
⋅α=
⎟
⎠
⎞
⎜
⎝
⎛
f
981 01cos
2
cos2 0' =+==−α+α= Df ;
2
1
cos;1cos
21
=α−=α , следовательно сумма всех углов треугольника
3
,,2
3
;
2
π
=α⇒∈π+
π
±=απ
Znn
.
A C
D
α
236
№ 1342
Обозначим через r – радиус основания, тогда высота
22
2
−=
p
h
, а
объем
⎟
⎠
⎞
⎜
⎝
⎛
−
π=π=
2
4
22
rp
rhrV
,
(
)
()
;62
2
122
2
'
2
rprrrpV −⋅
π
=−
π
=
-
6
0
p
r =
точка максимума, тогда
2163236
max
32
pppp
V
π
=−
π
=
⎟
⎠
⎞
⎜
⎝
⎛
.
№ 1343
Пусть АО
1
= х, тогда ;
22
1
rROO −=
0 ;2 ;2
642222
>−π=−⋅⋅π= xxxRVrRxV и Rx
<
Рассмотрим функцию
()
642
2 xxRxg −π= при 0 < x < R и найдем ее
наибольшее значение, заметим, что g(x) принимает наибольшее значение в
той же точке, что и
()
642
xxRxf −=
.
(
)
;64'
532
xxRxf −=
3
2
2
0
R
x =
– точка максимума, тогда
3
2
RH = .
№ 1344
Пусть r – радиус основания, H – высота цилиндра, тогда
2
4
2
2
242
r
rVr
rrHS
π+
=π+π=
, где V – объем
(
)
3
0
2
3
4
;
42
'
π
=
−π
=
V
r
r
Vr
S
- точка минимума, следовательно расход
жести будет наименьшим, когда
2
1
4
2
44
2
2
2
33
=
π⋅
⋅π
=
π
⋅π⋅
π
⋅
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
V
V
V
VV
H
r
,
т.е. при 2D = H. (Опечатка в ответе задачника).
№ 1345
Пусть ОО
1
= х, тогда ;
22
1
rRAO −= О
2
О
1
= 2х;
(
)
;
4
33
22
0
rRS −=
()
(
)
3222
2
33
2
4
33
xxRxrR
пр
V −=−=
, причем x > 0 и x < R.
Рассмотрим
()
(
)
32
2
33
xxRxf −=
на (0;R) и найдем ее наибольшее
значение:
()
(
)
22
3
2
33
' xRxf −= ,
3
R
x =
– точка максимума, тогда наи-
больший объем призма имеет при высоте
3
2R
.
237
№ 1346
Пусть АО = x, тогда из подобия треугольников MOS и BO
1
S получим
(
)
; ; ;
R
xRH
h
H
hH
R
x
H
b
R
x
−
=
−
==
()
(
)
322
xRx
R
H
R
xRH
xV −
π
=
−⋅
⋅⋅π= , причем x > 0 и x < R.
Рассмотрим функцию
()
(
)
32
xRx
R
H
xf −
π
=
на (0;R) и найдем ее наи-
большее значение.
()
()
2
32 xRx
R
πH
xf' −=
,
3
2R
x =
– точка максимума, таким образом
наибольший объем у цилиндра будет при
3
3
,
3
2 H
R
RH
h
R
r =
⋅
==
.
№ 1347
1)
()
493
23
+−+= xxxxf
()
(
)
(
)
(
)
313323963
22
+−=−+=−+= xxxxxxxf'
х = -3 – точка максимума;
х = 1 – точка минимума.
+
–
+
-3 1
2)
()
52
54
+−= xxxf ,
() ( )
⎟
⎠
⎞
⎜
⎝
⎛
−=−=−= xxxxxxxf'
10
4
104104
3343
;
+
–
–
0 0,4
х = 0 – точка минимума
х = 0,4 – точка максимума
№ 1348
1) D(y) = IR, непрерывная, непериодиче-
ская, т.к. задана многочленом
2) y(-x) = -x
3
+ 3x + 2 – ни четная, ни не-
четная
3) y = 0 при x
3
– 3x + 2 = 0; x = 1; x = -2
4) y’ = 3x
2
– 3; y = 0 при 3x
2
– 3 = 0;
3(x – 1)(x + 1) = 0; x = ± 1 – стационарные
точки
5) (-
∞
;-1) – функция возрастает
(-1;1) – функция убывает
(1;+
∞
) – функция возрастает
6) k = tgα, α = 0 при k = 0; f’(x) = 0, т.е.
х = -1, х = 1, т.е. (1;0), (-1;4).
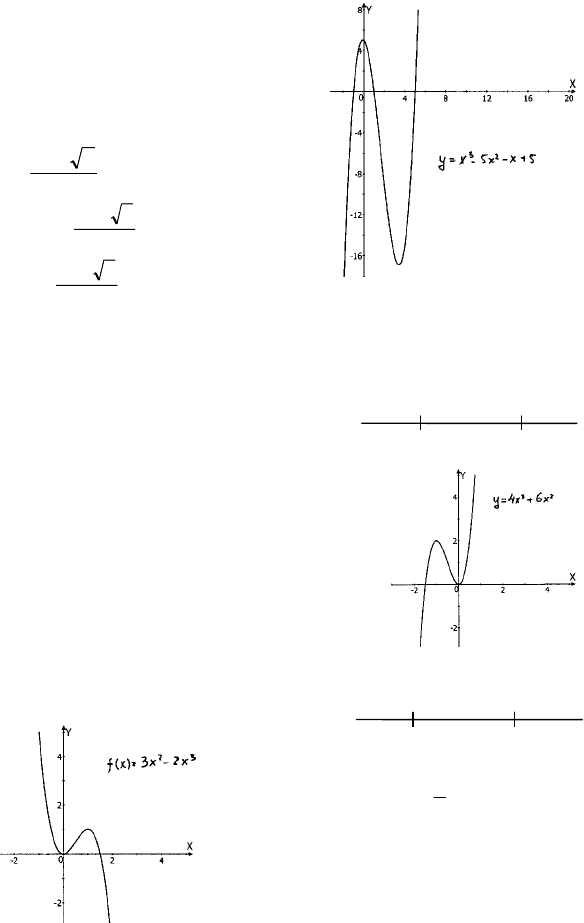
238
№ 1349
1. D(y) = R
2. y(-x) = -x
3
- 5x
2
+ x + 5 – ни четная,
ни нечетная
3. y = 0 при х
3
– 5х
2
– х + 5 = 0; х = 1,
х = 5, х = -1
4. y′ = 3x
2
– 10x – 1
y’ = 0 при 3x
2
– 10x – 1 = 0;
3
725
x
±
=
5.
3
725
x
−
= — точка максимума
3
725
x
+
= — точка минимума
6. y = f(x
0
) + f’(x
0
)(x – x
0
); x
0
= 4
f(4) = -15, f
′
(4) = 3x
2
– 10x –1, f
′
(4) = 7, y = 7x – 43
№ 1350
1) f(x) = 4x
3
+ 6x
2
а) D(y) = R
б) f(-x)=-4x
3
+6x
2
– ни четная, ни нечетная
в) f(x) = 0 при 4x
3
+ 6x
2
= 0; x
2
(4x+6)=0, x = 0,
x = -1,5
г) f’(x) = 12x
2
+ 12x = 12x(x + 1)
х = -1 – точка максимума
х = 0 – точка минимума
2) f(x) = 3x
2
– 2x
3
; а) D(y) = R
б) f(-x) = 3x
2
+ 2x
3
– функция ни четная, ни нечетная
в) f(x) = 0 при 3x
2
– 2x
3
= 0,
x
2
(3 – 2x) = 0, x = 0,
2
3
x
=
г) f’(x) = 6x – 6x
2
= 6x(1 – x)
x = 0 – точка минимума
х = 1 – точка максимума
+ +
–
-1 0
+
–
–
0 1
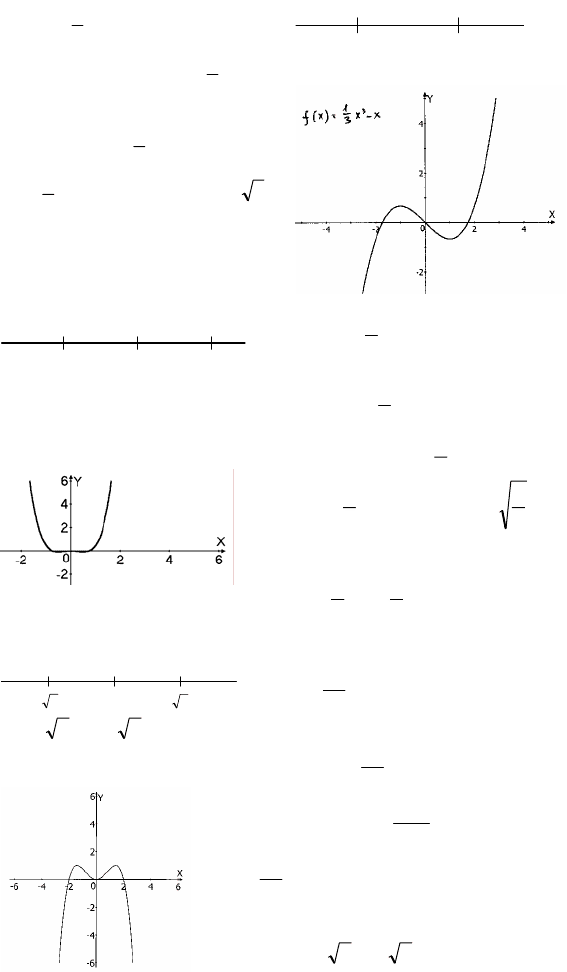
239
3)
()
xx
3
1
xf
3
−=
;
а) D(y) = R; б)
()
xx
3
1
xf
3
+−=−
,
следовательно функция нечетная
в)
()
3,0 ,01
3
1
;0
3
1
при 0
2
3
±===
⎟
⎠
⎞
⎜
⎝
⎛
−
=−=
xxxx
xxxf
;
x = -1 – точка максимума
х = 1 – точка минимума
+ +
–
-1 1
–
+
–
+
-½ 0 ½
х = -½, x = ½ – точки мини-
мума
х = 0 – точка максимума
4)
()
24
x
2
1
xxf −=
а) D(y) = R
б)
()
24
x
2
1
xxf −=−
- функция четная
в)
()
2
1
,0 ,0
2
1
,0
2
1
при 0
22
24
±===
⎟
⎠
⎞
⎜
⎝
⎛
−
=−=
xxxx
xxxf
г)
(
)
(
)
=−=−= 144'
23
xxxxxf
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−=
2
1
2
1
4 xxx
№ 1351
+
+
– –
2−
0
2
2 ,2 =−= xx – точки
максимума
х = 0 – точка минимума
1)
2
4
4
x
x
y +−=
а) D(y) = IR
б)
()
2
4
4
x
x
xf +−=−
– функция четная
в)
()
;0
4
при 0
2
4
=+
−
= x
x
xf
(
)
04
4
2
2
=+− x
x
; x = 0, x = ±2
г)
(
)
(
)
=+−=+−= 22'
23
xxxxxf
(
)
(
)
22 +−−= xxx
