Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

200
2) log
8
(x
2
– 4x + 3) ≤ 1
⎪
⎩
⎪
⎨
⎧
≤+−
>+−
834
034
2
2
xx
xx
()
(
)
()()
⎩
⎨
⎧
≤−+
>−−
051
031
xx
xx
(
)
(
)
[]
⎩
⎨
⎧
−∈
+∞∞−∈
5;1
;31;
x
x
U
[
)(
]
5;31;1 U−∈x .
№ 1227
1) 0
1
13
loglog
2
1
2
1
≤
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
x
x
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≥
−
+
>
−
+
>
−
+
0
1
13
log
0
1
13
log
0
1
13
2
1
2
1
x
x
x
x
x
x
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≤
−
+
<
−
+
>
−
+
2
1
1
13
1
1
13
0
1
3
1
x
x
x
x
x
x
()
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≤
−
+−+
<
−
+−+
+∞−∞−∈
0
1
126
0
1
113
;1
3
1
;
x
xx
x
xx
x
U
()
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
≤
−
+
<
−
+
+∞
⎟
⎠
⎞
⎜
⎝
⎛
−∞−∈
0
1
5
3
0
1
1
;1
3
1
;
x
x
x
x
x U
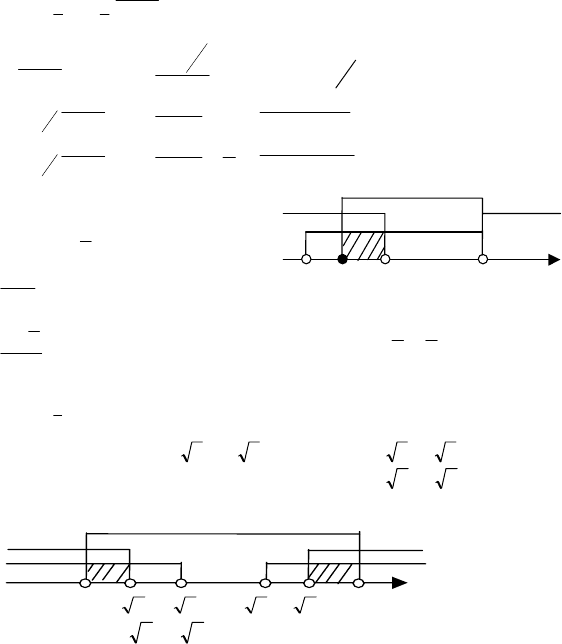
–
1
1
–
3/5
–
1/3
Ответ:
⎟
⎠
⎞
⎢
⎣
⎡
−−∈
3
1
;
5
3
x
2)
(
)
(
)
05loglog
2
4
3
1
>−x
()
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>−
>−
>−
15log
05log
05
2
4
2
4
2
x
x
x
()
(
)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<−
>−
>+−
45
15
055
2
2
x
x
xx
(
)
(
)
()()
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−∈
+∞−∞−∈
+∞−∞−∈
3;3
;66;
;55;
x
x
x
U
U
–
3
6−
3
5− 5 6
Ответ: x
(
)
(
)
3;66;3 U−−∈ .
№ 1228
1) (x
2
– 4)log
0,5
x > 0, x > 0 по определению логарифма
а)
()()
⎩
⎨
⎧
>
>+−
0log
022
5,0
x
xx
; б)
(
)
(
)
⎩
⎨
⎧
<
<+−
0log
022
5,0
x
xx
;
201
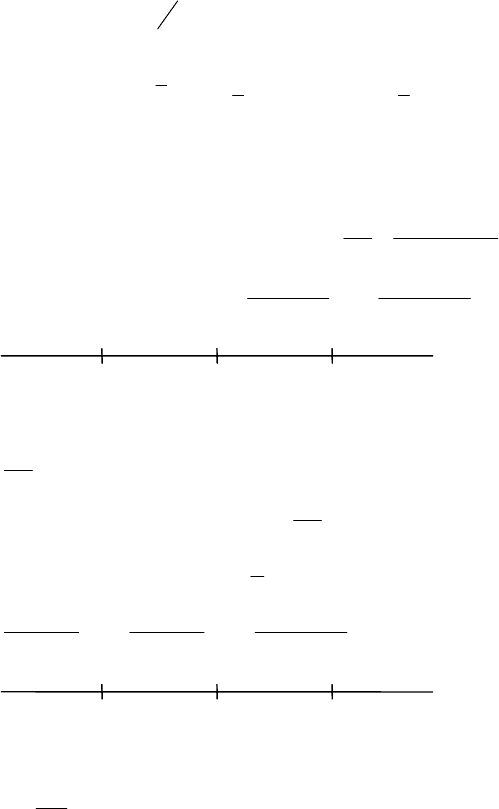
а)
()()
⎩
⎨
⎧
<
+∞−∞−∈
1
;22;
x
x
U
x ∈ (-∞;-2); б)
(
)
⎩
⎨
⎧
>
−∈
1
2;2
x
x
x ∈ (1; 2)
Т.к. х > 0, то х ∈ (1, 2). Ответ:
(
)
2;1∈x
2) (3х – 1)log
2
x < 0
а)
⎩
⎨
⎧
>
>−
0log
013
2
x
x
⎪
⎩
⎪
⎨
⎧
>
>
1
3
1
x
x
⇒ x > 1
б)
⎩
⎨
⎧
<
<−
0log
013
2
x
x
⎪
⎩
⎪
⎨
⎧
<
<
1
3
1
x
x
⇒
3
1
<
x . Ответ:
()
+∞
⎟
⎠
⎞
⎜
⎝
⎛
∈ ;1
3
1
;0 Ux
№ 1129
1) x
1+lgx
< 0,1
-2
, x > 0; x
1+lgx
< 10
2
.
Ясно, что х = 1 решение нашего неравенства
а) x > 0, x < 1, log
x
x
1+lgx
> log
x
10
2
,
x
x
lg
2
lg1 >+ ,
0
lg
2lglg
2
>
−+
x
xx
Сделаем замену: lgx = a, а ≠ 0,
(
)
0
2
2
>
−+
a
aa
,
(
)
(
)
0
21
>
+−
a
aa
–
–
+
+
-2 0 1
()()
+∞−∈ ;10;2 Ua , т.е. -2 < lgx < 0 и lgx > 1,
0,01 < x < 1 и x > 10, но т.к. x > 0 и x < 1, то решением является
1
100
1
<< x
б) x > 1, log
x
x
1+lgx
< 2log
x
10, 0
lg
2
lg1 <−+
x
x .
Сделаем замену: lgx = a,
0
2
1 <−+
a
a , a ≠ 0
0
2
2
<
−+
a
aa
, 0
2
2
<
−+
a
aa
,
(
)
(
)
0
21
<
+−
a
aa
–
–
+
+
-2 0 1
()()
1;02; U−∞−∈a , т.е.
lgx < -2 и 0 < lgx < 1
100
1
<x и 1 < x < 10 т.е. x > 1, то решением является 1 < x < 10
Ответ:
()
(
)
[
]
110;11;001,0 UU∈x .
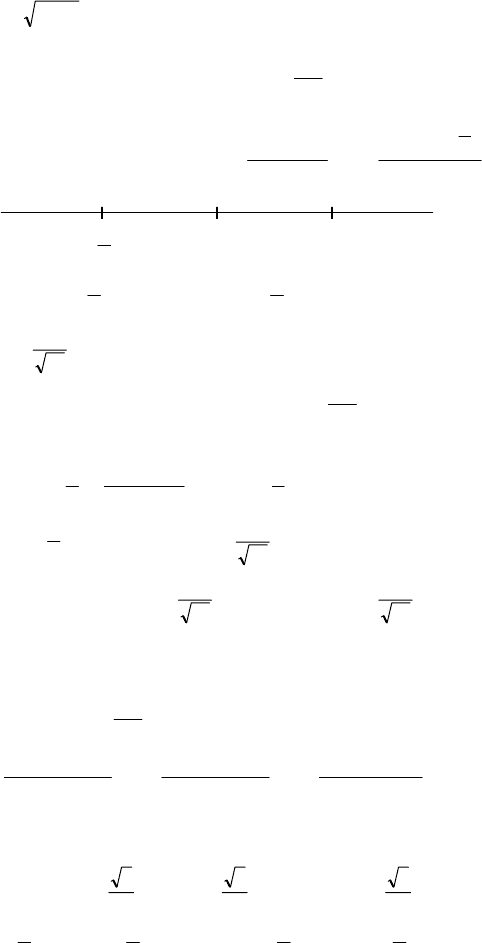
202
2)
xx
x
10
lg4
<
.
Ясно, что x = 1 – решение нашего неравенства
а) x > 1, log
x
x
2lgx
< log
x
10x,
x
x
lg
1
1lg2 +< .
Сделаем замену: lgx = a, а ≠ 0,
0
12
2
<
−−
a
aa
,
()
0
2
1
1
<
⎟
⎠
⎞
⎜
⎝
⎛
+−
a
aa
–
–
+
+
-
2
1
0 1
()
1;0
2
1
; U
⎟
⎠
⎞
⎜
⎝
⎛
−∞−∈a , т.е.
2
1
lg
−<x и 0 < lgx < 1
10
1
<x и 1 < x < 10 т.к. x > 1, то решением является 1 < x < 10;
б) 0 < x < 1, log
x
x
2lgx
> log
x
10x,
x
x
lg
1
1lg2 +> .
Сделаем замену: lgx = a, а ≠ 0
a
a
1
12 +>
, 0
12
2
>
−−
a
aa
,
()
+∞
⎟
⎠
⎞
⎜
⎝
⎛
∈ ;10;
2
1
Ua
,
т.е.
0lg
2
1
<<−
x и lgx > 1, 1
10
1
<< x и x > 10; т.к. 0 < x < 1,
то решением является
1
10
1
<< x . Ответ:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∈ 10;
10
1
x .
3) x + 3 > log
3
(26 + 3
x
), 26 + 3
x
> 0 при любых х, log
3
3
x+3
> log
3
(26 + 3
x
),
3
x+3
> 26 + 3
x
, 3
x+3
– 26 – 3
x
> 0, 26 ⋅ 3
x
– 26 > 0, 3
x
> 1, x > 0;
4) 3 – x < log
5
(20 + 5
x
), 20 + 5
x
> 0 при любых х, log
5
5
3-x
< log
5
(20 + 5
x
),
5
3-x
< 20 + 5
x
, 0520
5
125
<−−
x
x
, 5
x
= a > 0
0
20125
2
<
−−
a
aa
, 0
12520
2
>
−+
a
aa
,
(
)
(
)
0
525
>
+−
a
aa
,
()( )
+∞−∈ ;250;5 Ua , т.е. -5 < 5
x
< 0 и 5
x
> 25, x =
φ
и x>2, т.е. x > 2;
№ 1230
1)
()
2
3
3cos ≥− x ,
()
2
3
3cos ≥x , 3x = y,
2
3
cos ≥y ,
Znnyn ∈π+
π
≤≤π+
π
− ,2
6
2
6
, Znnxn ∈π+
π
≤≤π+
π
− ,2
6
32
6
,
203
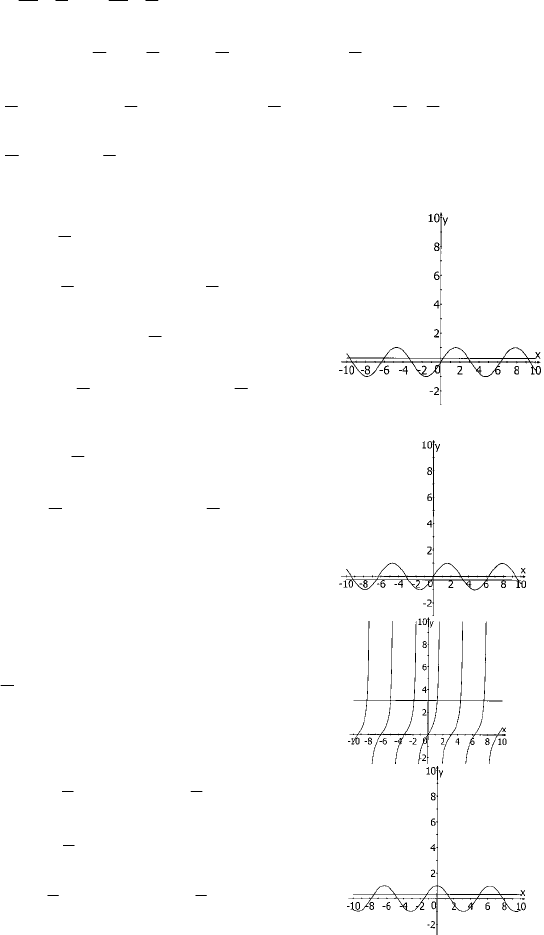
Znnn ∈π+
π
≤π+
π
− ,
3
2
183
2
18
;
2)
2
1
3
2cos −<
⎟
⎠
⎞
⎜
⎝
⎛
π
−x ,
yx =
π
−
3
2
,
2
1
cos −<y
;
Znnyn ∈π+π<<π+π ,2
3
4
2
3
2
,
Znnxn ∈π+π<
π
−<π+π ,2
3
4
3
22
3
2
Znnxn ∈π+π<<π+
π
,
6
5
2
№ 1231
1)
4
1
sin <x
4
1
arcsin=b
,
4
1
arcsin−π−=a
4
1
arcsin2 −π=+π= ac
Zn
nxn
∈
π+<<π+−π−
,2
4
1
arcsin2
4
1
arcsin
2)
4
1
sin −>x
Znn
xn
∈π+π+
+<<π+−
,2
4
1
arcsin2
4
1
arcsin
3) tgx – 3 ≤ 0
tgx ≤ 3
Znnarctgxn ∈π+≤<π+
π
− ,3
2
4)
3
1
cos >x ;
⎟
⎠
⎞
⎜
⎝
⎛
−=
3
1
arccosa
3
1
arccos=b
Znnxn ∈π+<<π+− ,2
3
1
arccos2
3
1
arccos
204
№ 1232
1) 03cos2 <−x [-3π; π]
2
3
cos <x
π
−
=π−=
π−=π−=
π
=
π
=
6
13
2
,
6
11
2 ,
6
-
b ,
6
bd
aca
⎥
⎦
⎤
⎜
⎝
⎛
π
π
⎟
⎠
⎞
⎜
⎝
⎛
π
−π−
⎟
⎠
⎞
⎢
⎣
⎡
π−π−∈ ;
66
;
6
11
6
13
;3 UUx
2)
01sin2 ≥+x [-3π; π]
2
1
sin −≥
x
⎥
⎦
⎤
⎢
⎣
⎡
π
π
−
⎥
⎦
⎤
⎢
⎣
⎡
π−
π
−
⎥
⎦
⎤
⎢
⎣
⎡
π−π−∈ ;
44
3
;
4
9
4
11
;3 UU
x
3)
03 ≤+ tgx , [-3π; π]
3−≤tgx ,
3
π
−=a
,
π=
π
−π=
3
2
3
b
,
π−=π−
π−
=
3
4
3
c
,
π−=π−π−=π−=
3
7
3
4
cd
,
⎟
⎠
⎞
⎢
⎣
⎡
ππ
⎥
⎦
⎤
⎜
⎝
⎛
π
−
π
−
⎥
⎦
⎤
⎜
⎝
⎛
π−π−
⎥
⎦
⎤
⎜
⎝
⎛
π−π−∈
3
;
23
;
2
3
4
;
2
3
3
7
;
2
5
UU
UUx
4) 3tgx – 2 > 0, [-3π; π]
3
2
>tgx
3
2
arctga =
UU
⎟
⎠
⎞
⎜
⎝
⎛
π
−π−
⎟
⎠
⎞
⎜
⎝
⎛
π−
π−∈
2
3
;2
3
2
2
5
;3
3
2
arctgarctgx
⎟
⎠
⎞
⎜
⎝
⎛
π
⎟
⎠
⎞
⎜
⎝
⎛
π
−π−
2
;
3
2
2
;
3
2
arctgarctg UU

205
№ 1233
1) Рассмотрим очевидное неравенство (a – b)
2
≥ 0; преобразуем его:
a
2
– 2ab + b
2
≥ 0, a
2
+ b
2
≥ 2ab,
ab
ba
≥
+
2
22
, что и требовалось доказать
2) Преобразуем неравенство:
8
33
2
322333
babbaaba +++
>
+
;
0
8
3344
322333
>
−−−−+ babbaaba
; 0
8
3333
2233
>
−−+ abbaba
;
(
)
()
0
8
33
33
>
+−+ baabba
;
(
)
(
)
0
18
3
33
>
+−+
⋅
baabba
;
a
3
+ b
3
– ab(a + b) = (a + b)(a
2
– 2ab + b
2
) = (a + b)(a – b)
2
, при a, b > 0 и
a ≠ b (a + b)(a – b)
2
> 0, следовательно, исходное неравенство верно.
№ 1234
1) (a+b)(ab+1)≥4ab. Пусть ab=x, тогда
b
x
a =
и неравенство примет вид:
b
b
x
b
b
x
b
b
x
⋅≥
⎟
⎠
⎞
⎜
⎝
⎛
+⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
4
1
;
(
)
(
)
0
41
2
≥
−++
b
bxxbx
; 0
4
222
≥
−+++
b
bxbxxbx
;
(
)
(
)
0
212
222
≥
+−++−
b
bbxbbxx
;
(
)
(
)
0
1
22
≥
−+−
b
bxbx
.
Сделаем обратную подстановку:
(
)
(
)
0
1
22
≥
−+−
b
babbab
.
Неравенство верно, т.к. (ab – b)
2
> 0, ab > 0, b > 0, (1 – b)
2
≥ 0;
2) a
4
+ 6a
2
b
2
+ b
2
> 4ab(a
2
+ b
2
), (a
4
+ 2a
2
b + b
4
) + 4a
2
b
2
> 4ab(a
2
+ b
2
),
(a
2
+b
2
)
2
+4a
2
b
2
>4ab(a
2
+b
2
), (a
2
+b
2
)
2
–4ab(a
2
+b
2
)+4a
2
b
2
>0, но ((a
2
+b
2
)–2ab)
2
> 0
при всех a, b таких, что a
2
+ b
2
– 2ab ≠ 0, т.е. при (a – b)
2
≠ 0, a ≠ b.
№ 1235
1)
3≥++
a
c
c
b
b
a
,
1
3
1
≥
⎟
⎠
⎞
⎜
⎝
⎛
++
a
c
c
b
b
a
Слева стоит среднее арифметическое чисел
c
b
b
a
,
и
a
c
, а справа их
среднее геометрическое. Т.к. среднее геометрическое всегда не превышает
среднего арифметического, то неравенство верно для любых a>0, b>0, c>0
2) 2a
2
+b
2
+c
2
≥2a(b+c), a
2
+a
2
+b
2
+c
2
–2ab–2ac≥0, (a–b)
2
+(a–c)
2
≥ 0 – верно.
№ 1236
1)
⎩
⎨
⎧
=+
=−
1756
375
yx
yx
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+
+
+
=
175
5
736
5
73
y
y
y
x
206
18 + 42у + 25у = 85, 67у = 67, у = 1,
2
5
73
=
+
=
y
x
. Ответ: (2; 1).
2)
⎩
⎨
⎧
=++
=−−
012
0132
yx
yx
⎩
⎨
⎧
=−−−−
−−=
013)12(2
12
yy
yx
-4у – 2 – у – 13 = 0, -5у = 15, у = -3, х = 5. Ответ: (5; -3).
№ 1237
1)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+
=
+
−
−
10
25
10
25
yx
yxyx
⎩
⎨
⎧
=+
=−−−
10052
1005522
yx
yxyx
⎪
⎩
⎪
⎨
⎧
−
=
=−−
2
5100
10073
y
x
yx
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−
=
=−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
2
5100
1007
2
5100
3
y
x
y
y
-300 + 15у – 14у = 200, у = 500, х = -1200. Ответ: (-1200; 500).
2)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
−
−
+
=
−
+
+
0
34
6
32
yxyx
yxyx
⎩
⎨
⎧
=+−+
=−−++
04433
0362233
yxyx
yxyx
⎩
⎨
⎧
=−
=−+
07
0365
xy
yx
⎩
⎨
⎧
=
=−+
yx
yy
7
03635
у = 1, х = 7. Ответ
: (7; 1).
№ 1238
1)
⎪
⎩
⎪
⎨
⎧
=+
=+
25
5
22
2
yx
xy
()
⎪
⎩
⎪
⎨
⎧
=−+
−=
255
5
2
22
2
xx
xy
х
2
+ х
4
– 10х
2
+ 25 = 25, х
4
– 9х
2
= 0, х
2
(х
2
– 9) = 0, х
2
(х – 3)(х + 3) = 0,
х = 0, х = ±3, у = -5, у = 4.
Ответ: (0, -5), (3, 4), (-3, 4).
2)
⎪
⎩
⎪
⎨
⎧
=
=
4
16
y
x
xy
;
⎩
⎨
⎧
=
=
yx
xy
4
16
;
⎩
⎨
⎧
=
=
yx
y
4
164
2
, у = ±2, х = ±8. Ответ: (±8, ±2).
3)
⎩
⎨
⎧
=
=+
yx
yx
2
962
22
⎩
⎨
⎧
=
=+
yx
yy
2
9624
22
⎩
⎨
⎧
=
=
yx
y
2
16
2
, у = ±4, х = ±8.
Ответ: (±8, ±4)
№ 1239
1)
⎩
⎨
⎧
=−
=−
1
13
22
yx
yx
()
⎩
⎨
⎧
+=
=−+
1
131
2
2
yx
yy
⎩
⎨
⎧
+=
=−++
1
1321
22
yx
yyy
, у = 6, х = 7.
Ответ: (7, 6).

207
2)
⎩
⎨
⎧
=+
−=−
2337
53
2
yx
yx
⎪
⎩
⎪
⎨
⎧
−
=
−=−
3
723
53
2
x
y
yx
, х
2
– 23 + 7х + 5 = 0, х
2
+ 7х – 18 = 0,
х
1
= 2, х
2
= -9, у
1
= 3, у
2
=
3
2
28 . Ответ: (2, 3), (-9,
3
2
28 ).
№ 1240
1)
⎪
⎩
⎪
⎨
⎧
=+
=−
20
2
3
22
yx
x
y
y
x
. Пусть t
y
x
=
, тогда
2
31
=−
t
t
;
2
31
2
=
−
t
t
; 2t
2
–3t–2 = 0,
t
1
= 2, t
2
=
2
1
−
, отсюда а) 2=
y
x
и б)
2
1
−=
y
x
;
а) х = 2у и (2у)
2
+ у
2
= 20, 5у
2
= 20,
24 ±=±=y
, х = ±4;
б)
yx
2
1
−=
и 20
2
1
2
2
=+
⎟
⎠
⎞
⎜
⎝
⎛
− yy , у = ±4, х = ±2.
Ответ: (±4, ±2), (±2, ±4).
2)
⎪
⎩
⎪
⎨
⎧
=−
=+
8
3
1
3
22
yx
y
x
x
y
⎪
⎩
⎪
⎨
⎧
=−
=+
8
3
10
22
yx
y
x
x
y
.
Обозначим:
t
x
y
=
, тогда
3
101
=+
t
t
, 3t
2
+ 3 – 10t = 0, 3t
2
– 10t + 3 = 0,
t
1
= 3, t
2
=
3
1
;
а)
3=
x
y
, у = 3х, х
2
– 9х
2
= 8, -8х
2
= 8, х
2
= -1, решений нет
б)
3
1
=
x
y
; х = 3у, 9у
2
– у
2
= 8, у = ±1, х = ±3. Ответ: (±3, ±1).
3)
⎪
⎩
⎪
⎨
⎧
+=
+=
yxy
yxx
134
413
2
2
, вычтем уравнения: х
2
– у
2
= 9(х – у),
(х – у)(х + у) – 9(х – у) = 0, (х–у)(х+у–9) = 0 – либо х = у, либо х = 9 – у
а) х=у, х
2
=13х+4х, х
2
–17х=0, х(х–17)=0, х
1
=0, х
2
=17, у
1
=0, у
2
=17;
б) х=9–у, у
2
=4(9–у)+13у, у
2
–9у–36=0, у
1
=-3, у
2
=12, х
1
= 12, х
2
= -3.
Ответ: (0, 0), (17, 17), (12, -3), (-3, 12).
4)
⎪
⎩
⎪
⎨
⎧
=++
=−+
5232
4043
22
22
xyx
xyx
, вычтем уравнения: х
2
– 7х = -12,
х
2
–7х+12=0, х
2
–7х+12=0,
2
17
2
48497
2
1
±
=
−±
=x , х
1
= 4, х
2
= 3;
208
а) х = 4, 32 + у
2
+ 12 = 52, у
2
= 8,
22±=y
;
б) х = 3, 18 + у
2
+ 9 = 52, у
2
= 25, у = ±5. Ответ: (4, 22± ), (3, ±5).
№ 1241
1)
⎪
⎩
⎪
⎨
⎧
=
=
−
+
273
322
3 xy
yx
;
⎪
⎩
⎪
⎨
⎧
=
=
−
+
33
5
33
22
xy
yx
;
⎩
⎨
⎧
=−
=+
33
5
xy
yx
;
⎩
⎨
⎧
=+−
−=
353
5
yy
yx
4у = 8, у = 2, тогда х = 3. Ответ: (3, 2).
2)
⎪
⎩
⎪
⎨
⎧
=−
=−
723
7723
2
2
y
x
yx
. Пусть ba
y
x
== 2 ,3
2
; a, b>0, тогда система примет вид:
⎩
⎨
⎧
=−
=−
7
77
22
ba
ba
⎩
⎨
⎧
+=
=−
7
77
22
ba
ba
()
⎩
⎨
⎧
+=
=−+
7
777
2
2
ba
bb
⎩
⎨
⎧
+=
=−+
7
2814
22
ba
bbb
⎩
⎨
⎧
=
=
9
2
a
b
, тогда
2
2
33 =
x
, х = 4, 2
у
= 2, у = 1. Ответ: (4, 1)
3)
()
⎪
⎩
⎪
⎨
⎧
=−
=⋅
4log
57623
2
xy
yx
()
⎪
⎩
⎪
⎨
⎧
=−
⋅=⋅
4
22
62
2loglog
2323
xy
yx
⎩
⎨
⎧
=−
⋅=⋅
4
2323
62
xy
yx
⎩
⎨
⎧
+=
⋅=⋅
4
2323
62
xy
yx
3
х
⋅ 2
х+4
= 3
2
⋅ 2
6
, 3
х
⋅ 2
х
= 3
2
⋅ 2
2
Т.к. функция 3
х
⋅ 2
х
возрастает, то решение единственное. Отсюда
х = 2, у = 6. Ответ: (2, 6)
4)
⎩
⎨
⎧
=
=+
1000
4lglg
lg y
x
yx
⎪
⎩
⎪
⎨
⎧
=
=
1000
10lglg
lg
4
y
x
xy
⎪
⎩
⎪
⎨
⎧
=
=
1000loglog
10
lg
4
x
y
x
x
xy
⎪
⎩
⎪
⎨
⎧
=
=
3
4
10loglg
10
x
y
xy
⎪
⎩
⎪
⎨
⎧
=
=
10log3lg
10
4
x
y
x
y
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=
xx
x
y
10
4
4
log
310
lg
10
xx lg
310
lg
4
=
x
x
lg
3
lg4 =−
Пусть lgx = a, 4a – a
2
– 3 = 0, a
2
– 4a + 3 = 0, a
1
= 1, a
2
= 3;
1) a = 1, lgx = 1, x = 10, у = 10
3
; 2) a = 3, lgx = 3, х = 10
3
, у = 10.
Ответ: (10, 1000), (1000, 10).
№ 1242
1)
⎩
⎨
⎧
=+−
=−
045
0loglog
22
24
yx
yx
⎪
⎩
⎪
⎨
⎧
=+−
=−
045
0loglog
2
1
22
22
yx
yx
⎪
⎩
⎪
⎨
⎧
=+−
=
045
0log
22
2
yx
yx
209
⎪
⎩
⎪
⎨
⎧
=+−
=
045
1
22
yx
yx
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+−
=
04
5
1
2
x
x
x
y
х
3
+ 4х – 5 = 0,
1 x 0 5)x(x 1)-(x5 -x 4x
23
=⇔=++=+ (т.к. х
2
+ х + 5 > 0 при любом
х ∈ R), х = 1 – единственный действительный корень; у = 1. Ответ: (1, 1).
2)
⎩
⎨
⎧
=+
=+
3log2log
16
22
42
yx
yx
⎪
⎩
⎪
⎨
⎧
=
=+
32
42
2
16
xy
yx
⎪
⎩
⎪
⎨
⎧
=
=+
x
y
yx
8
16
2
42
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=+
x
y
x
x
8
16
8
2
2
2
2
⎪
⎩
⎪
⎨
⎧
=
=+−
x
y
xx
8
06416
2
24
(
)
⎪
⎩
⎪
⎨
⎧
=
=−
x
y
x
8
08
2
2
2
⎪
⎩
⎪
⎨
⎧
=
±=
8
8
y
x
, но х, у > 0 по определению логарифма. Ответ:
(
)
4
8,8.
№ 1243
1)
⎪
⎩
⎪
⎨
⎧
=−
=+
2
16
yx
yx
.
Пусть
0,0, , ≥≥== habyax , тогда система примет вид:
⎩
⎨
⎧
=−
=+
2
16
ba
ba
⎩
⎨
⎧
+=
=
2
142
ba
b
⎩
⎨
⎧
=
=
9
7
a
b
, тогда x = a
2
= 81, y = b
2
= 49.
Ответ: (81, 49).
2)
⎪
⎩
⎪
⎨
⎧
=+
=−
19
1
yx
yx
. Пусть
0,0 ≥=≥= byax
⎩
⎨
⎧
=+
=−
19
1
ba
ba
⎩
⎨
⎧
=
+=
182
1
b
ba
;
⎩
⎨
⎧
=
=
9
10
b
a
, где
ybxa == , , тогда х=100, у=81.
№ 1244
1)
⎪
⎩
⎪
⎨
⎧
−=+−
=−+
222
11
yyx
yx
()
⎩
⎨
⎧
+−=+−
=−+
1242
11
2
yyyx
yx
⎩
⎨
⎧
+−=+−−
−=
48422
2
2
yyyy
yx
⎩
⎨
⎧
=−
−=
064
2
2
yy
yx
()
⎩
⎨
⎧
=−
−=
0322
2
yy
yx
⎪
⎩
⎪
⎨
⎧
==
−=
2
3
,0
2
yy
yx
⎪
⎪
⎩
⎪
⎪
⎨
⎧
==
==
2
3
,0
2
1
,2
yy
xx
, при этом должно выполняться:
