Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие
Подождите немного. Документ загружается.

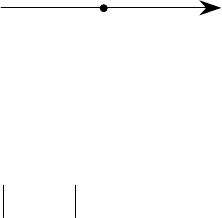
−
ε
окрестностью точки
0
x
называется интервал вида
()
ε
ε
+
−
00
, xx
,
0>
ε
.
ε
+
0
x
(
)
0
x
ε
−
0
x
x
Рис. 3
Точки x этого интервала удовлетворяют неравенствам:
ε
ε
+
<
<
−
00
xxx ;
ε
ε
<
−
<
−
0
xx
ε
<
−
0
xx
.
Пусть
X и Y числовые множества. Функцией из множества X во множе-
ство
Y называется правило, по которому каждому числу x из множества X од-
нозначно соответствует некоторое число
y из множества Y. Множество X на-
зывается
областью определения функции, множество Y называется обла-
стью значений.
Обозначения:
Y
X
f
→: ;
;YX
f
⎯→⎯
(
)
xfy
=
.
Пример:
1
2
+= xy
.
()
−∞+∞−= ,X
область определения;
[
)
−∞+= ,1Y
область значений.
Таблица элементарных функций
1.
−=
n
xy
степенная функция;
2.
()
−>= 0aay
x
показательная функция;
3.
−
= xy
a
log
логарифмическая
(
)
1,0
≠
> aa
;
.7
.6
.5
.4
−
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
=
=
=
;ctg
;tg
;cos
;sin
xy
xy
xy
xy
тригонометрические функции;
.11
.10
.9
.8
−
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
=
=
=
; arcctg
; arctg
;arccos
;arcsin
xy
xy
xy
xy
обратные тригонометрические функции.
Функции можно складывать, вычитать, перемножать, делить.

Пример.
1.
xxy sin2
2
⋅=
− функции
2
1
2xy =
и xy sin
2
=
перемножены;
2.
x
x
y
cos
2
= − функции
2
1
xy =
и
xy cos
2
=
поделены друг на друга.
Пусть даны две функции
(
)
xy
ϕ
=
и
(
)
yfz
=
:
Z
Y
X
f
⎯
→
⎯
⎯
→
⎯
ϕ
.
Сложной функцией
()
xFz = называется функция, имеющая областью опре-
деления X и областью значений Z, вычисляемая по правилу
()()
xfz
ϕ
=
.
Примеры:
1.
(
)
(
)
;sin,sin
22
yzxyxz ===
2.
()
(
)
;,sinsin
2
2
yzxyxz ===
3.
(
)
(
)
(
)
zuyzxyxu tg,log,logtg
2
33
2
==== .
§2. Числовые последовательности
Числовой последовательностью называется функция, областью опре-
деления которой является множество натуральных чисел
K,3,2,1
. Элементы
(члены) последовательности записываются в виде:
(
)
(
)
(
)
;,3,2,1 Kfff
или
{
}
;,,,
321
Kaaaa
n
=
или
{
}
K,,,
321
xxxx
n
=
Примеры:
1.
{}
⎭
⎬
⎫
⎩
⎨
⎧
=
n
a
n
1
, т.е.
K,
3
1
,
2
1
,1
321
=== aaa
2.
{} ( )
{
}
n
n
a 1−= , т.е.
.1,1,,1,1,1
20051321
=
−
=
−
=
=−= aaaaa K
3.
{}{}
1=
n
a , т.е. K,1,1
321
==
=
aaa
Последовательность
{}
n
a
называется
ограниченной, если существует число
М, такое, что
Ma
n
<
при всех
n
.
n
a
(
)
0
−
М
М
х
Рис. 4
Пример.
{}
{
}
−=
2
na
n
неограниченная последовательность.

Число a называется пределом последовательности
{
}
n
x
, если для лю-
бого числа 0>ε существует номер
N
, такой, что для всех
N
n ≥ выполняется
неравенство
ε<− ax
n
.
1
ε
а
2
ε
х
(
)
)
(
Рис. 5
Обозначение:
n
n
xa
∞→
= lim
.
Последовательность
{}
n
α
называется бесконечно малой (б. м.), если
0lim =
∞→
n
n
α
.
Пример:
()
0,
1
>
⎭
⎬
⎫
⎩
⎨
⎧
k
n
k
; K;
1
;
1
;
1
2
⎭
⎬
⎫
⎩
⎨
⎧
⎭
⎬
⎫
⎩
⎨
⎧
⎭
⎬
⎫
⎩
⎨
⎧
n
n
n
− б.м. последовательно-
сти
Свойства б. м. последовательностей:
1.
{}
−−⇔=
∞→
axax
nn
x
lim
б.м.
2. Если
{}
n
a
и
{}
−
β
n
б.м., то
{}
{
}
−
β
±
nn
a
б.м.
3. Если
{}
m
a
и
{}
−β
n
б.м., то
{}
{
}
−
β
⋅
nm
a
б.м.
4. Если
{}
−
n
a ограниченна,
{}
−
α
n
б.м., то
{
}
−
α
⋅
nn
a б.м.
Последовательность
{}
n
a
называется положительно бесконечно боль-
шой
(п. б. б.), если для любого числа М существует номер N, такой, что при
всех
N
n > выполняется неравенство
Ma
n
>
.
Обозначение:
+∞=
∞→
n
n
alim
(п. б. б.).
Пример 1.
{
}
−
2
n
п. б. б.
Последовательность
{}
n
a
называется
отрицательно бесконечно боль-
шой
(о. б. б.), если для любого числа М, существует номер N, такой, что при
N
n > выполняется неравенство
Ma
n
<
.
−∞=
∞→
n
n
alim
(о. б. б.)
Последовательность
{}
n
a
называется
бесконечно большой (б. б.) если
последовательность, составленная из величин
{
}
n
a
является п. б. б.
Пример 2.
(
)
{
}
−−
2
1 n
n
это не п. б. б., не о. б. б., а б. б. последователь-
ность.
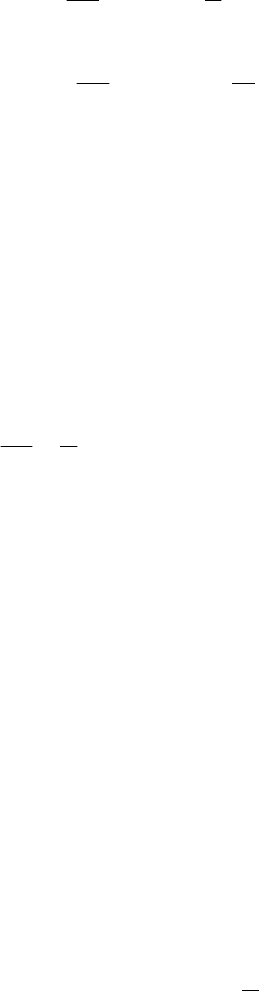
Обозначение:
∞=
∞→
n
n
alim
Т е о р е м а 1 (связь б.м. и б.б. последовательностей)
1) Если
{}
−
n
a б.м.,то
−
⎭
⎬
⎫
⎩
⎨
⎧
n
a
1
б.б.
⎟
⎠
⎞
⎜
⎝
⎛
∞=
0
1
.
2) Если
{}
−
n
a
б. б., то
−
⎭
⎬
⎫
⎩
⎨
⎧
n
a
1
б. м.
⎟
⎠
⎞
⎜
⎝
⎛
=
∞
0
1
.
Т е о р е м а 2. Если
∞
<
=
∞→
ax
n
n
lim
, то
{
}
−
n
x
ограничена.
Т е о р е м а 3. Если
ax
n
n
=
∞→
lim
,
bx
n
n
=
∞→
lim
, то ba
=
. (Если последова-
тельность имеет предел, то он единственный).
Т е о р е м а 4. Если ax
n
n
=
∞→
lim , by
n
n
=
∞→
lim то
1)
()
bayx
nn
n
±
=±
∞→
lim ;
2)
()
bayx
nn
n
⋅
=⋅
∞→
lim
;
3) При 0≠b ,
b
a
y
x
n
n
n
=
∞→
lim ;
4)
()
n
n
n
n
xccx
∞→∞→
= limlim
, где
cons
t
c = .
Т е о р е м а 5. Если
ax
n
n
=
∞→
lim
,
by
n
n
=
∞→
lim
, причем
nn
yx <
при всех
n
,
то .ba ≤
Т е о р е м а 6. (о двух милиционерах)
Если
nnn
yzx ≤≤
при всех
n
и
ayx
n
n
n
n
=
=
∞→∞→
limlim
, то
az
n
n
=
∞→
lim
.
Последовательность
{}
n
x , для которой выполняется неравенство
K≤≤≤
321
xxx называется возрастающей.
Последовательность
{}
n
x для которой выполняется неравенство
K≥≥≥
321
xxx
называется убывающей.
Такие последовательности называются
монотонными.
Т е о р е м а. Всякая монотонная ограниченная последовательность
имеет предел.
Рассмотрим последовательность
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
+
n
n
1
1
.
Эта последовательность обладает свойствами:
1) возрастает,
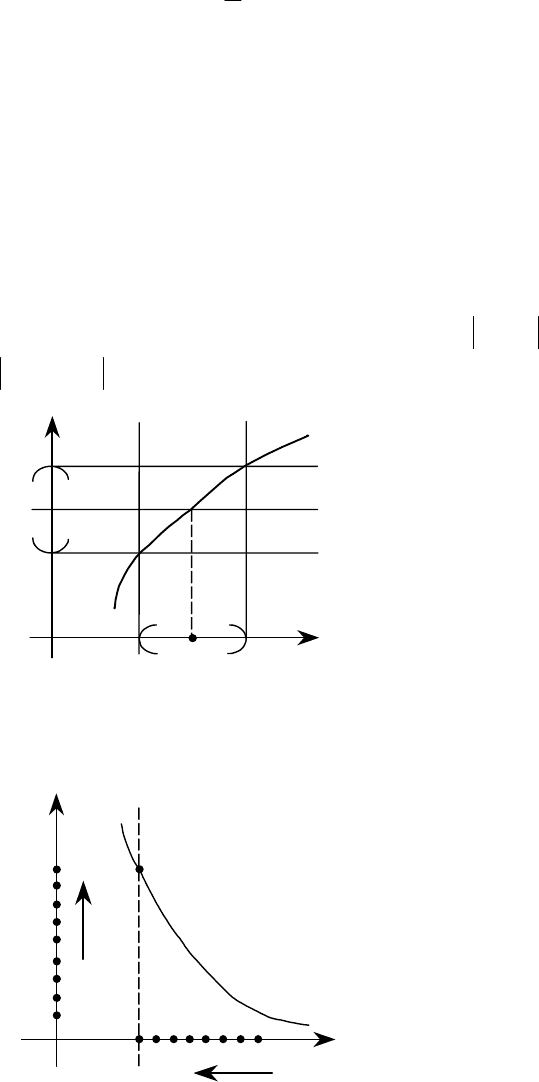
2) ограниченна (заключена в интервале
(
)
3,2
), поэтому она имеет предел, ко-
торый обозначим е;
K7,2≈e
Т.е.
e
n
n
n
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
1
1lim
(
−
e
основание натурально-
го логарифма
xx
e
lnlog = ;
−
x
e экспонента).
§3. Предел функции
Пусть
(
)
−= xfy определена в некоторой окрестности точка а, кроме,
может быть, самой точки а.
Число А называется
пределом функции
(
)
xfy
=
в точке а (или при
a
x
→
), если для любого числа 0>
ε
, существует число 0>
δ
(зависящее от
ε
), такое, что при всех х, удовлетворяющих неравенству
δ
<−< ax0
вы-
полняется неравенство
()
ε
<
− Axf
.
а
δ
δ
y
А
ε
ε
0
(
)
xfy
=
Рис. 6
Обозначение:
()
xfA
ax→
= lim
.
Можно использовать ещё одно определение предела функции.
А
y
a
x
{}
n
xf
{
}
n
x
(
)
xfy
=
Рис. 7
Число А называется пределом функции
(
)
xfy
=
в точке а, если для
любой последовательности
{
}
n
x , такой, что
ax
n
n
=
∞→
lim
выполняется:
(){}
Axf
n
n
=
∞→
lim
.Если для любой последовательности
{
}
n
x такой, что
ax
n
n
=
∞→
lim
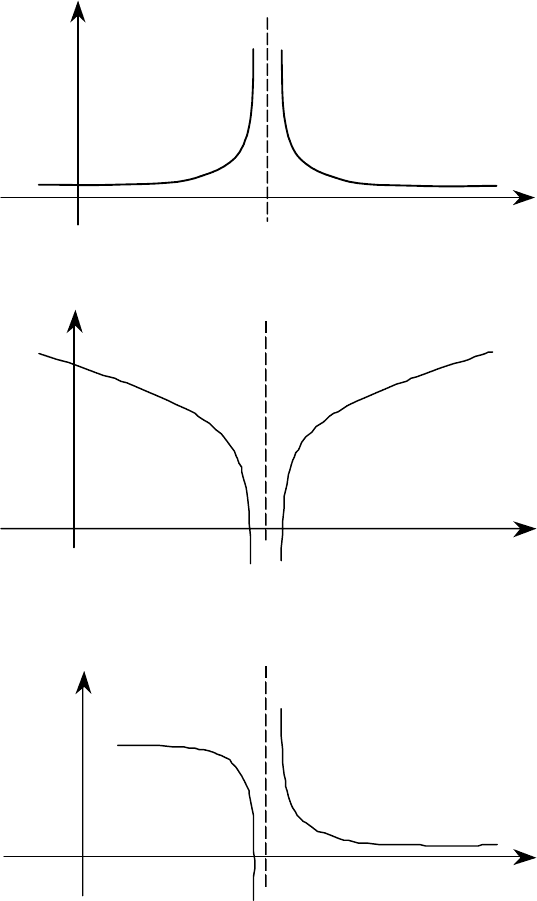
1)
(){}
n
xf − п. б. б., то
()
+
∞
=
→
xf
ax
lim
(предел функции равен ∞+ );
a
x
y
Рис.8
2)
(){}
xf
− о. б. б., то
()
−
∞
=
→
xf
ax
lim
(предел функции равен
∞
−
);
a
x
y
Рис. 9
3)
(){}
xf
− б. б., то
()
∞
=
→
xf
ax
lim
(предел функции равен
∞
).
a
x
y
Рис. 10
Т е о р е м а 1 (основные свойства пределов функции).
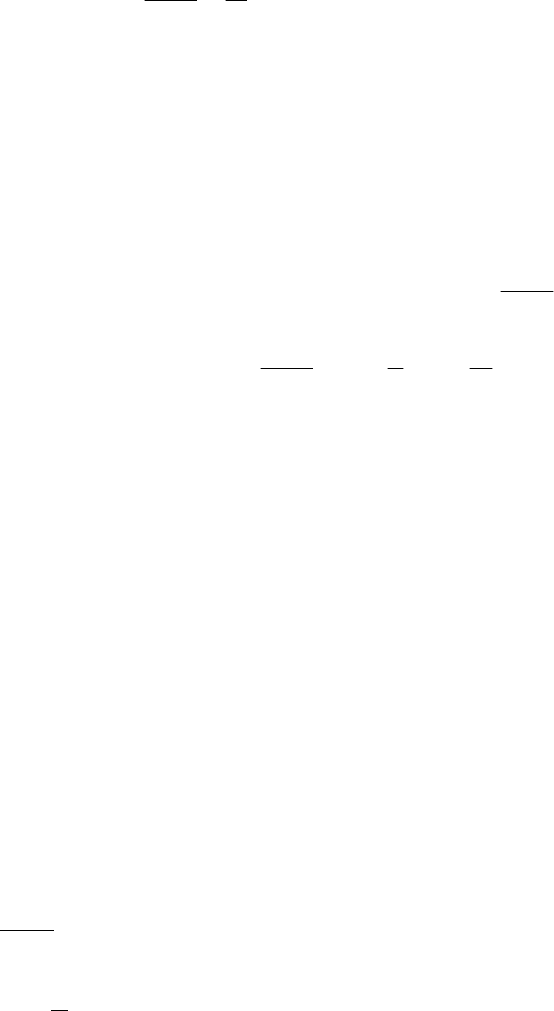
Пусть
(
)
Axf
ax
=
→
lim
,
(
)
Bxg
ax
=
→
lim
, тогда:
1)
() ()()
BAxgxf
ax
±
=
±
→
lim
;
2)
() ()()
BAxgxf
ax
⋅
=
⋅
→
lim
;
3) Если 0
≠B ,
()
()
B
A
xg
xf
ax
=
→
lim ;
4)
()()
ACxfС
ax
⋅
=⋅
→
lim
, где
−
С
число.
Т е о р е м а 2. Если в некоторой окрестности точки а выполняется не-
равенство
()
(
)
xgxf ≤ и
()
Axf
ax
=
→
lim ,
(
)
Bxg
ax
=
→
lim , то
B
A
≤
.
Т е о р е м а 3. Если в некоторой окрестности точки а выполняется не-
равенство
()
(
)()
xgxxf ≤≤
ϕ
и
(
)
(
)
Axgxf
axax
=
=
→→
limlim
, то
()
Ax
ax
=
→
ϕ
lim
.
Т е о р е м а 4. 1) Если
(
)
0lim
=
→
xf
ax
, то
()
∞=
→
xf
ax
1
lim
.
2) Если
()
∞
=
→
xf
ax
lim
, то
()
0
1
lim =
→
xf
ax
.
⎟
⎠
⎞
⎜
⎝
⎛
=
∞
∞=
0
1
;
0
1
.
Предел функции может быть определен на бесконечности и может рав-
няться бесконечности.
1) Если для любой
{}
n
x
− п.б.б.,
(
)
{
}
,lim Axf
n
n
=
∞→
то
()
Axf
n
x
=
+∞→
lim
(предел
()
xf
на
∞+
равен
A
).
2) Если для любой о. б. б.
{}
n
x
(
)
{
}
,lim Axf
n
n
=
∞→
то
()
Axf
n
x
=
−∞→
lim
(предел
()
xf на ∞− равен
A
).
3) Если для любой п. б. б. последовательности
{
}
n
x
последовательность
(){}
xf как же п. б. б., то
(
)
+
∞
=
+∞→
xf
x
lim
.
Упражнение. Написать варианты определений:
()
±∞=
±∞→
xf
x
lim
.
§4. Замечательные пределы
Полезно знать следующие пределы
1)
1
sin
lim
0
=
→
x
x
x
− первый замечательный предел;
2)
e
x
x
x
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
1
1lim
− второй замечательный предел;
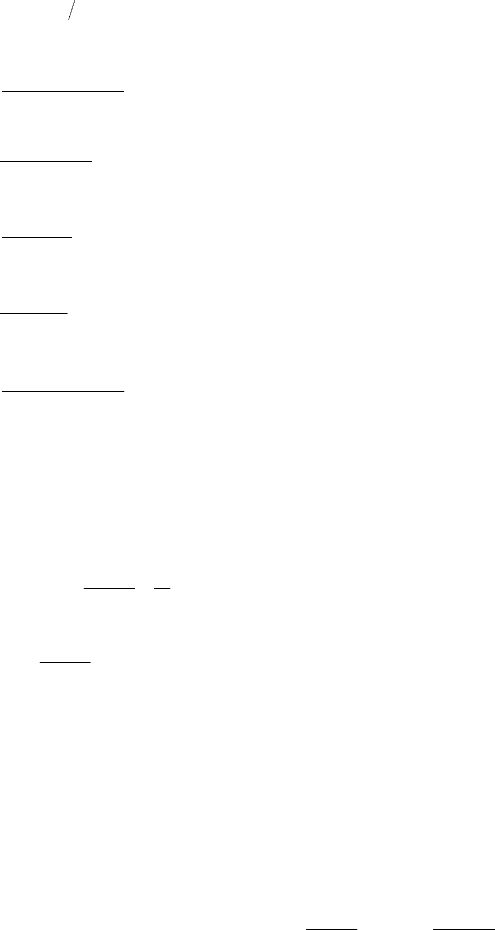
()
ex
x
x
=+
→
1
0
1lim ;
3)
()
e
x
x
a
a
x
log
1log
lim
0
=
+
→
;
()
1
1ln
lim
0
=
+
→
x
x
x
− частный случай;
4) a
x
a
x
x
ln
1
lim
0
=
−
→
;
1
1
lim
0
=
−
→
x
e
x
x
− частный случай;
5)
()
n
x
x
n
x
=
−+
→
11
lim
0
.
Функция
(
)
x
α
называется бесконечно малой в точке
a
, если
()
0lim =
→
x
ax
α
(б.м).
Рассмотрим
()
x
α
и
()
x
β
− две б. м. функции в точке a и предел их от-
ношения
()
()
⎟
⎠
⎞
⎜
⎝
⎛
β
α
→
0
0
lim
x
x
ax
.
Если
()
()
0lim ≠=
β
α
→
c
x
x
ax
, то
()
x
α
и
(
)
x
β
называются б. м. одного и того же по-
рядка малости
в точке а.
Если 1=с , то
(
)
x
α
и
()
x
β
называются эквивалентными в точке а
() ()
xx
ax
βα
→
~
.
Т е о р е м а. (Использование эквивалентности б. м.). Если
()
(
)
xx
1
~ αα
() ()
xx
1
~ ββ при
a
x
→
, то
(
)
()
(
)
()
x
x
x
x
axax
1
1
limlim
β
α
=
β
α
→→
.
Таблица эквивалентных функций
1)
αα
→α 0
~sin
2)
α
α
→α 0
~tg
3)
αα
→α 0
~arcsin
4)
α
α
→α 0
~arctg
5)
()
αα+
→α 0
~1ln
6)
α−
→α
α
0
~1e
7)
()
α−α+
→α
n
n
0
~11
8)
aa ln
~
1
α
−
α

Пример 2.
33lim
2
3
2
1
lim
2
131
lim
0
0
2
13sin1
lim
000
===
⎟
⎠
⎞
⎜
⎝
⎛
−+
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
→→→
x
x
x
x
x
tg
x
xxx
.
Если
()
()
0lim =
x
x
β
α
, то
()
x
α
называется б. м. более высокого порядка мало-
сти
чем
()
x
β
в точке
a
.
Если
()
()
∞=
→
x
x
x
β
α
α
lim
, то
()
x
α
называется б. м. более низкого порядка малости
чем
()
x
β
в точке
a
.
Если
()
()
x
x
x
β
α
α
→
lim
не существует, то
(
)
x
α
и
(
)
x
β
называются несравнимыми.
§5. Непрерывность функции в точке
Функция
()
xfy = называется непрерывной в точке а, если она опре-
делена в некоторой окрестности точки
a
и
(
)
(
)
afxf
ax
=
±→
lim
.
Пределы
справа и слева:
() ()
−=
+→
>
→
xfxf
ax
ax
ax
limlim
предел справа;
() ()
−=
−→
>
→
xfxf
ax
ax
ax
limlim
предел слева.
Пределы справа и слева могут отличаться
a
x
y
A
B
(
)
Axf
ax
=
+→
lim
()
Вxf
ax
=
−→
lim
B
A
≠
Рис. 13
а
Рис. 11
а
Рис. 12

Дадим развёрнутое определение непрерывности
Функция
(
)
xfy =
является непрерывной в точке а, если
1) определено значение функции в точке а;
2) существуют конечные односторонние пределы
(
)()
xfxf
axax −→+→
lim;lim
;
3) эти пределы равны между собой
(
)
(
)
xfxf
axax −→+→
=
limlim
;
4) они равны
()
(
)
(
)
afxfxf
axax
=
=
−→+→
limlim
.
a
x
y
(
)
аf
Рис. 14
Свойства непрерывных функций
Т е о р е м а 1. Если
()
xf
и
(
)
xg
непрерывны в точке а, то
1)
() ()
xgxf ±
− сумма (разность) непрерывна в точке а;
2)
() ()
xgxf ⋅
− произведение непрерывно в точке а;
3)
()
()
−
xg
xf
отношение непрерывно в точке а
, если
(
)
0
≠
ag
.
Т е о р е м а 2. (непрерывность сложной функции). Если
()
xy
ϕ
= не-
прерывна в точке а
и
()
yfz =
− непрерывна в точке
()
ab
ϕ
=
, то сложная
функция
()()
−= xfz
ϕ
непрерывна в точке а.
Т е о р е м а 3.
Все элементарные функции непрерывны в своей области
определения.
§6. Точки разрыва графика функции и их классификация
Точка, в которой нарушено хотя бы одно из четырех условий непре-
рывности называется
точкой разрыва функции. Точка а называется точкой
разрыва
первого рода, если условие 2) непрерывности функции не нарушено.
Графики функций с разрывами 1 рода имеет вид
