Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

14.10. Mobility in an Unstable Population 365

timing in this crude representation involves the 17 years from the start

of the baby boom to college entry of the larger cohorts, plus the 8 years

through college and graduate school, a total of 25 years from the ﬁrst rise

in births to the start of an employment crisis for Ph.D.s. Twenty-ﬁve years

is about the interval from the later 1940s to the early 1970s.

14.10 Mobility in an Unstable Population

The mobility model of Section 5.8 exhibited the demographic factor in

promotion, ﬁnding it faster for members of populations in rapid growth

than for members of stationary populations. A person will get to a middle-

level position about 9 years earlier in the fastest growing population than

in a stationary one. Mortality also helps (at least for those who survive) but

much less; a very high mortality population (

= 35 years) will advance

its surviving members to middle positions only 2 to 3 years sooner than the

lowest mortality population known (say

= 75 years). High subsequent

birth rates advance a person’s promotion more than do high death rates.

The above results are comparative rather than dynamic—they compare

the age of attaining a given level in a fast- and in a slow-growing population,

but supposing for each that its rates have been ﬁxed and continuing over

a long period. A separate question concerns the slowing down of an actual

population: what diﬀerence does it make to individuals now alive that the

United States was growing at 1.5 percent per year in the late 1950s and

is dropping from this rate toward stationarity? Stable population theory,

assuming as it does ﬁxed rates, cannot by its very nature answer a question

about the eﬀect of change in rates over time.

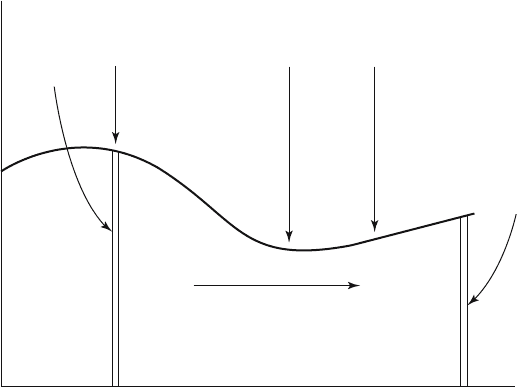
As an introduction to the problem consider the United States age distri-

bution, as of the mid-1970s, in the stylized version of Figure 14.3. Those

approaching retirement at that time were members of the large cohorts

born in the 1920s and earlier. The working population then in its forties

consisted of the very small cohorts born in the 1930s, and new entrants up

to 1975 had been larger, steadily increasing toward the left in Figure 14.3,

up to those born about 1960. Following that came a downturn, so that the

new entrants of the 1980s were fewer and decreasing.

Those in their forties at the time of this diagram were fortunate in two

distinct ways. They were called on to replace the large number of their

elders retiring from senior posts, and they had been drawn upward by the

large number of new entrants who were younger than themselves. Super-

visors and teachers are required in relation to workers and students; the

tests of competence for supervisors and teachers are less stringent in times

when more are required.

Thus those born in the 1930s, having been pushed upward by the young

people coming in behind them, could look forward to further promotion

366 14. Some Types of Instability

20 40 50 65

Age in 1975

Number of persons

Retirements

Entrants

1955

Birth year

1935

1925

Figure 14.3. Stylized representation of the supply of labor in the United States.

as their seniors retired. However, those born at the peak of the baby

boom in the 1950s and early 1960s would never in their later careers be in

such great demand as supervisors and teachers, for they were followed by

sparse cohorts, nor were they drawn up as strongly to ﬁll posts vacated by

retirement, because these were less numerous.

14.11 The Easterlin Eﬀect

The high United States fertility of the 1950s and the subsequent decline

have puzzled observers who believe that there are strong economic de-

terminants of age-speciﬁc fertility. The phenomenon could not be due to

prosperity, since income in the 1950s was not as high as in the 1960s. That

children are positively related to income in time series did not seem to help

here, until Easterlin (1961, 1968, 1980) noted that the prosperity of couples

of childbearing age is what we should look for, not general prosperity. He

pointed out that couples of childbearing age in the 1950s, born between the

humps of the 1920s and the 1940s, were located in a hollow similar to that of

Figure 14.3. Not only was their promotion relatively rapid, but also in any

one position, insofar as there is age complementarity in production, they

frequently had the advantage of meeting situations in which they were too

few to do the necessary work, with resulting appreciation of their services.

This was often expressed in material terms and resulted in high wages and

good prospects relative to what people of their age would have been paid

in a diﬀerent age conﬁguration; hence these people have enjoyed a sense

14.11. The Easterlin Eﬀect 367

of security and well-being. Their conﬁdence is well founded, for they will

spend their whole working lives in the same advantageous position. They

have translated their advantage into childbearing, perhaps projecting their

security into the next generation and feeling that their children will be in

demand just as they are. Macunovich (1998) has compiled a detailed review

of studies on the fertility patterns predicted by Easterlin’s hypothesis.

So strong was this eﬀect in the 1950s that it entirely reversed the ten-

dency of the classical model with ﬁxed age-speciﬁc rates of Chapter 6.

Instead of a dip, echoing that of the 1930s, the 1950s showed births at the

highest level in half a century. The 1930s gave a relative advantage to their

children by producing few of them, and these later repaid the advantage

by having many children. Such a mechanism could produce a very stable

result if the rise in birth rates was of just the right amount to compensate

for the few parents. In the actual case, however, the rise overcompensated.

The subsequent steady fall of the birth rate in the 1960s might well have

been due to the entry into childbearing ages of the large cohorts born in

the 1940s. If this was the dominant mechanism operating, we can predict

continued low birth rates at least through the 1970s. Not until about 1990

will the parental generation again be small enough to be encouraged to have

large families. Instead of the waves of generation length in the free response

of the demographic model we ﬁnd waves two generations in length.

To translate this into quantitative terms we consider females only, and

simply suppose that all children are born at the same age of parent, say 25

years or the mean length of generation. If the “normal” female growth ratio

is R

per generation, births in the tth generation are B

= R

t−1

.The

conditions imply geometric increase and lead to the solution B

= B

Suppose now that superimposed on this is a component of births in the

tth generation that depends on how small is the number of couples aged 25

compared with the number of couples aged 50. When the couples aged 25

are relatively few, that is to say, when B

t−1

is less than its “normal,” sup-

pose an additional γ(R

t−2

−B

t−1

)birthsinthet generation, γ positive.

These conditions mean that the sizes of cohorts are related by

= R

t−1

+ γ (R

t−2

− B

t−1

) , (14.11.1)

where R

is no longer necessarily the net reproduction rate.

To solve (14.11.1) we try B

= x

and ﬁnd

− (R

− γ) x − γR

=0, (14.11.2)

of which the roots are conveniently x = R

and −γ. Thus the solution of

(14.11.1) is

= k

+ k

(−γ)

, (14.11.3)

where k

and k

depend on the initial conditions. The term in (−γ)

tells

us that cycles will be generated two generations in length. If the factor for

normal increase R

is greater than γ, any waves once started will diminish

368 14. Some Types of Instability

as a proportion of the geometric increase. If γ is less than unity, they will

diminish absolutely.

Lee (1968) applied Easterlin’s theory in a much more reﬁned model,

one recognizing individual age groups. He also traced out its historical

antecedents, starting with a quotation from Yule (1906):

If ... the supply of labour be above the optimum, the supply

of labour being in excess, the birth rate will be depressed, and

will stay depressed until the reduction begins to have some eﬀect

on the labour market. But this eﬀect will not even commence

for ﬁfteen or twenty years, and the labour supply may not be

adjusted to the demand for, say, thirty years. The birth rate

may now have risen again to normal, but the labour supply will

continue to fall owing to the low birth rates formerly prevalent.

The birth rate will therefore rise above normal and continue

above normal so long as the labour supply is in defect, and so

matters will go on, the population swinging about the optimum

value with a long period of perhaps ﬁfty to one hundred years,

and the birth rate following suit.

The germ of this idea is to be found as far back as Adam Smith, who

considered that the supply of labor, like the supply of shoes, was determined

by demand. Smith did not go the one further step of recognizing that the

period of production of labor is longer than the period of production of

shoes, with resulting longer and deeper cycles.

The Easterlin hypothesis is an example of a nonlinear demographic

model, in which the vital rates are functions of the population itself

(“density-dependence” in ecological terminology; see Lee (1987) for a de-

tailed discussion of density eﬀects in human demography). Such models can

generate instability in the form of nonstationary solutions: cycles, quasi-

periodicity, and chaos. Such analyses are beyond the scope of this book,

but general discussions can be found in Cushing (1998) and Chapter 16 of

MPM. Nonlinear phenomena, many of them remarkably subtle, have been

beautifully documented in careful laboratory experiments on populations

of the ﬂour beetles of the genus Tribolium (Cushing et al. 2003).

In the case of human populations, a series of analyses followed Lee’s

(1974) study of the Easterlin eﬀect (Frauenthal and Swick 1983, Wachter

and Lee 1989, Wachter 1991, Chu 1998). Cyclic dynamics are clearly possi-

ble from the model, but whether parameters estimated from United States

demographic data can produce them is not clear.

Some apology is needed for the heterogeneous material contained in the

present chapter, which reﬂects the fact that populations can be unstable in

many diﬀerent ways. To write about stable theory in a coherent fashion is

bound to be more straightforward than to attempt to write about every-

thing that is not stable theory. Furthermore, the range of applications here

attempted or recounted is especially wide, including estimating the rate

14.11. The Easterlin Eﬀect 369

of increase of a population when its death rate or its birth rate is falling,

backward projection under instability, ﬁnding the time to stability after a

disturbance, old-age pensions under reserve and nonreserve systems, and

the consequences for the educational system, the labor market, and the

birth rate of the baby boom and its aftermath.

The Demographic Theory of Kinship

This chapter will extract information on kinship numbers from the age-

speciﬁc rates of birth and death of a population. A ﬁxed set of age-speciﬁc

rates implies the probability that a girl aged a has a living mother and

great-grandmother, as well as her expected number of daughters, sisters,

aunts, nieces, and cousins. Certain assumptions are required to draw the

implications, some stronger than others. The formulae of this chapter in

eﬀect set up a genealogical table, giving not the names of incumbents in

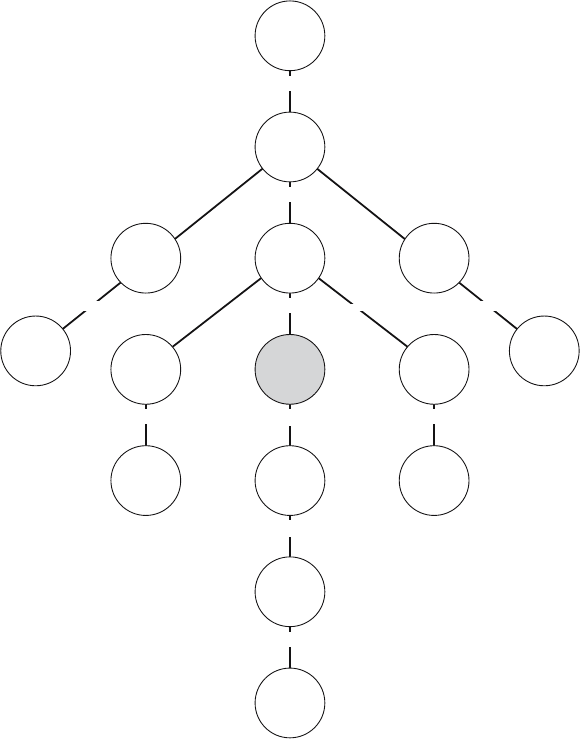
the several positions but the expected number of incumbents. Those of

Figure 15.1 are based on birth and death rates of the United States in

1965, whose net reproduction rate R

was 1.395 and

was 73.829, all

for females. They oﬀer a diﬀerent kind of knowledge from what would be

provided by a kinship census.

Like earlier chapters, this one supposes a population generated by birth

and death with overlapping generations. (Generations do not overlap in

annual plants, where all the parents have disappeared before the children

come to life. This circumstance requires population models that account

for processes both within and between years; see MPM Section 13.2.) The

considerable longevity of human beings, as well as other large mammals

and long-lived birds, after the birth of their oﬀspring produces simultane-

ously living kin of many kinds—not only parents and children, but also

grandparents, nephews, and cousins. Human beings produce most of their

oﬀspring in births of discrete individuals, but this is not recognized in the

present analysis, which supposes m(x) dx of a daughter in each dx of ma-

ternal age. For certain kin this introduces serious qualiﬁcations, speciﬁed

in Section 15.3. Development of this ﬁeld is due to Lotka (1931), Burch

15. The Demographic Theory of Kinship 371

0.000

0.112

1.370

0.780

0.788

0.713

0.986

0.581

0.924

0.849

0.620

0.339

0.156

0.000

Great–granddaughters

Great–grandmother

Grandmother

Mother

Ego

Older sisters Younger sisters

DaughtersNieces through

older sisters

Nieces through

younger sisters

Granddaughters

CousinsCousins

Aunts younger than motherAunts older than mother

Figure 15.1. Expected number of female kin alive when Ego (hatched circle) is

aged 40, based on birth and death rates of the United States, 1965.

(1970), Coale (1965), Goodman, Keyﬁtz, and Pullum (1974) and Le Bras

(1973).

Explicit recognition of the several degrees of living and dead kin varies

from one culture to another, and indeed from one family to another. We

disregard here cultural, social, and psychological deﬁnitions and deal with

numerical relations among average numbers of biological kin as they are

determined by birth and death rates. To avoid undue complication, all of

the following discussion recognizes female kin only.

372 15. The Demographic Theory of Kinship

15.1 Probability of Living Ancestors

Deterministic models concern both population numbers and probabilities.

The two perspectives are at least on the surface distinct.

Counting Method. A large population can be seen as developing according

to given rules, and in eﬀect we can make counts of the number of individuals

having the kin relations of interest. This is an extension of the notion that

is the number of births occurring at one moment and l(x)isthenumber

of those surviving x years later, the cohort conception of the life table l(x)

referred to in Section 2.1. (But we still keep l

=1.)

Probability Method. We can start by thinking of an individual and work out

probabilities and expected values for his various kin. This is an extension

of the interpretation of the life table l(x) as the probability that a child

just born will survive for x years.

15.1.1 Living Mother by the Counting Method

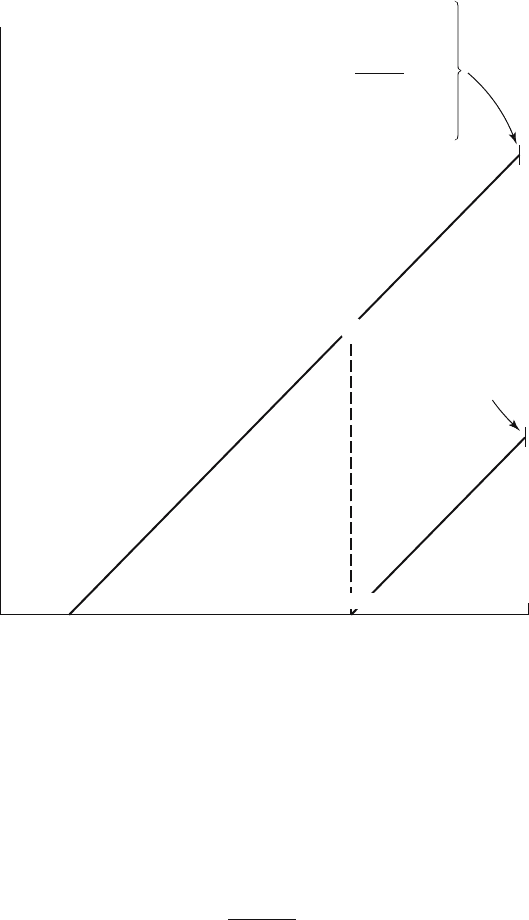
Our ﬁrst approach to ﬁnding the probability that a girl aged a has a living

mother is to see how a population would have developed starting from B

girl children born at a moment a + x years ago. At age x of this maternal

generation cohort the survivors were Bl(x), and during the interval x to

x + dx they could be expected to give birth to Bl(x)m(x)l(a) dx daughters

who would live to age a. Of the mothers who gave birth at age x afraction

l(x + a)/l(x) would survive over an additional a years; hence the number

of living mothers must be Bl(x)m(x) dx[l(x + a)/l(x)]l(a). A woman is

counted once for each birth that survives.

All this concerns one cohort of the mother generation. But we seek the

probability that a girl aged a, standing before us, has a living mother,

without any knowledge of which cohort her mother belonged to, or indeed

any knowledge other than the regime of mortality and fertility supposed

to apply to all generations and at all times. If births as a function of time

are B(t), and the present is time t, girls born x + a years ago numbered

B(t − a −

x), and the number of living mothers (counted once for each

daughter) of all cohorts who gave birth to girls now alive and a years of

age is the integral



B(t − a − x)l(x)m(x)

l(x + a)

l(x)

l(a) dx. (15.1.1)

For the same birth function B(t) the number of daughters, that is, girls

born a years ago and surviving to the present, is

B(t − a)l(a). (15.1.2)

Hence the average number of mothers per daughter at time t is the ratio

of (15.1.1) to (15.1.2).

15.1. Probability of Living Ancestors 373

Time

t – a

Time

t – a – x

Bl (x) m (x) dx

B(t – a)l (a)

Surviving daughters

Bl (x)

B(t – x – a)l (x + a) (Total

women aged x + a, of whom

B(t – x – a)l (x) m(x) l (a) dx

are surviving mothers of

surviving daughters)

l(x + a)

l(x)

Figure 15.2. Cohort of mothers giving birth at age x, and of daughters born at

age x of mother.

Now, if the age-speciﬁc rates of birth and death have been in eﬀect for a

long period of time, the births will be growing exponentially, say according

to the curve B

,wherer is determined by (6.1.2). Entering this for the

birth function in each of (15.1.1) and (15.1.2), taking the ratio of the ﬁrst to

the second, and canceling l(a)B

r(t−a)

from numerator and denominator

gives

(a)=



l(x + a)

l(x)

−rx

l(x)m(x) dx (15.1.3)

for the probability that a girl aged a has a living mother under the given

regime of mortality and fertility (Lotka 1931).

All of the problems of this chapter can be solved in this way, by following

cohorts through time, then in eﬀect taking a census at a certain moment,

and ﬁnding the ratio of one census aggregate to another. This does not of

374 15. The Demographic Theory of Kinship

course constitute a census of the real population, which would show the

result of changing death rates over time, but is at best a simpliﬁed ab-

stract argument devised by analogy to counting population by means of

a census and births by means of registrations. Made possible by the de-

terministic assumption of Section 2.1, it requires no explicit considerations

of probability, yet it is both unnecessarily complicated and unnecessarily

restricted.

15.1.2 Living Mother by Conditional Probability

Alternatively, the life table l(x) column is taken, not as a cohort, but as

the probability of living to age x for a child just born, on the regime of

mortality assumed, with l

= 1. The corresponding approach will provide

a result for M

(a) identical with (15.1.3).

In seeking the probability that a girl chosen at random out of a popu-

lation with birth rates m(x) and survivorship l(x) has a living mother, we

ﬁrst note that the conditional case is easily solved. If the mother was a

known x years old when she gave birth to the girl, then the chance that

the mother is alive a years later must be l(x + a)/l(x). This probability,

conditional on the mother’s age at bearing the girl having been x,isthe

ﬁrst part of the solution.

It remains to remove the condition, which is not part of the problem; we

do not care about the age x of the mother at childbearing. To eliminate the

condition we average over all ages x, giving each x a weight proportional

to the number of births occurring at that age of mother under the regime

in question. The number of the stable population of ages x to x + dx per

current birth is e

−rx

l(x) dx, from Euler’s argument of Section 5.1, and the

births to this fraction are e

−rx

l(x)m(x) dx, still taken per one current birth.

The last expression is the fraction of births occurring to women aged x to

x + dx; once again, its total over all x is unity by the (6.1.2) deﬁning r.

Hence the unconditional probability that the mother of the girl in question

is still alive is obtained by multiplying e

−rx

l(x)m(x) dx by the survivorship

l(x + a)/l(x) and totaling over all x.

This is the same expression, derived more compactly, that we obtained

as (15.1.3). Because of its compactness the probability method will be pre-

ferred in what follows. Note that (15.1.3) is more general than appeared

in our interpretation. The derivation did not require the fact that the girl

born a years ago is still alive, but consisted in ﬁnding the probability of

survival of the mother a years after a random birth. Whether the girl born

survived does not aﬀect the value of M

(a), given independent regimes.

15.1.3 Probability of Living Grandmother

Now think of the grandmother of the girl aged a; we once again provisionally

take the latter as having been born at age x of her mother. The grandmother