Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

Some Types of Instability

A population can be stable in only one way: by the constancy of its birth

and death rates over time, and hence the constancy of its rate of increase.

It can be unstable in inﬁnitely many ways: by falling or rising birth rates,

by falling or rising death rates, by either birth or death rates rising at some

ages and falling at others, by the rise or fall being moderate or rapid, by

its being linear, quadratic, or of higher degree. Any and all of these and

their combinations could be given the same detailed attention as stability.

Needless to say that will not be done here, nor is it likely to be done

anywhere else.

The stable model has been studied in detail because it is more informative

than any single case of instability. The diversity of kinds of instability

distracts attention from the interest in any one kind. To keep down the

complexity in the treatment here, either fertility or mortality will be allowed

to vary, but not both, and populations will be assumed to be closed to

migration as before.

Falling death rates are conspicuous in most of the world today; our ﬁrst

task is to see how their recognition alters the stable model of Chapter 5.

14.1 Absolute Change in Mortality the Same at

All Ages

Coale (1963) opened up this subject by analyzing the eﬀects of a steady

fall in death rates; he called quasi-stable a population in which birth rates

336 14. Some Types of Instability

remain constant while death rates decline uniformly. The quantitative eﬀect

of this on rates of increase from the stable model was calculated by Coale

and Demeny (1967). The following is an attempt to see the eﬀect in general

terms. In the ﬁrst example death rates rise or fall by the same absolute

amount at all ages. This is hardly realistic, but it will show the approach.

Suppose a rise each year at all ages equal to the constant k (which would

be negative to provide for a fall, say of magnitude 0.0001, in which case

k = −0.0001; the constant k is restricted to values that leave probability

positive and less than 1 at all ages). After n years the mortality of age

a will not be µ(a), as it was at the beginning, but µ

∗

(a)=µ(a)+nk.

If the initial probability of survivorship was l(x)=exp[−



µ(a) da], the

survivorship r years later, subject to µ

∗

(a)=µ(a)+nk, will be l

∗

(x)=

exp{−



[µ(a)+nk] da} = l(x)e

−nkx

. This is true whether both the initial

µ(a) and the subsequent µ(a)+nk apply to periods or to cohorts.

14.1.1 Inferring the Increase in Births

Apply the cohort case to an observed age distribution to ascertain the rate

of increase in births. If k = 0, the stable assumption for ascertaining the

rate of increase in the population from a census, derived as (5.2.4), gives

y − x

log



B(t − x)

B(t − y)



y − x

log





, (14.1.1)

where the c

and c

are the fractions in ﬁnite intervals around ages x and

y (Figure 14.1) and are to be identiﬁed with observed populations. This

is modiﬁed to estimate the increase in births between y and x years ago

y>x, (once we abandon stability, we have to specify the time to which

the rate of increase refers). If death rates increase at k per year between

cohorts, and the life table for the cohort born y years ago is given by µ(a)

and that for the cohort born x years ago µ

∗

(a)=µ(a)+k(y − x), then

∗

= l

−k(y−x)x

, and the estimate becomes

y − x

log



∗



y − x

log



−k(y−x)x



= r

+ kx,

(14.1.2)

on simplifying and expressing the result in terms of (14.1.1).

For y>xand falling mortality (i.e., k<0), we have r

 r

. In words,

under a regime of falling mortality use of the customary formula (14.1.1),

which assumes a ﬁxed life table, gives a rate of increase in the earlier

births that is too high by −kx, the fall in mortality since the younger age

group was born. The usual formula (14.1.1) gives too high an r because it

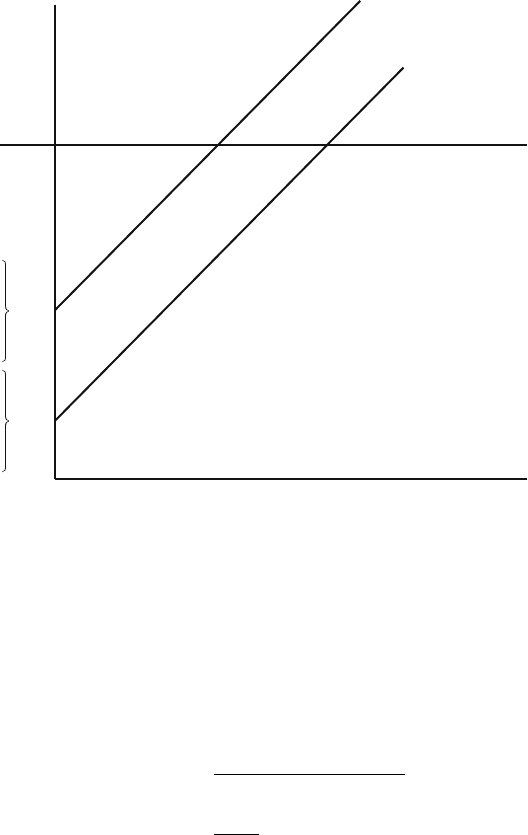
14.1. Absolute Change in Mortality the Same at All Ages 337

Time

Census date

Birth date

of those

aged x

at census

Birth date

of those

aged y

at census

Age

t – x

txy

t – y

␮*(a); l*(a)

␮(a); l(a)

Figure 14.1. Lexis diagram showing census date and comparison of those

enumerated at age x and y to ascertain increase between x and y years ago.

disregards the fact that the younger age with the life table l

∗

originates in

fewer births than the life table l

implies.

Let us generalize this to ﬁnd the average rate of increase in persons

aged z between the y cohort and the x cohort, where x<z<y.Thec

projected back to age z number c

), and the c

projected forward

to age z number c

−k(y−x)(z−x)

). The average rate of increase r

found from

exp[r

(y − x)] =

−k(y−x)(z−x)

)

−k(y−x)(z−x)

or, on solving for r

= r

− k(z − x), (14.1.3)

which reduces to (14.1.2) for z =0.Fork negative, the increase in any age

z greater than x will be more rapid than r

, the rate inferred on the stable

model. [Show that the result applies to any z, whether or not it is between

x and y.]

338 14. Some Types of Instability

Increase in Person-Years in Cohort. To proceed from how persons aged z

were changing over some particular interval to rate of increase in popula-

tion, a ﬁrst approach is to compare person-years in the two cohorts that

are x and y years of age, respectively, at time t. Person-years in a cohort

are births times expectation of life, that is to say, births times the integral

of the survivorship function. This is not the usual way to estimate pop-

ulation increase, but is worth starting with because of its mathematical

convenience. [Prove that the estimate of change is approximately

≈ r

− k(¯a − x), (14.1.4)

where ¯a is the mean age.]

14.2 Proportional Change in Mortality

Now instead of a ﬁxed change k at all ages suppose a fractional change—

that mortality for a given cohort (or period) is µ(a), while n years later

it is µ

∗

(a)=µ(a)(1 + nk). Then that later cohort (or period) will have

survivorship l

∗

= l

1+nk

.Ifk<0, then l

∗

Rate of Increase of Births. From the numbers c

enumerated at time t

and age y the births B(t − y)mustbeB(t − y)=c

, again taking as

the standard life table the cohort passing through age y at census time t.

The table for the younger cohort aged x at the census must have µ

∗

(a)=

µ(a)(1 + nk), so its survivorship to age x will be l

∗

= l

1+nk

= l

1+(y−x)k

Then the number of births B(t −x) from which the c

are the survivors is

B(t − x)=

∗

1+(y−x)k

. (14.2.1)

The rate of increase in births between y and x years ago is estimated as

y − x

log



B(t − x)

B(t − y)



y − x

log



∗



= r

y − x

log l

−(y−x)k

= r

− k log l

(14.2.2)

We could have taken our standard µ(a) to apply to the cohort midway

between that aged x and that aged y at the time of the census and obtained

approximately the symmetrical expression

≈ r

− k log



. (14.2.3)

14.2. Proportional Change in Mortality 339

[Prove this.] Both (14.2.2) and (14.2.3) show that a negative k for declining

mortality, along with log l

or log



, which are always negative, gives

a subtraction from the r calculated from (14.1.1); under the conditions of

declining mortality (14.1.1) suﬀers from an upward bias in estimating the

rate of increase of births.

But once again the historic rate of increase of births is not what we need

most. We want change in population, and the survivorship will more than

oﬀset the correction in (14.2.3). First we review what we know from Section

4.3 of the eﬀect on

of a proportional change in mortality.

Change of

. The ratio of expectations of life for populations of diﬀer-

ent periods or cohorts with l(a) changing by ﬁxed fractions will depart

substantially from unity, but never by as much as the ratio of age-speciﬁc

mortality (Section 4.3). If one of two populations has mortality µ(a)and

the other µ

∗

(a)=µ(a)(1 + k), the ratio of the expectation of life of the

second to the ﬁrst is

∗



l(a)

1+k



l(a) da

and, on expanding around k = 0 to the ﬁrst term of a Taylor series, this

becomes

∗

≈





l(a)+kl



(a)





l(a) da

, (14.2.4)

where l



(a) is the derivative of l(a)

1+k

with respect to k evaluated at k =0.

Now dl(a)

1+k

/dk =logl(a)l(a)

1+k

= l(a)logl(a)atk =0.Thenwehave

to the linear approximation

∗

=1+k



l(a) log[l(a)] da



l(a) da

=1− kH,

(14.2.5)

where the quantity H, deﬁned in Section 4.3, is minus the average log l(a)

weighted by l(a). The parameter H of the life table is shown in Table 4.3 as

about 0.20 for contemporary male populations and about 0.16 for females,

these values being substantially lower than those for a generation earlier.

We will apply (14.2.5) with (y − x)k in place of k, since our assumption is

that mortality increases by k per year.

Increase in Total C ohort Population. To approach the rate of increase in

population rather than in births, we again calculate two cohorts, and com-

340 14. Some Types of Instability

pare the number of person-years lived in the cohort born at time t −y with

the number for that born at time t − x.

For the number of person-years in the cohort we multiply the births

by the expectation of life, as was done for r

to obtain (14.1.4), and the

outcome reduces to

= r

− k log l

y − x

log



∗



, (14.2.6)

on entering the values of (14.2.2). [Prove this.] On applying (14.2.5) with

(y − x)k in place of k, we obtain

= r

− k log l

y − x

log



1 − (y − x)kH



. (14.2.7)

Approximating with log(1 − α) ≈−α, this becomes ﬁnally

= r

− k(log l

+ H). (14.2.8)

Similarly to the case in which we assumed a constant absolute change in

mortality rates, this will apply a positive correction to r

when the death

rate is falling (k<0), whenever x is a young age.

Increase of Persons of Arbitrary Age. For arbitrary z, whether or not x<

z<y, we can ﬁnd the overall rate of increase by comparing the number of

individuals in the cohort aged y at time t with those in the cohort aged x

at time t. The ratio of the latter to the former is equated to e

(y−x)

,where

is the rate of increase sought. Thus we have the equation in r

, the rate

of increase of persons aged z,

(y−x)

)

1+k(y−x)

)

and the solution in r

= r

+ k log





, (14.2.9)

for the average increase during time t −y + z to t −x + z. [Use (14.2.9) to

provide an alternative derivation of (14.2.8).]

The correction to r

is negative for z<xand positive for z>x.The

general form (14.2.9) would be a good starting point for deriving the pre-

vious expressions of this section as well as others that will occur to the

reader. For x =0,k = −0.01, and r

=0.03 this gives the rate of increase

at four ages, with Mexican male mortality of 1966 as the base:

z =0 r

=0.0300

20 0.0314

40 0.0323

60 0.0347

The steady rise in the inferred rate of increase with age is clearly exhibited.

14.3. Changing Birth Rates 341

Demeny (1965) comes a step closer to realism by showing the eﬀect of a

decline of mortality (a one-year gain in

per calendar year) that continues

over a limited time (5 years, 10 years,..., 40 years). Unfortunately this

eﬀect cannot be expressed analytically.

14.3 Changing Birth Rates

The eﬀect of changing birth rates on the population rate of increase and

on its age distribution is easily determined to a good approximation if the

changes are the same for all maternal ages. The following is a generalization

of stable theory that permits drawing conclusions as to rates of increase

in a population, given its age distribution. In symbols, suppose that the

birth rate for women aged a at time t is m(a, t)=m(a)f(t) (Coale, 1963,

p. 8; Coale and Zelnik, 1963, p. 83). The argument that follows shows how

to infer the rates of birth and natural increase with some relaxation of the

restriction on (5.2.4), though not without specializing f(t).

The homogeneous form of the renewal equation (7.5.1) becomes

B(t)=



B(t − a)l(a)m(a)f(t) da.

In the birth function B(t − a) under the integral sign, express both time

t and age a as departures from A, the mean age of childbearing, so that

B(t −a) becomes B[(t −A) −(a −A)], and then expand the birth function

as a Taylor series around t − A:

B(t)=



B [(t − A) − (a − A)] l(a)m(a)f(t) da





B(t − A) − (a − A)B



(t − A)

(a − A)



(t − A) −···



l(a)m(a)f (t) da.

Dividing by R



l(a)m(a) da and carrying through the integration

expresses the right-hand side in terms of moments about A, the mean age

of childbearing. The ﬁrst moment is zero, and the second σ

,thevariance

of ages of childbearing. Dividing by B(t −A), taking logarithms, and then

expanding the logarithm of the series of moments, gives, up to second

log B(t) − log B(t − A)=logR

+logf (t)+



(t − A)σ

2B(t − A)

. (14.3.1)

Since the term involving the second derivative is only about 2 or 3 per-

cent of the value of the main term, it may be neglected in what follows.

This amounts to the outrageous assumption that all children are born at

342 14. Some Types of Instability

the same age of mother. No argument could show that this assumption

is reasonable, but numerical tests demonstrate that it makes little nu-

merical diﬀerence in this particular application. If the assumption seems

objectionable, however, the solution below could be regarded as a ﬁrst ap-

proximation, B



(t − A) calculated and entered in (14.3.1), and a more

exact result obtained. (Alternatively, the second derivative could be re-

placed by a second diﬀerence.) Adding both sides over every Ath value and

canceling leaves a summation of log f(t)atintervalsofA, the mean age of

childbearing:

log B(t)=logB

log R



log f(t),

and taking exponentials and writing e

for R

t/A

, approximately true when

the unit of time is very nearly a generation, gives

B(t)=B

exp{log f(0) + log f(A)+···

+logf[(n − 1)A]}.

(14.3.2)

After the particular function f(t)=exp[k

t + k

t(t −A)] is entered, the

summation is evaluated to t = nA as

B(t)=B

exp



rt + k

t(t + A)

+ k

t(t

− A

)



. (14.3.3)

The intended application being to an age distribution with typical age a,

we are interested in births at time −a, and these are obtained by putting

t = −a, in (14.3.3) and then dividing by the current population N:

B(−a)

= b exp



−ra +

a(a − A)

−

− A



, (14.3.4)

where b is the current birth rate. Once an age distribution c(a)isgivenfor

a population that can be assumed to be closed and whose life table is l(a),

B(−a)/N can be estimated by c(a)/l(a). Taking logarithms and ﬁtting to

at least four ages produces the four constants b, r, k

,andk

.Amore

detailed derivation of (14.3.4) and the ﬁtting to data are given in Keyﬁtz

et al. (1967).

If k

= k

= 0, (14.3.4) reduces to an equation of Bourgeois-Pichat

(1958), shown in Section 5.5. In the more general case where only k

=0,

we have the result due to Coale and Zelnik (1963, p. 83).

Fitting (14.3.4) to an age distribution, when we are given or may assume

a life table, estimates not only the rate of increase and the birth rate but

also the change in the latter as indicated by k

and k

. Based on four

or more ages, the four constants b, r, k

,andk

are obtained, and these

permit a reconstruction of the age distribution by multiplying the right-

hand side of (14.3.4) by l(a). The age distribution so obtained can be

compared with the observed age distribution. The ﬁt may be compared with

14.4. Announced Period Birth Rate Too High 343

Table 14.1. Estimates of birth rates and other parameters from (9.3.4) for ﬁve

populations, ﬁtted to ages 5 to 74

Country and year 1000b 1000r 1000k

1000k

Fiji Islands, 1964 38.7 31.9 −6.0 0

France, 1899–1903 19.3 −4.6 −23.5 −0.3

Honduras, 1965 42.9 34.4 −5.6 0

Japan, 1962 16.8 −3.5 −51.6 −0.5

Netherlands, 1901 31.8 14.7 −12.1 −0.2

that resulting when k

is put equal to zero, and when k

= k

= 0. Unless it

is substantially better, one would avoid the complication of the additional

constants; but if the reconstruction of ages is markedly improved with the

nonstable method here described, so presumably also are the estimates of

b and r.

Table 14.1 gives estimates for certain countries of the four constants

contained in (14.3.4). The usefulness of these is suggested by the fact that

in all ﬁve cases the model reproduces their age distribution at ages 5 to

74 appreciably better than does the stable model with k

= k

=0.In

two instances the k

did not appreciably improve the ﬁt; in the other three

it did, but the calculated k

was small. Note that k

always turned out

negative, reﬂecting falling birth rates.

14.4 Announced Period Birth Rate Too High

When successive cohorts bear children at younger and younger ages, each

period cross section will tend to catch more births than any cohort. The

period births are “too many” in the sense that no one cohort of women

has so high an average; the childbearing of successive cohorts overlaps in

each period. In the early 1940s there were many marriages and hence ﬁrst

births, and Whelpton (1946) showed from the 1942 registrations that if the

pace continued women would average 1.084 ﬁrst births each. Conversely,

when couples are having their children later and later, a given period will

catch less than its share of births, that is to say, fewer than pertain to any

cohort.

To prove this and similar propositions requires a formal means of trans-

lating cohort moments into period moments and vice versa. The problem

in its general form has been solved by Ryder (1964). What follows is a

self-contained adaptation of his solution.

If the same life table applies at all times, and the probability at time t of

a woman of age x to x+dx having a child is m(x, t) dx, the net reproduction

344 14. Some Types of Instability

rate R



l(x)m(x, t) dx,

where α and β are the youngest and oldest ages, respectively, of childbear-

ing, and l(x) is the chance that a child just born will live at least to age x.

The R

is a function of time; the fact that fertility varies with time as well

as with age is what gives rise to our problem.

The nth period moment at time zero about age A chosen arbitrarily is

deﬁned as

(A)



(x − A)

l(x)m(x, 0) dx



l(x)m(x, 0) dx

where the R

does not depend on A.Thenth cohort moment is similarly

∗

(A)

∗

(A)



(x − A)

l(x)m(x, x − A) dx



l(x)m(x, x − A) dx

in which R

∗

(A) does depend on A. The cohort moment contains a time

argument x −A, contrived so that m(x, x −A) follows the group of women

born A years before time t down their life lines. It selects out of the period

births as oﬃcially published for successive years those appropriate to the

particular cohort (Figure 14.2).

The cohort R

∗

(A) is expressible in terms of R

(A), R

n+1

(A),..., by

means of a Taylor expansion of m(x, x − A)abouttimet = 0. For this

expansion m(x, x − A) is treated for any ﬁxed age x as a simple function

of time, so that for each x,

m(x, x −A)=m(x, 0) + (x −A)˙m(x, 0) +

(x − A)

¨m(x, 0) + ···, (14.4.1)

the dots representing diﬀerential with respect to time. The accuracy of

approximation by a given number of terms will depend on the smoothness

of whatever changes are taking place in the birth function.

Entering the Taylor expansion (14.4.1) in the expression for R

∗

(A)gives

∗

(A)



(x − A)

l(x)[m(x, 0) + (x − A)˙m(x, 0) + ···] dx. (14.4.2)

To put this into convenient form we have to convince ourselves that the

integral



(x − A)

n+1

l(x)˙m(x, 0) dx is the derivative with respect to time

of the period moment, that is, equals

n+1

(A), and similarly for later

terms. The proof consists in representing ˙m(x, 0) as a diﬀerence between

two values, m(x, ∆) and m(x, 0), divided by ∆. Before letting ∆ tend to