Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

14.4. Announced Period Birth Rate Too High 345

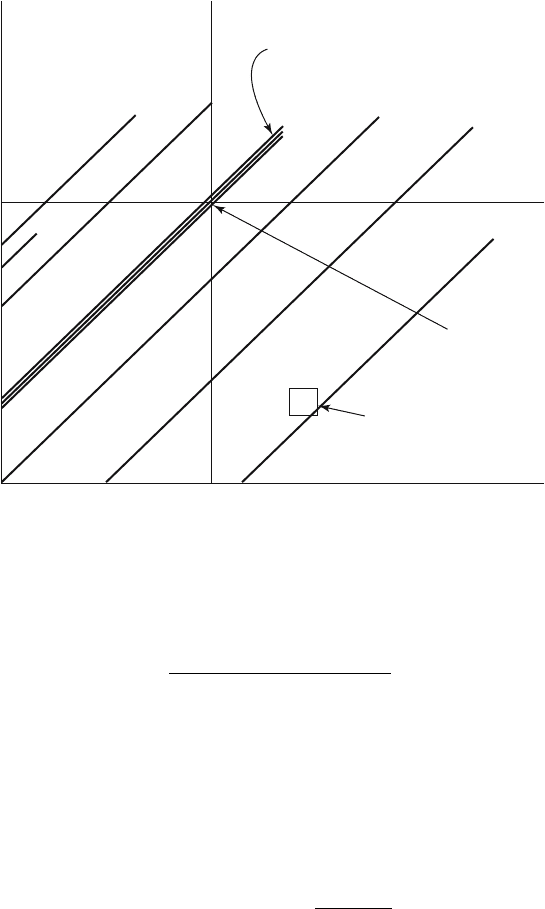
t Time

–A

a Age

(A, 0)

Strip for cohort born

at time –A.

Fertility is m(a, a – A)

Density

m(a, t) dadt

Figure 14.2. Cohort and period fertility.

zero, note that the integral



(x − A)

n+1

l(x)m(x, ∆) dx is R

n+1

(A)at

time ∆, say R

n+1

(A, ∆), and similarly when ∆ is replaced by zero. The

diﬀerence of the two integrals divided by ∆ is

n+1

(A, ∆) − R

n+1

(A, 0)

∆

and this becomes

n+1

(A, 0) =

n+1

(A) as ∆ tends to zero. A similar

proof would show that later terms of (14.4.2) become

n+2

(A)/2, and so

on. Expressed more brieﬂy, the fact we are using is that the integral of a

derivative equals the derivative of an integral under conditions far more

general than are required for the demographic application.

On incorporating this fact, expansion 14.4.2 leads to the fundamental

result

∗

(A)=R

(A)+

n+1

(A)+

n+2

(A)

+ ···, (14.4.3)

which estimates the nth cohort moment in terms of the nth and higher

period moments (Ryder, 1964). The most interesting application of (14.4.3)

will be for n = 0, and, truncating the series at the second term on the right,

346 14. Some Types of Instability

we obtain

∗

(A) ≈ R

(A)

≈ R



(A)



(14.4.4)

the zeroth period moment not depending on the arbitrary A.Inwords,we

can say that the cohort net reproduction rate is equal to the period net

reproduction rate plus the change over unit time in R

(A).

The theoretical result 14.4.4 can be illustrated arithmetically. To do so,

the net maternity function for United States females in 1967 was graduated

by a Hadwiger function (Keyﬁtz, 1968, p. 149); then, leaving R

and the

variance σ

the same in all periods as in 1967, the mean µ was shifted

upward by 0.1 year per 5-year period. This produces the results shown in

Table 14.2 for 1972 to 2012. It is seen that the period net reproduction

rate remains always at 1.205. A change in the mean of 0.1 year per 5 years

is a change at the rate of 0.02 per year. The right-hand side of (14.4.4) is

therefore 1.205(1 + 0.02) = 1.229.

If we add the diagonals for the three completed cohorts in Table 14.2,

we ﬁnd R

∗

=1.230, diﬀerent from the 1.229 of (14.4.4) by rounding error

only.

A virtually identical argument expresses the period R

(A)intermsof

the series of cohort moments R

∗

(A), R

∗

n+1

(A),...:

(A)=R

∗

(A) −

∗

n+1

(A)+

∗

n+2

(A)

−···, (14.4.5)

the diﬀerence from (14.4.3) being that the signs on the right-hand side here

come out alternately positive and negative.

Note that (14.4.3) and (14.4.5) serve quite diﬀerent purposes. The ﬁrst is

useful because it can incorporate the latest period information to suggest

how current cohorts are likely to be completed, on which deﬁnitive statis-

tics await their members reaching age 50 or so if they are women, older

if they are men. Equation (14.4.5), on the other hand, shows how the co-

horts, considered as the basic units underlying the process, are translated

or distorted in the course of expressing themselves in successive periods.

Among other uses such results provide information on the relative varia-

tion through time of cohort and period fertility. If it were true historically

that when R

rises R

(A) tends to fall, that is,

(A) is negative, and when

falls R

(A) tends to rise, then the variation of R

∗

(A)=R

(A)

would be smaller than the variation of R

by itself. Changes in the pe-

riod net reproduction rate being in these circumstances oﬀset by contrary

changes in the mean age of childbearing, and the cohort R

∗

being subject

to less variation than the period R

, R

∗

is useful in predicting future popu-

lation, since all prediction depends on ﬁnding functions that are relatively

constant. (Section 12.4)

14.4. Announced Period Birth Rate Too High 347

Table 14.2. Net maternity function for United States females, 1967, as graduated

by Hadwiger function; later periods supposing increase of 0.1 in mean age µ of

each successive period, with total R

and variance σ

ﬁxed at those of 1967

Year 10–14 15–19 20–24 25–29 30–34 35–39 40–44 45–49 Total

1967 0.0095 0.1512 0.3876 0.3656 0.1926 0.0710 0.0208 0.0066 1.205

1972 0.0088 0.1462 0.3846 0.3685 0.1960 0.0727 0.0213 0.0068 1.205

1977 0.0082 0.1413 0.3814 0.3714 0.1995 0.0744 0.0219 0.0071 1.205

1982 0.0076 0.1365 0.3781 0.3742 0.2030 0.0761 0.0224 0.0073 1.205

1987 0.0070 0.1318 0.3746 0.3769 0.2065 0.0778 0.0230 0.0074 1.205

1992 0.0065 0.1271 0.3711 0.3795 0.2100 0.0796 0.0236 0.0076 1.205

1997 0.0060 0.1226 0.3674 0.3821 0.2136 0.0814 0.0242 0.0079 1.205

2002 0.0055 0.1182 0.3636 0.3845 0.2171 0.0833 0.0248 0.0080 1.205

2007 0.0051 0.1138 0.3597 0.3869 0.2207 0.0851 0.0255 0.0082 1.205

2012 0.0047 0.1095 0.3557 0.3891 0.2244 0.0871 0.0261 0.0085 1.205

Note that all totals on rows are 1.205, the period R

; totals on the three complete cohorts

shown are R

∗

=1.230. The purpose of this hypothetical table is to show that the cohort

NRR can be constant and diﬀerent from the period NRR if the timing of fertility undergoes

a steady change.

If we knew that every cohort was aiming at exactly three children,

(14.4.3) and (14.4.5) would not be needed; we would simply deduct the

average number of children already recorded from three, and suppose the

remainder to be distributed over time and age in the future in some suit-

able way. If, on the other hand, cohorts had nothing to do with the matter,

we would treat the births to women of given age in successive periods as

an ordinary series and extrapolate. The theory of this section is especially

useful for the intermediate case in which the R

∗

for cohorts are shifting,

but less rapidly than the R

for periods.

We could have gone through the argument with gross reproduction rates

and obtained the same results, simply by omitting the l(x) throughout.

Even more generally, the m(a, t) function and the R’s representing the mo-

ments of m(a, t) could be interpreted, not as childbearing, but as mortality,

marriage, school attendance, income, or some other attribute of individ-

uals. The foregoing relation of periods and cohorts applies to any such

characteristic.

348 14. Some Types of Instability

14.5 Backward Population Projection

One may need to project a population backward, for instance to estimate

age distribution of a period before the ﬁrst of a series of censuses. Under

stability all ages increase in the same ratio; therefore one can calculate

the number living at the earlier period by dividing by this ratio. With or

without stability one can simply divide the total for an age group by the

probability of surviving to obtain the age group one time period earlier.

This gives the best possible answer in practice for all ages but the last,

to which it is inapplicable. The Leslie matrix is useless for such purposes,

being singular for any population that lives beyond its reproductive span;

it is of rank n − 1, where n is the number of age groups recognized.

An easy way to retrieve the last age interval is to suppose that it has been

increasing at the intrinsic rate of the population. But in some circumstances

one can do better than this by using the generalized inverse, which does

not require the assumption of stability (Greville and Keyﬁtz 1974).

First we express the projection backward along cohort lines in matrix

form as

⎛

⎜

⎝

00··· 0

0 ··· 0

00 0

··· 0

00 0 0 ···

5n−10

5n−5

00 0 0 ··· 0

⎞

⎟

⎠

which premultiplies the vector (say of females) at time t to provide an

estimate for time t −1 of all age intervals except the last, say 85 and over.

This contains the main elements of the required backward projection, and

is therefore at least a commonsense inverse of the forward projection A

(Section 3.1).

There are many generalized inverses of a given singular matrix, and the

choice of one from among them depends on the use to be made of it. If A is

the given matrix, it is usual to choose a generalized inverse X that satisﬁes

at least one and preferably both of the two relations (Rao and Mitra 1971)

AXA = A (14.5.1)

and

XAX = X; (14.5.2)

14.5. Backward Population Projection 349

the ﬁrst says that the backward form X must be such that projecting

forward, then backward, and then forward again is equal to projecting

once forward, and an equally obvious interpretation applies to the second.

In fact X

is a reasonably satisfactory generalized inverse of A.LikeA,

it is of order n and rank n − 1. One can easily verify that it satisﬁes both

(14.5.1) and (14.5.2). A disadvantage of X

, however, lies in the fact that

by its use the population in the oldest age interval at t − 1alwayscomes

out zero.

This is easily remedied by observing that properties (14.5.1) and (14.5.2)

are retained if the zeros in the bottom row of X

, except the ﬁrst, are

replaced by arbitrary elements. The last-row elements estimate the number

in the ﬁnal age interval at time t as some linear combination of the numbers

at time t +∆t in all age intervals except the youngest.

Of the many ways of arriving at such a linear estimate the most direct is

to use the eigenvalues and eigenvectors of the two matrices. For the classical

inverse of a nonsingular matrix H,if

Hx = λx,

then

−1

x = λ

−1

In words, we can say that a nonsingular matrix and its inverse have identical

eigenvectors, associated with respective eigenvalues that are reciprocals of

each other. It has been shown (Greville 1968) that something of the same

kind is true of a singular matrix and its generalized inverse.

The three important eigenvalues of the matrix are the real root, say λ

and the conjugate pair of complex eigenvalues closest to the real root in

absolute value, denoted as λ

and

. The real root is the ultimate ratio of

increase in the population that would result if the mortality and natality

conditions reﬂected in the Leslie matrix were perpetuated, while the pair

of complex roots is related to the amplitude and period of the oscillations

that would precede the attainment of a stable state.

The real cubic polynomial with leading coeﬃcient unity whose three zeros

are the reciprocals of these three eigenvalues is (λ

> 0),

q(z)=

z − λ

−1

z − λ

−1

z −

−1

= z

+ c

z + c

. (14.5.3)

To form a polynomial whose roots are the reciprocals of those of a given

polynomial all we need do is reverse the order of the coeﬃcients. [Show

that the roots of

+ c

n−1

+ ···+ c

are the reciprocals of the roots of

+ c

n−1

+ ···+ c

=0.

350 14. Some Types of Instability

Then, if λ

is the real root, and λ

= a + ib and

= a − ib are the main

complex roots, the characteristic equation with these roots is

(z − λ

)(z − λ

)(z −

)=0,

− (λ

+ λ

+(λ

+ λ

−λ

=0,

− (λ

+2a)z

+(2λ

a + a

+ b

)z − λ

+ b

)=0,

and the equation with the reciprocals of these roots is the same with

coeﬃcients reversed:

+ b

− (2λ

a + a

+ b

+(λ

+2a)z − 1=0.

Hence the coeﬃcients of (14.5.3) are

= −

2λ

a + a

+ b

)

+2a

+ b

)

= −

+ b

)

Let p

denote the survival rate from the ith age interval to the (i + 1)th

(which is the ith subdiagonal element of A). Then, if we take X

to be a

matrix like X

except that the last three elements of the bottom row are

−c

n−1

n−2

, −c

n−1

, −c

(14.5.4)

(instead of zeros), it is easily veriﬁed that the characteristic polynomial of

is z

n−3

q(z). Thus the eigenvalues of X

consist of n − 3 zeros and the

reciprocals of λ

, λ

,andλ

. It is possible to show that A and X

have in

common the eigenvectors associated with these three eigenvalues.

The rule seems to be that for long-term projection backward one cannot

improve on the dominant root to estimate the oldest age group. For back-

ward projection over a short interval, however, the ﬁrst three roots often

seem to help. In general, the shorter the interval over which one projects

backward the more possible it is to preserve minor roots without ﬁnding

erratically large and impossibly negative populations.

14.5.1 Application

Let us test these suggestions by backward projection of the older United

States female population from 1967: using data from that year only, we will

estimate for 1962. For all age intervals but the last this will of course be

done by the reciprocal of the survival ratio, a procedure whose properties

are straightforward and well known.

From the vital statistics for 1967 the real root is λ

=1.0376, and the

roots following are λ

=0.3098 ± 0.7374i. The polynomial q(z)of

14.5. Backward Population Projection 351

(14.5.3) is

q(z)=z

− z

(1.9323) + z(2.4966) − 1.5065.

The probability of survival into the last age interval is p

n−1

=0.8024, and

into the second-to-last interval is p

n−2

=0.7030. Hence the bottom row of

the inverse matrix ends up with the three numbers



..............................

... 0.8498 −2.0032 1.9323



and they are to premultiply the last three intervals (75 to 79, 80 to 84,

85+) of the 1967 age distribution:

⎛

⎜

⎝

···

2198

1286

727

⎞

⎟

⎠

expressed in thousands. The inner product of the two triplets of numbers

above constitutes the estimate in this particular way of forming the inverse,

and it turns out to be 696 thousands. The observed 1962 ﬁgure was 602

thousands. With the procedure of projecting backward by the reciprocal of

the real root alone we obtain 727/1.0376 = 701, which is a slightly larger

discrepancy.

For some other populations, the superiority of the three roots method

shows more clearly. For example, using data for Belgium, 1960, to estimate

women aged 85 and over for 1955, we ﬁnd that the three roots method gives

31,323 and one root gives 33,543 against an observed 1955 ﬁgure of 27,880.

Bulgaria, 1965, projects backward to 1960 on three roots at 17,550, and

on one root at 23,567, against an observed 15,995. In terms of percentage

error, the three cases show the following results:

Data Three Roots One Root

United States, 1967 15.6 16.4

Belgium, 1960 12.3 20.3

Bulgaria, 1965 9.7 47.3

The idea of using the generalized inverse occurred to Thomas Greville

as a way of formalizing and extending the projection backward along co-

hort lines, sometimes called reverse survival, that is used by demographers.

This method contrasts with projecting backward by truncating the Leslie

matrix at the last age of reproduction and then using its ordinary inverse.

Numerical experiments show no circumstance in which such a method is

comparable in accuracy with reverse survival; working back from an ob-

served age distribution gives large negative numbers from the ﬁrst or second

5-year period onward. If one starts with the artiﬁcial age vector obtained by

projecting forward on the Leslie matrix, it is possible to project backward

352 14. Some Types of Instability

on the inverse of the truncated matrix for a few periods, but this serves no

purpose, except possibly to study the accuracy attained in double precision

by the particular computer in use. All these statements reﬂect the severely

ill-conditioned nature of the truncated matrix.

Attempts to project the population backward for long periods of time

run afoul of ergodicity. Any two initial age distributions subjected to the

same sequence of vital rates converge toward each other. Thus there are

many historical series of age structures that could have led to any present

structure, and an attempt to work backwards is doomed to failure. His-

torical demographers have had to confront this problem in attempts to

reconstruct demographic trends from limited data on population size and

births and deaths (Lee 1985, 1993).

14.6 The Time to Stability

A baby boom or other irregularity in the time curve of births tends to be

echoed in each later generation insofar as the subsequent age-speciﬁc rates

of birth and death are constant. The mechanism, expressed in words, is

that, when the girls born in a baby boom are of reproductive age, mostly

about 20 to 30 years later, there will be more mothers in proportion to the

population, and consequently again more children. Still in commonsense

terms, the narrower and less skewed the range of ages in which women

bear children, the more concentrated will be the echo, and the larger the

ratio to the original disturbance. With a broad range of ages of childbear-

ing, especially one skewed to older ages, the waves would seem likely to

disappear more quickly, again supposing ﬁxed subsequent rates.

Insofar as such ﬂuctuations incur social cost in ﬁrst overcrowded and then

underutilized facilities such as schools, one is interested in the quickness of

convergence to stable form of a population that has undergone a perturba-

tion. In recent decades the variance of ages of childbearing in the United

States has diminished. Does this mean a slower reversion to stability after

a disturbance? Or does skewness help more than variance to speed the con-

vergence to stability? One way of answering these questions is in terms of

the main complex roots of the Lotka equation. In the matrix model frame-

work, the corresponding analysis is in terms of the subdominant eigenvalue

of the projection matrix (Section 7.3.1).

The literature on time to convergence was initiated by Coale (1968,

1972), and contributions have been made by Sivamurthy (1971), Trussell

(1977), Tuljapurkar (1982, 1993), Schoen and Kim (1991) and others.

14.6. The Time to Stability 353

14.6.1 The Criterion of Convergence

Underlying and facilitating all this work is the fact that the real part of the

second largest root in absolute value, r

in (7.5.2), largely determines the

time to convergence. The magnitude of contribution of the term e

,which

canbewrittenase

(x+iy)t

, depends on e

. The ratio of the asymptotic eﬀect

of the second root to that of the ﬁrst, as these are projected to t years, is

(this is the inverse of the damping ratio deﬁned in Section 7.3.1;

suppose that we want to know when the ratio will be less than :

(x−r)t

<.

Remembering that x − r is negative, we have

log 

x − r

. (14.6.1)

Note that this studies convergence in terms of the exponentials in t of

(7.5.2) and takes the constants Q into .

14.6.2 Use of the Characteristic Equation

Start with equation 6.1.2,



−ra

l(a)m(a) da =1,

divide both sides by R

, the net reproduction rate, take logarithms, expand

the exponential, and so obtain the series of cumulants

µr − σ

+ µ

−···−log R

=0, (14.6.2)

which is Lotka’s equation 161 (1939, p. 69) and is the same as (6.2.1) if

ψ(r) is put equal to unity. Entering r = x + iy gives for the real part

φ = µx −

− y

)

− 3xy

)

−

− 6x

+ y

)

− 10x

+5xy

)

120

−···−log R

=0,

(14.6.3)

and for the imaginary part

θ = µy − σ

xy +

(3x

y − y

)

−

y − xy

)

(5x

y − 10x

+ y

)

120

−···=0.

(14.6.4)

The characteristic equation 6.1.2 is expressed as φ + iθ = 0. Designate

derivatives of the real and complex parts with respect to the second cumu-

354 14. Some Types of Instability

lants as φ

and θ

, respectively, with respect to the third cumulants as φ

and θ

, with respect to x as φ

and θ

, and with respect to y as φ

and θ

and similarly for x and y with respect to the cumulants. In this shorthand

∂x/∂σ

, for example, will be written as x

,and∂x/∂µ

as x

. Completely

diﬀerentiate the real part, φ =0,byσ

and µ

in turn:

+ φ

= 0 (14.6.5)

+ φ

=0, (14.6.6)

and the same for the imaginary part, θ =0:

+ θ

= 0 (14.6.7)

+ θ

=0. (14.6.8)

The ﬁrst and third of these equations in partial derivatives can be solved

for x

, the derivative of x with respect to variance:



−φ

−θ



where |X| is the determinant of X. The second and fourth equations can

be solved for x

, the derivative with respect to the third moment:



−φ

−θ



The denominators are the same for x

and x

, and we want the ratio



−φ

−θ



−φ

−θ



− θ

This simple expression provides the ratio of the eﬀect of σ

on x to

the eﬀect of µ

on x,sincex

is shorthand for (∂x/∂σ

)/(∂x/∂µ

It assumes that the second and third moments can vary independently of

each other, and that all other moments are ﬁxed, including R

, the net

reproduction rate.

14.6.3 Exact and Approximate Ratios of Partial Derivatives

To evaluate x

we refer back to the expansions of φ and θ and calculate

the partials:

= µ − σ

x +

− y

)

+ ···