Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

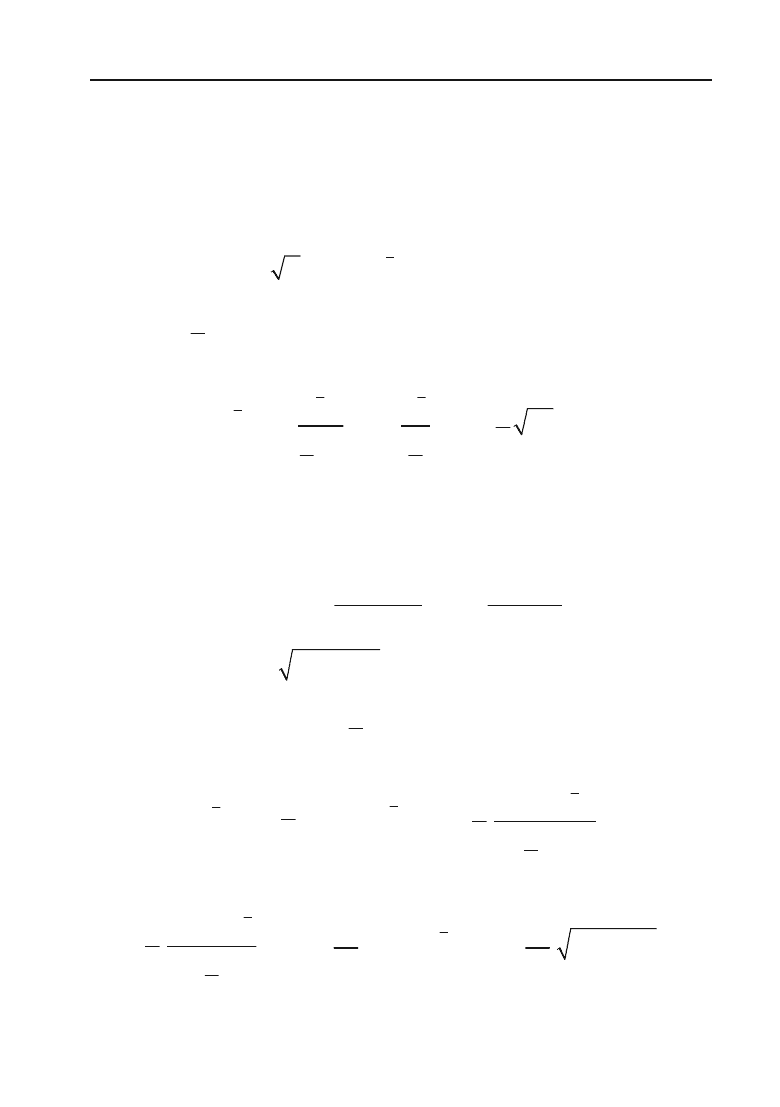
371
Розділ VI. Інтегральне числення
§ 6.2. Методи інтегрування
6.2.1. Метод безпосереднього інтегрування.
Розв’язання прикладів
Знайти інтеграли.
Приклад 6.1.
x
dx
³
=
1
2
x
dx
³
представляє формулу (1) при
v = x
,
n =
1
2
.
Згідно цієї формули маємо
1
2
x
dx
³
=
13
1
22
13
1
22
x
x
C
+ С =
3
2
3
x
+ С.
Приклад 6.2.
7
(5)
x
dx
³
представляє формулу (1) при
v = x +
5;
dv = dx
;
n =
7, згідно якої маємо:
7
(5)xdx
³
=
71
(5)
71
x
+ С =
8
(5)
8
x
+ С.
Приклад 6.3.
2
5
(3 4)
x
dx
³
представляє формулу (1) при
v =
(3
x –
4);
dv
=
3
dx
;
n =
2
5
, згідно якої маємо:
2
5
(3 4)
x
dx
³
=
1
3
2
5
(3 4) 3
x
dx
³
=
1
3
2
1
5
(3 4)
2
1
5
x
+ C =
=
1
3
7
5
(3 4)
7
5
x
+ C =
5
21
7
5
(3 4)x
+ C =
5
21
7
5
(3 4)x
+ C.

372
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 6.4.
2
36 5
xdx
x
³
представляє формулу (2)
при
v =
36
–
5
х
2
;
dv
=
2
(36 5 )
x
x
c
dx = –
10
x dx,
згідно якої маємо
2
36 5
xdx
x
³
=
1
10
2
10
36 5
xdx
x
³
=
1
10
ln
|
36
–
5
x
2
| + C.
Приклад 6.5.
2
36 5
dx
x
³
представляє формулу (10) при
v = x
5
;
dv =
5
dx, a =
6. Згідно цієї формули маємо:
2
36 5
dx
x
³
=
22
6(5)
dx
x
³
=
22
15
56 ( 5)
dx
x
³
=
=
11
6
5
arctg
5
6
x
+ C =
1
65
arctg
5
6
x
+ C.
Приклад 6.6.
2
536
dx
x
³
представляє формулу (11)
при
v = x
5
;
dv =
5
dx, a =
6. Згідно цієї формули маємо:
2
536
dx
x
³
=
1
5
22
5
(
5
)
6
dx
x
³
=
1
5
1
26
ln
56
56
x
x
+ C =
=
1
12 5
ln
56
56
x
x
+ C.
Приклад 6.7.
2
536
dx
x
³
представляє формулу (12) при
v =
6
x;
dv =
6
dx, a =
5
,
згідно цієї формули маємо:
2
536
dx
x
³
=
22
(5) (6)
dx
x
³
=
1
6
22
6
(5) (6)
dx
x
³
=
373
Розділ VI. Інтегральне числення
6.2.2. Інтегрування методом розкладу
Цей метод оснований на розкладі підінтегральної функції на суму
функцій, від кожної з яких первісну можна знайти за допомогою
табличних інтегралів.
6.2.2.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.9.
53
(2 2 7)
x
xdx
³
=
5
2
x
dx
³
–
3
(2
x
dx
³
+
7dx
³
=
=
15
2
x
dx
³
–
3
2
13
x
dx
³
+
7 dx
³
=
1
1
5
2
1
1
5
x
–
3
2
1
1
3
1
1
3
x
+
7
x + C =
=
6/5
2
6/5
x
–
3
2
4/3
4/3
x
+
7
x + C =
5
3
x
6/5
–
3
32
4
x
4/3
+
7
x + C =
=
5
3
6
5
x
–
3
32
4
4
3
x
+
7
x + C.
=
1
6
arcsin
6
5
x
+ C.
Приклад 6.8.
2
36 5
dx
x
³
представляє формулу (12) при
v =
6
x
;
dv =
6
dx, a =
5
,
згідно цієї формули маємо:
2
36 5
dx
x
³
=
22
(
6
)(
5
)
dx
x
³
=
1
6
22
(
6
)(
5
)
dx
x
³
=
=
1
6
ln
|
6
x +
2
36 5x
| + C.
374
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 6.10.
3
(2 1)xdx
xx
³
=
32
(
2
)
3
(
2
)
32 1xx x
xx
³
dx
=
=
3/2 1/2
3/2
81261xxx
x
³
dx
=
3/2 1/2
3/2 3/2 3/2 3/2
8126 1xxx
xxxx
§·
¨¸
©¹
³
dx
=
=
8 dx
³
+
12
12 xdx
³
+
1
6 xdx
³
+
32
xdx
³
=
8
x +
12
1
1
2
1
1
2
x
+
+ 6 ln
|x| +
3
1
2
3
1
2
x
+ C =
8
x +
24
x
+ 6 ln
|x| –
2
x
+ C.
Приклад 6.11.
2
()
xx
ee dx
³
=
22
(2 )
xxx x
eeeedx
³
=
2
x
edx
³
–
2 dx
³
+
+
2
x
edx
³
=
2
1
(
2
)
2
x
edx
³
–
2
x –
2
1
(2 )
2
x
edx
³
=
1
2
e
2x
–
2
x –
–
1
2
e
–2x
+ C.
Приклад 6.12.
2
3
5
x
dx
x
³
=
22
3
55
x
dx
xx
§·
¨¸
©¹
³
=
2
5
xdx
x
³
+
3
2
5
dx
x
³
=
=
2
12
2
5
xdx
x
³
+
3
22
() (
5
)
dx
x
³
=
1
2
ln
|x
2
–
5
| +
3
25
ln
5
5
x
x
+ C.
Приклад 6.13.
2
tg xdx
³
=
2
2
sin
cos
x
dx
x
³
=
2
2
1cos
cos
x
dx
x
³
=
2
22
1cos
cos cos
x
dx
xx
§·
¨¸
©¹
³
=
375
Розділ VI. Інтегральне числення
6.2.2.2. Приклади для самостійного розв’язання
Знайти інтеграли.
6.14.
37
dx
x
³
.
6.15.
2
(7 3 )
dx
x
³
.
6.16.
73
dx
x
³
.
6.17.
2
53
xdx
x
³
.
6.18.
2
37
dx
x
³
.
6.19.
2
57
dx
x
³
.
6.20.
2
53
dx
x
³
.
6.21.
2
95
dx
x
³
.
6.22.
2
47
dx
x
³
.
6.23.
23
(5 3 )
xdx
x
³
.
6.24.
2
74
dx
x
³
.
6.25.
5x
edx
³
.
6.26.
3
2
7
x
x
dx
³
.
6.27.
sin
x
dx
x
³
.
6.28.
2
3
3
23 5
x
x
dx
x
³
.
6.29.
23
4
xx
dx
x
³
.
6.30.
3
3
(1 )x
dx
x
³
.
6.31.
2
1
x
x
e
edx
x
§·
¨¸
©¹
³
.
=
2
cos
dx
x
³
–
dx
³
=
tg
2
x – x + C.
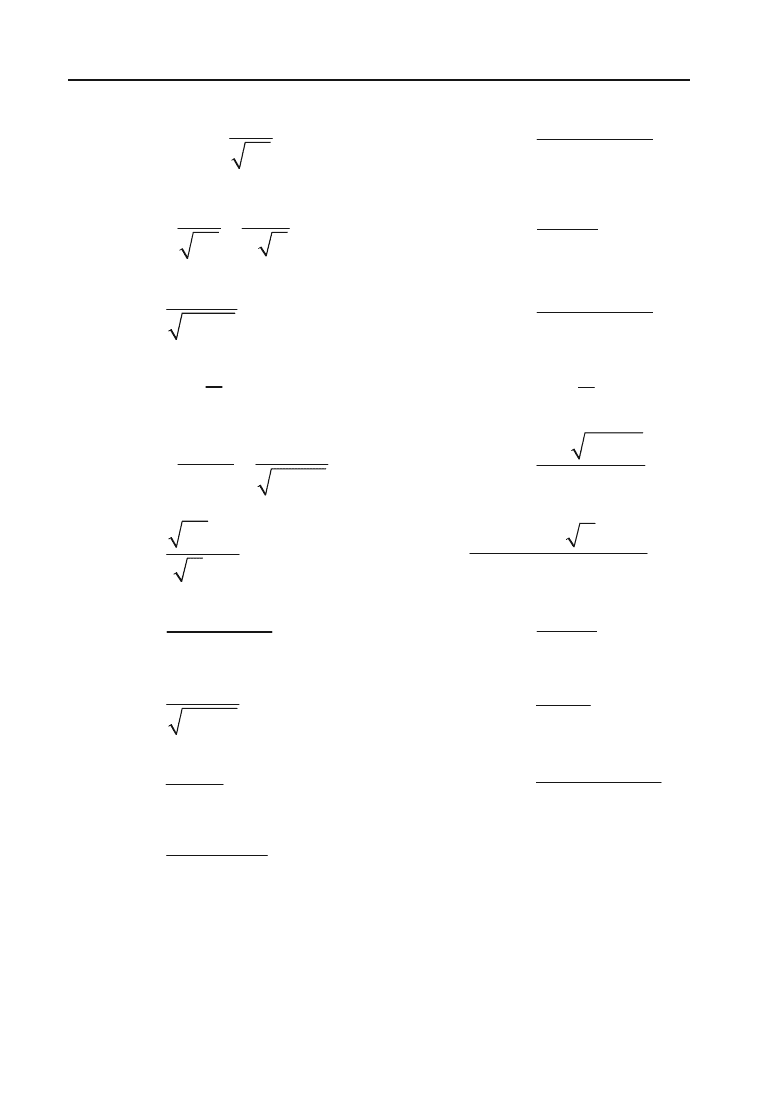
376
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.32.
3
1
x
x
a
adx
x
§·
¨¸
©¹
³
.
6.33.
22
cos2
cos sin
xdx
xx
³
.
6.34.
2
3
11
x
x
x
§·
¨¸
©¹
³
dx.
6.35.
2
34
4
x
dx
x
³
.
6.36.
2
1
1
x
x
³
dx
.
6.37.
22
cos sin
dx
xx
³
.
6.38.
2
sin
2
x
dx
³
.
6.39.
2
cos
3
x
dx
³
.
6.40.
2
2
23
1
1
dx
x
x
§·
¨¸
¨¸
©¹
³
.
6.41.
2
2
35
5
x
dx
x
³
.
6.42.
3
1
1
x
dx
x
³
.
6.43.
3
sin 2 cos
cos
x
xxx
dx
x
x
³
.
6.44.
2
56
3
xx
dx
x
³
.
6.45.
2
52
4
x
dx
x
³
.
6.46.
2
1
1
x
dx
x
³
.
6.47.
2
2
1
x
dx
x
³
.
6.48.
4
2
3
x
dx
x
³
.
6.49.
2
(3 2ln )
dx
x
x
³
.
6.50.
2
arctg 2
1
x
dx
x
³
.

377
Розділ VI. Інтегральне числення
6.2.3. Метод інтегрування частинами
Із формули диференціала добутку
d
(
u
v
) =
udv
+
vdu
інтегруван+
ням обох частин рівності одержується формула інтегрування части+
нами
udv uv vdu
³³
. (6.6)
За цією формулою знаходження інтеграла
udv
³
приводиться до
знаходження іншого інтеграла
vdu
³
. Застосовувати цю формулу
зручно в тих випадках, коли
udv
³
буде легко знаходитися. Для за+
стосування формули інтегрування частинами до інтегралу
()
f
xdx
³
необхідно підінтегральний вираз
f
(
x
)
dx
представити в вигляді добут+
ку двох співмножників
u
та
dv
. За
dv
завжди вибирають такий вираз,
що містить
dx
, із якого інтегруванням можна знайти
v
. За
u
в
більшості випадків приймається функція, яка при диференціюванні
спрощується.
6.2.3.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.51.
ln
x
dx
³
.
Розв’язок.
Нехай
ln ,
1
,
uxdvdx
du dx v dx x
x
³
За формулою інтегрування частинами маємо
ln xdx
³
= x
ln
x –
1
xdx
x
³
= x
ln
x –
dx
³
= x
ln
x – x + C.
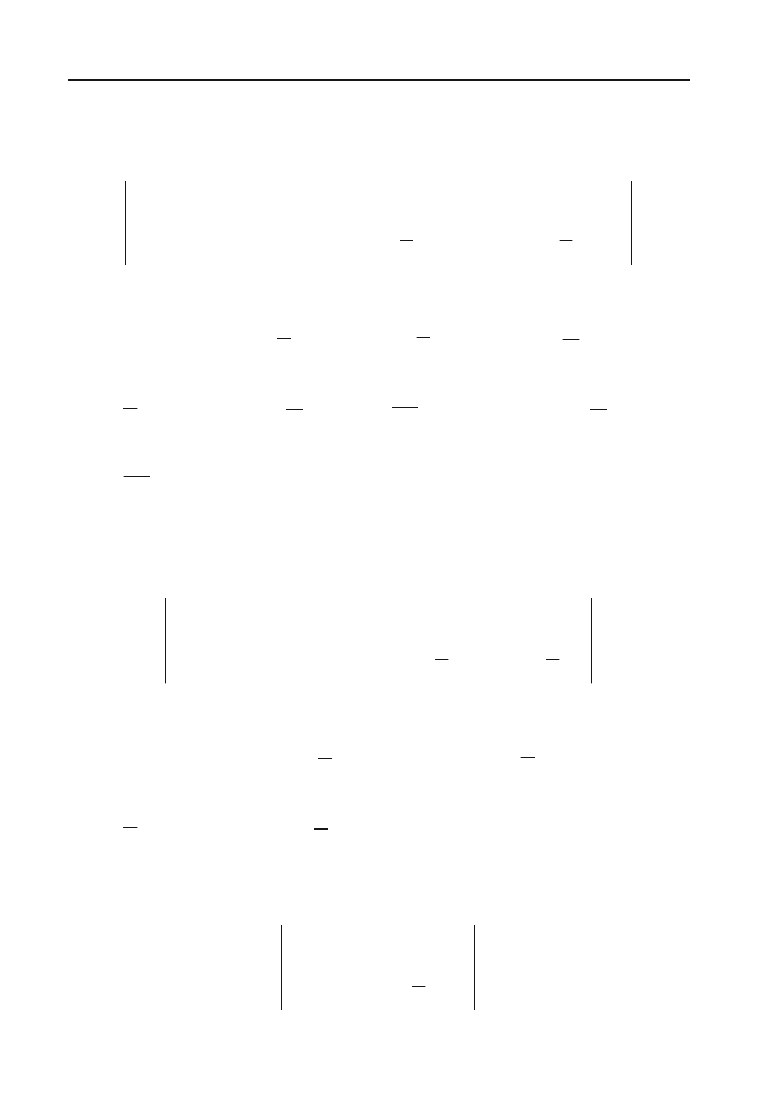
378
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 6.52.
sin5xxdx
³
.
Розв’язок.
Нехай
,
11
sin5 , sin5 sin5 5 cos5
55
u x du dx
dv xdx v xdx x dx x
³³
Використовуючи формулу, одержуємо
sin5
x
xdx
³
= x
(
1
5
cos
5
x
)
–
1
cos5
5
xdx
³
=
5
x
cos
5
x +
+
1
5
cos5xdx
³
=
5
x
cos 5
x +
1
25
cos5 5xdx
³
=
5
x
cos 5
x +
+
1
25
sin 5
x + C.
Приклад 6.53.
22
(35)
x
xxedx
³
.
Розв’язок.
Нехай
22
222
35,
11
(3 3) , 2
22
x
x
xx
ux x dvedx
du x dx v e dx e dx e
³³
Одержуємо
22
(35)
x
xxedx
³
=
1
2
e
2x
(
x
2
+
3
x –
5)
–
2
1
(2 3)
2
x
exdx
³
=
=
1
2
e
2x
(
x
2
+
3
x –
5)
–
1
2
2
(2 3)
x
xedx
³
.
До останнього інтеграла знову застосуємо формулу інтегрування
частинами.
2
2
23,
1
2,
2
x
x
ux dvedx
du dx v e
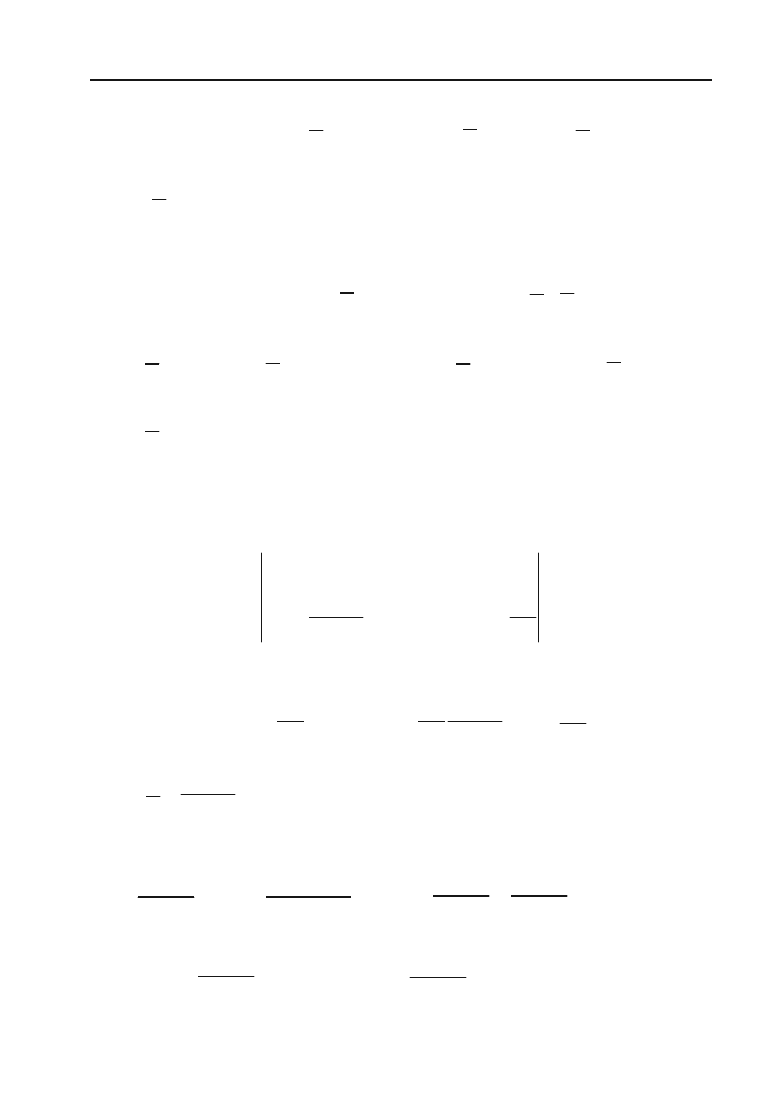
379
Розділ VI. Інтегральне числення
2
(2 3 )
x
xxedx
³
=
1
2
e
2x
(2
x +
3)
–
2
1
2
2
x
edx
³
=
1
2
e
2x
(2
x +
3)
–
–
1
2
e
2x
+ C.
Отже, одержуємо:
22
(35)
x
xxedx
³
=
1
2
e
2x
(
x
2
+
3
x –
5)
–
1
2
(
1
2
e
2x
(2
x +
3)
–
–
1
2
e
2x
+ C
)
=
1
2
e
2x
(
x
2
+
3
x –
5)
–
1
4
e
2x
(2
x +
3)
+
1
4
e
2x
+ C =
=
1
2
e
2x
(
x
2
+
2
x –
6)
+ C.
Приклад 6.54.
arctgxxdx
³
.
Розв’язок.
2
2
arctg ,
1
,
2
1
uxdvxdx
x
du dx v xdx
x
³
Одержуємо:
arctgxxdx
³
=
2
2
x
arctg
x –
2
2
1
2
1
x
dx
x
³
=
2
2
x
arctg
x –
–
1
2
2
2
1
x
x
³
dx.
Останній інтеграл знайдемо окремо:
2
2
1
x
dx
x
³
=
2
2
11
1
x
dx
x
³
=
2
22
11
11
x
dx
xx
§·
¨¸
©¹
³
=
=
2
1
1
1
dx
x
§·
¨¸
©¹
³
=
dx
³
–
2
1
1
dx
x
³
= x –
arctg
x + C.

380
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Звідки
arctgxxdx
³
=
2
2
x
arctg
x –
1
2
(
x –
arctg
x + C
)
=
2
2
x
arctg
x –
–
1
2
x +
1
2
arctg
x + C =
2
1
2
x
arctg
x –
2
x
+ C.
Приклад 6.55.
cos
ax
ebxdx
³
.
Розв’язок.
В цьому прикладі двократне застосування інтегруван+
ня частинами приведе до інтегралу, який мали за умовою.
cos
ax
ebxdx
³
=
,
1
cos , cos sin
ax ax
u e du e adx
dv bxdx v bxdx bx
b
³
=
=
1
b
e
ax
sin
bx –
1
sin
ax
bxe adx
b
³
=
1
b
e
ax
sin bx –
a
b
sin
ax
ebxdx
³
.
До останнього:
,
1
sin , sin cos
ax ax
ue dueadx
dv bxdx v bxdx bx
b
³
sin
ax
ebxdx
³
= –
1
b
cos
bx –
1
cos
ax
bxe adx
b
³
= –
1
b
cos
bx +
+
a
b
cos
ax
ebxdx
³
.
Повернемося до останньої умови. Позначимо одержаний інтег+
рал через
cos
ax
ebxdx
³
.
=
cos
ax
ebxdx
³
=
1
b
e
ax
sin
bx –
a
b
(
1
b
e
ax
cos
bx +
a
b
cos
ax
e bxdx
³
) =
=
1
b
e
ax
sin
bx +
2
a
b
e
ax
cos
bx –
2
2
a
b
cos
ax
ebxdx
³
.
