Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

351
Розділ V. Диференціальне числення функції багатьох змінних
z
x
w
w
M
= –
2,
z
y
w
w
M
=
–4,
grad
z
M
=
(–2; –4)
MN
=
grad
z
M
.
Задача 5.39.
z =
22
4
xy
,
точка
М
(–1; 2). Знайти ізокванту яка прохо+
дить через дану точку
М
і grad
1
2
x
y
z
.
Розв’язок.
z
x
w
w
=
222
4
()xy
2
х,
z
x
w
w
M
=
2
88
25
(1 4)
,
z
y
w
w
=
222
4
()xy
2
у
,
z
y
w
w
M
=
16
25
.
grad
z =
816
;
25 25
§·
¨¸
©¹
.
Рівняння ізокванти в загальному вигляді
22
4
()xy
= С
. Вибере+
мо
С
таким чином, щоб ізокванта проходила через точку
М
(–1; 2).
4
14
=
С
,
С
=
4
5
,
22
4
xy
=
4
5
,
тоді
х
2
+ у
2
=
5.
Ізоквантою буде коло з центром в точці (0; 0) і радіуса
5
.
–1 0 1 X
Y
2
1
–1
–2
M
N
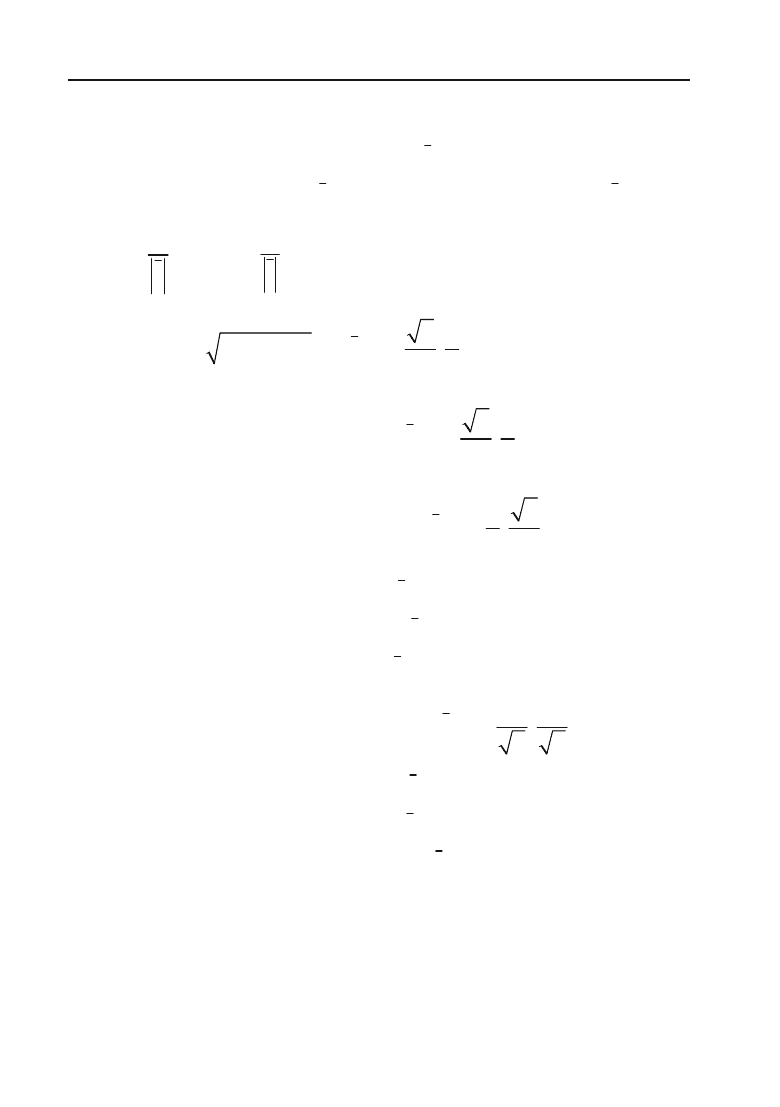
352
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
5.1.3. Задачі для самостійного розв’язання
Дано функцію
z = f
(
x
,
y
) напрямок
l
та точка
М
0
. Потрібно знай+
ти похідну за напрямком
l
в точці
М
0
та grad
z
. Якщо |
l
|
z
1, то
cos
D
=
x
l
l
, sin
D
=
y
l
l
.
5.40.
z =
ln
22
22
x
y
,
l
=
31
,
22
§·
¨¸
¨¸
©¹
, M
0
(1; –1).
5.41.
z =
2
x
2
–
3
y
2
,
M
0
(0; –2),
l
=
31
,
22
§·
¨¸
¨¸
©¹
.
5.42.
z = x
3
+ y
3
–
3
xy, M
0
(2; 1),
l
=
13
,
22
§·
¨¸
¨¸
©¹
.
5.43.
z =
3
x
2
–
2
xy, M
0
(0; 1),
l
=
(3; 4).
5.44.
z = x
3
– y
3
+ x
,
M
0
(1; 1),
l
=
(–1; 0).
5.45.
z =
2
x
3
–
3
y
2
,
M
0
(2; 0),
l
=
(0; 1).
5.46.
z =
2
xy +
6
x – y
,
M
0
(2; –1),
l
=
11
,
22
§·
¨¸
©¹
.
5.47.
z = x
2
y
3
–
3
x
2
y
,
M
0
(0; 1),
l
=
(2; 1).
5.48.
z =
5
x
4
–
4
y
3
,
M
0
(–1; 1),
l
=
(2; 0).
5.49.
z = –x
2
– xy
2
+
1,
M
0
(2; 3),
l
=
(0; –2).

353
Розділ V. Диференціальне числення функції багатьох змінних
§5.2. Екстремум функції двох змінних
Якщо функція
z = f
(
x
,
y
) має частинні похідні, то критичні точ+
ки, або точки підозрілі на екстремум, шукаються серед розв’язків
системи:
0
0
дz
дx
дz
дy
°
°
®
°
°
¯
Нехай
M
0
(
x
0
;
y
0
) — критична точка. Позначимо через
A
,
B
,
C
відпо+
відно значення:
2
2
дz
дx
,
2
дz
дxд
y
,
2
2
дz
дy
в точці
M
0
.
Якщо
1)
2
0AC B' !
, то функція досягає
max
z
(
x
0
;
y
0
) при
A
< 0,
min
z
(
x
0
;
y
0
)
при
A
> 0;
2)
2
0AC B'
, то екстремуму немає;
3)
2
0AC B'
— сумнівний випадок, потрібні додаткові дос+
лідження.
Важливими є задачі на умовний екстремум, коли шукається ек+
стремум функції
z = f
(
x
;
y
) при умові, що змінн
і x
та
y
зв’язані рівнян+
ням зв’язку
M
(
x
,
y
)
=
0.
Така задача зводиться до дослідження на безумовний екстремум
функції Лагранжа
(
,,
)
Lx
y
O
.
(
,
)(
,
)
L
f
x
y
x
y
OM
,
де число
O
називається
множником Лагранжа
.
Після виключення
O
досліджуємо на екстремум функцію Лаг+
ранжа, як функцію двох змінних
L
(
x
,
y
)
.

354
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
5.2.1. Розв’язання прикладів
Приклад 5.50.
Дослідити на екстремум функцію
22
9620zx xyy x y
.
Розв’язок.
Знаходимо частинні похідні функції
29
дz
xy
дx
,
26
дz
xy
дy
.
Розглянемо систему двох рівнянь з двома невідомими.
290
260
xy
xy
®
¯
Розв’язком цієї системи будуть числа
x =
– 4,
y
= 1. Точка
M
0
(–4; 1) називається
критичною
.
Знаходимо частинні похідні другого порядку в точці
M
0
.
0
2
2
2
M
дz
A
дx
,
0
2
2
2
M
дx
C
дy
,
0
2
1
M
дz
B
дxдy
,
2
413 0AC B' !
A
> 0, отже існує min функції в точці (–4; 1), min
z = z
(–4; 1) = –1
Приклад 5.51.
Дослідити на екстремум функцію двох змінних
2
6zyxy x y
.
Розв’язок.
Запишемо перші частинні похідні функції
1,
2
дz y
дx
x
26
дz
xy
дy
.
Розглянемо систему двох рівнянь з двома невідомими
355
Розділ V. Диференціальне числення функції багатьох змінних
10,
2
260
y
x
xy
°
®
°
¯
Розв’язком цієї системи є числа
x =
4,
y =
4
.
Знаходимо другі частинні похідні функції:
2
2
3
4
дz y
дx
x
,
2
2
2
дz
дy
,
2
1
2
дz
дxдy
x
.
Знайдемо значення других частинних похідних в точці (4, 4).
2
4
2
4
1
8
x
y
дz
A
дx
,
2
4
2
4
2
x
y
дz
C
дy
,
2
4
4
1
4
x
y
дz
B
дxдy
.
2
11 3
0,
41616
AC B' !
A
> 0, отже існує max функції
Z
,
max
= Z
(4; 4)
= 12.
Приклад 5.52
. Дослідити на екстремум функцію двох змінних
33
861
z
xyxy
.
Розв’язок.
Знаходимо перші частинні похідні функції
,
дz дz
дx д
y
.
2
36
дz
xy
дx
,
2
24 6
дz
y
x
дy
.
Запишемо систему двох рівнянь з двома невідомими
2
2
360
24 6 0
xy
yx
°
®
°
¯
Бачимо, що ця система має розв’язки
0
0
x
y
®
¯
та
1
1
2
x
y
°
®
°
¯

356
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Знаходимо другі частинні похідні функції.
2
2
6
дz
x
дx
,
2
2
48
дz
y
дy
,
2
6
дz
дxдy
.
Знаходимо значення других частинних похідних в точці (0; 0)
.
A
= 0,
C
= 0,
B
= –6,
2
0360AC B'
.
Перевіримо точку (1; 1/2).
A =
6,
C =
24,
B
= –6,
24 6 36 0' !
, A
> 0.
Існує min функції
z
min
= z
(1; 1/2) = 1 + 1 – 3 + 1 = 0.
Приклад 5.53
(На умовний екстремум). Знайти екстремум
функції
22
z
xy
при умові
10
xy
.
Функція Лагранжа буде мати вигляд
22
(,,) ( 1)Lxy xy xy
OO
.
Запишемо необхідні умови існування екстремуму:
20
дL
x
дx
O
,
20
дL
y
дy
O
,
10
дL
xy
д
O
.
Звідки отримуємо:
0
10
xy
xy
®
¯
та
1
2
1
2
x
y
°
°
®
°
°
¯
Критична точка буде мати координати:
(
12;12
)
M
,
1
O
.
22
(;) ( 1)Lxy x y x y
.
21
x
Lx
c
,
21
y
Ly
c
,
2
xx
LA
cc
,
2
yy
LC
cc
,

357
Розділ V. Диференціальне числення функції багатьох змінних
0
xy
LB
cc
,
тоді
2
40,AC B' !
0A !
,
отже існує min функції
min
(
1/2;1/2
)
1/4 1/4 1/2
z
z
.
5.2.2. Приклади для самостійної роботи.
Дослідити на екстремум функції двох змінних.
5.54.
22
800 40 60
z
xy x y
.
5.55
.
22
250 20 100
z
xy x y
.
5.56.
22
1800 80 60
z
xy x y
.
5.57.
22
2100 40 100
z
xy x y
.
5.58
.
22
1700 40 80
z
xy x y
.
5.59.
22
1500 20 80
z
xy x y
.
5.60.
22
2000 100 40
z
xy x y
.
Дослідити на умовний екстремум функції двох змінних.
5.61.
zxy
при
22
111
2
xy
.
5.62.
11
z
x
y
при
20
xy
.
5.63.
22
4zx y xyxy
при
30
xy
.
358
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§5.3. Метод найменших квадратів
Нехай залежність між двома змінними х та у задана у вигляді
таблиці, одержаної дослідним шляхом. Це можуть бути результати
досліду або спостережень, статистичні обробки матеріалу і інше.
Таблицю можна інтерпретувати як множину
n
точок на площині
хОу.
Треба підібрати функцію
y = f
(
x
), яка в певному розумінні «най+
кращим чином» була б вписана в множину даних точок. Якщо фун+
кція лінійна, тобто має вигляд
y = kx + b
, то використовуючи метод
дослідження на екстремум функції двох змінних (
k
,
b
),
одержимо
систему двох лінійних рівнянь відносно
k
i
b
:
2
111
11
nnn
iiii
iii
nn
ii
ii
x
kxbxy
xkbn y
§·§·
°
¨¸¨¸
°© ¹ © ¹
®
§·
°
¨¸
°
©¹
¯
¦¦¦
¦¦
Таку систему називають
системою нормальних рівнянь
.
х х
1
х
2
... х
і
... х
n
у у
1
у
2
... у
і
... y
n
5.3.1. Розв’язання прикладів
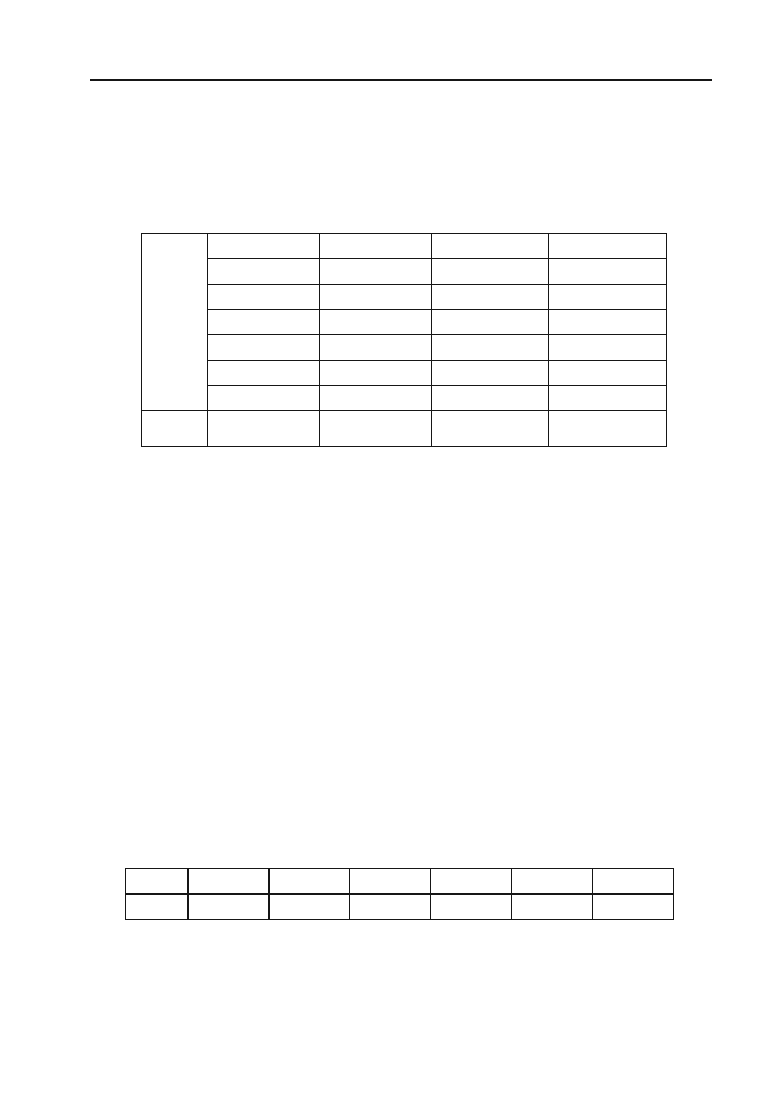
Задача 5.64.
Маємо дані про ціну на нафту
х
(гр. од.)
і індекс
акцій нафтових компаній
у
(ум. од.):
Припускаючи, що між змінними
х
і
у
існує лінійна залежність,
знайти емпіричну формулу виду
y = kx + b
, використовуючи метод
найменших квадратів.
х
17,28 17,05 18,30 18,80 19,20 18,50
у
537 524 550 555 560 552
359
Розділ V. Диференціальне числення функції багатьох змінних
Розв’язок.
Знайдемо необхідні для розрахунків суми
1
n
i
i
x
¦
,
1
n
i
i
y
¦
,
1
n
ii
i
x
y
¦
,
2
1
n
i
i
x
¦
, склавши допоміжну таблицю:
Система нормальних рівнянь має вигляд:
1988,52 109,13 59847,06
109,13 6 3288
kb
kb
®
¯
Розв’язавши систему, знайдемо
k =
12,078,
b =
328,28.
Тоді
y
= 12,078
x
+ 328,28.
Таким чином, із збільшення ціни нафти на 1 грошову одиницю
індекс акцій нафтових компаній в середньому зростає на 12, 078 ум. од.
х
і
у
і
х
і
у
і
х
і
2
17,28 527 9279,36 298,598
17,05 524 9104,70 290,702
18,30 550 10065,00 334,890
18,80 555 10434,00 353,440
19,20 560 10752,00 368,640
18,50 552 10212,00 342,250
¦
109,13 3288 59847,06 1988,520
5.3.2. Задачі для самостійного розв’язання
Задача 5.65.
Використовуючи метод найменших квадратів, знай+
ти емпіричну формулу
y = kx + b
для функції заданої таблицею:
х
0,5 1,0 1,5 2,0 2,5 3,0
у
0,7 1,7 1,6 3,1 3,6 4,6
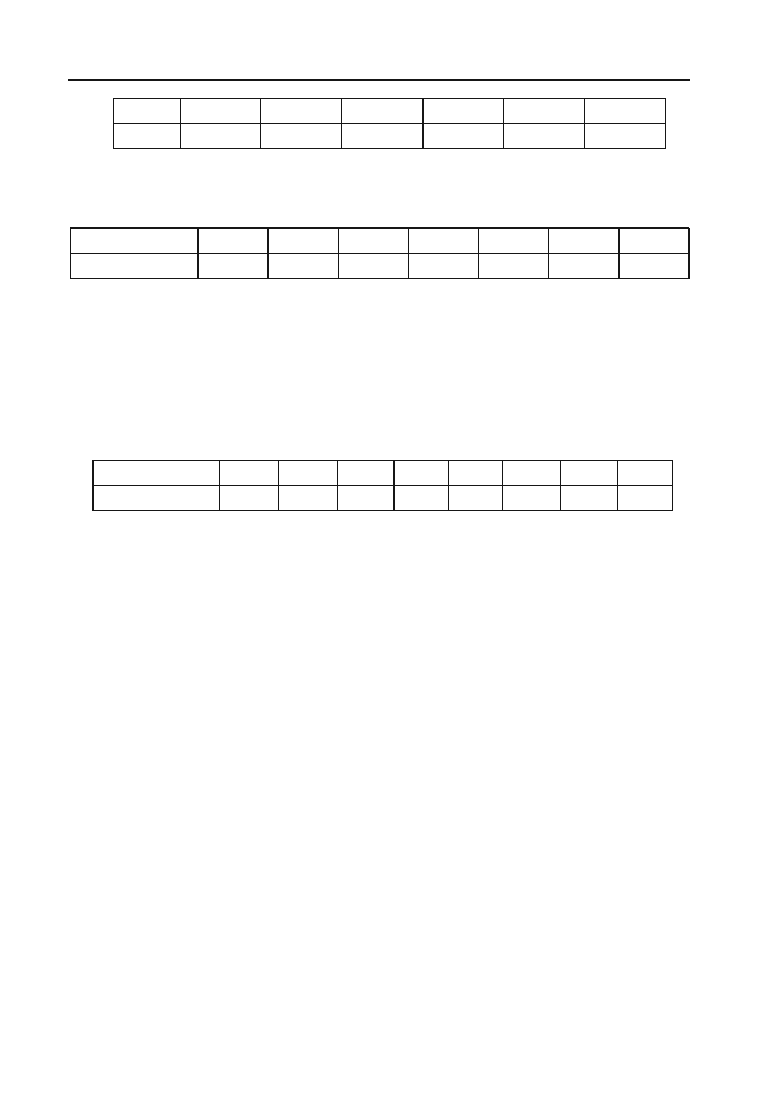
Задача 5.66.
Використовуючи метод найменших квадратів, знай+
ти емпіричну формулу
y = kx + b
для функції заданої таблицею:
360
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Задача 5.67.
На Тисменицькій хутровій фабриці є дані про
вартість продукції за сім років.
Використовуючи метод найменших квадратів, знайти параметри
функції
y = kx + b
, яка виражає динаміку зростання вартості випу+
щеної продукції на протязі семи років.
Задача 5.68.
На вугільних шахтах України середня продук+
тивність праці за перші
8
років існування незалежної держави зада+
на таблицею.
Припускаючи, що
у
від
х
залежить лінійно (
y = kx + b
), методом
найменших квадратів знайти параметри
k
i
b
. Яка буде динаміка
росту?
х –0,2 0,2 0,4 0,6 0,8 1,0
у 3,2 2,9 1,8 1,6 1,2 0,7
х (рік)
1 2 3 4 5 6 7
у (млн.грн.)
6,3 9,5 13,9 16,1 20,2 24,1 26,8
х (рік) 1 2 3 4 5 6 7 8
у (млн. грн.) 100 156 170 184 194 205 220 229
