Колесников А.А. Синергетические методы управления сложными системами: теория системного синтеза
Подождите немного. Документ загружается.


ψ
1
= x
3
+ γ
1
x
1
+ γ
2
x
2
¨x
2ψ
(t)+
γ
2
− 1+γ
1
˙x
2
2ψ
(t)
˙x
2ψ
(t)+(γ
1
− γ
2
)x
2ψ
=0.
γ
1
>γ
2
γ
2
< 1 γ
2
< 0 γ
2
1
x
2ψ
=˙x
2ψ
(t)=0
u
1
= −γ
1
1+
1
T
1
x
1
− γ
2
1+
1
T
1
x
2
−
γ
2
+
1
T
1
x
3
− γ
1
x
3
3
,
γ
1
>γ
2
> 1
ξ =
0, 5(γ
2
− 1)
√
γ
1
− γ
2
,γ
1
>γ
2
> 1.
ξ =1 γ
1
γ
2
γ
1
= γ
2
+0, 25(γ
2
− 1)
2
.
u
1
γ
1
˙x
2
2ψ
sin γ
2
x
2
cos γ
2
x
2
sin γ
2
x
2
∼
=
γ
2
x
2ψ
−
γ
3
2
6
x
3
2ψ
cos γ
2
x
2
∼
=
1 − 0, 5γ
2
2
x
2
2ψ
ψ
1
ψ
1
= x
3
+ γ
1
x
1
+ γ
2
x
2ψ
−
γ
3
2
6
x
3
2ψ
¨x
2ψ
(t)+
γ
2
1 − 0, 5γ
2
2
x
2
2ψ
− 1+γ
1
˙x
2
2ψ
(t)
˙x
2ψ
(t)+γ
1
− γ
2
)x
2ψ
+
γ
3
2
6
x
3
2ψ
=0.
ψ
1
=0 x
3
=˙x
2
(t)
¨x
3
(t)+
γ
2
− 1+3γ
1
x
2
3
˙x
3
(t)+(γ
1
− γ
2
)x
3
=0.
γ
1
< 1 γ
2
< 1 γ
2
< 0
ψ
1
ψ
1
=0
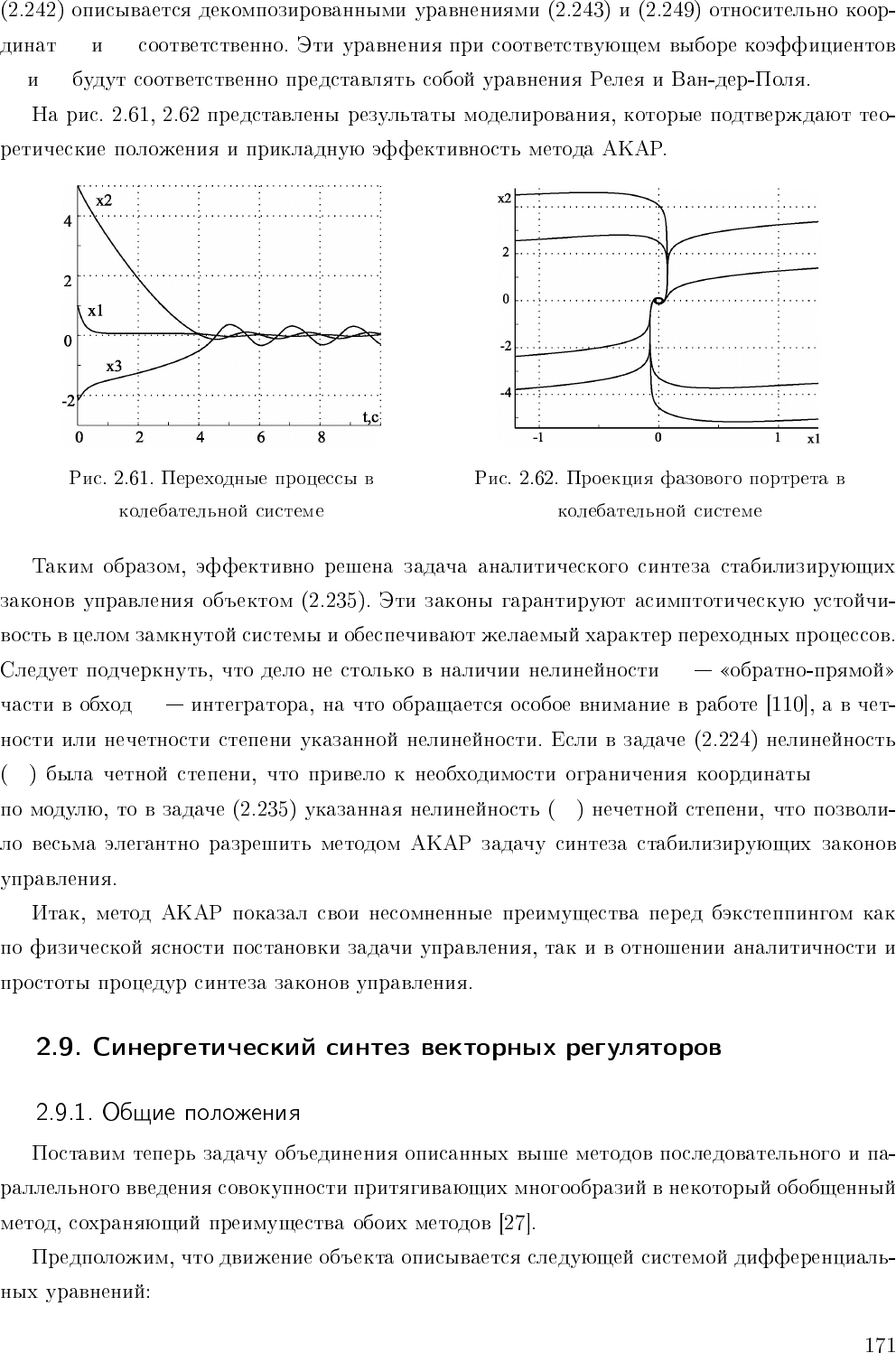
x
2
x
3
γ
1
γ
2
x
3
3
x
2
x
2
3
|x
3
| b
x
3
3

˙x
i
(t)=f
i
(x
1
,...,x
n
),i=1, 2,...,p;
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j+1
x
j+1
,j= p +1,...,µ;
˙x
s
(t)f
s
(x
1
,...,x
j
)+b
s
u
s
,s= µ +1,...,n,
x
1
,...,x
n
f(·)
u
s
(x
1
,...,x
n
)
u
s
(x
1
,...,x
n
)
ψ
s
=
n
k=1
β
sk
+ ϕ
s
(x
1
,...,x
µ
).
u
s
(x
1
,...,x
n
)
ψ
12...µ
µ
k=1
ξ
sk
x
k
+ b
sµ
ϕ
s
(x
1
,...,x
µ
)=0,
˙x
i
(t)=f
i
(x
1
,...,x
n
),i=1, 2,...,p;
˙x
j
(t)=f
j
(x
1
,...,x
j
) −
a
µ+1
ξ
µ+1
µ
k=1
ξ
sk
x
k
−
b
sµ
a
µ+1
ξ
µ+1
ϕ
s
(x
1
,...,x
µ
).
µ
u
µ1
=
b
sµ
a
µ+1
ξ
µ+1
ϕ
s
(x
1
,...,x
µ
),
ψ
µ1
=
µ−1
k=1
α
1k
x
k
+ ϕ
µ1
(x
1
,...,x
µ−1
)=0.
ψ
µ1
ψ
1...µ
u
µ2
=
a
µ
α
µ−1
+ ϕ
µ1
(x
1
,...,x
µ−1
),
u
µ2
(x
1
,...,x
µ−1
)
ψ
µ2
=
µ−2
k=1
α
2k
x
k
+ ϕ
µ2
(x
1
,...,x
µ−2
)=0.

ψ
µp
=
µ−p
k=1
α
pk
x
k
+ ϕ
µp
(x
1
,...,x
µ−p
)=0.
ψ
1...µ
=0,...,ψ
µp
=0 x
µ
,x
µ−1
,... p
˙x
i
(t)=f
i
(x
1
,...,x
p
),i=1, 2,...,p,
ψ
µ−p+1
=0
ϕ
s
ϕ
µ1
,...,ϕ
µp
β
sk
α
1k
,...,α
pk
u
s
(x
1
,...,x
n
)
ψ
1...µ
=0
u
µ
(x
1
,...,x
µ
),...,u
µ−p+1
(x
1
,...,x
µ−p+1
),
ψ
1...µ
=0
ψ
µ1
=0 ψ
µ2
=0
ψ
µp
=0
s
µ − p
p =0
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j+1
x
j+1
,j=1, 2,...,µ;
˙x
s
(t)=f
s
(x
1
,...,x
n
)+b
s
u
s
,s= µ +1,...,n,
µ
u
s
(x
1
,...,x
n
)
s ψ
s
=0
u
s
ψ
s
ψ
s
=
n
k=1
β
sk
x
k
+ ϕ
s
(x
1
,...,x
µ
).
u
s
(x
1
,...,x
n
)
ψ
1−p
=
µ
k=1
α
sk
x
k
+ b
p+1
ϕ
s
(x
1
,...,x
µ
)=0,

˙x
j
(t)=f
j
(x
1
,...,x
j
) −
a
µ+1
α
µ+1
µ
k=1
α
sk
x
k
−
β
p+1
a
µ+1
α
µ+1
ϕ
s
.
µ
µ
ψ
µ1
=
µ
k=1
γ
1k
x
k
+ ϕ
µ1
(x
1
,...,x
µ−1
)=0
ϕ
s
(x
1
,...,x
k
) ψ
µ1
=0
µ−1
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j+1
x
j+1
,j=1, 2,...,µ= n − 2;
˙x
n−1
(t)=f
n−1
(x
1
,...,x
n
)+b
2
u
n−1
;
˙x
n
(t)=f
n
(x
1
,...,x
n
)+b
1
u
n
.
ψ
1
=
n
k=1
β
1k
x
k
+ ϕ
1
(x
1
,...,x
n−2
)=0;
ψ
2
=
n
k=1
β
2k
x
k
=0,
Bb
1
u
n
= −
n−2
k=1
β
2n
β
1k
− β
1n
β
2k
+ β
2n
∂ϕ
1
∂x
k
f
n
(x
1
,...,x
k
)+
+ a
k+1
x
k+1
− Bf
n−1
−
β
2n
T
1
ψ
1
+
β
1n
T
2
ψ
1
;
Bb
2
u
n−1
=−
n−2
k=1
β
2,n−1
β
1k
−β
1,n−1
β
2k
+β
2n
∂ϕ
1
∂x
k
f
n
(x
1
,...,x
k
)+
+ a
k+1
x
k+1
− Bf
n−1
−
β
2,n−1
T
1
ψ
1
+
β
1,n−1
T
2
ψ
1
,
B = β
1,n−1
β
2n
− β
1n
β
2,n−1

ψ
1−2
=
n−1
k=1
β
1n
β
2k
− β
2n
β
1k
x
k
− β
2n
ϕ
1
(x
1
,...,x
n−2
)=0.
x
n−1
=
1
B
n−2
k=1
β
1n
β
2k
− β
2n
β
1k
x
k
−
β
2n
B
ϕ
1
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j
x
j+1
,j=1, 2,...,n−3;
˙x
n−2
(t)=f
n−2
(x
1
,...,x
n−2
)+
a
n−1
B
n−2
k=1
β
1n
β
2k
− β
2n
β
1k
x
k
−
β
2n
a
n−1
B
ϕ
1
,
ψ
1−2
ψ
µ1
=
n−2
k=1
γ
1k
x
k
+ ϕ
2
(x
1
,...,x
n−3
)=0,
..........................................,
ψ
µ,n−3
= γ
n−3,1
x
1
+ γ
n−3,2
x
2
+ ϕ
n−1
(x
1
)=0
ϕ
1
(x
1
,...,x
n−2
)
ϕ
2
(x
1
,...,x
n−3
)
ϕ
n−1
(x
1
)
ϕ
n−1
,...,ϕ
1
u
n−1
(x
1
,...,x
n
)
u
s
(x
1
,...,x
n
)
ψ
s
=0
ϕ
1
(x
1
,...,x
n−2
),...,ϕ
n−1
(x
1
)
ϕ
µ1
=0 ϕ
µ2
=0
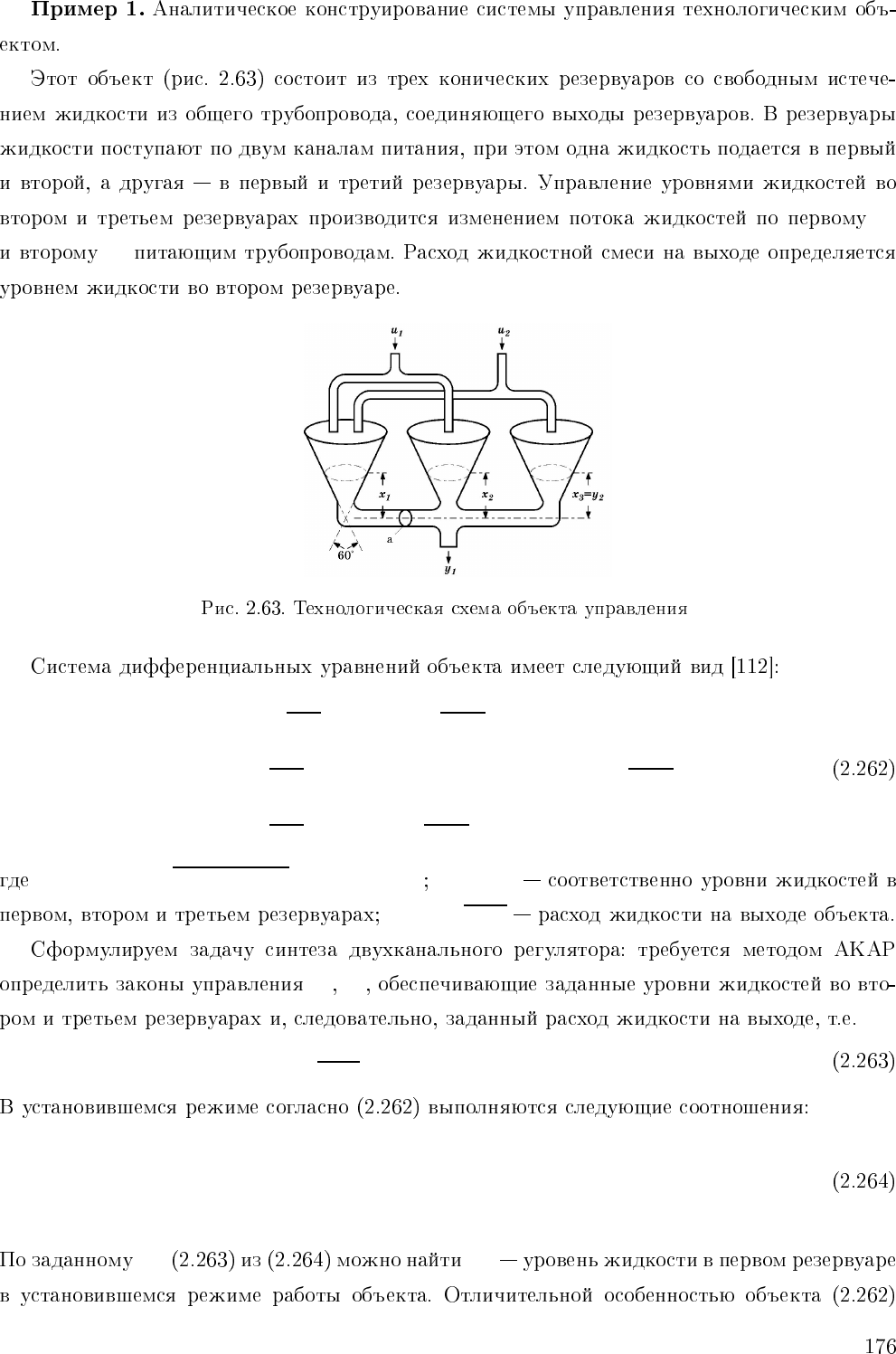
u
1
u
2
˙x
1
(t)=−
3a
πx
2
1
f(x
1
− x
2
)+
3
2πx
2
1
(u
1
+ u
2
);
˙x
2
(t)=
3a
πx
2
2
f(x
1
− x
2
) − f(x
2
− x
3
) − f(x
2
)
+
3
2πx
2
2
u
1
;
˙x
3
(t)=
3a
πx
2
3
f(x
2
− x
3
)+
3
2πx
2
3
u
2
,
f(x
i
−x
j
)=
!
2g|x
i
− x
i+1
|sign(x
i
−x
i+1
) x
1
,x
2
,x
3
y
1
= a
√
2gx
2
u
1
u
2
x
2
= x
2r
=
y
2
1r
2ga
2
; x
3
= x
3r
= y
2r
; x
1r
=1, 25x
2r
.
f(x
1r
− x
2r
)=0, 5f(x
2r
);
af(x
2r
)=u
1r
+ u
2r
= y
1r
;
af(x
2r
− x
3r
)=−0, 5u
2r
.
x
2r
x
1r

u
1
u
2
u
1
u
2
x
1
ψ
1
= α
2
(x
2
− x
2r
)+α
3
(x
3
− x
3r
);
ψ
2
= β
2
(x
2
− x
2r
)+β
3
(x
3
− x
3r
).
u
1
u
2
ψ
12
=0 ψ
1
=0 ψ
2
=0
B(x
2
− x
2r
)=0; B(x
3
− x
3r
)=0,
B = α
2
β
3
− β
2
α
3
B =0
ψ
1
ψ
2
u
1
(x
1
,x
2
,x
3
) u
2
(x
1
,x
2
,x
3
) ψ
1
ψ
2
T
1
˙
ψ
1
(t)+ψ
1
=0; T
2
˙
ψ
2
(t)+ψ
2
=0; T
1
> 0; T
2
> 0,
u
1
= −2a
f(x
1
− x
2
)−f(x
2
− x
3
)−f(x
2
)
−
2πβ
3
x
2
2
3T
1
B
ψ
1
+
3πα
3
x
2
2
3T
2
B
ψ
2
;
u
2
= −2af(x
2
− x
3
)+
2πβ
2
x
2
3
2T
1
B
ψ
1
−
2πα
2
x
2
3
3T
2
B
ψ
2
ψ
1
ψ
2
u
1
= −2a
f(x
1
− x
2
)−f(x
2
− x
3
)−f(x
2
)
−
2πx
2
2
3B
α
2
β
3
T
1
−
α
3
β
2
T
2
×
× (x
2
− x
2r
) −
2πx
2
2
α
3
β
3
3B
1
T
1
−
1
T
2
(x
3
− x
3r
);
u
2
= − 2af(x
2
− x
3
) −
2πx
2
3
3B
α
2
β
3
T
2
−
α
3
β
2
T
1
(x
3
− x
3r
)−
−
2πx
2
3
α
2
β
2
3B
1
T
2
−
1
T
1
(x
2
− x
2r
).
u
1
u
2
u
1
u
2
ψ
12
=0

ψ
12
=0 ψ
1
= ψ
2
=0 x
2
= x
2r
x
3
= x
3r
x
1
ψ
12
=0
u
1
u
2
˙x
1
(t)=−
6a
πx
2
1
f(x
2r
− x
1
) − 0, 5f(x
2r
)
.
x
1
= x
1r
v(t)=0, 5(x
1
− x
1r
)
2
.
˙v(t)
˙v(t)=−
6a(x
1
− x
1r
)
πx
2
1
f(x
1
− x
2r
) − 0, 5f(x
2r
)
.
x
1
> 0
˙v(t)
(x
1
− x
1r
)
f(x
1
− x
2r
) − 0, 5f(x
2r
)
!
2g(x
1
−x
2r
)−0, 5
!
2g|x
2r
| > 0 x
1
>x
1r
(x
1
−x
1r
) > 0
!
2g(x
1
−x
2r
)−0, 5
!
2g|x
2r
| < 0 x
1
<x
1r
(x
1
−x
1r
) < 0.
˙v(t) < 0
x
1
= x
1r
u
1
u
2
u
1
u
2
f(x
2
− x
3
)
2πx
2
2
α
3
β
3
3B
1
T
1
−
1
T
2
(x
3
− x
3r
)
2πx
2
3
α
2
β
2
3B
1
T
2
−
1
T
1
(x
2
− x
2r
).
T
1
= T
2
= T u
1
u
2
u
1
= −2a
f(x
1
− x
2
) − f(x
2
− x
3
) − f(x
2
)
−
2πx
2
2
3T
(x
2
− x
2r
);
u
2
= −2af(x
2
− x
3
) −
2πx
2
3
3T
(x
3
− x
3r
).
α
2
α
3
β
2
β
3
˙x
2
(t)=−
1
T
(x
2
− x
2r
);
˙x
3
(t)=−
1
T
(x
3
− x
3r
).
T
1
= T
2
= T u
1
u
2
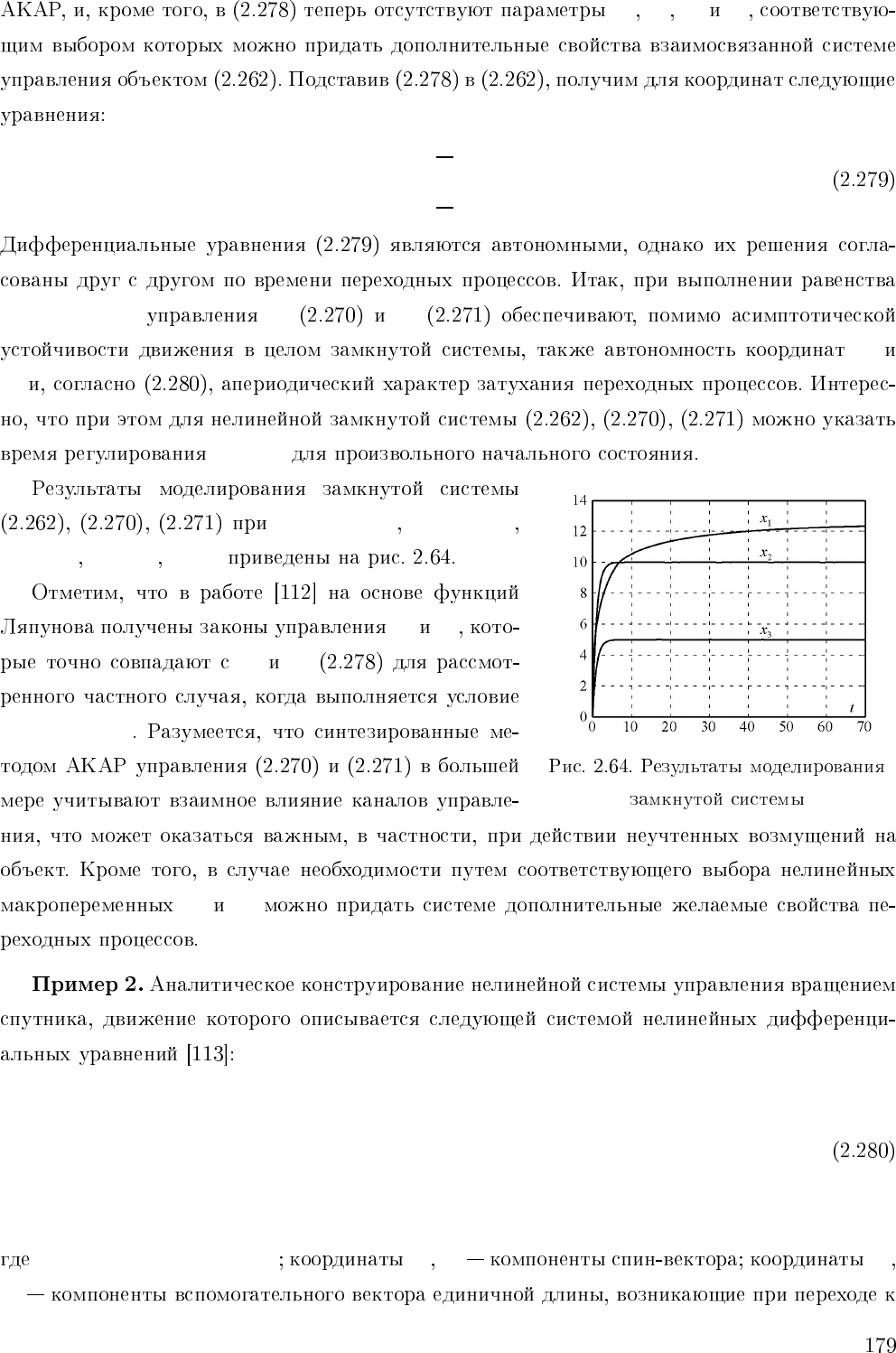
x
2
x
3
t
p
≈ 3T
T
1
= T
2
=1 x
1r
=12, 5
x
2r
=10 x
3r
=5 a =2
u
1
u
2
u
1
u
2
T
1
= T
2
= T
ψ
1
ψ
2
˙x
1
(t)=−2x
2
+ u
1
;
˙x
2
(t)=2x
1
+ u
2
;
˙x
3
(t)=−x
2
ω(x
3
,x
4
)+x
4
;
˙x
4
(t)=x
1
ω(x
3
,x
4
) − x
3
,
ω(x
3
,x
4
)=
1−x
2
3
−x
2
4
1/2
x
1
x
2
x
3
x
4
