Kothari D.P., Nagrath I.J. Modern Power Systems Analysis
Подождите немного. Документ загружается.

144
|
nrodern
Power
System
Analysis
, nlV^
-
ZrI
*l
^-* -j(at-/tx+t
'1
+Jlltrle-*ett''-tLt-rh)
I
(5.31)
The
instantaneous
voltage
consists
of two
terms
each
of which
is
a function
of two
variables-time
and
distance.
Thus
they
represent
two
travelling
waves,
characteristics
and Performance
of Power
Transmission
Lines
-
At(f
+40
Sendingendx=/
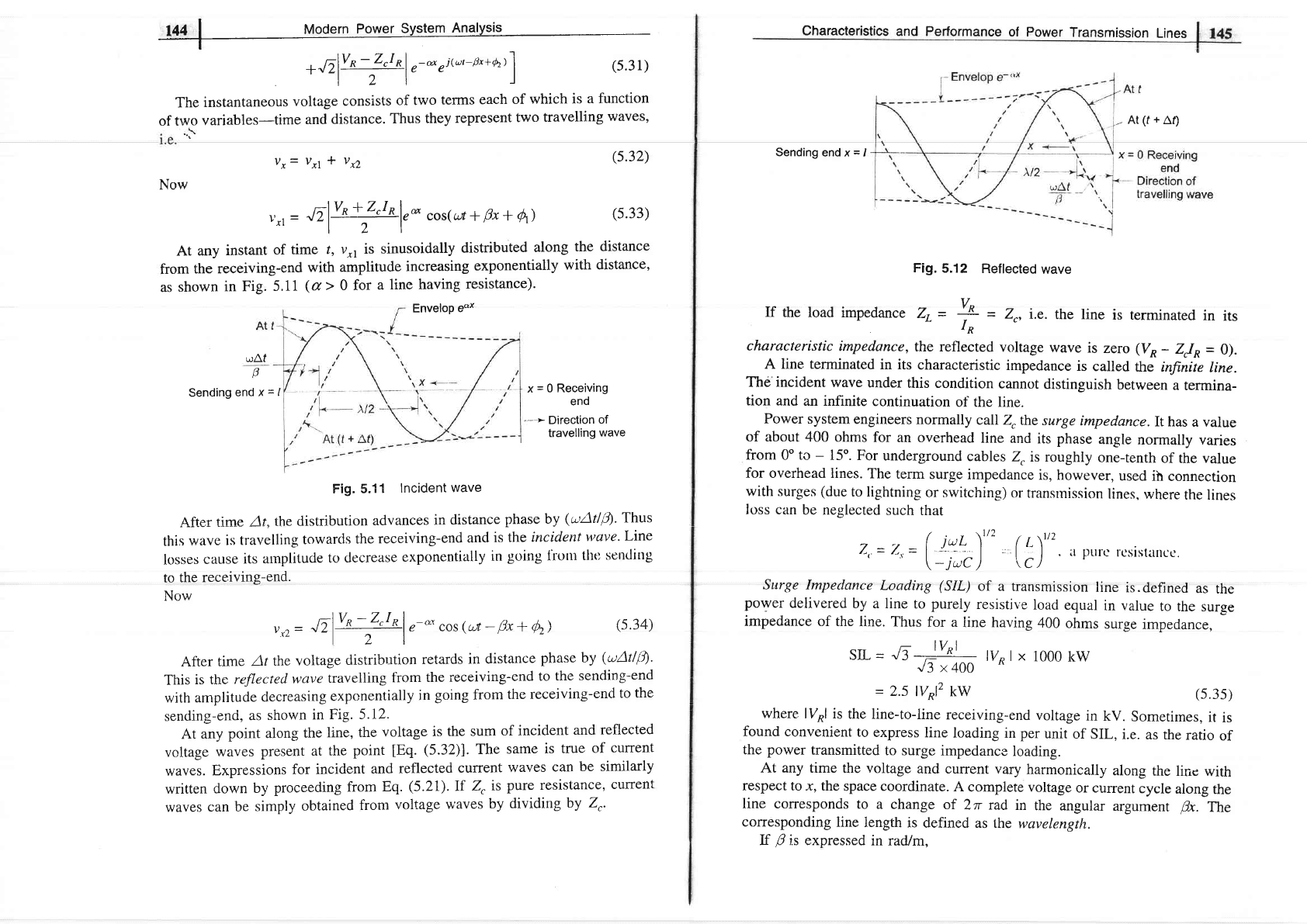
Fig.
5.12
Reflected
wave
If
the load
impedance
Zr
=
+
=
2,,
i.e.
the line
is terminated
in
its
.
IR
characteristic
impedance,
the reflected
voltage
wave
is
zero
(vn-
zJn=
0).
A line terminated
in its
characteristic
impedance
is
called
the infinite
line.
The incident
wave
under
this condition
cannot
distinguish
between
a
termina-
tion and
an infinite
continuation
of the line.
Power
system
engineers
normally
caII
Zrthe
surge
impedance.
It has
a value
of about 400 ohms
for
an overhead
line
and
its
phase
angle
normally varies
from 0" to
-
15o. For
underground
cables
Z.
is roughly
one-tenth
of the value
for overhead lines.
The
term
surge
impedance
is, however,
used
ih
connection
with surges
(due
to lightning
or switching)
or
transmission
lines.
where
the lines
loss
can
be neglected
such that
(
;,.,1
rl/2 i/1
z,
=
z,=
l:i:r)
(;)"'.
,, purc
rcsist''cc
SLtrge Impetlance
Loading
(SIL)
of a transmission
line
is.defined
as
the
power
delivered
by a line
to
purely
resistive
load
equal
in value
to
the surge
impedance
of the
line.
Thus
for a
line having
400
ohms
surge
impedance,
Now
At
any
instant
of
time
t, v.rl
is
sinusoidally
distributed
along
the
distance
from
the
receiving-end
with
amplitude
increasing
exponentially
with
distance,
as
shown
in Fig.
5.11
(a
> 0 for
a
line
having
resistance).
Envelop
eox
u-rAf
B
Sendingendx=/
-x=0Receiving
end
-'-
'
Direction
of
travelling
wave
Fig.
5.11
lncident
wave
After
t-ime
At,
the distribution
advances
in
distance
phase
by
(u'Atlfl.
Thus
this
wave
is
travelling
towarcls
the
receiving-end
and
is
the
incident
v'ave'Line
losses
cause
its arnplitucle
to
decrease
exponentially
in
gcling
l}onr
tht:
sendirlg
to the
receiving-end.
Now
Vx=
Vrl
*
VxZ
"',,
-
JIlh-?\,*
"or{'l
+
gx
+
h)
u,r=
Elt+tlu^
cos
(az
-
0x+
dz)
(s.32)
(5.33)
(s.34)
After
time
At
the
voltage
distribr-rtion
retards
in
distance
phase
by
(uAtl4.
This
is the
reflecterl
wave
travelling
trom
the
receiving-end
to
the sending-end
with
amplitude
decreasing
exponentially
in
going from
the receiving-end
to the
sending-end,
as
shown
in
Fig' 5.12.
At
any
point along
the
line, the
voltage
is
the sum
of incident
and
reflected
voltage
waves
present
at
the
point
tEq.
(5.32)1.
The
same is
true
of
current
waves.
Expressions
for
incident
and
reflected
current
waves
can
be similarly
written
down
by
proceeding
from
Eq.
(5.21).If
Z"
is
pure resistance,
current
waves
can
be
simply
obtained
from
voltage
waves
by
dividingby
Zr.
where
lVol is
the line-to-line
receiving-end
voltage
in
kV.
Sometirnes,
it
is
found
convenient
to
express
line
loading
in
per
unit
of
SIL,
i.e.
as the
ratio
of
the
power
transmitted
to
surge impedance
loading.
At
any time
the
voltage
and current
vary
harmonically
along
the
linc
with
respect
to x, the
space coordinate.
A
complete voltage
or current
cycle
along
the
line
corresponds
to
a change
of
2r rad
in
the
angular
argument
Bx.
The
corresponding
line
length
is
defined as the
wavelength.
It
0
i.s expressed
in radlm,
SIL
=
JT
-y!-
tv,
I
x
t00o
kw
J3
x
aoo
lvo
I
x
looo
k
=
2.5
lyRl2 kw
(s.3s)

-iAd
I
Modern
Po*g!Sy$e!l
Anelysis
)-Zn/gm
(s.36)
Now
for
a typical
power
transmission
line
g
(shunt
conductancelunit
length)
=
0
'
=
*fu=
velocitv
of
light
The
actual
velocity
of
the
propagation
somewhat
less
than
the
velocity
of
light'
.,
=
1"
lot
=
6,000
km
"- 50-
Practical
transmission
lines
are
much
shorter
than
this
(usually
a few
hundred
kilometre
s).
It
needs
to
be
pointed
out
heye
that
the
vyaves
tlrau'tt
in
Figs,5.11and5.]'2areforitlustrationonlyanddonotpertainnareal
power
transmission
line'
A
three-phase
50
Hz
transmission
line
is
400
km
long'
The
voltage
at the
sending.en
d
ts
220kV.
The
line
parameters
are
r
=
o.!25
ohnr/km,
x
=
0.4
ohm/
tm
ani
y
=
2.8
x
10-6
rnho/km'
Find
the
following:
(i)Thesending-enclcurrentandrebeiving-endvoltagewhenthereisno-load
Solution
The
total
line
parameters
are:
R
-
0.125
x
400
=
50.0
f)
X
=
O.4
x
400
=
160'0
fl
Y
=
2.8
x 10-6
x
400
lg)"
-
l'12
x
IA-3
lxf
U
Z=
R+
iX=
(50'0
+
j160'0)
=
168'0
172'6"
Q
YZ
=
l.l2
x 1O-3
/90"
x
168
172'6"
=
0.188
1162'6"
(i)
At
no-load
Vs=
AVn'
ls
=
CVa
A
and
C
are
comPuted
as
follows:
ll
A
=
l*
t
YZ
=
l+
*x
0.188
1162',6"
/L-
)
2
=
0.91
+
j0.028
147
(s.42)
of
wave
along
the
line
would
be
7=
(yz)1/2
=
Qu,C(r
+
juL))rt2
-
iu
(LQ'''
(r-
t
i)'''
7=
a+
jg
=
ju\Lc),,,(t-
t#)
Now time
for a
phase
change
of
2n is 1f
s, where/=
cul2r
is
the frequency
in
cycles/s.
During
this
time
the
wave
travels
a distance
equal
to
). i.e.
one
wavelensth.
r
(
C\ltz
a--l-l
2\L)
0
=
a
(Lq'''
C_
2ffi0
\
Velocity of
propagation
of
wave, ,
=
-4=:
f^
m/s
'
"'
ri
f
which is
a well
known
result.
For
a lossless
transmission
line
(R
=
0, G
=
0),
,=
7yz)'''
-
iu(LC)tlz
such
that
e.
=
A,
0
=
.
(Lq'''
)-2110-
,?n=,=:
1,,-
m
and
v
=
fA
=
ll(LC)rlz
m|s
For
a single-phase
transmission
line
L=
lto
,n
D
2r
r'
(s.37)
(s.38)
(5.3e)
(s.40)
(s.41)
ln D/r
v=4'
(Pol^D
2*o
)t/2
'
It;,.t-
'l
t"nG
)
Since
r and
rt
are
quite close
to
each
other,
when
log is
taken,
it
is sufficiently
accurate
to
assume
that ln
q,
=
h
D/r.

'
lvnhn'
=
#:#
=
242
kY
115
l=
lcl lVRl
=
1.09 x
10-3x
ry
*
103
=
152
A
"J3
It is to
be
noted
that under
no-load
conditions,
the
receiving-end
voltage
(242
kV)
is
more than
the
sending-end
voltage.
This
phenomenon
is known
as
the
Ferranti
elfect
and
is
discussed
at length
in
Sec.
5.6.
(ii)
Maximum permissible
no-load
receiving-end
voltage
=
235 kv.
,r, lV"l
220
^,
=l%l:ffi=0.e36
Now
1
A=l+LYZ
2
1^
=
1 +
-;
t',
.i2.8
x
10-6 x
(0.125
+
70.4)
z
=
(1
-
0._56
x
t0-6P1
+
j0.t75
x
r0-6P
,l
th
of the real part.
lzll can
be
Since
thc irnaginary
part
will
bc less
than,
approxirnated
as
.
r14E
-f
Modern
Power
Svstem
Analvsis
lAl
=
0.91
C
=
Y(l +
YZ/6)
=
=
1.09 x
10-3
I
Characteristics.
and
Performance
of
Power
Transmission
Lines
I
14g^
t-
simplifying,
we
obtain
the
maximum
permissible
frequency
as
f
=
57.9
Hz
If in
Example
5.5
the
line
is
open
circuited
with
a receiving-end
voltag
e
of 220
kV,
find
the
rms
value
and phase
angle
of
the
following:
(a)
The
incident
and
reflected
voltages
to
neutral
at
the
receiving-end.
(b)
The
incident
and
reflected
voltages
to
neutral
at
200
km
from
the
receiving-end.
(c)
The
resultant
voltage
at
200
km
from
the
receiving-end.
Note:
Use
the
receiving-end
line
to
neutral
voltage
as
reference.
solution
From
Example
5.5,
we
have
following
line parameters:
r
=
0.725
Qlkm;
x
=
0.4
Olkm; y
=
j2.g
x
10{ Uncm
z
=
(0.125
+
j0.4)
Olkm
=
0.42
172.6
CI/km
y-
1yz)t'2
=
(2.8
x
10-6 x
0.42
/.(g0
+
72.6))t/2
=
1.08
x
10-3
lgI.3
=
(0.163
+
i1.068)
x
tO--r
-
0+
j{J
a=
0.163
x
tO-3;
f=
1.06g
x
l0-3
(a)
At
the
receiving-end;
For
open
circuit
1n
=
0
;
Incident
vcrltage
-
Vn
I
?cl
n
-
2
-
220/J3
=
63.51
2
Reflected
voltage
-
vR-zclR
-
)
=
63.51
10"
kV
(to
neurral)
At 200
km
from
the
receiving-end:
l/l
Incident
voltage
=
:!u+urltlxl
2
lr:2oo
rm
=
63.51
exp
(0.163
x
l0-3 x
200)
x
exp
01.068
x
10-3
x
200)
lAl=
|
-
0.56
x
lrJ6P
=
0.936
p
_
r-0.936
0.56
x
l0
6
/=
338
km
=
0.88
V,,
VR
10"
kV
(to
neurral)
;;,,
,A,
=
220
250
I
A-l*;xi1.l2xl0-3x
Neglecting
the
imaginary part,
we can
write
(b)
L(
to+160,.I)
J0\
s0)
tAl
=
1
-
+"
r.r2
x1o-3
x
160 x
&=
0.88

ffi0'.
I
Modern
Po*e,
System Anatysis
f
=
65.62
112.2" kV
(to
neutral)
Reflected voltage
-
Ys-"-'ur-itt'l
2 l'
,,,n,u-
characteristics
and
performance
of
power
Transmission
Lines
I rsr
/v^,\
-
I
i.
u"'J
and
turns
rhrough
a
positive
angle
pr
(represenred
by phasor
oB);
while
the
reflected
voltage
wave
decreases
in
magnitude
exponentiaily
-Y-E-
--u,
=
6I.47 l-12.2"
kV
(to
neutral)
(c)
Resultant voltage
at 200
km from the receiving-end
-
65.62 112.2"
+ 61.47
I
-
12.2"
=
124.2 +
j0.877
=
124.2 10.4"
Resultant
line-to-line
voltage
at 200 km
=
124.2
x
J3
-
215.1
kV
5.6
FERRANTI
EFFECT
As
has
been illustrated
in Exarnple
5.5,
the
eff'ect of the line
capacitance is to
cause
the no-load
receiving-end
voltage
to be
more
than
the sending-end
voltage.
The effect
becomes
more
pronounced
as the line
length increases.
This
phenomenon
is known
as the Ferranti.
effect.
A
general
explanation of this
effect
is advanced
below:
Substituting
x
=
/ and
In
=
0
(no-load)
in Eq.
(5.21),
we
have
t/-
75
-
Vn
,at4gt *
(<
A2\
\J.-tJ
I
-
lncreasino /
-\.-
Locus of V5
wlth /
D
Vpfor I
=
0
It
is
apparent
from
the geometry
of
this
figure
that
the
resultant
phasor
voltage
Vs
QF)
is
such
that
lVol
>
lysl.
A
simple
explanation
of
the
Ferranti
effect
on
an
approximate
basis
can
be
advanced
by
lumping
the
inductance
and
capacitance
parameters
of
the
line.
As
shown
in
Fig.5.14
the
capacitance
is
lumpld
at
the
ieceiving-end
of
the
line.
Fig.
5.14
Here
Ir=
,
V,
(-+-.
\
juCt
)
Since
c is
small
compared
to
L,
uLl
can
be
neglected
in
comparisoh
to
yc,tl.
Thus
Vn
,-at
--ifl
2
Now
Magnitude
of
voltage
rise
_
lvrltJ
CLf
15
-
jVruCl
Vn=
Vs
-
Is
QwLl)
=
V,
+
V,tj
CLlz
=
vs0+
Jctt2)
=olv.rt+
(s.M)
(s.4s)
Increasing /
Fig.
5.13
The
above equation
shows that at
I
=
0, the incident
(E,o)
and reflected
(E
o)
voltage
waves
are both equal to
V^/2. With
reference
to Fig. 5.13,
as I
increases,
the incident
voltage wave
increases
exponentially
in magnitude
where
v
=
7/J
LC.
i1
the
velocity
of propagation
of
the
electromagnetic
wave
along
the
line,
which
is
nearly
equal
to
trr"
velocity
of
light.
5.7
TUNED
POWER
LINES
Equation
(5-23)
characterizes
the performance
of
a long
line.
For
an
overhead
line
shunt
conductance
G is
always
negligible
and
it
is
sufficiently
accurate
to
neglect
line
resistance
R
as
well.
with
this
approximation
7- Jyz
=
jalLC
cosh
7/
=
cosh
jwlJTC
=
cos
Lt,lrc
\
En= Ero= Vpl2

;fiTi I
I
uooern
power
system
Rnarysis
sinh
?/
=
sinh
jalJ-LC
=
j
sin
wtJLC
Hence
Eq.
(5.23)
simplifies
to
cos
ulJ
LC
jZ,
sin utJE
T.
r
sin
a'tJ
LC
cos
utE
Z,
eharacteristics
and
performance
of
power
Tr@
t-
Z
=
Z,
sinhl/
=
=
!
.o,nh..,tt2
_1
=
Y
ganh1il2)
t(-tU
2)
_
_
___{l
(5.48)
Now
if
alJtC
=
hr,
n
=
I,2,3,
...
lV5l
=
lVpl
llsl
=
llal
i.e.
the
receiving-end
voltage
and
current
are
numerically
equal
to
the
colresponding
sending-end
values,
so
that
there
is no
voltage
drop
on load.
Such
a line
is
called
a tuned
line.
For
50 Hz,
the length
of line
for
tuning
is
1-
--!r_.
2nrf J
LC
Since
ll^frc
=
y,
the velocity
of light
Fig.
5.15
Equivarent-z
network
of
a
transmission
rine
For
a
zr-network
shown
in
Fig.
5.15
[refer
ro
Eq.
(5.13)].
,,1
_
|
(t.
It,t,)
z,
.Jru.
,
Lr,J
-
Lr,(,
+!v,2,)
(r*ir,r,)lL,_)
According
to
exact
solurion
of
a
long
line
[refer
to
Eq.
(5.23)].
fi:I
=
filH;':"!
l'lt,^t
L
1,
_,
I
z,
___..
.
cosh
7/
JLl^
J
For
exact
equivalence,
we
must
have
Z/=
Z,
sin
h
7/
f *
*YtZ=cosh
7/
2
From
Eq.
(5.50)
Z'
=
,l-:.
sinn
1/
=
Z,
tlnh
''
:
z[*init
rr
1
vY
tJyz
-(
7t )
11-"''
-sln!-24
is
thc
fitct.r
by
which
thc
scrics
irupcdunce
ol'the
no'ri'al-z
must
be
multiplied
to
obtain
the
z parameter
of
the
equivalent-a
Substituting
7
from
Eq.
(5.50)
in
Eq.
(5.51),
we
ger
I
1
*
;
YtZ,
sitrh
7/
=
cosh
fl
r=
+@))=
,i^,^,?rx...
=
3,000
km,
6,000
km,...
(s.47)
(s.4e)
(s.s0)
(s.51)
(5.52)
It
is too
long
a
distance
of transmission
frorn
the point
of view
of cost
and
efficiency
(note
that line
resistance
was
neglected
in
the
above
analysis).
For
a
given
line,
length
and freouency
tuning
can
be
aehieved
by
increa-sing
L or
C, i.e.
by adding
series
inductances
or
shunt
capacitances
at
several places
along
the
line length.
The method
is
impractical
and
uneconomical
for power
frequency
lines
ancl
is adopted
for
tclephony
where
higher
frecluencies
are
employed.
A
method
of tuning
power
lines
which
is being
presently
experimented
with,
uses
series
capacitors
to
cancel
the effect
of the
line
inductance
and
shunt
inductors
to
neutralize
line
capacitance.
A long
line
is
divided
into
several
sections
which
are
individuatly
tuned.
However,
so far
the practical
method
of
improving
line
regulation
and power
transfer
capacity
is to
add
series
capacitors
to
reduce
line
inductance;
shunt
capacitors
under
heavy
load
conditions;
and
shunt
inductors
under
light
or no-load
conditions.
5.8
THE
EOUIVALENT
CIRCUIT
OF
A LONG
LINE
So far
as the
end
conditions
are
concerned,
the exact
equivalent
circuit
of a
transmission
line
can
be established
in
the
form
of a
T- or
zr-network.
The
parameters
of the equivalent
network
are
easily
obtained
by comparing
the
perfbrmance
equations
of a z--network
and
a transmission
line
in terms
of
end
quantities.
Lv,-
2
(s.53)

Wl
Modern
Power System
Anqlysis
I
d
(tanhfll2\.
rnus
I
is
thc lactor by which
thc shunt
aclmittancc
anr ol'
the
\ il/z )
nominal-n-must
be multiplied to
obtain the
shunt
parameter
(Ytl2)
of
the
equivalent-
z.
/1\l
Note
that Ytl |
+
+Y'
Z'
I
: j-
sinh
7/
is
a consistent equation
in terms
of the
\4)2,
above
values of Y/and
Z/.
For
a line of medium
length
tuth-l!/2
-
1 and
sinh
7/
=
1 so
that the
fll2
1t
equivalent- n- network
reduces to
that
of
nominal-n-.
Fig. 5.16'
Equivalent-T network
of a transmission
line
Equivalent-T
network
parameters
of a
transmission
line are
obtained
on
similar
lines. The equivalent-T
network
is shown
in Fig. 5.16.
As we shall
see in Chapter
6 equivalent-r
(or
nominal-r)
network is
easily
^.1^^+^l +^ l^^.1 {'l^,r, otrr.lioo o-.1 io f}roref'nro rrnirrprcqll.,
pmnlnrrerl
<fllIWPLVLT
L\J l\-rat.l
llLrW JLUUM
qllu
lot lltvlvlvlvt
(4lrl
v vrLtqrrJ
vr^lHrvJ
vs'
Z= 10-' 190"
U
Leceiving-end
load
is 50 MW
at ?20
kV,0.8
pf
lagging.
1o
=
,=-+ -
l-36.9"
=
0.164
l-36.9"
kA
J3
x220x0.8
A 50
Hz transmission
line
300 km long
has a
total
series
impedance
of
40
+
j125
ohms
and a total shunt
admittance
of 10-3
mho. The receiving-end
load
is
50
MW at220
kV with 0.8
lagging
power
factor.
Find the sending-end
voltage,
current,
power
and
power
factor
using
(a)
short line
approximation,
(b)
nominal-zrmethod,
(c)
exact
transmission
line equation
lBq.
(5.27)1,
(d)
approximation
[Eq.
(5.28b)].
Compare
the results
and comment.
Solution
Z
=
40
+
iI25
-
131.2 172.3"
Q
VR=
+20
-
lz710
kv
VJ
(a)
Short
line
approximation:
Vs
=
t27
+
0.164
/._36.9
x
131.2
172.3
=
145
14.9
lYsltin"
=
25L2
kV
Is=
In=
0.764
/_-36.9
kA
Sending-end
power
factor
=
cos (4.9"
+
36.9"
_
41.g.)
=
0.745
laggrng
Sending-end
power _
JT
x
251.2
x
0.764
x
0.745
=
53.2
MW
x@)
Nominal-trmethod:
A=D=l+
!yz=.
I '
2
I
+
_x
l0-r
lg0"
x
l3l
.2
/.72.3"
=
1
+
0.0656
L162.3
=
0.93g
/_L2"
B=Z=I3L.2
172.3"
c=
v(r+!vz)=
y+
lfz
\4/4
=
0.00
|
190"
+
I
.
t0-6
1J
g0.
x
131.2
L72.3"
4
=
0.001
/.90
7s
=
0'938
1r.2
x
r27
+
r3r.2
172.3"
x
0.164
L-36.9"
=
719.7
/7.2
+
21.5
135.4"
=
73j.4
/.6.2
lVsllin"
=
238
kV
1s
=
0.001
Z90
x
127
+
0.93g
Zl.Z
x
0.164
/._
36,9"
=
0.127
l9A
+
0.154
l_35.7" =
0.13
/.16.5"
Sending-end
pf
=
cos
(16.5.
_
6.2)
=
0.9g4
leacling
Sending-endpower=
JT
*
23g
x
0.13
x
0.gg4
=
52.7
MW
(c)
Exact
transmission
line
equarions
(Eq.
(5.29)).
fl
=
al
+
jpt
=JyZ
The
Exirmple
5.7

155
| -
Modern
Power
System
4nalysis
-
=
Jro-tlgo"*l3t.zl7z.3"
=
0.0554
+
i0.3577
=
0.362
18L2"
cosh
(al
+
i
0l)
=
!k"'
lgt
+ e*t
l-Bt1
'
gl
=
a.5'fi1
(radians)-
r'6.4,g"
eo.0s54
1e0.49")
=
1.057
lzo.49"
=
0.99
+
j0.37
e4'oss4
l-20.49"
=
0.946
l-
20.49"
=
0.886
-
j0.331
gosh
7/
=
0.938
+
iO.O2
=
0.938
11.2"
sinh
7/
=
0.052
+
70.35
=
0.354
181.5"
E l3nnn" .,^
L..= 1-
:
-t-----
=
soz.2I
l- 8.85'
"
lY Y
10-'190"
A=
D
=cosh
fl
=O:938
1L.2"
t
=7:::
,lr ul"u"'
t- 8 8s"
x
0
354 tsr s'
Vs
=
0.938
11.2"
x
127 10"
+ 128.2
172.65"
x
0.164
l-36.9"-'
=
119.13
11.2"
+ 2L03
135.75"
=
136.97
16.2"
kV
lVs
hin.
=
81,23--W
C
=
Lsinh
.y/
f
x
0.354
181.5"
z,
362.211-
8.85"
=
9.77
x
104
190.4"
.\
Is=9.J7
x
lO-a 190.4"
x
127 + 0.938
11.2"
x0.164 l-36.9
=
0.124
190.4"
+
0.154"
-
35.7"
=
0.1286
115.3"
kA
Sending-end
pf
=
cos
(15.3'
-
6.2"
-
9.1")
=
0.987
leading
Sending-end
power
=
Jt
x
237.23
x
0.1286
x
0.987
=
52.15
MW
(d)
Approximation
(5.28b):
A'=
D
=
| +
|
Yz
)
characteristics
and Performance
of Power
Transmission
Lines
=
0.938
ll.2
(already
calculated
in
part
(b))
B=
z(t*!Z\=
Z+
|
yf
\
6)
6
-{-
x
1o-3
lgo"
x
(13l.D2
1144.6.
6
=
731.2
172.3
+
=
131.2
172.3"
+ 2.87
l-125.4"
=
128.5
172.7'
c=
y(w!Z')
=
o.oo1
tetr
+
\
6)
=
0.001
l9O"
]x
to{
lrgo
xr3t.2
172.3"
6
Vs
=
0.938
11.2"
x
127
10" +
128.5
172.7'x
0.164
=
ll9.I3
11.2"
+ 21.07
135.8"
-
136.2
+
it4.82
=
137
16.2" kV
I Ys I
rin"
=
237 .3
kY
/s
=
0.13 116.5"
(same
as calculated
in
part
(b))
Sending-end pf
=
cos
(16.5'
-
6.2
=
10.3")
=
0.984
leading
Sending-end power
=
Jl *
?313 x
0.t3
x
0.984
=
52.58 MW
'fhe
results
are
tabulated
below:
I
-36.9"
Now
Short line
uppntximatktn
Nominal-r
Exact
Approximation
(
s.28h)
lyslhn"
25I.2
kv
I,
0J&
l-36.9"
kA
p.f,
0.745
lagging
P"
53.2 MW
238 kV
237.23
kV
o.I3
116.5"
kA
0.1286
1t5.3"
kA
0.984
leading
0.987
leading
52.7 MW
52.15
MW
?37.3
kV
0.13
1t6.5"
kA
0.984
leading
52.58
MW
Comments
We find
from the
above example
that
the
results
obtained
by
the
nominal-
zr
method
and the approximation (5.28b)
are
practically
the
same
and
are
very
close
to those obtained
by exact
calculations
(part
(c)).
On
the
other
hand
the
results
obtained
by'the
short line
approximation
are
in considerable
error.
Therefore,
ftlr
a line of this
length
(about
300
knr),
it is
sufficiently
accurate
to
use
the nominal-
r
(or
approximation
(5.28b))
which
results
in
considerable
saving
in
computational
eflort.

15El
I
Modern
Power System
Analysis
5.9
POWER
FLOW
THROUGH
A
TRANSMISSION
LINE
So
far the
transmission
line
performance
equation
was
presented
in the
form of
voltase
and
current
relationships
between
sending-and
receiving-ends.
Since
loads are more
often
expressed
in
terms of real
(wattslkW)
and
reactive
(VARs/
kVAR)
power, it is convenient
to deal
with
transmission
line
equations
in
the
form of sending-
and
receiving-end
complex
power
and
voltages.
While
the
problem of flow
of
power
in
a
general
network
will be
treated
in
the next
chapter,
the
principles involved
are
illustrated
here
through
a single
transmis-
sion
line
(2-nodel2-bus
system)
as shown
in
Fig. 5.17.
Sp
=
Pp
+lQP
Fig.5.17
A two-bus
system
Let us
take the
receiving-end
voltage
as areference
phasor
(Vn=lVRl
10")
and
let the
sending-end
voltage lead
it by
an angle
6
(Vs
=
lVsl
16).
Tlp-
angle
d
is known
as the
torque
angle
whose
significance
has
been
explained
in
Chapter
4 and
will further
be
taken
up
in Chapter
12
while
dealing
with
the
problem of
stability.
The complex
power leaving
the receiving-end
and entering
the
sending-end
of
the transmission
line can be
expressed
as
(on
per
phase
basis)
Sn
=
Pn
+
.iQn
--
Vn fn
Ss=
Ps +
iQs
=
YsI;
Receiving-
and
sending-end
currents
can, however,
t" .*pr"rsed
in terms
of
receiving-
and
sending-end
voltages
[see
Eq.
(5'1)]
as
(s.s6)
(s.s7)
characteristics
and
performance
of
power
Transmission
Lines
=
'ul'll^'
t(/r
-d)
-
l-4
v^t2
l1p
-
ay
t,
=
I
?l,r,f
tur
-
u)
-lll*lf
t@
+
6)
sn=
lvRt
t0
ti+l
vstt13-
a-l!lrv^tz{1-*t]
Similerly,
Ss=
iQs
In
the
above
equations
so
and
s, are
per
phase
complex
voltamperes,
while
v*
and
vr
are
expressed
in per
phase
volts.
If
yR
and
7,
are
expressed
in
kv
line,
then
the
three-phase
receiving-end
complex
por.,
is given
by
so
(3-phase
vA)
=
t
{l#%+191
t(
s
-r,
-
l4l
tvot2
x
to6
,, ,,
, i
'-/
-
L
Jt
*JT
lBl
.-'"'-lEl
3
L\tl-
a)F
s^
(3-phase
MVA)
=
T#
4p
-
,
-l*lvop
t1p
-
a1
(s.se)
(s.60)
Let A,
B,
D, the
transmission
Jine
constants,
be
written
as
A
=
lAl
la,
B
=
lBl
lP,
D
=
lDl lo
(since
A
=
D)
Therefore,
we
can
write
r1r
,_0)_lAlrv"r
4a_0)
t^=
l;l
tv5t
t(
rBl
'('
r,=
i+l
v,t
t(a+
6-
,-l+lvRt
t-p
Substituting
for
1o in
Eq.
(5.54)'we
get
This
indeed
is the
same
as
Eq.
(5.59).
The
same
result
holds
for
sr.
Thus
we
see
that
Eqs.
(5.58)
and
(5.59)
give
rhe
three-phase
MVA
if
vs
ina
vo
*"
expressed
in
kV
line.
If
Eq'
(5'58)
is
expressed
in
real
and
imaginary
parts,
we
can
write
the
real
and
reactive
powers
at
the
receiving_end
as
r*
=
JI]l-v^]cos
(/
-
a
-
l{l
rv^r'
cos (B-
a) (5.61)
"
tBt
v
-/
lrl
"
/1
lyslly*l
.
,n ^ lAl .__."
Qn=
ff
sin
1/
-
6t
-
lliivni'?
sin
(/-
a) (s.62)
similarly,
the
real
and
reactive
powers
at
sending-end
are
p,
=
I ?l
v,P
cos
(o-
o)-
lvsllv'l
'
lBl
J
tBicos(0*A
(5'63)
Qs
=
l*l
'ur,t
sin
(p
-
a)
-
tvsttvRt
'
pr
I
f
|
.'.,
l-srtl
(/1+
b)
6.e)
It
is
easy
to
see
from
Eq.
(5.61)
that
the
received
power
po
will
be
maximum
at
6=0
such
that
Po
(max)
=
'u:'ll^'
-t
Attv'P
v)
:
.
I Bt
lB-
c,os (/1
_
a)
(5.65)
The
corresponding
en @t
max
po
)
is
o ^
=
-l4LYry
!t
.
An=
- -fff:
-sin(0-u)
/E E A\
(J.J+/
(5.s5)
t,r=
ivr,=
-*
vR
,r=*r,
-
*ro

I
f60
|
Modern
Po*e,
Sy.t"r
Analysir
_
Thus
the
load must
draw
this much
leading
MVAR
in
order to receive
the
maximum
real
power.
Consider
now
the
special
case of a short
line
with a
series
impedance Z.
Now
A-D=I
l0:B=Z=lzlle
Substituting
these in
Eqs.
(5.61)
to
(5.64),
we
get
the
simplified
results
for
the
short line
as
t-
Equation
(5.72)
can
be
further
simplified
by
assuming
cos
6
=
r,since
dis
normally
small*.
Thus
Let
lvtl
-
lvRl
=
lAv1,
the
magnitude
of
voltage
drop
across
the
rransmission
line.
n^=
#tavl
(s.74)
The
above
short line
equation
will also
apply
for a long
line
when the line
is
replaced
by its
equivalent-r
(or
nominal-
r) and the
shunt admittances
are
lumped
with
the receiving-end
load and
sending-end generation.
In fact, this
technique
is
always used
in
the load
flow
problem
to
be treated
in the next
chapter.
From
Eq.(5.66),
the maximum
receiving-end
power
is received,
when
6
=
0
so
that
P^
(rnax)
=
lv]\Yol
Ytc's
//
tzt
tzl
po-
Yrillol
cos(g-6\-lvRP
coso
lzl
tzl
go=
lv')lY*l-sin
(d-
b)-
lv*l'
,ino
lzl
tzl
for
the
receiving-end
and for
the sending-end
ps=
lI:1.o,
e-tl1'lunl
.o,
@+6)
"
lzl
tzl
e,
_
ry_srn
d_
'u:'lI.'
sin
(d*
o
vo
lzl lzl
-
\
Now
cos d=
RllZl,
Pp
(max)
=
'tr',|,o'
-l'r-t
o
several
importanr
conclusions
that
easily
follow
from
Eqs. (5.71
)
to
(5.74)
are
enumerated
below:
I'
For
R
=
0
(which
is
a
valid
approximation
for
a
transmission
line)
the
real power
transferred
to
the
receiving-end
is proportional
to
sin
6
(=
6for
small
values
of
d
),
while
the
reactiu.
po*",
is
proportional
to
the
magnitude
of
the
voltage
drop
across
the
line.
2.
The
real
power
received
is
maximum
for
6
=
90o
and
has
a varue
lvsllvRvx.
of
course,
d is
restricted
to
varues
weil
below
90o
from
considerations
of
stability
to
be
discussed
in
Chapte
t
12.
3.
Maximum
real
power
transferred
for
a given
line (fixed
X)
can
be
increased
by
raising
its
voltage
level.
lt
is
from
this
consideration
that
voltage
levels
are
being
progressively
pushed
up
to
transmit
larger
chunks
bf
power
over
ronger
distances
wananted
ty
l*g;
;irtlln"rutirrg
stations.
For
very
long
lines
voltage
level
cannot
be
raised
beyond
the
limits
placed
'
4'1'present-day
high
voltage
technoiogy.
To
increase
power
transmitted
in
suclt
citscs,
tltc
only
choicc
is
to
reduce
the
line
reactance.
This
is
accomplished
by
adding
series
capacitors
in
the
line.
This
idea
will
be
pursued
further
in
chapter
12.
Series
capacitors
woulcl
of
c<lurse
incrcos!.
the
severity
of
line
over
voltages
under
switching
conditions.
4.
As
said
in
1
above,
the
vARs (lagging
reactive
power)
derivered
by
a line
is proportional
to
the
line
voltage
drop
and
is
independent
of
d
Therefore,
in
a transmission
system
if
the
vARs
demand
of
the
load
is
large,
the
voltage
profile
at
that
point
t-ends
to
sag
rather
sharply.
To
maintain
a
desired
voltage
profile,
the
vARs
demanJ
of
the
load
must
be
met
locally
by
employing
positive
vAR
generators
(condensers).
This
will
be
discussed
at
length
in
Sec.
5.10.
A
somewhat
more
accurate
yet
approximate
result
expressing
iine
voltage
drop
in
terms
of
active
and
rlactive
powers
can
be
written
directly
from
Eq.
(5.5),
i.e.
lAVl=
llnl
R
cos
Q
+
llol
X
sn
Q
lvRl
*small
dis
necessary
from
considerations
of
system
stability
which
will
be
discussed
at
length
in
Chapter
12.
Normally
the
resistance
of a transmission
line
is small
compared
to its
reactance
(since
it is
necessary
to maintain
a high efficiency
of transmission),
so that
0
=
tan-t xlR
=
90"; where
z
=
R
+
jx.The
receiving-end
Eqs.
(5.66)
and
(5.67)
can then
be approximated
as
(5.66)
(s.67)
(s.68)
(s.6e)
(5.70)
(s.1r)
(s.12)
i
ri
I
I
I

162
|
"odern
power
Svstem
Analvsis
=
R!ry
*
XQn
lvRl
This
result
reduces
to that
of
Eq.
(5.74)
if R
=
0.
characteristics
and
Performance
of Power
Transmission
Lines
Case
(a):
Cable impedance
=
70.05
pu.
Since cable
resistance
is zero,
there
is no
real
power
loss
in the
cable.
Hence
Pcr
t Pcz= Por
* Poz
=
40
pu
(s.75)
j Example
5.8
An interconnector
cable
links
generating
stations
1 and
2 as
shown
in Fig.
5.18.
The
desired
voltage profile
is
flat, i.e.lVrl=lVzl
=
1
pu.
The total
demands
at
the
two
buses
are
Spr=15+75Pu
Soz=
25 +
715
Pu
The
station
loads
are
equalized
by the
flow
of
power
in the
cable.
Estimate
the
torque
angle
and the
station power
factors:
(a)
for
cable
z
=
0 +
70.05
pu,
and
(b)
for
cable
Z
-
0.005
+
70.05
pu.
It is
given
rhat generator
G,
can
generate
a
maximum
of 20.0 pu
real power.
Pot= Pcz
=
20
pu
The voltage
of bus 2
is taken as
ref'erence,
i.e.
V,
10" and
1
is V1 16r.
Further,
for flat voltage profile
lVll
=
lV2l
-
L
Real
power
flow from
bus I
to bus
2
is obtained
from
recognizing
that
since
R
=
0, 0=
90".
Hence
D
_D
lvtllvl
Ps= Pn
=
-f
sin
6,
-
lxl
)
=
-SlIl
d,
0.05
or
4
=
I4.5"
vr=
I lL4'5"
From
Eq.
(5.69)
voltage
of bus
Eq.
(s.68)
by
Solution
The powers
at
the various
points
in
system
are
defined
in Fig.
5.18(a).
the
fundamental
(two-bus)
@
I
Sn.'
=
P61+
jQ61
lvlt51
Jp2
=
I-p2+
J\Jp2
I
^'
lv,l'
lv,llvl
-
Qt=
X
cosdt
-
":
-,:
x
0.e68
=
0.638
pu
U,\,J
U.UJ
(a)
From Eq.
(5.67)
f
lvtllv,l
2o=
-Tcos
d'
Reactive power
loss* in
the
cable is
c)
tv12
X
-
-
Qs
=
-
0.638
Pu
SDI
=
15
+/5
__>
Sn=5-l
(c)
Fig.
5.18 Two-bus
system
{
zo.ro
+
i16.12
V2=
1.0
lo"
QL= Qs
-
en
_
2es
_
1.276 pu
Total load
on
station 1
=
(15
+
i5)
+
(5
+
j0.638)
=
20
+
j5.638
Power
factor
at starion I
=
cos
[run-'
t'f:t')
=
0.963
lagging
\ 20)
Total load
on station
2
-
(25
+
jls)
-
(5
-
j0.638)
=20+i15.638
(b)
G)
15+j5
Q-.
-D-.riA
vu1
-,D1
'l\1D1
25
+ j1S
Reactivc
powcr
loss can
also be cornputed
as
l/l2X
=
:t
+(9.!1q)1
"
o.os=
t.z7
pu.
I
