Козлов В.Н., Куприянов В.Е., Шашихин В.Н. Управление энергетическими системами. Часть1. Теория автоматического управления
Подождите немного. Документ загружается.


5. МЕТОДЫ СИНТЕЗА РОБАСТНЫХ И АДАПТИВНЫХ СИСТЕМ
229
Как и в подразделе 5.4, предположим, что объект управления оп-
ределяется неизвестным вектором параметров τ так, что скаляр-
ный выход y
t
имеет вид:
)(
11
ξνϕτ
++
++=
tt
T
tt
Фy , (5.42)
где скалярная функция φ
t
и вектор Ф
t
доступны измерению при
любом t; ν
t+1
– белошумная случайная помеха. Пусть функционал
(
)
⎥
⎦
⎤
⎢
⎣
⎡
′
−−=
′
+
2
1
)(
τϕτ
T
ttt
ФyMJ , (5.43)
который при белошумных помехах преобразуется к виду:
()
[] []
222
2
,)(
t
T
tt
MФMJ
νσστττ
νν
=+−
′
=
′
, (5.44)
поскольку
[]
()
[
]
2
22
1
)()(
ν
στττϕξνϕττ
+
′
−=
′
−−++=
′
+
T
t
T
tttt
T
t
ФMФФMJ .
Из (5.43) и (5.44) следует, что наименьшее значение
)(
τ
′
t
J
дости-
гается на векторе τ из (5.42). Стохастически градиентная проце-
дура МСА вида (5.42) для (5.44) принимает вид:
])([
11 tt
T
ttt
T
tttt
wФyФ +−−−=
++
τϕγττ
, (5.45)
где
t
w – белошумная помеха. Обоснование процедуры (5.45) про-
водится при условии стохастической независимости случайных
величин Ф
t
. Однако поскольку Ф
t
– функция выходов динамиче-
ского ОУ, то не выполнены условия сходимости. Вместе с тем,
если ОУ линеен, то процесс Ф
t
обладает некоторыми специаль-
ными свойствами, учет которых позволяет обосновать состоя-

230
тельность оценок, получаемых процедурой МСА (5.45). Пусть
ОУ описывается уравнениями
)(),(),(
ξ
ν
τ
τ
ttt
ubya
+
∇
=
∇ , (5.46)
где ∇ ─ оператор сдвига во времени на такт назад;
() ()
(
)
(
)
(
)()
τλτλτλτλτλτλ
r
r
r
r
bbbaaa ++=+++= ...,;...1,
11
.
Введем скалярную функцию φ
t
и вектор-функцию Ф
t
соотноше-
ниями:
,)],()0,([)],()0,([
,)]0,()]0,(1[
11
11
++
++
∇−∇−∇−∇=
∇
+
∇
−
=
tt
T
t
ttt
ubbyaaФ
ubya
τττ
ϕ
(5.47)
где φ
t
– порождается коэффициентами, не зависящими от τ. В но-
вых обозначениях объект (5.63) описывается уравнением
)(
11
ξνϕτ
++
++=
tt
T
tt
Фy
.
Предположим, что управления u
t
формируются линейным регу-
лятором
tt
yu )()(
∇
=
∇
β
α
(5.48)
с известными коэффициентами:
(
)
,...1
1 p
p
αλαλλα
+++=
()
p
p
βλβλλβ
++= ...
1
.
Пусть регулятор (5.65) стабилизирующий для объекта (5.63).
Систему управления (5.63), (5.65) можно записать в виде уравне-
ний состояния:
)()()(
11
ξ
ν
τ
τ
++
+
=
ttt
BxAx ,

5. МЕТОДЫ СИНТЕЗА РОБАСТНЫХ И АДАПТИВНЫХ СИСТЕМ
231
где
;),max(;),,,,,(col
11
prsuuyyx
sttsttt
=
=
+−+−
……
матрицы
A(τ) и B(τ) получаются по методике п. 2.2. Пара (A(τ), B(τ)) –
управляема (см. подраздел 4.2), матрица A(τ) имеет собственные
числа внутри единичного круга, тогда справедлива теорема.
Теорема 5.4.1 (о состоятельности оценок, доставляемых
МСА). Пусть выполнены следующие условия:
1). Системы (5.46), (5.48) управляемы в указанном выше
смысле;
2). Регулятор (5.48) стабилизирующий для объекта (5.46);
3). Помехи ν
t
, в (5.46) и w
t
, в (5.45) независимые, белошум-
ные и выполнены условия:
[
]
[
]
0,0
=
=
tt
wMM
ν
,
[
]
[
]
2
2
2
,,
wtt
T
tt
cwMcEcwM ≤≤≤
νν
νν
;
4). Шаг γ
t
в соотношении (5.45) такой, что:
∞<++∞=++ ……
2
1
2
010
,
γγγγ
.
Тогда
τ
τ
=
∞→
t
t
lim с вероятностью 1 и в среднеквадратическом
смысле.
Таким образом, при выполнении условий теоремы имеет
место
сходимость по параметрам.
Идея доказательства теоремы состоит в следующем. Вво-
дится случайная величина:
22
tt
Δττ
=
−
, где
t
τ
, τ – соответст-
венно подстраиваемые и истинные параметры объекта управле-
ния, соответственно. Далее необходимо доказать следующую
лемму.
Лемма 5.4.1. Пусть выполнены условия теоремы. Тогда
справедливы рекуррентные неравенствадля математических ожи-
даний квадратов норм отклонений параметров от истинных зна-
чений:
(
)
2
22
T22
t+1 t t t t t t
M Δ M ΔγM Δ 2 γС γC
φ
≤−Φ −+
,
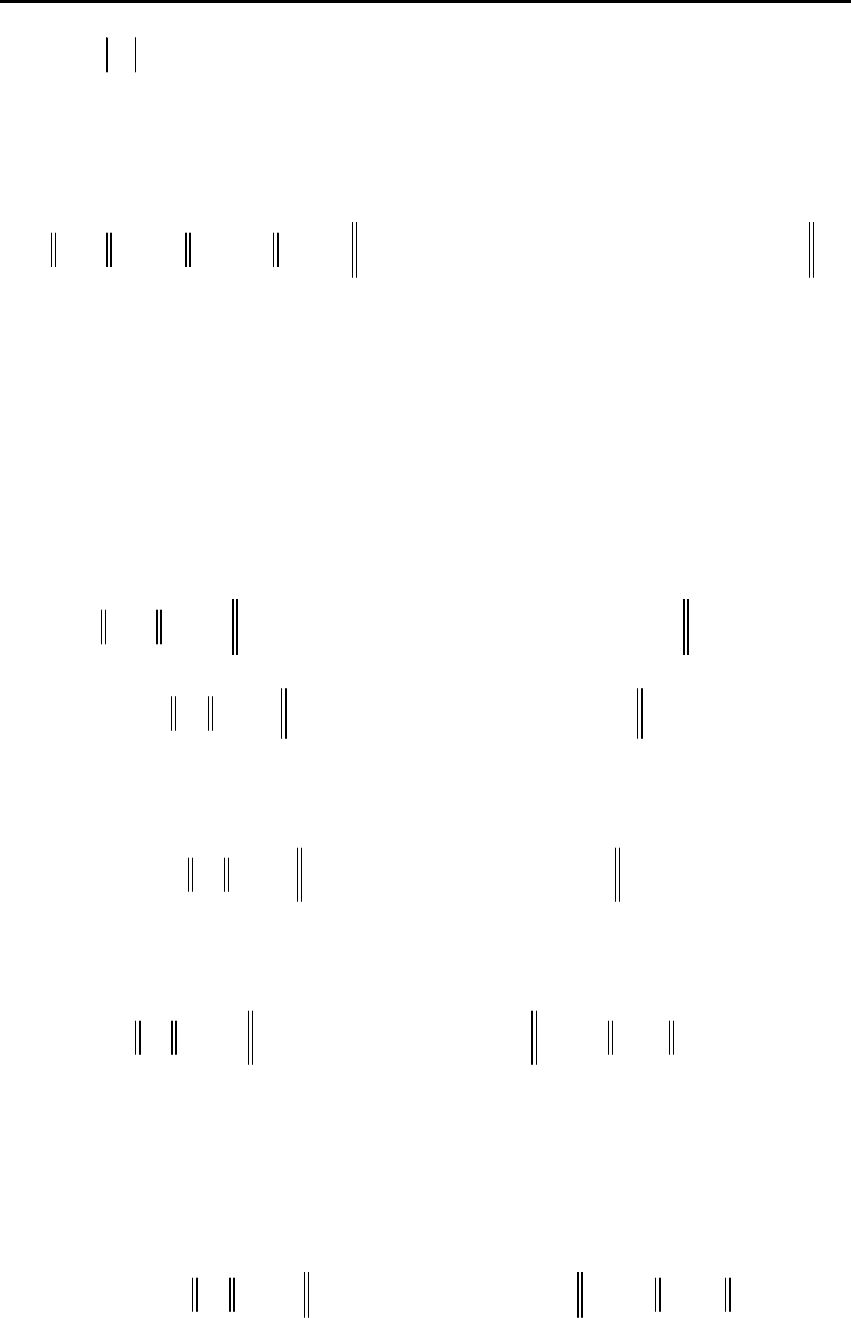
232
где
t
t
Csup
φ
=φ
,
22
vw
C=C С C
φ
+
.
Доказательство основано на рассмотрении следующей по-
следовательности соотношений для математических ожиданий:
()
2
22
T
t+1 t+1 t t t t 1 t t t t
M Δ MM y w
+
⎡⎤
=τ−τ=τ−γΦ −ϕ−Φτ+ −τ
⎣⎦
,
в которой использован алгоритм постройки параметров (5.62) ме-
тода стохастической аппроксимации. Далее в силу уравнения
объекта (5.59) в последнем соотношении вектор выхода опреде-
ляется равенством:
T
t1 t t t1
yv
++
−ϕ =φ τ+
, что приводит к следую-
щей цепочке рекуррентных равенств и неравенств:
()
()
2
2
T
t+1 t t t t t t 1 t
M Δ M Ф vw
+
⎡⎤
=τ−τ−γ Φτ−τ+ + =
⎣⎦
()
()
2
2
T
tttttt1t
= M Δ Mvw
+
⎡⎤
+−γφφτ−τ+ + +
⎣⎦
()
(
)
(
)
T
t t t t t1 t1 t
+ 2 M v w ,
++
⎡⎤
−γ φ φ τ− τ + + Δ =
⎣⎦
()
(
)
2
2
T
tttttt1t
=M M v w
+
⎡⎤
Δ+ γφ−φΔ+ + +
⎣⎦
(
)
(
)
T
tttt t1 t t
+ 2 M v w ,
+
⎡⎤
γφφΔ+ + Δ=
⎣⎦
()
(
)
2
22
T
tttttt1 tt
=M M v M w
+
⎡⎤
Δ
+γφ−φΔ+ +γ +
⎣⎦
(
)
(
)
()
T
tt tt t1 tt
+ 2 M v , w
+
⎡⎤
γφ −φΔ+ γ +
⎢⎥
⎣⎦
(
)
(
)
T
tt tt t1 t t
+ 2 M v w ,
+
⎡⎤
γφ−φΔ+ + Δ=
⎣⎦
2
22
T
tttttttt1tt
+ M M v M w
+
Δ+ −γφφΔ+γφ + γ +
(
)
T
ttt t ttt1 t t
+ 2 M v ,
+
−γ φ φ Δ + γ φ γ Δ +
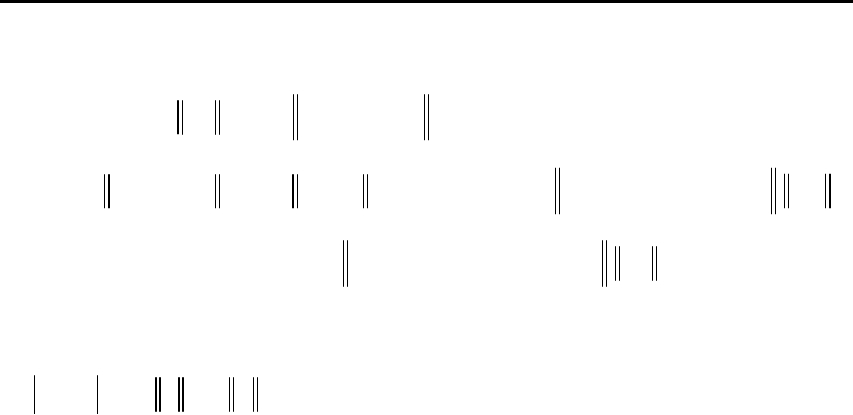
5. МЕТОДЫ СИНТЕЗА РОБАСТНЫХ И АДАПТИВНЫХ СИСТЕМ
233
(
)
T
ttt t ttt1 t t t
+ 2 M v w ,
+
γφφ Δ+γφ +γ Δ ≤
(
)
2
2
TT
t ttt t ttt t ttt1
MM 2M ,v
+
≤ Δ + γφφ Δ − γφφ Δ γφ +
22
ttt1 t t
MvMw
+
+γφ + γ +
(
)
T
tt ttt tt1 t
2M v w
+
−
γγφφΔ+φ +
T
ttt t tt1 t t
2M v w
+
+γφφΔ+φ +Δ.
При выполнении преобразований использовано неравенство:
(
)
Ma,в Ma Mb≤⋅
. Уравнения замкнутой адаптивной системы с
идентификатором имеют вид
])([,)()()(
1111 tt
T
ttt
T
ttttttt
wФyФBxAx +−−−=+=
++++
τϕγττξνττ
,
причем при выборе параметров с учетом условий теоремы имеет
место сходимость по параметрам.
5.5. Синтез адаптивных систем методом
скоростного градиента
Метод скоростного градиента позволяет синтезировать
адаптивные САУ с помощью применения эталонных моделей,
уравнений ошибки и функций Ляпунова.
5.5.1. Постановка задачи и схема синтеза. Адаптивная сис-
тема описывается уравнениями
обобщенного настраиваемого
объекта
(ОНО):
,,,)0(),,,,(/
0 nn
RRtdtd ∈∈==
τξτ
xxxxFx
где х и τ – векторы состояния и настраиваемых параметров; ξ –
вариант. Задана целевая функция контура адаптации:
()
(
)
(
)
.0,0,0,0,,,
=
≠
>=
τ
τ
τ
QQQJ xxx

234
Задано целевое условие:
(
)
0,lim
=
∞→
tQ
t
x . (5.49)
Требуется найти закон адаптации методом скоростного гради-
ента (МСГ), в котором подстройка вектора параметров τ осуще-
ствляется по алгоритму
()
[]
,),,,(grad
grad,grad
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
−=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
−=−=
ξτ
ττ
τ
ττ
t
Q
t
Q
Q
t
Q
Q
T
T
xF
x
Г
x
x
ГxГ
(5.50)
где Г>0 ─ положительно определенная матрица, в частности
N
E
γ
=Г
.
5.5.2. Синтез адаптивной САУ линейным объектом на
основе метода скоростного градиента.
Пусть ОНО описывается
линейным дифференциальным уравнением
0
00000
)0(),(])([)( xxrxxAx =+++= tb
BA
τξτξ
, (5.51)
а эталонная модель задана системой
)(
**
tb
мм
rxAx
+
=
, (5.52)
где А
*
– гурвицева матрица. Целевое условие (5.49)
()
0,
2
0
∞→
→−==
t
м
QJ xxx
τ
соответствует совпадению реакций объекта и эталонной системы
при
∞→
t
в результате подстройки параметров τ
А
и τ
В
с помощью

5. МЕТОДЫ СИНТЕЗА РОБАСТНЫХ И АДАПТИВНЫХ СИСТЕМ
235
алгоритма МСГ (5.60). Для подстройки определим ошибку
м
xxx
−
=
0
(5.53)
и дифференциальное уравнение, связывающее векторы х и х
м
.
Дифференцируя (5.53) в силу (5.51) и (5.52), получим систему
)()()()()(
**000
tbttb
мBAм
rxArrxxAxxx −
−
+
+
+=−=
τ
ξ
τ
ξ
. (5.54)
Добавляя и вычитая в правой части вектор
0*
xA
, преобразуем
уравнение (5.54) к следующему виду:
)(])([)]()([
**0*
tbb
BмA
rxxAxAxAx
−
+
+
+
−++=
τ
ξ
τ
ξ
. (5.55)
Выберем оценочную функцию xxxQ
T
P=)(
1
, где 0>=
T
PP , при-
чем матрица
Р удовлетворяет неравенству Ляпунова:
0
**
<− PAPA
T
, что имеет место, поскольку А
*
гурвицева по ус-
ловию. Алгоритм подстройки параметров на основе (5.72) при-
нимает вид:
.
)(
})(])([)]()([)(2{grad
0
***
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−=
=−+++−++−=
t
tbb
T
T
BмA
T
rxP
xxP
Г
rxxAAxAxPГ
τξτξτ
Рассмотрим теорему о сходимости процесса адаптации.
Теорема 5.5.1. Пусть выполнены следующие условия:
1). Для любых β>0,
Ξ
∈
ξ
существует константа с(β,ξ), та-
кая, что
(
)
ξβξτϕξτ
τ
,),,,(grad),,,( ctt ≤+ xxF
||;
2). Функция
),(
t
Q x при любом 0>
β
равномерно непрерыв-
на в области
}0,,{ ≥< tt
β
xx и удовлетворяет условию роста
0,),(inf ≥∞→
t
t
Q x
при
∞
→x , и функция
),(),,,(
t
Q
t
xx =
ξ
τ
ϕ

236
выпукла по τ;
3). Для любого
Ξ
∈
ξ
существуют вектор )(
**
ξ
τ
τ
= и число
0)( >=
ξ
ρ
ρ
, удовлетворяющие условию достижимости целевого
условия:
),(),,,(
*
tQt xx
ρ
ξ
τ
ϕ
−≤ . Тогда в системе достигается
цель управления.
Таким образом, для синтеза адаптивных систем можно ис-
пользовать процедуры скоростного градиента, которые соединя-
ют в себе классические методы подстройки параметров и методы
теории устойчивости. Билинейных характер управлений в ряде
случаев приводит к правым частям уравнений замкнутых систем,
которые относятся к классу
уравнений типа Лоренца, для кото-
рых возможно возникновение
хаотических режимов.
5.6. Анализ грубости методами функционального анализа
)*
Исследование грубости объектов или систем управления яв-
ляется одной из задач адаптивного управления. Исследовавное
грубости актуально в связи с неадекватностью математических
моделей, используемых при синтезе.
Проблема грубости исторически восходит к А.А. Андроно-
ву. Определенное распространение анализ грубости методами
функционального анализа получили наряду с методами исследо-
вания интервальной устойчивости полиномов по Л.В. Хар
итоно-
ву, некорректности решений, интервальной устойчивости опти-
мальных систем, с проблемой синтеза регуляторов в пространст-
ве Харди. Методы функционального анализа позволяют оценить
допустимые изменения параметров объектов и систем управле-
ния в пространстве с нормой
1,...,
|| || max | |
i
tt
in
X
X
=
=
в
n
R
, где нормы
)
∗
Написано Ю.В. Козловым и И.П. Симаковым.

5. МЕТОДЫ СИНТЕЗА РОБАСТНЫХ И АДАПТИВНЫХ СИСТЕМ
23
7
векторов и нормы операторов согласованы.
Задача 1. Пусть объект управления описываются парамет-
рически возмущенными уравнениями:
1tt t
X
HX H X
+
=
+Δ
,
где
HΔ
- матрица возмущений параметров. Требуется получить
оценки норма для матрицы возмущений параметров в нормиро-
ванном пространстве состояний.
Оценка нормы вектора правой части строится на основе
следующих соотношений:
2
1
|| || || || 4 || || || ||
ttt t
X
HX H X b ac H H X
+
=+Δ ≤− +Δ
,
связывающих нормы образов и прообразов линейных операторов,
достаточных условий сходимости:
|| || 1HH
+
Δ<
, которые опреде-
ляют ограничение на величину параметрического матричного
возмущения так, что
|| || || || 1HH
+
Δ<
. Тогда ограничения на ве-
личину нормы параметрического возмущения матрицы объекта
или системы примут следующий вид:
|| || 1 || ||
H
HΔ<−
,
|| || 1.H
<
Задача 2. Пусть система управления описываются разност-
ными уравнениями:
1ttt
X
HX FCX
+
=
+
.
Требуется получить оценку на величину нормы вектора па-
раметров обратной связи, при которой выполнены достаточные
условия устойчивости в нормированном пространстве состояний.
Оценка нормы правой части имеет вид:

238
1
|| || || || || || || || (|| || || || || ||) || ||
ttt t t
XHXFCXHFCXHFCX
+
=+ ≤+ ≤ +
,
а достаточное условие сходимости (сжатия):
|| || || || || || 1HFC+<
определяют ограничение на параметры обратной связи в виде
следующего неравенства:
|| ||
(1
|| ||
)/
|| ||
,
|| ||
1.CHFH<− <
Задача 3. Пусть система описывается уравнениями:
1
()
ttt
X
HHXFCX
+
=
+Δ +
.
Требуется сформулировать ограничение на допустимое по
условию устойчивости возмущение параметров объекта управле-
ния в виде ограничений на норму матрицы возмущений.
Ограничение на норму матричного параметрического воз-
мущения имеет вид:
|| || (1 || ||) || || || ||
H
HFCΔ<−
.
Последнее соотношение следует из оценки нормы возму-
щенного оператора замкнутой системы и достаточного условия
устойчивости.
Задача 4 (об оценках-ограничениях на собственные числа).
Пусть система управления описывается уравнениями
1
()
ttt
XHHXFCX
+
=+Δ +
.
Требуется сформулировать оценки на собственные числа
матрицы объекта управления, исходя из достаточных условий ус-
тойчивости замкнутой системы управления.
Для получения необходимой оценки требуется рассмотреть
достаточные условия рассматриваемой системы при условии
приведения матрицы системы к форме Жордана. В результате
