Козлов В.Н. Системный анализ и принятие решений
Подождите немного. Документ загружается.

201
символ определяет объединение по ем вс
∫
; символ
1
x
∈
x множеству
A
о епень принадлежностистозначает, чт
(
A
)
x
x
μ
равна
A
()
x
μ
.
Определение 2. Нечеткое число
A
на
прямой называется
выпуклым числом, если для каких-
либо реальных чисел
действительной
нечетким
,
x
yz
≤
≤
справедл
1
,,xyz
∈
иво соотношение
(
)
() min (), ()
AA
yx
μμμ
≥
A
z
. (6)
Определение 3. Нечеткое число
A
нечетким
на действительной
прямой называется
нормальным числом, если
(m
A
ax )x 1
μ
= .
Согласно определениям нечеткие числа являются
ф кциям , поэтому они могут быть изображены
графически.
Введем некоторые
опера над нечеткими числами.
Пусть
ун и аргумента
x
ции
A
и
B
– нечеткие числа на числовой прям . Выполним
гипотетическую операцию «
ой
1
∗
» над нечеткими чи ами сл
A
и
B
с
п ния:
омощью соотноше
(
)
min ( ) ( ) ( )
AB
A
Bxx
μμ
∗= ∗
∫
xy
. (7)
Если символическую операцию «» заменить
арифметическими операц чим
арифметические
о нечеткими числами:
ение:
∗
иями, то полу
перации над двумя
слож
(
)
min ( ) ( ) ( )
AB
A
Bxxx
y
μμ
+= +
∫
; (8)
вычитание:
(
)
min ( ) ( ) ( )
AB
A
Bxx
μμ
−= −
∫
xy
; (9)
умножение:
(
)
min ( ) ( ) ( )
AB
A
Bxxx
μμ
×= ×
∫
; (10)
y

(
)
min ( ) ( ) (
AB
дел е:
ени
)
A
Bxxx
μμ
=
∫
(11)
В
y
.
веденные операции пригодны для любых нечетких чисел,
и, в
ки
рых можно опре
известны ее границы, можно использовать другой подход.
исло « » назовем
гран
принадлежности,
если выполнены следующие соотношения:
частности, для
дискретных нечет х чисел, однако они
громоздки. Для
непрерывных нечетких чисел, функцию
принадлежности кото делить в условиях, когда
Определение 4. Ч ицей функции
a
()a 0,
δ
μ
∀=
()0a ,
μ
δ
−
=
()0a
μ
δ
+
≠
. (12)
Функции принадлежности имеют две границы: нижнюю - и
верхн по
к
a
юю -
b
, этому нормальное выпуклое нечет ое число
имеет вид
() (),
Ab
aA
A
xax bxx=− +−
∫∫
(13)
где
a
,
b
- нижняя и верхняя границы функции
принадлежности
Например, нечеткое число
. 2 -
2
,
приблизительно
когда
1a
=
,
3b
=
можно представить в виде:
23
12
1) (3)/2(
x
x+
числами.
Рассмотрим алгебраические операции над нечеткими числами,
расш именение подхода.
« » – символ двухместной операции, а
xx−
∫∫
.
2. Алгебраические операции над нечеткими
=−
иряющими пр
∗
A
и
B
Пусть –
непре альные выпуклые нечеткие ч
результат ерации «
рывные норм ис а. Тогда л
оп
∗
» над нечеткими числами
следу
имеет
ющий вид:
202

()/ ()/()/
Bb
B
AA B
aA aB
A
()/
Ab
()/ ()/ ,
AB b
AB B
aAB
A
B xx xxxx
μ μμ
′
⎞⎛⎞
∗ ∗ +
⎟⎜⎟
⎝⎠⎝⎠
∫∫
∫
xx
μ
⎛
= + =
⎜
∫∫
xx xx
μμ
′′
∗
∗∗
′′
∗
=+
∫
(14)
причем
a
′′
и
b
′
′
получают из
a
и
b
;
a
′
и
b
′
– в зависимости от
конкр яетной операции, функци
A
B
μ
∗
определяется также в
зависимости от операции и нормировки
μ
.
Рассм ечеткими отрим арифметические операции с н
числами.
а)
сложение нечетких чисел определяет их сумму:
Ab Bb
()/ ()/ ()/ ()/
()/ ()/ ,
AA BB
aA aB
cb
cc
ac
A
B
′
+=xxxx xxxx
xx xxc
μμ μμ
μμ
′
′′
′′
⎛⎞⎛⎞
+++
⎜⎟⎜⎟
⎝⎠⎝⎠
+=
∫∫ ∫∫
∫∫
=
(15)
=
cAB=+,
aaa
′′ ′
=+
,
bbb
′′ ′
=+
.
Функцию
c
μ
будем искать виде
12
c
k k
в
x
μ
=
+
. Ис я из
нормировки, имеем:
ход
для
axc
′′
≤≤
:
12
12
12
,,;
0
c
kk
ka k
ca ca ca
μ
⇒= =− =
⎨
′′
1
1
kc k
axa
+=
′′ ′′
⎧
−
′
′′′′′
+=
−−−
⎩
для
cxb
′′
≤≤
:
12
12
12
1
,,.
0
c
kk
kb k
cb cb cb
μ
⇒= =−
⎨
′′
′′
+=
−−−
⎩
Таким образ
1kc k+=
⎧
bxb
′′ ′′
−
=
′′
ом, имеет место следующий результат
203
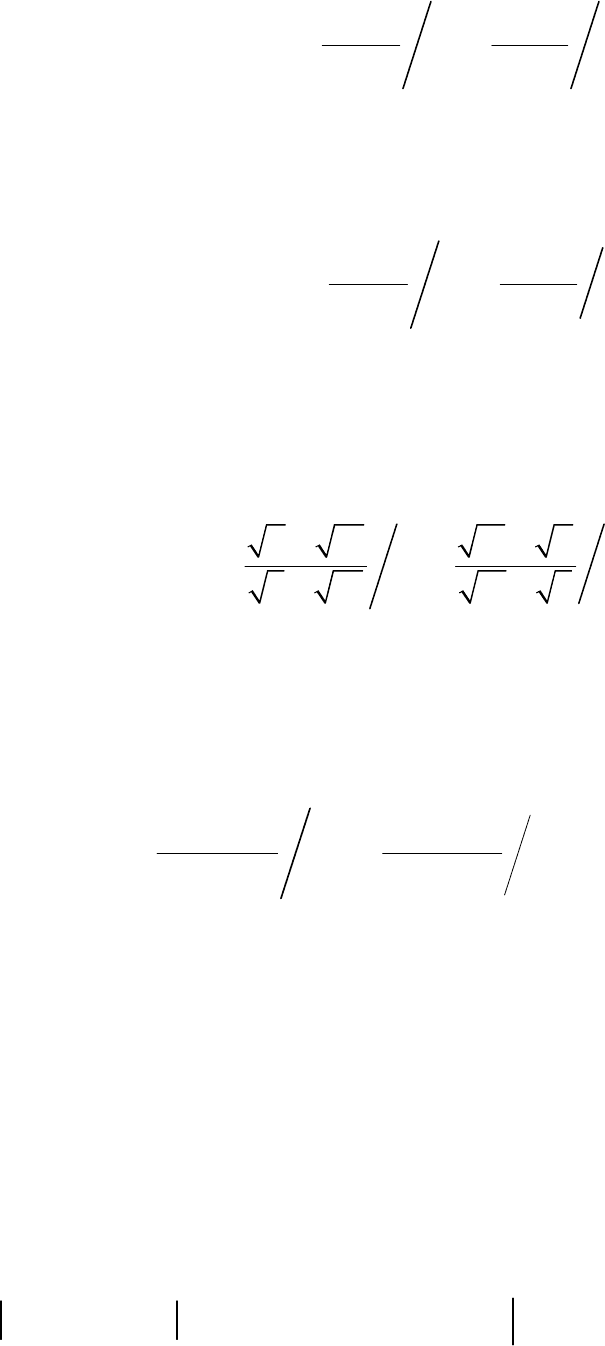
;
cb
ac
xa b x
A
Bx
ca b c
′′
′′
′′ ′′
−−
+= + =
′′ ′′
−−
∫∫
xc
(16)
б) вычитание нечетких чисел приводит к резу ьта
виде разности нечетких чисел:
л ту в
,
cb
a
xa b x
A
c
Bxxc
c b
′′
′
′′ ′′
−−
−= + =
′′
∫∫
,
a c
′′
−−
(17)
где
aab
′′ ′
=− bba
′
′′
=−
, cAB
=
− ;
в)
операция умножения нечетких чисел позволяет
опред с щ мелить произведение нечетких чи ел в следую е виде:
,
cb
xa b x
ac
A
Bxxc
′′
′′ ′′
−−
×= + =
∫∫
ca b c
′′
′′ ′′
−−
(18)
где ,aaa
′′ ′
=×
bbb
′
′′
=×
, ;
г)
деление нечетких чисел определяет частное от
нечетких чисел:
cAB=×
деления
() ()
:
() ()
cb
ac
xa b xc
A
Bx
cax b cx
′′
xc
′′ ′′
−−
′′
+=
′′ ′′
−−
, (19)
∫∫
=
где
:aaa
′′ ′
=
;
:bba
′
′′
=
;
ример 1.
:cAB= .
Выберем два нечетких числа
ПРИБЛИЗИТЕЛЬНО
П
66
=
жности
и ПРИБЛИЗИТЕЛЬНО с
функциями принадле :
88=
67
56
6(5)/ (7)/
x
xx=− +−
∫∫
x
.
ь перво ечеткое число
Пуст е «н 5
x
=
» имеет вид:
6
55
5
xx==
∫
6(5)55x= − =−=
0;
5,5
5, 5 : 6 5, 5
x=
5 0, 5;x ==−=
204
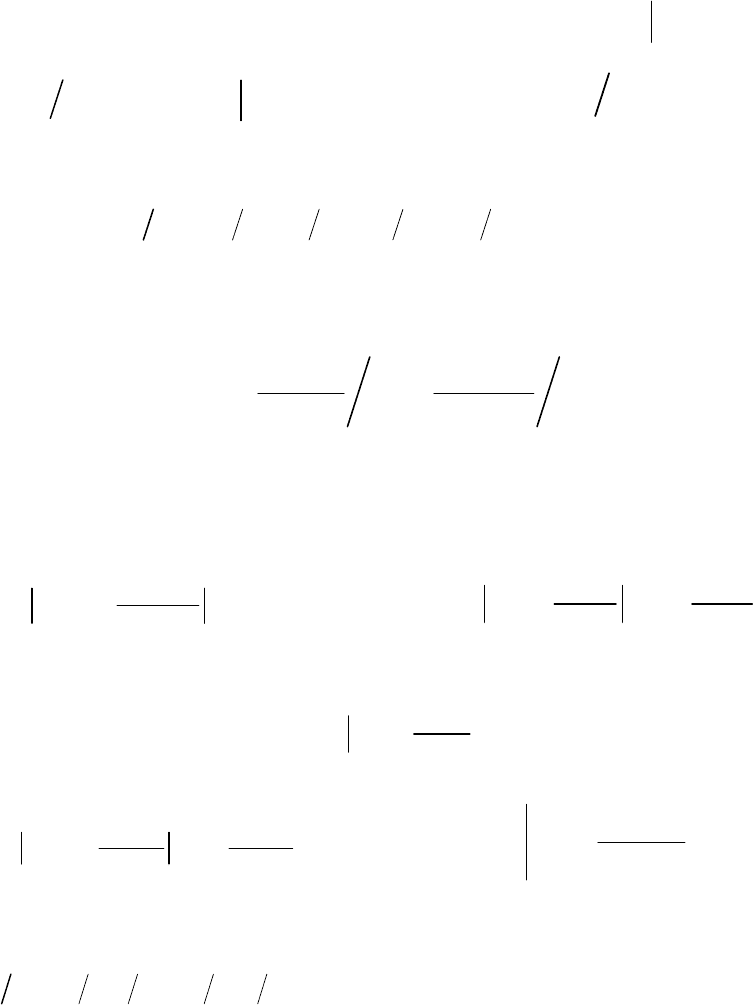
6x
=
Второе «нечеткое число » (значение подставляется
только в одно из слагаемых):
6
6651=
x=
=−
;
7
6,5 6,5
6
5 : 6 (7 ) 7 6,5 0,5;
xx==
=−=−=
∫
7
7:6 7 7 0
x
x
=
=
=−=
.
6,xx=
Итак, имеем следующее представление для «нечеткого
числа
{
6»:
}
6 0 5; 0,5=
5,5; 1 6; 0,5 6,5; 0 7
.
Аналогично для «нечеткого числа 8» имеем представление:
810
(6) (10)xx
66
8
86 108
x
x
−−
∫
−−
=+
∫
.
усть П
8
−
66
0
(6)
6:8 6 6 0;
86
xx
x
x
==
== =−
−
∫
=
77
676
7:8 0,5;
86 2
xx
x
x
==
−
−
== ==
−
8
86
8:8 1;
2
x
x
=
−
=
==
10
10 10
10 : 8
10
9
8
x=
9
8
10 10 9
9: 0,5;
22
x
x
x
=
−−
== ==
∫
0.
2
x
x
=
−
=
=
Итак, нечеткое числ 8» определяется соотношением:
=
« о
{
}
80 ;0=
с р я ачени м
е границы и вершин чисел: для
нечеткого числа значении нижней и верхней границ равны:
исл ения равны:
6;0,57;18;0,5910
.
В соответствии п ин тыми ранее обозн я и
определим верхние и нижни ы
6
5a =
6a
′
=
,
7b =
,
6A =
; для нечеткого ч а
8
эти знач
, ,
10b
′
=
8
B
=
.
Перейдем к выполнению арифметических операций над
нечеткими числами и .
6
8
205
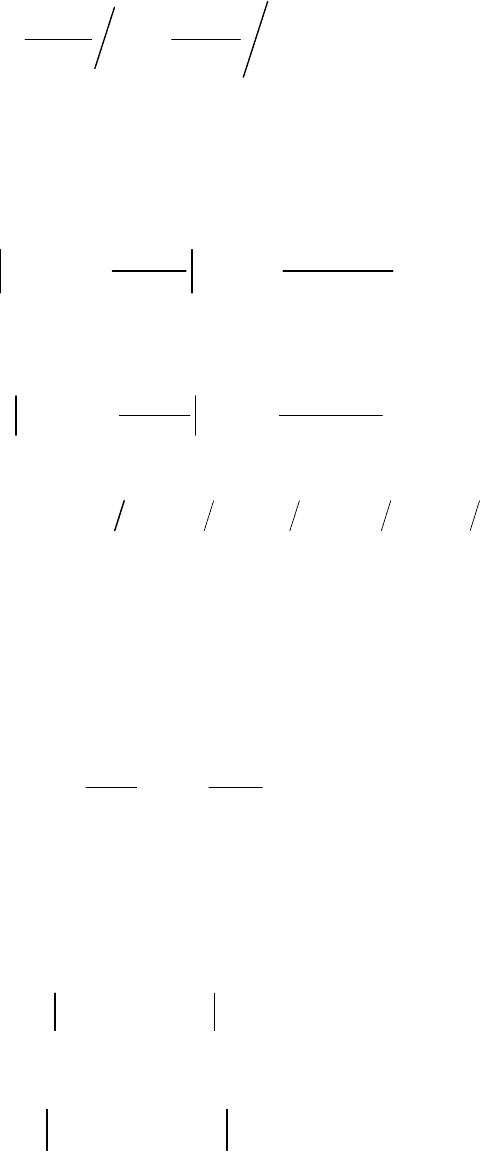
Сложение. Согласно формуле (15) найдем границу и
вершину результата, соответствующего сумме двух нечетких
чисел
6
и
8
:
5611;aaa
′
′′
=
+=+= 71017;bbb
′
′′
=
+=+ =
6814+=
. Тогда в
CAB=+=
соответствии с (16)
14 17
11 14
11 17
68 14
33
xx
xx
−−
+= + =
∫∫
.
Вычи
х точках:
слим значение функции принадлежности результата в
нескольки
12,5;x =
14
11 12,5 11x −−
12,5 12,5
11
14 0,5;
33
xx==
===
∫
15,5;x
=
17
15,5 15,5
14
17 17 15,5
14 0,5.
33
xx
x
==
−−
==
∫
=
Итак получен результат:
,
{
}
14 0 11; 0, 5 12,5; 1 14; 0,5 15,5; 0 17=
.
Вычитание. Значения границ и вершины результата
соответствующего разности нечетких чисел и равны:
; ;
,
8
86
6
651aaa
′′ ′
=−=−= 10 7 3bbb
′′ ′
=−= −=
2CBA
=
−= =− . Согласно
(17) результат вычитания имеет вид:
23
12
13
86 /
1
/ 2.
2 32
xx
xx
−−
−= + =
−
∫∫
нескольких точках
−
Значения функции принадлежности определяются в
следующими соотношениями:
при
1, 5x =
:
2
1,5 1,5
1
2(1)1,510,5;
xx
x
==
=− =−
∫
=
при
3
2,5 :
x
=
2,5 2,5
2
2(3)32,50,5.
xx
x
==
=− =−=
∫
206
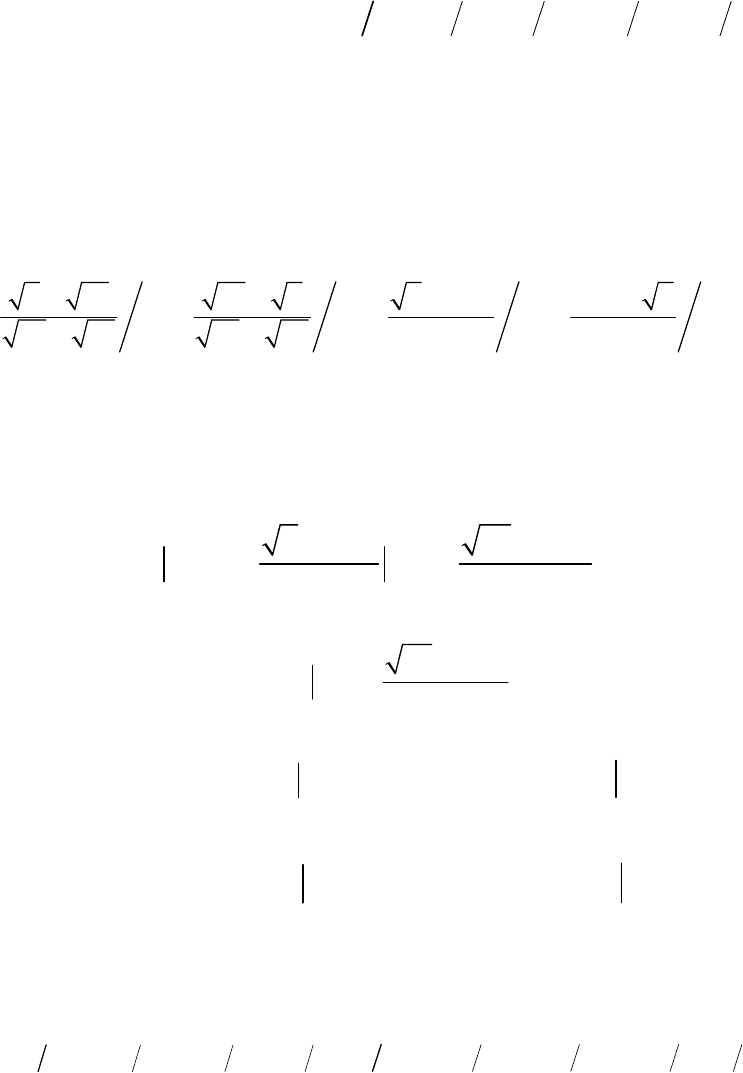
Т результат вычитания двух определенных выше чисел
огда
определится «величиной нечеткого числа и его функцией
принадлежност :
2
и» :
{
}
8 6 2 0 1; 0,5 1,5; 1 2; 0 5 2,5; 0 3−==
.
Умножение. Вычисл
,
им границы и вершину результата
умножения «нечетких чисел
6
и
8
» следующими
соотношениями:
56 30;aaa
′
′′
=
=⋅= 710 70;bbb
′
==⋅=
. Функция принадлежности произведения
′′
: 68 48CAB==⋅=
48 70 48 70
30 48 30 48
30 70 5,48 8,37
68 48.
1, 45 1, 44
48 30 70 48
xxxx
xxxx
−−−−
×= + = + =
−−
∫∫∫∫
Вычислим значение функции принадлежности в промежуточных
точках. Пусть
48
34 34
30
5, 48 34 5,48
48 0, 24.
1, 45 1,45
x==x
x −−
===
∫
чно: = 39:
Аналоги
X
39
39 5,48
48 0,53;
1, 45
x=
−
==
= 53:
X
53
48 0,76
X
= 44:
44
48 0,8;
x=
=
;
x=
=
X
= 58:
58
48 0,52;
=
=
X
= 64
x
:
64
48 0,26.
x=
=
Итак, результат произведения не
четких чисел и :
6
8
{
48 0 30; 0,24 34; 0,5=6 8 3 39; 0,8 44;×=
1 48; 0,76 53; 0,52 58; 0,26 64; 0 70
.
еление. Вычислим границы и вершину результата деления
«нече »
Функция принадлежности будет иметь следующий вид:
Д
ткого числа
8
» на «нечеткое число
6
:
:6:5 ;aaa
′′ ′
===
:10:71,43;bbb
′′ ′
== =
:8:61,33cBA===
.
1,2
207

1,33 1,43
1,2 1,33
1,33
( 1,2
1,43
1,2)1,33 (1,43 )1,33
8:6
(1, 33 1, 2) (1, 43 1, 33)
) 1,33 (1,43 ) 1,33
1, 33.
0,13 0,1
x(x
x
1,2 1,33
x
xx
x
xx
xx
−⋅
=+ =
−−
⋅ −⋅
=+ =
∫
∫∫
ри
ах определяются соотношениями:
−⋅
∫
x−
При этом значения функции п надлежности в
промежуточных точк
при
1, 24X =
:
1,33
1,24 24
( 1, 2) 1, 33 (1, 24 1, 2) 1, 33
1,33 0,39;
0,11 0,1 ,24
xx
x
x
==
−⋅ −⋅
===
1,
1,2
1 1⋅
∫
при
1, 28 :X =
1,28
1,33 0,76;
x=
=
X = 1,36:
1,36
1, 33 0
x=
= , 68;
при
1, 39 :X =
1,39
1,33 0,38.
x=
=
так, результат деления определяется соотношением: И
{
8 : 6 1, 33 0 1, 2; 0, 39 1, 24; 0, 76 1, 28;==
}
1 1,33; 0,68 1,39; 0,38 1,39; 0 1,43 .
Операции дополнительного вычитания и деления.
Введение основных арифметических операций обусловливает
расш сов математических моделей, где используются
нечеткие числа. Такими простейшими обобщенными моделями
являю е раические уравнения с нечеткими
числами моделей и операции над ними.
Во ногих задачах теории нечетких множеств возникает
необх четких ура ни
ирение клас
тся линейны алгеб
. Рассмотрим эти классы
м
одимость решения не вне й
A
XBD
+
=
, (20)
где
,,
A
BD
– нечеткие числа; – неизвестное. Найти решение
уравн
ля точного решения (в соответствующем смысле)
уравнения (20) введем операцию дополнительного вычитани
X
ения (20).
Д
я,
208

обознач
(21)
Решение уравнения (21), которое является множеством
аемую символом ( – –) и дополнительного деления - (//).
Определение 5. Пусть имеется уравнение с нечеткими
переменными:
XBD+=
.
X
DB=−
, будем определять операцией дополнительного
вычитания
(– –) (ОДВ).
Для решения уравнений необходимо изучить свойства ОДВ.
). Свойство носителя множества, определяемого ОДВ.
Пуст т л
1
ь носи ель множества
B
- интерва
12
[, ]
B
Sbb
=
, а носитель
множества
D −
интервал
12
[, ]
D
Sdd
=
. Тогда носитель
множества
, оп вид:
. (22)
2). Свойства функции принадлежности ОДВ. Функция
принадлежности множества задается соотношениями:
BXD=−
ределяемого ОДВ, имеет
12 12 1 12 2
[,] [,][ , ]
x
Sdd bb dbdb=−−=−−
X
,DB D
если ()
( ) inf sup( [0,1] min( ( ), ) ( )) inf 1,
если () ().
DD
xBD
z
zx
xa zxaz
z
xz
μμ
μμμ
μμ μ
−≤
⎧
=∈ −≤=
⎨
−≥
(23)
3). Условия определения ОДВ. Операция дополнительного
вычи л
⎩
тания определена только для нечетких чисе
D
и
B
, у
которых выполнены условия:
11 2 2
dbdb−≤ −
или
2121
,ddbb
−
≥−
(24)
т.е. длина интервала носителя уменьшаемого дол на быть
больше, чем у вычитаемого.
Определение 6. Пусть имеется уравнение
ж
A
XD
=
.
Операцией дополнительного деления (ОДД)
операц решение
называется
//
X
DA==
ия, которая определяет уравнения .
209

Свойства ОДД представляются соотношениями.
ойства носителя ОДД. Пусть носителем множеств 1). Св
A
и
D
являются соотв ственно интервалы:
12
[, ]
A
Saa
ет
=
и
12
[, ]
.
Тогда носитель множества, заданного ОДД, задается условиями:
D
Sdd=
112 2
:, : ,если 0, 0;
AD
dada S S>>
⎧
1221
12 12
21
:, :,если 0, 0;
[, ]//[, ]
:
сл
AD
x
dada S S
Sddaa
da
⎪
><
⎪
==
⎨
⎪
⎪
⎪
12
, :,если 0, 0;
AD
da S S
<
>
2211
:,:,е и 0, 0.
AD
dada S S<
⎪
⎪
⎪
<
⎩
2). Свойства функц
ии принадлежности ОДД. Функция
принадлежности множества X задается равенствами:
( ) inf sup [0,1] in( ( ,
1, ) ();
xA
t
D
m ( )
если (
inf
,если () ().
D
A
D
x
atxa
x t
μμ
μ
⎛⎞
=∈ ≥
⎜⎟
⎝⎠
<
⎧
⎪
(25)
()
t
DA
t
t
txt
μ
μ
μμ
=
=
≥
t
μ
⎨
⎪
⎩
3). Свойства носителей ОДД. Операция дополнительного
деления определена не для любых нечетких чисел
A
и .
Интервалы-носители чисел должны удовлетворять условиям:
1
, если
2
, если
уравнение
D
21 2
::dd aa>
0, 0;
AD
SS>>
21 1
::dd aa>
0, 0;
AD
SS><
(26)
12 21
::,dd aa>
если
0, 0;
AD
SS<>
::,dd aa>
если
SS<<
12 12
0, 0.
AD
XBD
+
=
Пример 2. Решить , где
B
= ПРИБЛИЗ 8 = {0 0 /9; 0/10}; ИТЕЛЬНО /6; 0,5/7; 1/8; ,5
= ПРИБЛИЗИТЕЛЬНО 14 = {0/10; 0,5/12; 1/14; 0,5/16; 0/18}.
D
210
