Козлов В.В. Надёжность горных машин и оборудования

Подождите немного. Документ загружается.

111

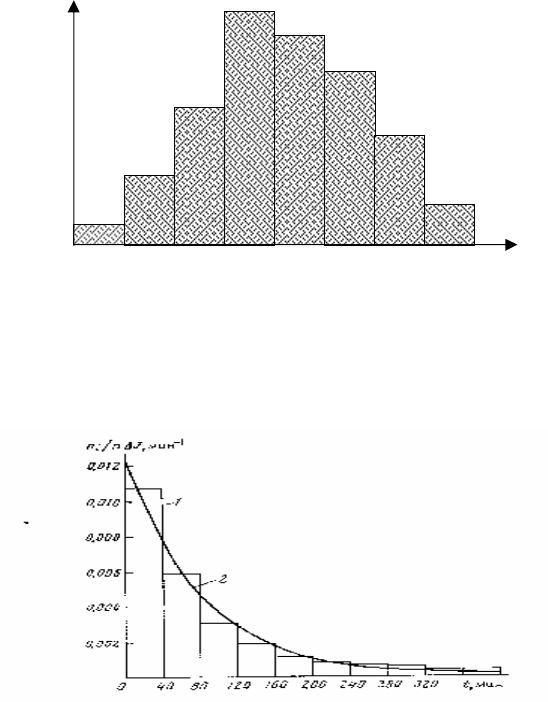
Рисунок 7.1 - Ступенчатая диаграмма эмпирической

плотности вероятности

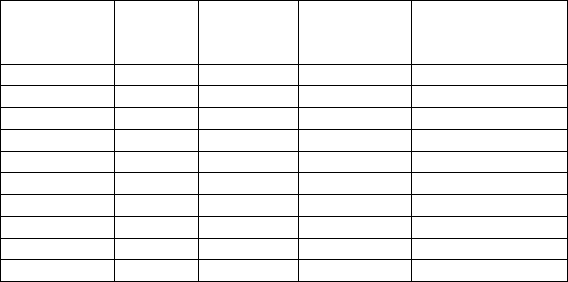
Рисунок 7.2 – Гистрограмма (1) и выравнивающая (2) экс-

поненциального распределения f(t)=0,0121е-

0,0121t случайных значений времени работы

между отказами очистного комбайна нового

комплекса

Если вид теоретической функции распределения СВ зара-

нее не известен, то внешний вид гистограммы может служить

основой для подбора той или иной теоретической дифференци-

альной функции распределения (плотности распределения), опи-

112

сывающей полученное эмпирическое распределение. Так, сопос-

тавив гистограмму (рис. 7.1) с теоретической кривой распределе-

ния (см. рис. 4.4) можно принять гипотезу о том, что СВ подчи-

няется нормальному закону распределения.

Сопоставив гистограмму, построенную по данным

табл. 7.2 (рис. 7.2), с графиком изменения вероятности безотказ-

ной работы объекта при экспоненциальном законе распределения

наработки между отказами или до отказа (см. рис.4.7 а), можно

предположить, что случайные значения времени t

, работы очист-

ного комбайнового комплекса между отказами подчиняются экс-

поненциальному закону распределения. Данное предположение

подкрепляется и тем фактом, что величина коэффициента вариа-

ции исследуемой СВ ν

=0,988,

т. е. весьма близка к единице, а

для экспоненциального закона распределения ν

= 1.

Таблица 7.3

Границы

интервалов

∆I, мин.

0,0121 t e

-0,0121t

f(t) =

= 0,0121е

0,0121t

0121,0

−

−=

eр

0 0 1,0 0,01210 -

40 0,485 0,6157 0,00745 0,3843

80 0,369 0,3795 0,00458 0,2362

120 1,453 0,2339 0,00282 0,1451

160 1,936 0,1443 0,00175 0,0896

200 2,420 0,0889 0,00107 0,0554

240 2,905 0,0547 0,0066 0,0342

280 3,390 0,0337 0,00041 0,02100

320 3,873 0,0208 0,00025 0,0129

400 4,840 0,0079 0,00010 0,0129

Плотность вероятности случайной величины, подчиненной

экспоненциальному закону распределения, описывается выраже-

нием

113

−

)(

Приняв в качестве математического ожидания его стати-

стическую оценку

= 83 мин, получим f(t) =0,0121 е

-0,0121t

Рассчитанные значения плотности вероятности на грани-

цах интервалов сведены в табл. 7.3.

На гистограмме (см. рис. 7.2) по данным табл. 7.З построе-

на выравнивающая кривая распределения, представляющая собой

график теоретической функции f(t), которая, сохраняя в основном

существенные особенности статистического распределения, сво-

бодна от случайных неправильностей хода гистограммы.

При подборе теоретической кривой распределения между

нею и статистическим распределением неизбежны некоторые

расхождения. При этом необходимо знать, объясняются эти рас-

хождения только случайными обстоятельствами, связанными с

ограниченным числом опытных данных, или они являются суще-

ственными и связаны с тем, что подобранная кривая плохо вы-

равнивает данное статистическое распределение.

Степень соответствия между выдвинутой гипотезой со

статистическим материалом устанавливается с помощью

критериев согласия.

Наиболее распространенным является критерий К. Пирсо-

на χ

, величина которого рассчитывается по формуле

∑

−

npn

)(

, (7.12)

где k - число интервалов группирования случайной величины;

114

- число значений случайной величины в i-ом интервале;

n- общее число полученных значений случайной величины;

- теоретическая вероятность попадания случайной величи-

ны в i-й интервал.

Теоретическая вероятность попадания случайной величи-

ны t в i-й интервал равна приращению функции распределения

на этом интервале:

).()()(

11 iiii

tFtFtttp −=<≤

Для экспоненциального закона распределения

,1)(

etF

−

−=

поэтому

eetttp

−−

−=<≤

)(

Значения p

приведены в табл.7.3. По формуле (7.12) и

данным табл. 7.2 и 7.3.

2,10

0129,0300

)0129,03008(

0129,0300

)0129,03006(

0210,0300

)0210,03007(

0342,0300

)0342,03009(

0554,0300

)0554,030014(

0896,0300

)0896,030022(

1451,0300

)1451,030036(

2362,0300

)2362,030070(

3843,0300

)3843,0300123(

222

⋅

⋅−

⋅

⋅−

⋅

⋅−

⋅

⋅−

⋅

⋅−

⋅

⋅−

⋅

⋅−

⋅

⋅−

⋅

⋅−

=χ

Число степеней свободы r распределения χ

определяется

по формуле

r = k – s,

115

где k - число интервалов группирования случайной величины;

s - число независимых условий (связей), наложенных на частоты

/n.

Такими связями является условие

∑

1, а также число l

неизвестных параметров теоретического распределения, опреде-

ляемых по данным выборки.

Условие

∑

1 - общее для различных законов распредле-

ния, следовательно, s =1 + l, и тогда r = k - l - 1.

'Так, например, для экспоненциального закона рас-

пределения

l = 1,













∑

;

для нормального закона распределения

l = 2,

иm













∑













=−

∑

)(χ

Пользуясь табл. 7.4, можно для полученных значений χ

числа степеней свободы r найти вероятность того, что величина,

распределенная по закону χ

превзойдет соответствующее значе-

ние.

Если получаемая вероятность р > 0,05 ÷ 0,1, то обычно

считается, что экспериментальные данные не противоречат

принятому теоретическому закону распределения случайной

величины.

116

Таблица 7.4

при p

0,9 0,8 0,7 0,5 0,3 0,2 0,1 0,05

2 0,211

0,446 0,713

1,386 2,41 3,22 4,6 5,99

3 0,584

1,005 1,424

2,37 3,66 4,64 6,25 7,82

4 1,064

1,649 2,21 3,36 4,88 5,99 7,78 9,49

5 1,611

2,34 3,0 4,35 6,06 7,29 9,24 11,07

6 2,2 3,07 3,83 5,35 7,23 8,56 10,64 12,59

7 2,83 3,82 4,67 6,35 8,38 9,80 12,02 14,07

8 3,49 4,59 5,53 7,34 9,52 11,03 13,36 15,51

9 4,17 5,38 6,39 8,34 10,66 12,24 14,68 16,92

10 4,86 6,18 7,27 9,34 11,78 13,44 15,99 18,31

В рассматриваемом примере χ

= 10,2; k=9. Для экспонен-

циального закона распределения случайной величины l = 1, по-

этому r = 9 – 1 – 1 = 7.

Согласно табл. 7.4 для χ

= 10,2 и г = 7, р > 0,1. Получен-

ная вероятность не является малой, поэтому гипотезу о том, что

случайные значения времени безотказной работы очистного

комбайнового комплекса распределены по экспоненциальному

закону, можно считать правдоподобной.

Таким образом, в результате обработки исходной стати-

стической информации о безотказности очистного комбайнового

комплекса, представленной в виде статистического ряда (см.

табл.7.2), установлены:

средняя наработка на отказ комплекса

117

.83

минmT

вид закона распределения непрерывной случайной вели-

чины t

0121,0

)(

−

;

аналитическое выражение для определения вероятности

безотказной работы комплекса

eetP

0121,0

)(

−

где t - текущая наработка комплекса с момента его включения.

Аналогичная статистическая обработка эксперименталь-

ных данных справедлива и при других законах распределения

непрерывных СВ. Так, например, при проверке гипотезы о соот-

ветствии экспериментального распределения СВ нормальному

закону распределения расчет значений плотности вероятности

f(t) на границах интервалов группирования случайной величины

и теоретической вероятности попадания СВ В I-е интервалы (см.

табл. 7.3) производится по формулам (З.15) и (3.16). При этом

необходимо помнить, что вероятность попадания случайной ве-

личины t в рассматриваемый интервал равна приращению функ-

ции распределения F(t) на этом интервале, т. е.

).()()(

1221

tFtFtttP −=<≤

118

Предварительно на основе статистического ряда, состав-

ленного по форме табл. 7.2, должны быть рассчитаны статисти-

ческие числовые характеристики

Dиm

Для расчетов асимметрии S

и эксцесса ε

(см. 3.1) распре-

деления по формуле (7.0) находятся статистические третий µ

четвертый µ

центральные моменты.

Если по характеру гистограммы можно принять гипотезу о

распределении СВ по логарифмически нормальному закону, то

на основе первичного статистического ряда (см. табл. 7.2) фор-

мируется статистический ряд для логарифмов СВ. По формулам

(7.9) и (7.10) находятся ,

Dиm где, например, τ - слу-

чайная величина времени восстановления работоспособного со-

стояния объекта.

Расчет значений f(τ) на границах интервалов и вероятно-

стей попадания СВ в i-е интервалы производится по формулам

плотности вероятности для логарифмически нормального рас-

пределения [см. 4.3].

При проверке согласованности эмпирического распреде-

ления СВ с теоретически нормальным или логарифмически нор-

мальным распределением с помощью критерия согласия χ

число

наложенных связей на частоты s=3, и поэтому число степеней

свободы распределения χ

рассчитывается как r = k – 3, где k -

число интервалов группирования СВ.

7.3 Доверительные границы показателей надежности

Формулы, приведенные в 1.2 позволяют получить точеч-

ные оценки показателей надежности. При известных законах рас-

пределения СВ, используемых для расчета показателей надежно-

сти, могут быть найдены интервальные оценки показателей

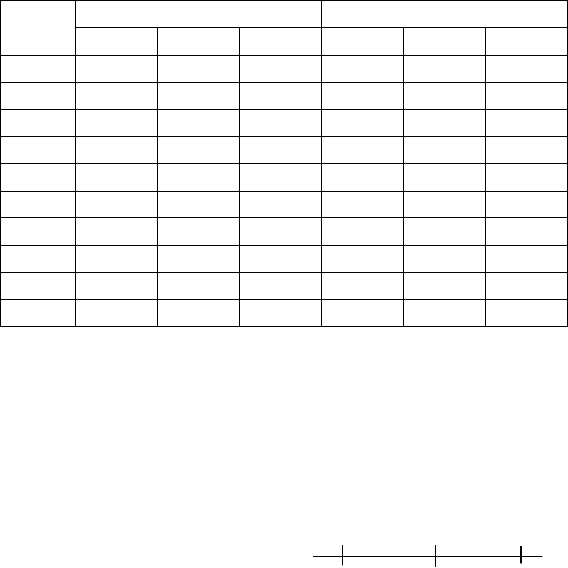
119

надежности.

Необходимость интервальных оценок обусловлена тем, что

и точечные оценки, полученные на основе выборочных данных,

содержат элемент случайности и являются приближенными. Ин-

тервальные оценки показателей надежности определяются уста-

новлением их верхней и нижней доверительных границ.

Таблица 7.5

γ = 0,8 γ = 0,9 γ = 0,95 γ = 0,8 γ = 0,9 γ = 0,95

10 1,37 1,61 1,83 0,73 0,65 0,59

15 1,28 1,46 1,62 0,78 0,70 0,65

20 1,24 1,37 1,51 0,81 0,74 0,69

25 1,21 1,33 1,44 0,83 0,76 0,72

30 1,18 1,29 1,39 0,84 0,78 0,74

40 1,16 1,24 1,32 0,87 0,81 0,77

50 1,14 1,21 1,28 0,88 0,83 0,79

100 1,09 1,14 1,19 0,91 0,88 0,85

200 1,06 1,10 1,13 0,94 0,91 0,89

300 1,05 1,08 1,10 0,95 0,93 0,91

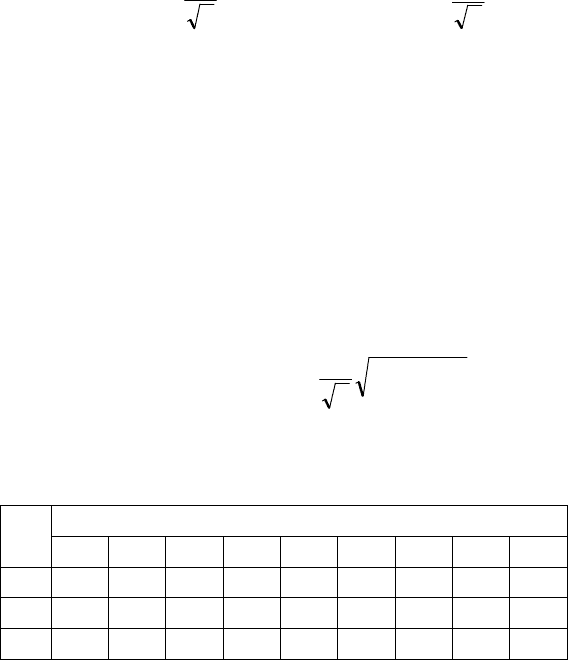
При экспоненциальном законе распределения случай-

ных величин времени работы оборудования между отказами и

времени восстановления границы интервальной оценки опреде-

ляются из выражений [4]:

верхней -

;

1010 в

TrТиTrT ==

120

нижней -

2020 в

TrТиTrT ==

где r

и r

- коэффициенты, определяемые в зависимости от объе-

ма данных п и принятой доверительной вероятности у (табл. 7.5).

При нормальном законе распределения случайных нарабо-

ток / между отказами доверительные границы для наработки на

отказ То определяются из выражений

;

tТТ

−=

где n - объем выборки (число полученных реализаций случайной

величины t для определения То);

- коэффициент Стьюдента, определяемый в зависимости от

принятой величины доверительной вероятности γ и вспомога-

тельной величины k = n - 1 (табл. 7.6);

Ot — среднее квадратическое отклонение случайной величины t.

Для логарифмически нормального закона распределения

случайных значений времени восстановления [4]:

,65,2115,1lg

γχ

σχ +++=

Таблица 7.6

при k

5 7 10 15 20 30 40 50 100

0,8 1,48 1,42 1,38 1,34 1,32 1,31 1,3 1,3 1,29

0,9 2,02 1,9 1,83 1,75 1,73 1,70 1,68 1,67 1,66

0,95

2,57 2,37 2,26 2,13 2,09 2,04 2,02 2,01 1,98