Кулешов А.А. Надежность горных машин и оборудования
Подождите немного. Документ загружается.


21
( )
dxex
F
ax
x
2
2
2
2
1
)(
σ
−
−
∞−
∫
πσ
=
.
Обозначая
σ
−
=
ax
Z
, получим
dzdx
dx
dz σ=
σ
= ;
, откуда
dzexF
z
x
2
2
2
1
)(
−
∞−
∫
π
=
.
Так как
5,0
2
1
2
0
2
=
π
−
∞−
∫
dze
z
, то
)(Ф5,0
2
1
5,0)(
2
0
2
ZdzexF
z
z
+=
π
+=
−
∫
,
где Ф(Z) – нечетная функция, т.е. Ф(–Z) = – Ф(Z).
Вероятность попадания случайной величины в заданный ин-
тервал [α, β] составит
Р[α < х < β] =
σ
−α
Φ−
σ
−β
Φ
aa
.
Пример. Наработка на отказ турбомуфты скребкового
конвейера распределяется нормально с параметрами а = 500 ч и
σ = 100 ч.
Определить вероятность безотказной работы для наработки
t
1
= 200 ч и t = 700 ч:
2
100
500700
;3
100
500200
21
=
−
=−=
−
= ZZ
;
Ф(–3) = –Ф(3) = –0,4987; Ф(2) = 0,4772;

22
Р(200) = 1 – F(200) = 1 – (0,5 – 0,4987) = 0,9987;
Р(700) = 1 – F(700) = 1 – (0,5 + 0,4772) = 0,0228.
Логарифмически-нормальное распределение наработки име-
ют многие невосстанавливаемые изделия, например, подшипники
качения. При таком распределении логарифм случайной величины х
распределен по нормальному закону.
Плотность вероятности:
( )
2
2
2
lglg
2
)(
σ
−
−
πσ
=
ax
e
x
M
xf
или
( )
2
2
2
lglg
2
1
)(
σ
−
−
πσ
=
ax
e
x
xf
,
где М = 0,43; σ – среднеквадратичное отклонение логарифма слу-
чайной величины.
Область возможных значений х лежит в интервале (0, +∞).
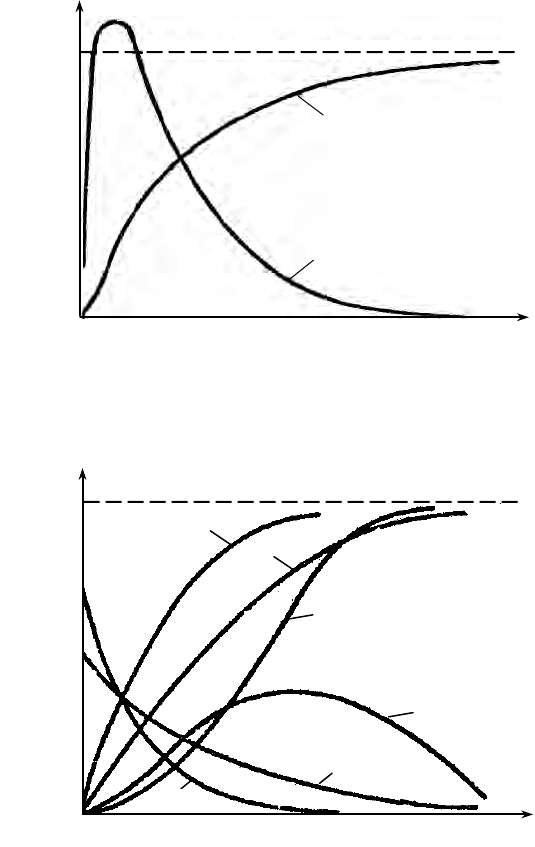
Математическое ожидание и дисперсия случайной величины х при
логарифмически-нормальном распределении (рис.1.3):
.1)(;)(
22
2
2
2
−==
σσ+
σ+
eexDexM
a
a
Распределение Вейбулла имеют некоторые объекты, у кото-
рых отказ наступает вследствие усталостного разрушения, многие
полупроводниковые приборы.
Распределение Вейбулла (рис.1.4) имеет функцию распре-
деления
b
a
x
x
exFexF
−
β
−
−=−= 1)(;1)(
2
и плотность вероятности
23
Рис.1.3. Логарифмически-нормальное распределение
случайной величины
Рис.1.4. Распределение Вейбулла
F
(
x
),
f
(
x
)
1
F(x)
f (x)
0
х
f (a)
х
0
F(x), f(x)
1
b < 1, F(x)
1, F(x)
> 1,
F
(
x
)
1, f (x)
> 1, f (x)
< 1, f (x)

24
.)(;)()(
1
1
2
b
a
x
b
x
d
e
a
x
a
b
xfexxFxf
−
−
β
−
−
=
β
α
==
Параметр α оказывает влияние на вид функции распределе-
ния и плотность вероятности.
Экспоненциальное распределение. Распределение Вейбулла
при b = 1 имеет плотность вероятности
a
x
e
a
xf
−
=
1
)(
и функцию распределения
a
x
exF
−
−= 1)(
.
Это распределение называется экспоненциальным и имеет
особое значение в теории надежности.
Наработка на отказ многих невосстанавливаемых изделий
(средств автоматизации и радиоэлектронной аппаратуры и др.), у
которых явление износа и старения слабо выражены, распределены
экспоненциально.
Вероятность безотказной работы
a
t
etFtP
−
=−= )(1)(
.
Интенсивность отказов
const
1
)( ==λ
a
t
.
Поэтому плотность вероятности и функцию распределения
при экспоненциальном распределении записывают в виде
t
etf
λ−
λ=)(
.
Функция распределения
t
etF
λ−
−= 1)(
.

25
Размерность λ[с
–1
] – количество отказов в единицу времени.
Можно показать, что средняя наработка до отказа
λ= /1
0
T
и
дисперсия
2
/1 λ=D
.
Пример. Интенсивность отказов гидронасоса комбайна
λ = 0,0006 ч
–1
. Определить вероятность безотказной работы насоса
за 300 ч и среднюю наработку до отказа.
Вероятность безотказной работы за 300 ч
835,0)(1)(
18,03000006,0
===−=
−⋅−
eetFtP
.
Средняя наработка до отказа
1667
0006,0
11
0
==
λ
=T
ч.
Вероятность безотказной работы при этом распределении за-
висит только от длины рассматриваемого интервала времени ∆t и не
зависит от момента времени τ, с которого начинается отсчет.
Гамма-распределение. Если устройство состоит из одного
рабочего и n резервных элементов, каждый из которых включается в
работу после отказа предыдущего, то отказ устройства наступит в
тот момент, когда выйдет из строя элемент n + 1.
Если все элементы имеют экспоненциальное распределение
с интенсивностью отказов λ, то наработка до отказа всего устройст-
ва будет иметь γ-распределение с параметрами λ и m = n + 1.
Плотность распределения случайной величины (рис.1.5) оп-
ределяется из выражения
( )
tmm
et
m
tf
л1
Г
1
)(
−−
λ=
,
где Г – обозначение γ-функции, если m – целое число, то Г(m) =
= (m – 1)!
Гамма-распределение наработки и времени восстановления
могут иметь некоторые другие объекты, в этом случае m может быть
как целым, так и дробным числом.

26
При m = 1 γ-распределение имеет плотность вероятности
t
etf
л
л)(
−
=
,
т.е. экспоненциальное распределение является частным случаем
γ-распределения.
Математическое ожидание и дисперсия случайной величины,
имеющей γ-распределение:
.)(;)(
2
λ
=
λ
=
m
tD
m
tM
Усеченное нормальное распределение. Часто целесообразно
использовать такие распределения, полученные путем ограничения
интервала возможного значения случайной величины θ (рис.1.6).
Минимальная наработка S > 0, максимальная S < r. Интервал
наработки [S, r]. Случайное значение t
в
также заключено в некото-
ром интервале.
Если исходное распределение имеет плотность вероятности
f
1
(t), а усеченное – плотность вероятности f
2
(t), то f
2
(t) = с
f
1
(t).
Рис.1.5. Гамма-распределение
t
0
f
(
x
)
m > 2
1 < m < 2
0 <
m
< 1
m = 1

27
Рис.1.6. Усеченное нормальное распределение
Так как при любом интервале изменения случайной величи-
ны
1)(
2
=
∫
dttf
r
S
, то постоянная с может быть определена из условия
[ ]
1)()()(
121
=−=
∫
SFrFcdttfс
r
S
,
откуда
)()(
1
11
SFrF
c
−
=
,
где F
1
(r), F
1
(S) – значения исходной функции в точках, соответст-
вующих r и S.
Для нормального распределения
( ) ( )
12
ФФ
1
ZZ
c
−
=
,
где
σ
−
=
σ
−
=
aS
Z
ar
Z
12
;
.
t
0
f
2
(t)
f
1
(t)
f
(t)
s r

28
При интервале [0, ∞] изменения случайной величины
σ
−=∞=
a
ZZ
12
;
.
Соответственно
Ф(Z
2
) = 0,5; Ф(Z
1
) = –Ф
σ
a
;
σ
+
=
а
c
Ф5,0
1
.
Пример. Интенсивность отказов гидронасоса комбайна
λ = 0,0006 ч
–1
. Определить вероятность безотказной работы насоса
за 300 ч и среднюю наработку до отказа.
Вероятность безотказной работы за 300 ч
835,0)(1)(
18,03000006,0
===−=
−⋅−
eetFtP
.
Средняя наработка до отказа
1667
0006,0
11
0
==
λ
=T
ч.
1.4. ПОКАЗАТЕЛИ НАДЕЖНОСТИ
Для решения практических вопросов в области надежности
используются показатели, с помощью которых характеризуется ко-
личественно уровень надежности горных машин и оборудования.
Показатели надежности позволяют:
• оценивать надежность машин при проектировании, опре-
делять ее экспериментально при испытании и эксплуатации машин;
• оценивать влияние уровня надежности машин на произ-
водительность Q;
• намечать пути повышения надежности, применяемого и
вновь создаваемого оборудования;
• рассчитывать количество запчастей;

29
• определять оптимальную периодичность профилактики
горных машин.
Для количественной характеристики надежности могут ис-
пользоваться различные показатели, которые относятся к различным
свойствам надежности.
1.4.1. Показатели безотказности
Безотказность – вероятность того, что в пределах заданной
наработки отказа объекта не возникнет.
Показатели безотказности невосстанавливаемых объектов:
• вероятность безотказной работы Р(t
0
) – вероятность то-
го, что в пределах заданной наработки отказ объекта не возникнет;
• интенсивность отказов λ(t) – условная плотность воз-
никновения отказа, определяемая для рассматриваемого момента
времени при условии, что до этого отказ не возник;
• средняя наработка до отказа T
0
– математическое ожи-
дание наработки до первого отказа.
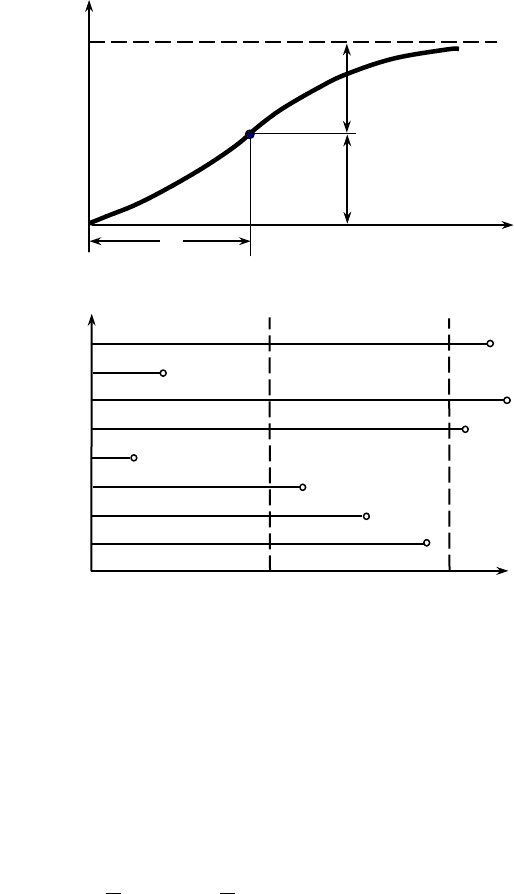
Математическое определение вероятности безотказной ра-
боты от начала эксплуатации до t
0
(рис.1.7):
• вероятностное
{ }
)(1),0()(
0000
tFtPtPtP −=≥θ==
,
где
θ
– случайное время работы (наработки) объекта до отказа
(между отказами);
)
(
0
tF
– функция распределения случайной ве-
личины
θ
;
• статистическое
)0(
)(
1
)0(
)()0(
)0(
)(
)(
€
000
0
N
tn
N
tnN
N
tN
tP −=
−
==
,
где
)(
0
tN
– количество исправленных объектов в момент време-
ни t
0
;
)0(N
– количество исправленных объектов в момент времени
t = 0;
)(
0
tn
– количество отказов объектов за время t
0
.
30
Рис.1.7. Определение безотказности: а – вероятностное;
б – статистическое
Таким образом,
)(
€
0
tP
– отношение числа объектов, безот-
казно проработавших до момента времени t
0
, к числу объектов, ис-
правленных в начальный момент времени t = 0, или частость собы-
тия, состоящего в том, что реализация времени работы объекта до
отказа окажется больше заданного времени работы t
0
.
Рассмотрим это на примере:
7
3
)(
€
0
=tP
;
7
2
)(
€
1
0
=tP
или
43,0)(
€
0
=tP
;
29,0)(
€
1
0
=tP
;
t
0
F
(
t
0
) =
Q
(
t
0
)
F
(t)
a
1
0
P(t
0
) = f – F(t
0
)
t
Номер
объекта
б
8
7
6
5
4
3
2
1
t
0
t
0
t
′
