Куликовский П.Г. Справочник любителя астрономии

Подождите немного. Документ загружается.

§ 3.4. Движение Луны. Затмения

261

будут наблюдаться вновь примерно в тех же местах Земли. Этот период, называемый

саросом (по-халдейски — «повторение»), содержит в себе

19 драконических годов по 346,620063

= 6585,780589 солнечных суток,

223 синодических месяца rio 29,530588

= 6585,321146 солнечных суток,

242 драконических месяца по 27,2l2220

= 6585,357240 солнечных суток,

239 аномалистических месяцев по 27,554550

= 6585,537570 солнечных суток,

18 аномалистических годов по 365,25964134

= 6574,673543 солнечных суток.

За это время произойдет в среднем 84 затмения (от 78 до 94): 43 солнечных

(от 39 до 48) и 28 лунных (от 25 до 30). Эпохи наибольшего и наименьшего

числа затмений в саросе повторяются в среднем через 290 лет. Однако так как

223 синодических месяца не в точности составляют 242 драконических (разность

между ними 0,04 суток), то обстоятельства затмений не будут повторяться в точности

и полосы затмений будут смещаться по поверхности Земли. Кроме того, поскольку

в саросе не целое число суток, за 0,3 суток Земли повернется еще на ~ 120°.

В габл. 24 приведены солнечные затмения, которые произойдут до 2040 г.,

а в табл. 20 — лунные затмения за тот же период.

262 Глава 3. Краткие сведения из общей астрономии

§ 3.5. Движение планет и комет

Видимые движения планет среди звезд зодиакальных созвездий имеют характерные

особенности (петли и точки возврата), которые были известны уже древним: прямое

движение планеты навстречу суточному движению небесного свода сменяется после

кажущегося «стояния» попятным движением, после чего вновь продолжается пря-

мое движение (рис. 184). Дуга попятного движения меньше у планет, находящихся

0° Ж° 240° !вО° 720° О'

97X7°

24/7° 7вО° 720° 6/7° /7° ЗЯ7° 240°

*720'

о'о'

Рис. 184. Движение Венеры и Солнца в

932-1 933 гг. Показано положение

Солнца первого числа указанных месяцев. Движение Сатурна в

929-1 930 гг.

Положение Солнца лишь вблизи начала каждого года

1 1 1 1

Сатур»

27. Ob

1 1 Т 1

'79. Об

mi/)

1 1 1 1

Сатур»

27. Ob

09.0'/

79SO.O

___^>29.0В

193Ю 01.07

>09.09

05.07.7931 Змлиптима г5.72.

7929

,.>1111 —1_

74. 72.7926

Г— , , -о-

~2вР ~2вГ ~27<Г ~27Г° ~27f° ~273° ~2тГ° 269° 267° 265° 269°

дальше от Земли. По положению своих орбит относительно орбиты Земли планеты

делятся на нижние (или внутренние) и верхние (или внешние). Нижние плане-

ты — это те, орбиты которых находятся внутри орбиты Земли: Венера и Меркурий.

Верхние — все остальные.

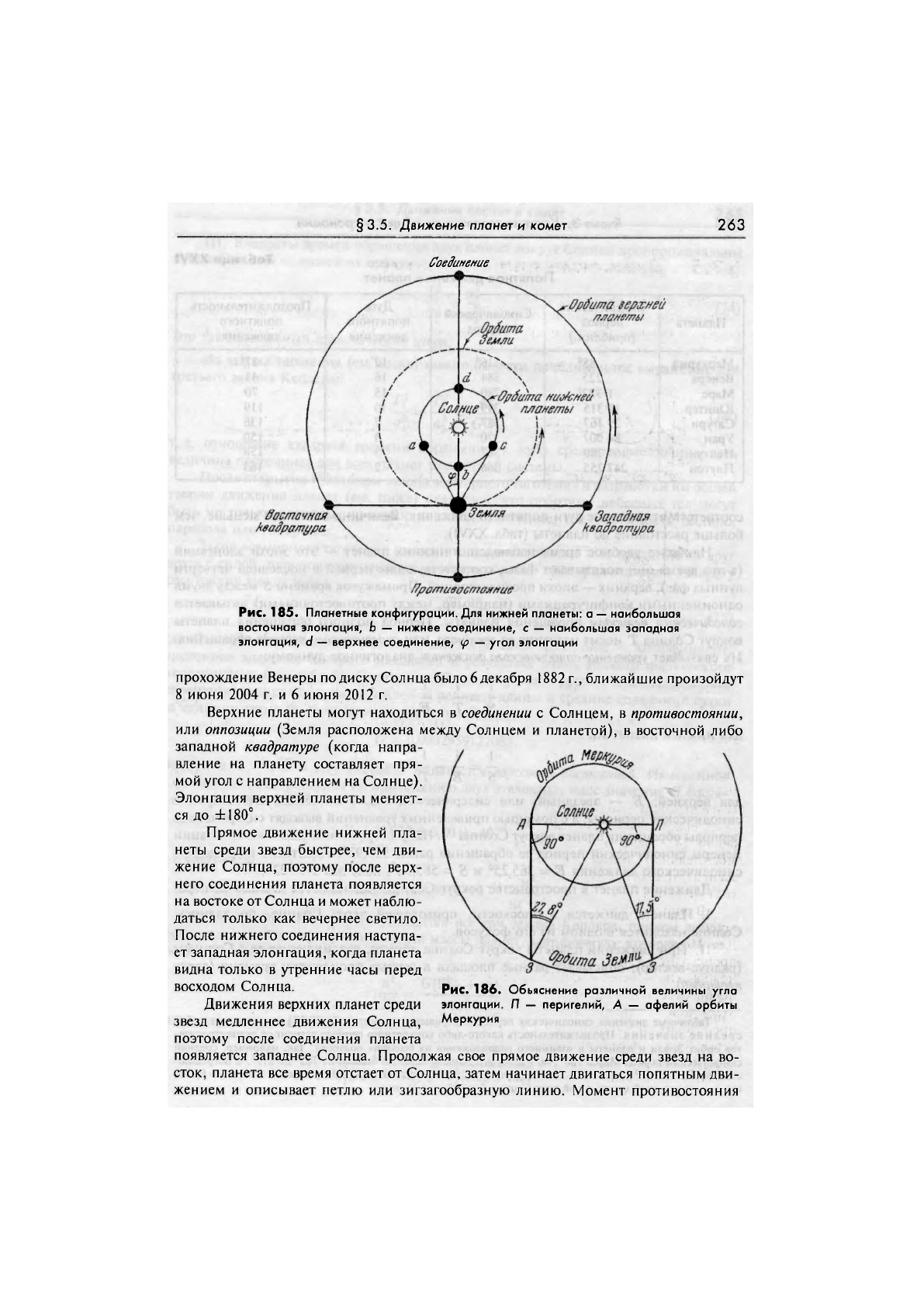
По видимому положению относительно Солнца нижние планеты могут образо-

вывать следующие конфигурации (рис. 185): нижнее соединение (планета расположена

между Солнцем и Землей, разность геоцентрических долгот равна 0°), верхнее соеди-

нение (планета находится за Солнцем)

>, западную или восточную элонгацию (плане-

та на некотором угловом расстоянии от Солнца). Наибольшая элонгация Меркурия

около 28°, Венеры около 48°. Как легко можно понять из рис. 186, вследствие

значительного эксцентриситета орбиты Меркурия угол его наибольшей элонгации

зависит от взаимного расположения его орбиты и Земли в момент элонгации. Этот

угол меняется от 17°30' до 27°45'.

В эпохи нижних соединений, если планета близка к какому-нибудь узлу своей

орбиты, может наблюдатьф редкое явление — прохождение планеты по диску Солнца.

Для Меркурия это происходит в мае или ноябре раз в несколько лет: за 217 лет

происходит 9 майских и 20 ноябрьских прохождений — майские через 13 или 33 года,

ноябрьские — через 7 или 13 лет; после каждого майского через 3,5 года происходит

ноябрьское прохождение Меркурия по диску Солнца. Ближлишие прохождения

Меркурия по диску Солнца: 7 мая 2003 г. и 8 ноября 2006 г. Для Венеры это

происходит значительно реже и в следующей последовательности: через 121,5 года,

через 8 лет, через 105,5 года, через 8 лет, через 121,5 года и т.д. Последнее

* Понятие «соединение» применяется и к любым другим двум светилам, но в этом случае должна

быть равна нулю разность прямых восхождений, а не долгот.

§ 3.5. Движение планет и комет

263

Соединение

Рис. 185. Планетные конфигурации. Для нижней планеты: а — наибольшая

восточная элонгация, Ь — нижнее соединение, с — наибольшая западная

элонгация, d — верхнее соединение, ip — угол элонгации

прохождение Венеры по диску Солнца было 6 декабря 1882 г., ближайшие произойдут

8 июня 2004 г. и 6 июня 2012 г.

Верхние планеты могут находиться в соединении с Солнцем, в противостоянии,

или оппозиции (Земля расположена между Солнцем и планетой), в восточной либо

западной квадратуре (когда напра-

вление на планету составляет пря-

мой угол с направлением на Солнце).

Элонгация верхней планеты меняет-

ся до ±180°.

Прямое движение нижней пла-

неты среди звезд быстрее, чем дви-

жение Солнца, поэтому после верх-

него соединения планета появляется

на востоке от Солнца и может наблю-

даться только как вечернее светило.

После нижнего соединения наступа-

ет западная элонгация, когда планета

видна только в утренние часы перед

восходом Солнца.

Движения верхних планет среди

звезд медленнее движения Солнца,

поэтому после соединения планета

появляется западнее Солнца. Продолжая свое прямое движение среди звезд на во-

сток, планета все время отстает от Солнца, затем начинает двигаться попятным дви-

жением и описывает петлю или зигзагообразную линию. Момент противостояния

Рис. 186. Обьяснение различной величины угла

элонгации. П — перигелий, А — афелий орбиты

Меркурия

264

Глава 3. Краткие сведения из общей астрономии

Таблица XXVI

Попятное движение планет

Планета

Сидерический

период

(приближ.)

Синодический

период

Дуга

попятного

движения

Продолжительность

попятного

движения

Меркурий 88"

116

12° 17"

Венера 225

584

16 41

Марс

322

780

15 70

Юпитер

11 315

399

119

Сатурн

29 167

387 7 136

Уран

84 007 370

4 150

Нептун

164 280

367 3

158

Плутон 247 255

366 2 163

соответствует середине дуги попятного движения. Величина петли тем меньше, чем

больше расстояние до планеты (табл. XXVI).

Наиболее удобное время наблюдения нижних планет — это эпохи элонгации

(в это время они показывают фазы, соответствующие первой и последней четверти

лунных фаз), верхних — эпохи противостояний. Промежуток времени S между двумя

одноименными конфигурациями (например, между противостояниями) называется

синодическим периодом обращения планеты. Период полного обращения планеты

вокруг Солнца Т носит название ее звездного, или сидерического периода обращения.

Их связывает уравнение синодического движения, аналогичное лунному:

1 = 1-1 (72)

S Т Е

для нижней планеты и

111

- = (73)

SET

для верхней: Е — звездный, или сидерический год. Из наблюдений получают

синодические периоды, а с помощью приведенных уравнений выводят сидерические

периоды обращения планет вокруг Солнца

Например, по наблюдениям элонгации

Венеры синодический период ее обращения равен 583,92

. Подставив в уравнение

синодического движения Е

—

365,25

и S = 583,92

, получим Т = 224,7

Движение планет в пространстве вокруг Солнца подчиняются законам Кеплера:

I. Планета движется в плоскости, проходящей через Солнце, по эллипсу,

Солнце находится в одном из его фокусов.

II. При движении планеты вокруг Солнца прямая, соединяющая ее с Солнцем

(радиус-вектор), описывает равные площади в равные промежутки времени (закон

площадей).

"'Табличные значения синодических периодов обращения планет (табл. XXVI) представляют собой

средние значения. Продолжительность какого-либо конкретного периода зависит от эксцентрисите-

тов орбит Земли и планеты и взаимного расположения их больших полуосей. Так, например, средний

синодический период Марса 780

, но в действительности периоды бывают от 765

до 81 I

. С погрешно-

стью не больше I0

, а большей частью меньше 5

, синодический период Марса равен S = 811 — 0,27х,

где I — число дней между датой оппозиции и ближайшим 16 июля.

§3.5. Движение планет и комет

265

III. Квадраты времен обращения двух планет вокруг Солнца пропорциональны

кубам больших полуосей их орбит:

(74)

Это так называемый гармонический закон.

Из закона тяготения (см. ниже) можно вывести приближенное выражение для

третьего закона Кеплера:

£ = 2 J

Gm@ '

т. е. отношение квадрата времени обращения к кубу среднего расстояния есть

величина постоянная для всех планет Солнечной системы.

После открытия Ньютоном закона всемирного тяготения и разработки им общей

теории движения планет (см. ниже) оказалось, что орбитами небесных тел могут

быть не только эллипсы, но любое коническое сечение, т.е. окружность, эллипс,

парабола или гипербола.

Закон всемирного тяготения гласит, что все космические тела притягивают друг

друга с силой, пропорциональной их массам и обратно пропорциональной квадрату

расстояния между ними:

F = G-V

, 75

где G — гравитационная постоянная, или постоянная тяготения — коэффициент,

численное значение которого находится в результате очень тонкого физического

эксперимента (см. табл. 5). Если массу Солнца принять равной единице, среднее

расстояние между Солнцем и Землей за единицу длины и средние солнечные сутки

за единицу времени, то численное значение G будет

G = 0,0002959122083.

Величина к —

Vg = 0,01720209895 называется гауссовой постоянной. Измеренное

в физических лабораториях по притяжению двух эталонных масс значение G соста-

вляет в системе CGS

—

(6,672 ± 0,001)

•

10~

и в системе SI

G= (6,672 ±0,001)- Ю

-11

см

Из закона Ньютона строго выводятся все три закона Кеплера, причем вывод

третьего закона Кеплера, учитывающий массы планет, дает формулу, которая ближе

соответствует действительности:

G(9Jl® + т)

4тг

или, в случае сравнения двух планет,

(76)

266 Глава 3. Краткие сведения из общей астрономии

Здесь ЯЛ© — масса центрального тела (например, Солнца), a a

Ш| и а

, тп

—

соответственно большие полуоси орбит и массы двух тел, обращающихся вокруг

центрального.

Эту формулу можно применить к любым двум телам Солнечной системы,

из которых одно обращается вокруг другого, и использовать ее для определения масс

планет, имеющих спутники.

Применяя эту формулу к движению Земли вокруг Солнца (Т| =

год, а\ =

а. е.)

и к движению Луны вокруг Земли (Т

= 0,0748 года, а

— 0,00257 а. е.), можно

составить соотношение

Пренебрегая в числителе массой Земли, малой по сравнению с массой Солнца,

а в знаменателе массой Луны, малой по сравнению с массой Земли, получим

Зная из лабораторных измерений значение G

—

6,672

•

-11

•

/кг

и ускорения

свободного падения g = Gm^/R®

= 9,81 м/с

, а из геодезических измерений —

радиус Земли Я® = 6378 км, найдем массу Земли: то® = 5,98 • 10

кг. Тогда

отношение (77') даст нам и массу Солнца = 2,0

•

кг.

Применяя эти рассуждения к другой планете с массой тп

, имеющей спутник,

можно определить отношение Ш

/т

и, зная Ш1®, вычислить т

. Массу планеты,

не. имеющей спутников, можно определить лишь из анализа тех возмущений,

которые эта планета вызывает в движении других планет, комет или пролетающих

мимо нее космических аппаратов. Об определении массы Луны см. п. 1.1.1.

Применяя формулу (76) к двойным звездам, либо к двойным галактикам, мы

можем получить оценку суммы масс звезд или галактик (п. 1.10.10).

Изучение движения планеты вокруг Солнца в небесной механике носит на-

звание задачи двух тел. В общем виде эту задачу можно сформулировать так:

два сферических тела (однородные или со сферично-симметричным распределением

плотности) с известными массами находятся под действием взаимного тяготения; да-

ны их положения и скорости относительно какой-то системы координат в некоторый

момент; каковы будут их расположение и скорости в любой последующий (или были

в любой предыдущий!) момент времени? Иначе говоря, каково будет их движение?

Ньютон показал, что возможные орбиты в задаче двух тел — это конические

сечения; движение происходит под действием центральной силы и подчиняется

законам Кеплера.

При движении по эллиптической орбите максимальная линейная ско-

рость (Vmax) достигается в точке перицентра (при ближайшем расположении тел),

а минимальная скорость (F

) — в точке апоцентра (при наиболее удаленном

расположении). Если одно из тел значительно массивнее другого (М > то), то для

меньшего тела эти скорости составляют

9Л®

+ то® I

(77)

то® + Шц ' (0,0748)

(0,00257)

Ше

то®

330 000.

(77')

(78)

§ 3.5. Движение планет и комет

267

где а — большая полуось эллипса, е — его эксцентриситет, г

и г

— расстояния

в апоцентре и перицентре. Средняя скорость (F) достигается на концах малой оси

эллипса:

В любой точке эллиптической орбиты на расстоянии г от массивного тела

скорость малого тела составляет

На круговой орбите (е = 0, г = а) скорость постоянна; это круговая ркорость:

Если для Миг принять значения массы и радиуса космического тела, например,

планеты, то получим первую космическую скорость для этой планеты (V|). Так, для

Земли V\ = л/СМ

/Д

= 7,9 км/с.

На параболической орбите (е = 1, а = оо) в любой ее точке тело движется

с параболической скоростью:

значение скорости зависит от текущего расстояния. Вычисленная для поверхности

планеты (или звезды), эта скорость называется второй космической скоростью (Vj|),

а также скоростью убегания, ухода, освобождения, ускользания или критической

скоростью. У поверхности Земли Ум = 11,2 км/с.

Рис. 187 дает пример зависимости формы и расположения орбиты одного тела

вокруг другого, принимаемого за неподвижное, от различия в величине (а) или

(79)

Рис. 187. Орбиты, образующиеся при различных скоростях в точке А,

направленных в одну и ту же сторону (а); эллиптические орбиты при

различных направлениях равных скоростей в точке А (б)

268

Глава 3. Краткие сведения из общей астрономии

направления (б) скорости в точке А. Так, например, если на расстоянии 1 а. е.

от Солнца тело имеет скорость меньше 42 км/с, то орбита будет эллиптической,

больше 42 км/с — гиперболической. Скорость 42 км/с называется параболической

(для этого расстояния), а в космонавтике — третьей космической.

Вычисление движения двух тел представляет относительно простую задачу.

Пусть теперь даны массы, взаимные расстояния и скорости трех тел в некоторый

момент и требуется вычислить их расстояния и скорости в последующие (или преды-

дущие) моменты времени. Эта «задача трех тел» исключительно сложна. Общего

решения ее, годного для практического применения, до сих пор еще не найдено.

Только в некоторых частных случаях, например, когда тела движутся в одной плоско-

сти и массой одного из них можно пренебречь по сравнению с массами двух других,

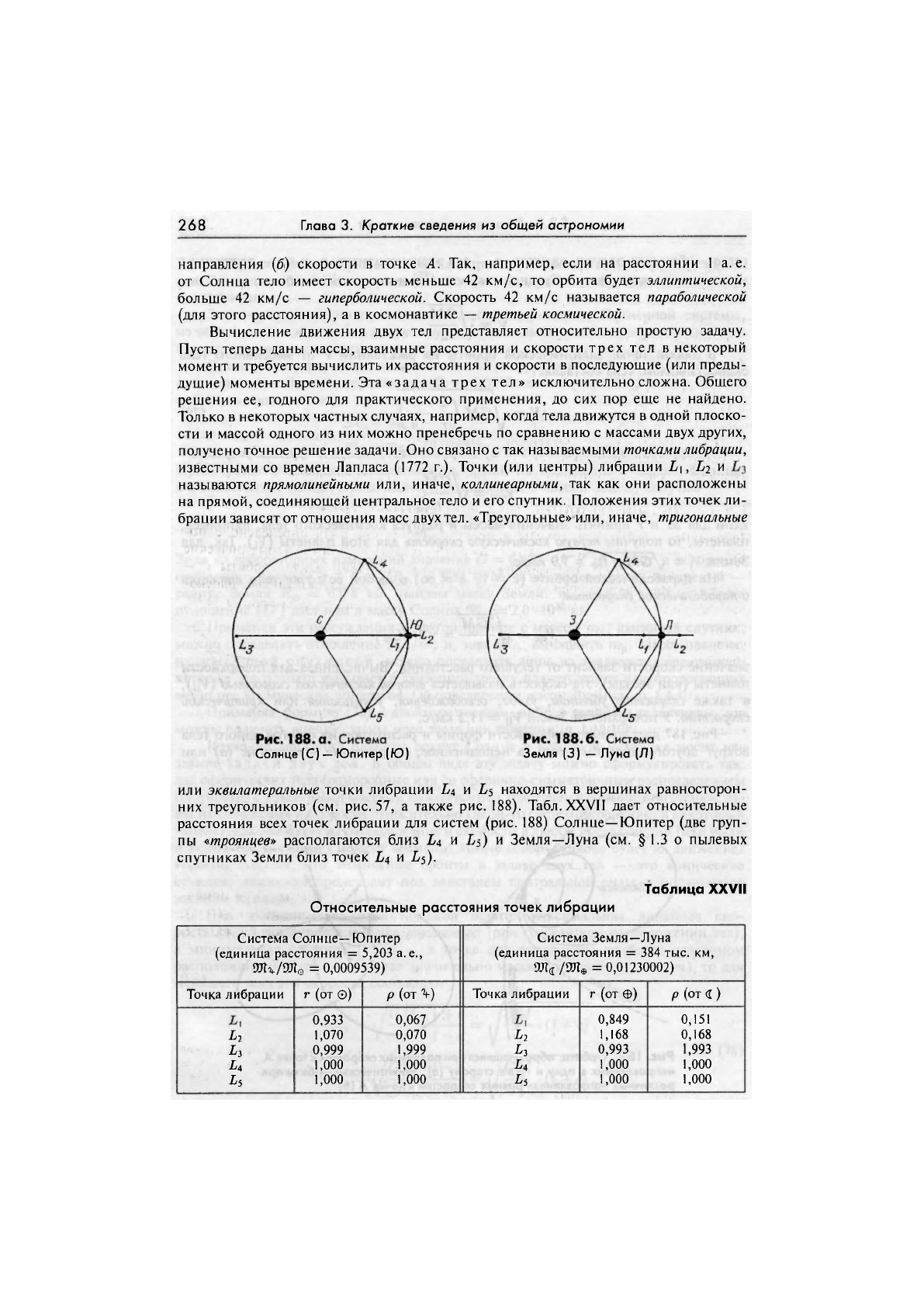
получено точное решение задачи. Оно связано с так называемыми точками либрации,

известными со времен Лапласа (1772 г.). Точки (или центры) либрации L\, Ь

называются прямолинейными или, иначе, коллинеарными, так как они расположены

на прямой, соединяющей центральное тело и его спутник. Положения этих точек ли-

брации зависят от отношения масс двух тел. «Треугольные» или, иначе, тригональные

Солнце (С) — Юпитер (Ю) Земля (3) — Луна (Л)

или эквилатеральные точки либрации Ь

и Ls находятся в вершинах равносторон-

них треугольников (см. рис.57, а также рис. 188). Табл.XXVII дает относительные

расстояния всех точек либрации для систем (рис. 188) Солнце—Юпитер (две груп-

пы «троянцев» располагаются близ L4 и Ь$) и Земля—Луна (см. § 1.3 о пылевых

спутниках Земли близ точек L

и L$).

Таблица XXVII

Относительные расстояния точек либрации

Система Солнце—Юпитер

Система Земля—Луна

(единица расстояния = 5,203 а. е.,

(единица расстояния = 384 тыс. км,

т%/Ш

= 0,0009539)

®?

/т е = 0,01230002)

Точка либрации

г (от 0) р (от \)

Точка либрации

г (от ф)

р (от

)

0,933

0,067 0,849

0,151

L 2

1,070

0,070

1,168 0,168

}

0,999 1,999 Li

0,993

1,993

1,000 1,000

1,000

1,000 1,000

§ 3.5. Движение планет и комет

269

Задача еще более усложняется, когда мы имеем дело с четырьмя и более телами,

как, например, со всей Солнечной системой, состоящей из тысячи тел.

Вычисление орбит и эфемерид тел Солнечной системы чрезвычайно облегча-

ется тем, что масса Солнца примерно в 750 раз больше, чем общая масса всех

остальных тел Солнечной системы, а масса даже самой большой планеты — Юпите-

ра—в 1047 раз меньше солнечной. Это позволяет, вычислив приближенную орбиту

какого-либо светила в рамках задачи двух тел (невозмущенное движение), в даль-

нейшем учесть сравнительно незначительные возмущения этой орбиты притяжением

других членов системы (в первую очередь Юпитера и Сатурна) и определить орбиту

и движение (возмущенное движение) тела с желаемой степенью точности.

Теоретической астрономией подробно разработаны методы вычисления элемен-

тов орбит планет и предвычисления эфемерид по данным наблюдений. Последние

десятилетия учет возмущений, вычисление орбит и эфемерид проводятся на ЭВМ.

3.5.1. Элементы планетных и кометных орбит

Положение планеты или кометы в пространстве может быть определено с по-

мощью шести элементов ее орбиты, из которых пять элементов геометрические

и один динамический. Эти элементы следующие (рис. 189): наклон орбиты г —

угол между плоскостью орбиты планеты и плоскостью эклиптики (иначе, плоско-

стью земной орбиты), гелиоцентрическая долгота восходящего узла орбиты

расстояние перигелия от узла ш,

большая полуось а, эксцентриси-

тет е, средняя аномалия Mg в эпо-

ху <о

или

момент прохождения че-

рез перигелий Го. Средняя анома-

лия — вспомогательная величина,

в каждый данный момент равная

дуге, которую описала бы плане-

та после своего прохождения через

перигелий, если бы она равномер-

но двигалась по круговой орбите,

имеющей диаметр 2а (вспомога-

тельная кеплерова окружность), за-

вершая полный оборот за период Р

обращения планеты (выраженный

в средних солнечных сутках)-.

Если 71° = 360°/Р назовем средним суточным движением планеты, Го

—

момен-

том прохождения перигелия, то в момент t средняя аномалия М будет М = n(t-To).

Линейная скорость движения планеты по орбите вычисляется для момента

по формуле

(80)

где р. = G(DJt

+ 9Л

лан), a G — гравитационная постоянная.

Восходящий узел соответствует той точке пересечения орбиты с плоскостью эклиптики, в которой

планета переходит из полусферы, содержащей южный полюс эклиптики, в полусферу, содержащую ее

северный полюс. При изучении движения ИСЗ за основную плоскость принимается плоскость земного

экватора и, соответственно, долгота считается вдоль небесного экватора.

270 Глава 3. Краткие сведения из общей астрономии

Период обращения (в годах) получим из третьего закона Кеплера: Р = у/а?,

если а выражено в астрономических единицах.

Наклон г считается от 0° до 180°. Углам г, большим 90°, соответствует обратное

движение по орбите

'. Расстояние перигелия от узла ш определяет ориентацию

орбиты в ее плоскости — это угол между линией узлов и большой осью орбиты; он

отсчитывается вдоль орбиты, в направлении движения планеты.

Иногда указывают долготу перигелия ш = fl + Угол ш, следовательно,

измеряется в двух плоскостях: в плоскости эклиптики от Т до £2 и потом в плоскости

орбиты планеты от £1 Д° П. В 1916 г. А.Эйнштейн указал, что одним из следствий

теории относительности должны быть вековые перемещения перигелиев планетных

орбит в направлении их орбитального движения, равные

24тг

(1 -

)с

2 Р

ад 33 1 об

°Р°

где с — скорость света. Для Меркурия Эйнштейн предсказал смещение +43,03"

в столетие, что совпало с величиной необъяснимого смещения, обнаруженного

из анализа многолетних наблюдений (42,84" ± 0,41"). Аналогичное смещение для

Венеры должно быть +8,7", для Земли +3,8", для Марса +1,35" в столетие

Форма орбиты определяется эксцентриситетом е = с/а, где с — расстояние

от центра эллипса до его фокуса. При эксцентриситетах, близких к нулю, форма

орбиты близка к окружности; при больших эксцентриситетах орбита имеет вид

весьма вытянутого эллипса. Иногда для удобства некоторых вычислений указывают

так называемый угол эксцентриситета ip, связанный с е соотношением

v^F ,

е = sin

(р

= , (81)

где b = aV 1

—

= a cos

<р

— малая ось эллипса.

Наибольшее расстояние планеты от Солнца (в афелии)

Q = г

—

(1 + е),

наименьшее (в перигелии)

q = г

= о(1 - е).

Так как орбиты комет обычно очень вытянуты и имеют очень большие а, то

в первом приближении их принимают за параболы, т.е. полагают е = 1, а = оо.

Новым линейным элементом принимают перигелийное расстояние q. Это упрощает

задачу определения элементов орбиты.

Когда элементы орбиты известны, можно решить обратную задачу: предвычи-

слить положения светила на небе (т.е. координаты а и <5) и расстояние от Земли р

для ряда моментов времени, т. е. вычислить так называемую эфемериду. Эфеме-

риды больших и малых планет и их спутников, Луны, а также Солнца, данные

о затмениях и других астрономических явлениях составляют основное содержание

астрономических ежегодников и календарей.

"'Для планет углы i небольшие и движение прямое; для комет г может быть любым и движение

может быть обратным.

'См. книгу: Роузвер Н. Т. Перигелий Меркурия: от Леверье до Эйнштейна. М.: Мир, 1985.