Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

Раздел 6

212

()



спектральной плотности возникают трудности. В тех

случаях, когда вид корреляционной функции заранее известен

или ясен из графика статистической корреляционной функции,

целесообразно подобрать соответствующее теоретическое вы-

ражение и по нему согласно (1.6) найти спектральную плот-

ность. Аппроксимация выполняется выражениями (1.8)-(1.10)

или их линейной комбинацией.

Если аппроксимация корреляционной функции затрудне-

на, то первоначально находят

оценку спектральной плотности –

либо по реализации помехи, либо по оценке корреляционной

функции.

Первый способ определения спектральной плотности по

реализации заключается в следующем. График помехи на ин-

тервале записи Т

разбивается на п интервалов (окон) меньшей

длительности Т

. На каждом r-ом интервале для значения ω уг-

ловой частоты по формулам коэффициентов ряда Фурье вычис-

ляется модуль С

νr

гармоники с такой же угловой частотой. Вы-

числения производятся для разных значений частот – в резуль-

тате получается зависимость С

νr

(ω), которую называют перио-

дограммой. По смыслу соответствующая ордината оценки спек-

тральной плотности представляет собой усредненное на ширине

окна значение квадрата амплитуды

() ()

νν

=ω

Искомая оценка

() ()

νν

∑



(6.3)

Общих рекомендаций по выбору ширины окна не сущест-

вует: она должна быть настолько большой, чтобы периодограм-

ма отражала свойства спектральной плотности, и в то же время

малой – чтобы количество п было большим. В связи с этим вы-

числения выполняют для разных значений Т

, начиная с малых.

Методы расчета показателей ЭМС по несинусоидальности напряжения

213

Вначале график спектральной плотности получается плавным,

так как ее пики на отдельных частотах будут сглажены. По мере

увеличения ширины окна пики проявляются все больше, но при

больших Т

на графике появляются пики, не присущие спек-

тральной плотности. «Оптимальным» является значение Т

, при

котором график спектральной плотности еще не приобретает

вида случайной функции.

Следует отметить, что периодограмму С

νr

(ω), вычислен-

ную за время записи графика, т.е. при п = 1, нельзя непосредст-

венно использовать для вычисления спектральной плотности

даже при Т

→ ∞. Для получения приемлемой точности вводят

усредняющее окно со спектральной весовой функцией g

(t), ко-

торая обращается в нуль при t > Т

[18, 43, 56]. Эту функцию

выражают в о.е. По ней выполняется прямое преобразование

Фурье

() () ()

00 0

cos cos

gt tdt gt tdt

∞

=ω=

ππ

∫∫

(6.4)

при условии, что середина окна приходится на момент времени,

равный нулю.

Оценка спектральной плотности при ω ≥ 0 имеет вид

(6.5)

()

() ( ) ( ) ()

,SRCdRC

∞∞

νν ν

ω= ξ ω−ξ ξ= ω−ξ ξ ξ

∫∫



где ξ – переменная интегрирования.

Известно большое количество окон [22, 29]. Самую про-

стую весовую функцию имеет окно Дирихле: в именованных

единицах согласно (1.27) она равна

1T ,

а в о.е. – единице. В

этом случае

()

000

sinc 2 .RTTω= ω

Раздел 6

214

Для окна Бартлетта при t ≤ Т

справедливы выражения:

() ()

()

0000

12 , sinc 2.gt tT R T T=− ω= ω

Второй способ основан на соотношении (2.47): помеха

пропускается через узкополосные фильтры, настроенные на

разные частоты. Полоса пропускания на каждой частоте выби-

рается настолько малой, чтобы в ее пределах АЧФ фильтра была

почти постоянной, равной единице, а за пределами полосы –

равной нулю. Длительность реализации помехи должна быть

настолько большой, чтобы не только

исключить участок пере-

ходного процесса на выходе фильтра, но и получить после этого

продолжительный участок стационарного состояния, достаточ-

ный для вычисления стандарта σ

с небольшой погрешностью.

Так как квадрат стандарта равен интегралу от спектральной

плотности в пределах полосы ∆ω пропускания, то

()

=σ ∆ω



(6.6)

Для определения спектральной плотности в действующих

сетях можно использовать анализатор гармоник, настраиваемый

на любые частоты, а не только кратные 50 Гц. На выбранной

частоте прибор показывает именно стандарт σ

– для примене-

ния формулы (6.6) необходимо знать лишь полосу пропускания

фильтра. Отсчет производится в стационарном состоянии, когда

показания прибора не изменяются. Если это состояние не насту-

пает, то процесс нельзя считать стационарным.

Перейдем к определению оценки спектральной плотности

по оценке корреляционной функции. Для этой цели нельзя ис-

пользовать преобразование (1.6), так как

оно предполагает, что

корреляционная функция задана на бесконечном интервале. Да-

же при большой длительности записи оценку корреляционной

функции с достаточной точностью можно выполнить лишь на

начальном участке значений ее аргумента. В результате оценка

спектральной плотности сильно искажается – вплоть до появле-

Методы расчета показателей ЭМС по несинусоидальности напряжения

215

ния отрицательных ординат, что противоречит физическому

смыслу.

Приемлемая оценка, равноценная (6.5), получается, если в

формулу для спектральной плотности ввести спектральную ве-

совую функцию. В этом случае получим

() () ()

.SgK

∞

=ττ

∫



(6.7)

Как и при применении формулы (6.3), выбор интервала Т

выполняется путем подбора.

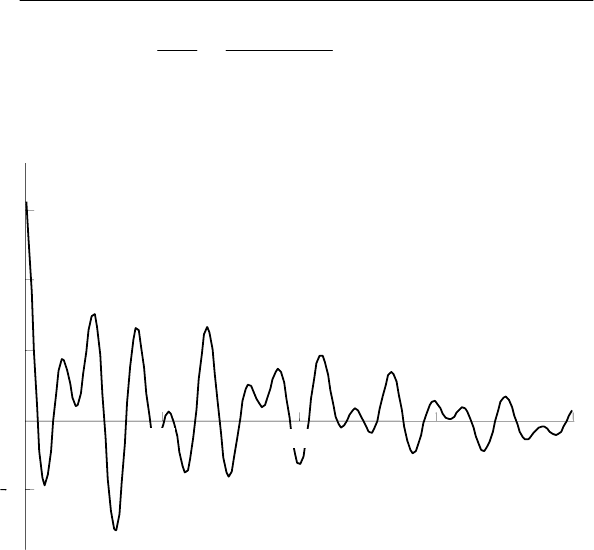
На рис. 6.3 показана статистическая корреляционная

функция, рассчитанная по графику помехи длительностью Т

0,32 с, частично представленной на рис. 6.1,б. Корреляционная

функция хорошо аппроксимируется выражением

()

{}

exp cos ,

νν

=−ατ

∑

ωτ (6.8)

в которой D

ν1

= 4,59, D

ν2

= D

ν3

= 6,065 (%)

; α

= 14, α

= α

50 с

–1

; ω

= 258, ω

= 2330, ω

= 1420 с

–1

. С учетом (1.13) най-

дем спектральную плотность

()

() ()

211

rrrr

νν

⎡

⎤

ω= α +

⎢

⎥

α+ω+ω α+ω−ω

⎣

⎦

∑

(6.9)

которая представлена графически на рис. 5.3.

В п. 1.3 получена формула для времени корреляции поме-

хи с экспоненциально-косинусоидальной корреляционной

функцией. В выражение (6.8) входят три слагаемых такого типа.

Доля каждого из них при определении общего времени корре-

ляции есть отношение соответствующей дисперсии D

νr

к их

сумме, которая равна дисперсии помехи. В результате при

0rr∗

α=αω

получим

Раздел 6

216

()

(

csch .

∗ν

∗

∗∗

)

=α

α+α

∑

+ϕ

(6.10)

Для графика на рис. 6.1,б время корреляции равно 0,73 мс.

0,01

0,02 0,03 0,04

(%)

, с

Рис. 6.3. Корреляционная функция несинусоидальной

компоненты напряжения на шинах 6 кВ подстанции металлур-

гического завода при работе ДСП

При больших постоянных времени нагрева используются

коэффициенты искажения. Преобразование (5.5) настолько

сильно сглаживает помеху, что даже график z

(t) квадратов ко-

эффициентов искажения имеет относительно малую неравно-

мерность. Это является большим достоинством предварительно-

го усреднения, так как корреляционная функция В

(τ) квадра-

тов коэффициентов искажения является более плавной, чем да-

же корреляционная функция помехи, а тем более квадратов по-

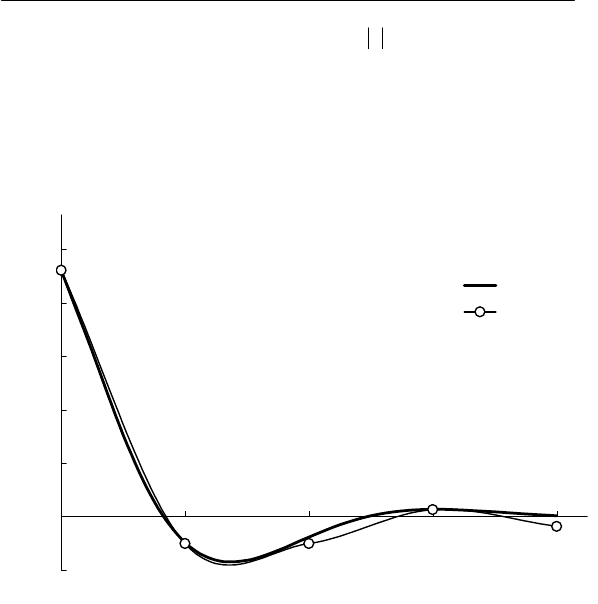
мехи. На рис. 6.4 кружками показаны значения статистической

корреляционной функции, которая хорошо аппроксимируется

выражением

Методы расчета показателей ЭМС по несинусоидальности напряжения

217

()

{

}

exp cos

UUz

BDz

=−ατωτ (6.11)

с дисперсией

= 6,09 (%)

и параметрами α

= 56 с

–1

= 95 с

–1

. Погрешность аппроксимации по отношению к дис-

персии не превысила 4,37 %. Время корреляции (п. 1.3) равно

0,012 секунды.

-10

0 0,02 0,04 0,06 0,08

Теория

Опыт

(%)

(τ)

Рис. 6.4. Корреляционная функция квадратов коэффици-

ентов искажения напряжения на шинах 6 кВ

Ввиду сложности определения корреляционной функции

и спектральной плотности, целесообразно стремиться к заданию

исходной информации в виде реализации помехи. Для целей

проектирования надо создавать банк реализаций токов типич-

ных источников помехи.

6.3. Расчет инерционных и кумулятивных коэффициентов

искажений

Расчет инерционных коэффициентов искажения K

ана-

логичен расчету инерционных коэффициентов несимметрии

Раздел 6

218

(п.п. 4.6 и 4.7). Если исходной является реализация процесса

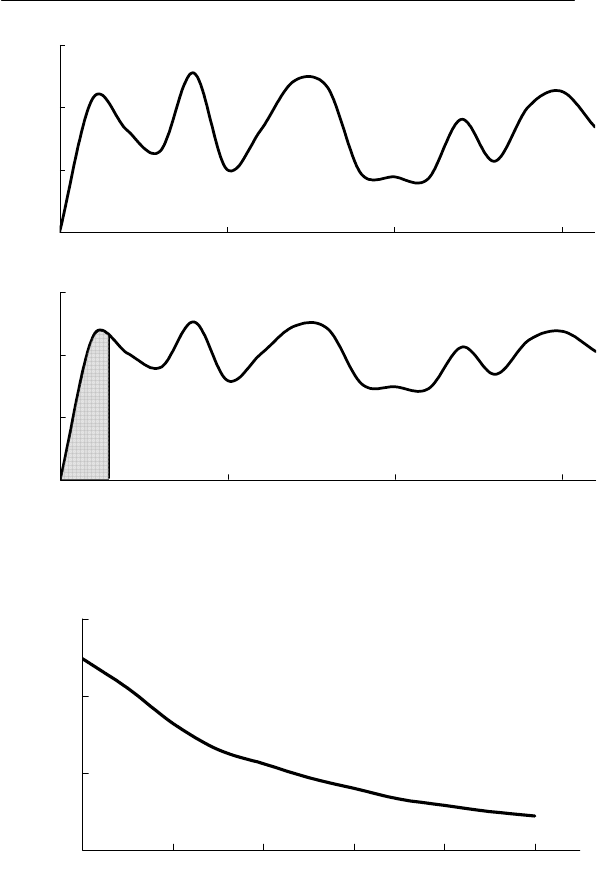
(t) (например, рис. 6.2), то после возведения ее в квадрат (рис.

6.5,а) ординаты квадратичного процесса в конце r-ой ступени

вычисляются по аналогичной (4.53) формуле

(

)

1 при 1, , 1.

Tr T r U

wwbK b r N

νν∆ ∆

+− = −…

(6.12)

Начальная ордината при t = 0 принимается равной нулю.

Извлечением квадратного корня получается график приведен-

ных коэффициентов искажения K

(рис. 6.5,б). Стационарное

состояние практически наступает спустя 3Т после начала пере-

ходного процесса (затушеванная область). По этому графику

строится статистическая функция распределения и с граничной

вероятностью 0,05 определяется расчетное максимальное значе-

ние K

UTmax

инерционного коэффициента искажения. Расчеты по-

вторяются для разных значений постоянной времени – в резуль-

тате получается Т-характеристика (рис. 6.6).

В рассматриваемом примере уже при постоянных време-

ни, превышающих 0,08 секунд, с погрешностью менее 5 % оце-

нивание ЭМС можно выполнять по эффективному значению K

Uэ

исходного графика коэффициента искажения, которое оказалось

равным 4,1 %.

График кумулятивных коэффициентов искажения K

Uθ

(t)

строится точно так же, как и кумулятивный график несиммет-

рии на рис. 4.5. В примере нормируемая длительность осредне-

ния в 3 с намного больше средней длительности между сосед-

ними максимумами исходного графика на рис. 6.2, поэтому до-

пускаемое для сети 6 кВ значение 5 % должно сравниваться с

эффективным значением. Поскольку 4,1 % меньше нормы, тре-

бования

[6] не нарушаются.

Если задан не график, а вероятностные характеристики

коэффициента искажения, то расчет выполняется по аналогич-

ным формулам, приведенным в п.п. 4.5 и 4.7 для коэффициента

несимметрии напряжения: достаточно заменить корреляцион-

ную функцию B

(τ) на B

(τ), а коэффициент K

на K

Методы расчета показателей ЭМС по несинусоидальности напряжения

219

00,10,2

(%)

0,3

00,10,20,3

% K

3Т

Рис. 6.5. К построению графика инерционных коэффици-

ентов искажений в сети 6 кВ при Т = 0,01 с

4,5

5,5

0 0,02 0,04 0,06 0,08 0,1

% K

UTmax

Рис. 6.6. Зависимость инерционных максимумов коэффи-

циентов искажений напряжения в сети 6 кВ от постоянной вре-

мени нагрева

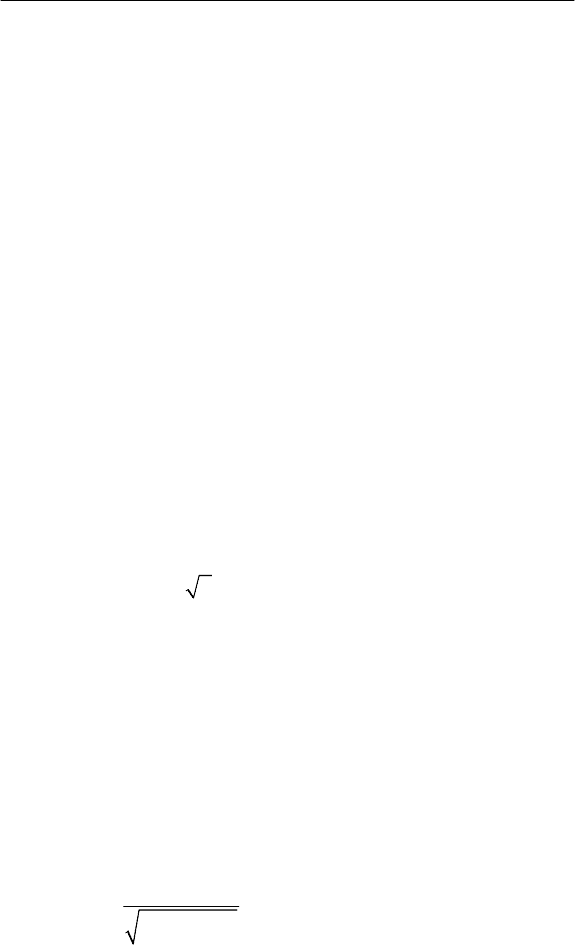
Раздел 6

220

6.4. Оценивание влияния несинусоидальности напряжения

на электродвигатели

Как показано в п. 5.3, ВФ модели ЭМС двигателей пред-

ставляет собой инерционное звено с параметрами а

дν

= 0,713 и

дν

= 0,00123 с (звено 2 на рис. 5.6). Поскольку постоянная вре-

мени отличается от 0,02 с, использовать коэффициенты искаже-

ния нельзя, а надо исходить из графика помехи. Так как посто-

янные времени нагрева двигателей велики, оценивание ЭМС

осуществляется по эффективному значению i

νэ

несинусоидаль-

ной компоненты тока двигателя.

В частном случае периодической помехи с длительностью

цикла t

решение может быть получено тремя способами: мето-

дами гармонического анализа, по графику помехи и по корреля-

ционной функции помехи.

Рассмотрим первый способ, когда помеха представляется

в виде ряда Фурье

()

(

min

sin

Un f n

ut u B n t

∞

νν

)

+ω

∑

+ϕ

(6.13)

с амплитудами

в 2 превышающими коэффициенты гар-

моник и фазами

Нижний предел суммы п

min

= 1, если неси-

нусоидальная компонента выделяется по неискаженной части

синусоиды, и 2 – в противном случае (п. 5.1).

С учетом формул (1.24) и (2.45) получены следующие ха-

рактеристики реакции: среднее значение

сдс

,iau

νν

(6.14)

амплитуда и фаза тока п-ой гармоники

22 2

,arctg

In In n f

=ϕ=ϕ−

+ω

(6.15)

Методы расчета показателей ЭМС по несинусоидальности напряжения

221

Вследствие некоррелированности гармоник, эффективное

значение не зависит от фаз гармоник:

min min

22 2

эс дс

22 2

ii Bau

∞∞

νν νν

=+ = +

+ω

∑∑

(6.16)

Погрешность вычисления эффективного значения, как ин-

тегральной характеристики, невелика даже для недифференци-

руемой помехи, а если исходный процесс задан аналитическим

выражением, погрешность отсутствует.

Перейдем ко второму способу. Здесь реакция ВФ опреде-

ляется для стационарного режима без вычисления переходного

процесса. Алгоритм решения аналогичен изложенному в п. 2.5

для квадратичного инерционного процесса, но

без возведения

исходного графика в квадрат.

Пусть в пределах цикла имеется N участков, а в пределах

r-го участка длительностью t

помеха описывается функцией

νr

(t) при r = 1, 2, …, N. Обозначим:

{

}

()

{}

дд д

1, exp

И exp .

rr r

Tb t

ut tdt

γ= = −γ

=γ

∫

На каждом участке время будем отсчитывать от начала

участка. Решение дифференциального уравнения (1.21) имеет

вид

() ()

{

}

ндд д

И exp ,

rr r

it i a t t

ννν

⎡⎤=+γ −γ

⎣⎦

(6.17)

где i

νrн

– неизвестная пока начальная ордината реакции на r-ом

участке. Подставив сюда длительности участков, получим N вы-

ражений для ординат на концах участков: