Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_77 next page >

Page 77

(3) VP→V·NP.

We also include amongst these rules the specific English words that belong to those grammatical

categories consisting only of words; the symbol ‘|’ should be read ‘or’:

(4) T→the.

(5) N→girl|boy|ball|bat|frisbee.

(6) V→hit|took|threw|lost.

We can use this grammar to generate a language over the alphabet:

The starting point is always the symbol S. Here is one example; we use the symbol when we are

generating a sentence.

• S NP·VP.

• NP·VP T·N·VP.

• T·N·VP T·N·V·NP.

• T·N·V·NP T·N·V·T·N.

• T·N·V·T·N the N·V·T·N.

• the N·V·T·N the boy V·T·N.

• the boy V·T·N the boy threw T·N.

• the boy threw T·N the boy threw the N.

• the boy threw the N the boy threw the ball.

We see that the string ‘the boy threw the ball’ belongs to the language generated by the grammar.

The above example is not a very good representation of English; in fact, writing descriptions of natural

languages is a complex business and the subject of intensive research. Our next example is much more

representative of what we shall be dealing with. But first we need some terminology.

The symbols ‘the,’ ‘man,’ ‘ball,’ ‘took,’ ‘hit’ etc. are called terminals. It is important to note that we are

thinking of the words ‘the,’ ‘man,’ ‘ball,’ etc. as being individual symbols not strings. The grammatical

categories are called non-terminals. The rules are called productions, and S is called the start symbol.

The language we constructed was over the alphabet consisting of the set of terminals.

< previous page page_77 next page >

< previous page page_78 next page >

Page 78

Example 3.5.2 The following is a grammar for a fragment of a PASCAL-type language called the

‘language of while-programs.’ The set of non-terminals is: program , statement sequence ,

statement , asgt , test , variable , digit .

The set of terminals is

together with

and

and the start symbol is program .

The productions are as follows:

(1) program →begin end|begin statement sequence end.

(2)

statement sequence → statement | statement sequence ; statement .

(3)

statement → asgt |while test do statement | program .

(4)

test → variable ≠ variable .

(5)

asgt → variable := 0| variable :=

succ

( variable )| variable :=

pred

( variable ).

(6)

variable → alpha | variable alpha | variable digit .

(7)

digit →0|1|…|9.

(8)

alpha →

|…|

An example of a string in the language generated by this grammar is

which we leave to the reader to check.

We now make precise what we mean by a ‘grammar.’ A

grammar

is a 4-tuple G=

(N, A, P, S)

consisting

of the following

•

is a finite set of

non-terminal symbols

•

is a set of

terminal symbols

; we have that .

• is the

start symbol

< previous page page_78 next page >

< previous page page_79 next page >

Page 79

•

is a finite set of

productions

; each production is of the form

→

where

x, y

are strings in (

such that

x contains at least one non-terminal symbol

Grammars are devices for

generating

the strings in a language. To see how they accomplish this, we

need the following definitions and notation. Let

→

be a production in a grammar G. Let

. Suppose that

Then we say

w′ is immediately derived from w

in the grammar G. We denote this by

Let

,…, wn

be a sequence of strings in (

)* such that

Then we say that

derivable from w

1 and denote this by

The sequence

,…, wn

is called a

derivation of wnfrom w

in the grammar

G. The

language generated

G is:

the set of all strings over the terminal alphabet, which can be derived from the start symbol. A language

is said to be

recursively enumerable (re)

if there is a grammar G such that

(G). Recursively

enumerable languages are very closely related to Turing machines: see the remarks at the end of this

chapter.

We give three more examples of grammars before we make explicit the connection between finite

automata and a special class of grammars.

Example 3.5.3 The grammar G3=

({A, S}, {a, b, c}, P, S)

where

has the following productions:

On this occasion, I have numbered the productions so that those used in a derivation may be recorded.

In the production (1), we use the symbol|to mean ‘or’, so that we really have two productions:

→

abASc

and

→

. Here is a derivation of

2 from this grammar:

In this derivation, I have underlined, for the sake of clarity, those portions of a string to which a

production is applied.

< previous page page_79 next page >

< previous page page_80 next page >

Page 80

Example 3.5.4 The grammar G4=

({S}, {a, b}, P, S)

has productions:

The language generated by this grammar is {

anbn: n

≥0}.

Example 3.5.5 The grammar G5=(

{S, A, B},

{0, 1},

P, S

) where

has the following productions:

The language generated by this grammar is (10)*1.

We have given five examples of grammars: Examples 3.5.1–3.5.5. The grammar in Example 3.5.3 stands

out as being different: in all the other grammars, the left-hand side of each production consists of a

single non-terminal, whereas in Example 3.5.3 there are productions where the left-hand side contains a

mixture of terminals and non-terminals or contains more than one terminal. Grammars like Example

3.5.3 are usually much harder to work with. For this reason we single out the ‘nice’ cases. A grammar is

said to be

context-free (CF)

if each production

→

is such that

is a single non-terminal. A language

is said to be

context-free

if there is a context-free grammar G such that

(G)=

. Context-free

languages are the basis for describing programming languages as Example 3.5.2 suggests. However,

they are still too general for our purposes. Example 3.5.5 is an example of the kind of grammar that will

interest us. A grammar is said to be

right linear

if each production has one of the following forms:

•

→

•

→

•

→

where and . From now on we shall deal solely with right linear grammars; this is because

of the following result: a language can be described by a right linear grammar if and only if it is

recognisable. To prove this result, we first need a lemma.

Lemma 3.5.6

Let

(N, V, P, S) be a right linear grammar

Then we can always assume that the only

productions in P have the form A

→

bC or A

→

Proof Suppose we have a production of the form

→

. Introduce a

new

non-terminal

such that

and replace

→

and

→

. It is clear that the new grammar G′ we obtain satisfies

(G′)=

(G). This procedure is repeated until all productions of the form

→

have been eradicated. In

each case, the new symbol

can be re-used.

We now come to the result that links right linear grammars and the languages that interest us.

< previous page page_80 next page >

< previous page page_81 next page >

Page 81

Theorem 3.5.7

A language is generated by a right linear grammar if and only if it is recognisable.

Proof Let G=

(N, V, P, S)

be a right linear grammar, which by Lemma 3.5.6 we can assume to have

productions only of the form

→

. We shall construct a non-deterministic automaton A=

(Q, A,

i, δ, T)

from G and prove that

(A)=

(G). We define A as follows:

• The states

are labelled by the non-terminals.

• The initial state

is labelled by

the start symbol.

• The set of terminal states

is labelled by those non-terminals

for which

→

is a production in

It only remains to define

. This is done as follows: for each production we construct a

transition:

It is clear that A is a non-deterministic automaton (in general). It remains to prove that

(A)=

(G).

Observe first that the initial state of A is also terminal if and only if the production

→

belongs to

Thus

iff . Let be a non-empty string where

1…

. Then there is a

derivation,

where the productions used are

This corresponds to the following sequence of transitions in A:

Consequently . It is clear that this argument works in reverse. We deduce that

(A)=

(G).

Now let A=

(Q, V, I, δ, T)

be a deterministic automaton. We shall define a right linear grammar G=

(N,

V, P, S)

such that

(G)=

(A). We define G as follows:

• The set of terminals

is labelled by the states

• The start symbol

is the initial state

< previous page page_81 next page >

< previous page page_82 next page >

Page 82

It only remains to define

. If then

→

is in

δ(A, c)

then

→

is in

. Clearly G is a

right-linear grammar. Once again it is easy to check that

iff . Now let

. Then there is a path in A labelled by

which begins at

and ends at a terminal

state:

This implies that we have the following productions in

Hence . It is clear that this argument works in reverse. We deduce that

(G)=

(A).

Exercises 3.5

1. In Example 3.5.1, derive the sentence: the boy lost the frisbee.

2. In Example 3.5.2, derive the string:

3. In Example 3.5.3, derive the string:

4. Find a right linear grammar that generates the language accepted by the following machine:

5. Find a non-deterministic automaton that recognises the language generated by the grammar,

where

consists of the following productions:

6. Consider the following context free grammar G=

(N, V, P, S)

where

{S}

and

consists of the

following productions:

Is the language generated by this grammar recognisable or not? Justify your answer.

< previous page page_82 next page >

< previous page page_83 next page >

Page 83

3.6 Summary of Chapter 3

•

Accessible automata:

A state

is accessible if there is an input string that labels a path starting at the

initial state and ending at the state

. An automaton is accessible if every state is accessible. If A is an

automaton, then the accessible part of A, denoted by A

, is obtained by removing all inaccessible states

and transitions to and from them. The language remains unaltered. There is an efficient algorithm for

constructing A

using the transition tree of A.

•

Non-deterministic automata:

These are automata where the restrictions of completeness and

determinism are renounced and where we are allowed to have a set of initial states. A string is accepted

by such a machine if it labels at least one path from an initial state to a terminal state. If A is a non-

deterministic automaton, then there is an algorithm, called the subset construction, which constructs a

deterministic automaton, denoted A

, recognising the same language as A. The disadvantage of this

construction is that the states of A

are labelled by the subsets of the set of states of A. The accessible

subset construction constructs the automaton (A

)

directly from A and often leads to a much

smaller automaton.

•

Applications of non-deterministic automata:

Let A be a non-deterministic automaton. Then Arev, the

reverse of A, is obtained by reversing all the transitions in A and interchanging initial and terminal

states. The language recognised by Arev is the reverse of the language recognised by A. If

and

are

recognisable, then we can prove that

M, L

and

* are each recognisable using non-deterministic

automata.

•

Trim automata:

If A is a non-deterministic automaton we can define its accessible part A

and its co-

accessible part A

. If we carry out both of these constructions, in either order, we obtain A

, the trim

part of A. None of these constructions changes the language.

•

Grammars:

Grammars are devices for generating the strings in a language. The class of right linear

grammars generates precisely the recognisable languages.

3.7 Remarks on Chapter 3

I learnt about transition trees from Büchi’s book [22]. Many of the results in Sections 3.2, 3.3, and 3.4,

including the subset construction, can be found in [109]; Eilenberg [39] states (page 74) that virtually

everything known about automata up to 1959 was presented in this paper. You can read about how

Scott and Rabin came to work on non-deterministic automata in [119]. I

< previous page page_83 next page >

< previous page page_84 next page >

Page 84

learnt about trim automata and their applications from [39]. The grammatical approach to recognisable

languages is from [29].

With the introduction of grammars, I can now sketch out the class of all languages. The largest class

studied in automata theory are those that can be recognised by Turing machines; these turn out to be

precisely the recursively enumerable languages. By the Church-Turing Thesis, the membership problem

for languages that are not recursively enumerable cannot be solved by algorithmic means. The next

class consists of those languages that can be generated by context-free grammars. The corresponding

class of automata that recognise such languages are the so-called ‘pushdown automata,’ which can be

regarded as consisting of a finite automaton with access to a memory in the form of a pushdown stack.

Finally, we have the class of languages generated by right linear grammars which, as we have proved,

are precisely the languages recognised by finite automata. This hierarchy of languages is called the

Chomsky hierarchy

. This book is solely concerned with the lowest rung of this hierarchy of languages.

If you want to learn more about languages, automata, and grammars, then [66] and [80] are good

references. The source for Example 3.5.1 is Chomsky [28], and for Example 3.5.2 Kfoury et al. [73]. The

book by Kfoury provides an alternative approach to the study of algorithms via this simple programming

language. Finally, finite automata and context-free languages together provide the setting for designing

compilers; see the ‘red dragon book’ [1].

< previous page page_84 next page >

< previous page page_85 next page >

Page 85

Chapter 4

-automata

Non-deterministic and deterministic automata have something in common: both types of machines can

only change state as a response to reading an input symbol. In the case of non-deterministic automata,

a state and an input symbol lead to a set of possible states. The class of

-automata, introduced in this

chapter, can change state spontaneously without any input symbol being read. Although this sounds like

a very powerful feature, we shall show that every non-deterministic automaton with

-transitions can be

converted into a non-deterministic automaton without

-transitions that recognises the same language.

Armed with

-automata, we can construct automata to recognise all kinds of languages with great ease.

Our main application of ε-automata will be in Section 5.3.

4.1 Automata with

-transitions

In both deterministic and non-deterministic automata, transitions may only be labelled with elements of

the input alphabet. No edge may be labelled with the empty string

. We shall now waive this

restriction. A

non-deterministic automaton with ε-transitions

or, more simply, an

ε-automaton,

is a 5-

tuple,

where all the symbols have the same meanings as in the non-deterministic case except that

As before, we shall write

δε(s, a)

. The only difference between such automata and non-

deterministic automata is that we allow transitions:

Such transitions are called

ε-transitions

< previous page page_85 next page >

< previous page page_86 next page >

Page 86

In order to define what we mean by the language accepted by such a machine, we have to define an

appropriate ‘extended transition function.’ This is slightly more involved than before, so I shall begin

with an informal description. A path in an

-automaton is a sequence of states each labelled by an

element of the set

. The string corresponding to this path is the

concatenation

of these labels in

order. We say that a string

is accepted by an

-automaton if there is a path from an initial state to a

terminal state the concatenation of whose labels is

. I now have to put this idea on a sound footing.

Let

be an alphabet. If

then for all we have that

εmaεn

. However,

εmaεn

is also a

string

consisting of

m ε

’s followed by one

followed by a further

n ε

’s. We call this string an

ε-extension

of the symbol

. The

value

of the

-extension

εmaεn

. More generally, we can define an

-extension

of a string

to be the product of

-extensions of each symbol in

. The value of any such

extension is just

. For example, the string

aba

has

-extensions of the form

εmaεnbεpaεq,

where

. Let A be a non-deterministic automaton with

-transitions. We say that

accepted by

some ε

-extension of

labels a path in A starting at some initial state and ending at some terminal

state. As usual we write

(A) to mean the set of all strings accepted by A. It is now time for a concrete

example.

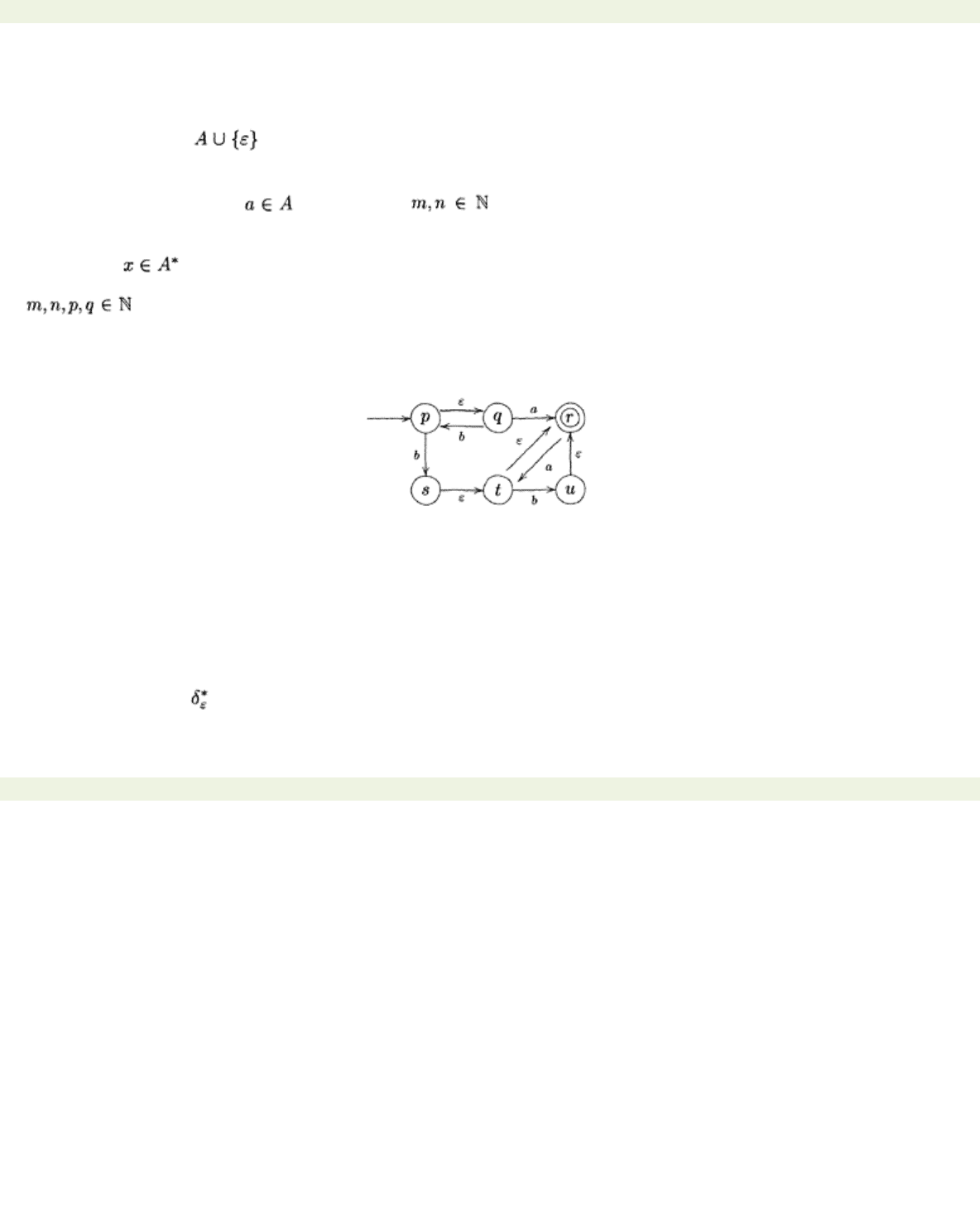
Example 4.1.1 Consider the diagram below:

This is clearly a non-deterministic automaton with

-transitions. We find some examples of strings

accepted by this machine. First of all, the letter

is accepted. At first sight, this looks wrong, because

there are no transitions from

labelled by

. However, this is not our definition of how a string is

accepted. We have to check

all possible ε-extensions of a

. In this case, we immediately see that

εa

labels a path from

and so

a is

accepted. Notice, by the way, that it is the

value

of the

extension that is accepted; so, if you said

εa

was accepted, I would have to say that you were wrong.

The letter

is accepted, because

bεε

labels a path from

. The string

is accepted, because

bεbε

labels a path from

Now that we understand how

-automata are supposed to behave, we can formally define the extended

transition function . To do this, we shall use the following definition. Let A be a non-deterministic

automaton with

ε-

transitions, and let

be an arbitrary state of A. The

ε-closure of s,

denoted by

E(s),

consists of

itself together with all states in A, which can be reached

< previous page page_86 next page >