Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_87 next page >

Page 87

by following paths labelled

only

’s. If

is a set of states, then we define the

ε-closure of Q

the union of the

-closures of each of the states in

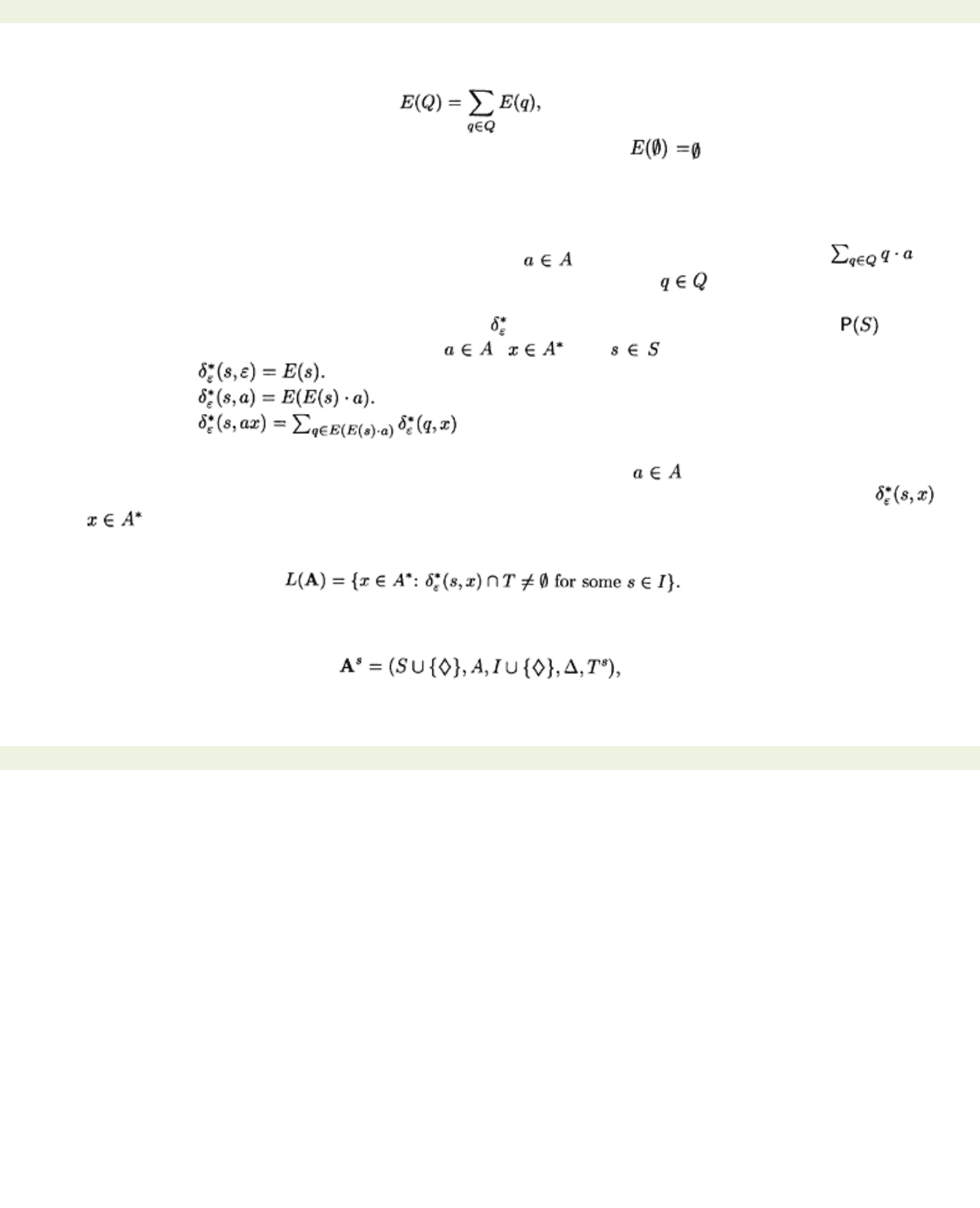
. Observe that . Referring to Example

4.1.1, the reader should check that

E(p)

{p, q}, E(q)

{q}, E(r)={r}, E(s)

{s, t, r}, E(t)

{t, r},

and

E(u)

{u, r}

. The only point that needs to be emphasised is that the

-closure of a state must contain

that state, and so it can never be empty.

We are almost ready to define the extended transition function. We need one piece of notation.

Notation If

is a set of states in an

-automaton and then we write

to mean

;

that is, a state

belongs to the set

precisely when there is a state and a transition in A from

labelled by

The

extended transition function

of an

-automaton is the unique function from

* to

satisfying the following three conditions where , and

(ETF1)

(ETF2)

(ETF3)

Once again, it can be shown that this defines a unique function. This definition agrees perfectly with our

definition of the

-extension of a string. To see why, observe that if

then

E(E(s)·a)

is the set of

states that can be reached starting at

and following all paths labelled

εmaεn

. More generally,

where

consists of all states that can be reached starting at

and following all paths labelled by

-extensions of

. We conclude that the appropriate definition of the language accepted by an

automaton is

Our goal now is to show that a language recognised by an

-automaton can be recognised by an

ordinary non-deterministic automaton. To do this, we shall use the following construction. Let A=

(S, A,

I, δε, T)

be a non-deterministic automaton with

-transitions. Define a non-deterministic automaton,

as follows:

• ◊ is a new state.

< previous page page_87 next page >

< previous page page_88 next page >

Page 88

•

• The function,

is defined as follows: for all

and Δ

(s, a)

E(E(s)

for all and .

It is clear that A

is a well-defined, non-deterministic automaton. Observe that the role of the state ◊ is

solely to accept

if . If

then you can omit ◊ from the construction of A

Theorem 4.1.2

Let

(S, A, I, δε, T) be a non-deterministic automaton with ε-transitions

Then

(A).

Proof The main plank of the proof is the following equation, which we shall prove below: for all

and we have that

(4.1)

Observe that this equation holds for

non-empty

strings. We prove (4.1) by induction on the length of

For the base step, let

. Then

simply following the definitions.

For the induction step, assume that the equality holds for all

where |

. Let

where

and |

. Then

by the definition of Δ*. By the base step and the induction step,

but by definition,

and we have proved the equality.

Now we can prove that

(A). Observe first that

< previous page page_88 next page >

< previous page page_89 next page >

Page 89

With this case out of the way, let

. Then by definition means that there is some

such that . But since

is not empty, the state ◊ can play no role and so we

can write that for some

we have . By equation (4.1), . Thus

if and only if for some . This of course says precisely that as

required.

Remark The meaning of the ‘s’ in A

is that of ‘sans’ since A

is ‘sans epsilons.’

The construction of the machine A

is quite involved. It is best to set the calculations out in tabular form

as suggested by the following example.

Example 4.1.3 We calculate A for the

-automaton of Example 4.1.1.

The last two columns give us the information required to construct A

below:

In this case, the state labelled is omitted because the original automaton does not accept the empty

string.

< previous page page_89 next page >

< previous page page_90 next page >

Page 90

Exercises 4.1

1. For each of the

-automata A below construct A

and A

sda=

((A

)

. In each case, describe

(A).

(i)

(ii)

(iii)

4.2 Applications of

-automata

and

are both recognisable, then

-automata provide a simple way of proving that

M, LM

and

* are all recognisable. We shall use these versions of the proofs when we prove the algorithmic form of

Kleene’s theorem in Section 5.3.

Theorem 4.2.1

Let A be an alphabet and L and M be languages over A.

(i)

If L and M are recognisable then L

M is recognisable

(ii)

If L and M are recognisable then LM is recognisable.

(iii)

If L is recognisable then L

is recognisable

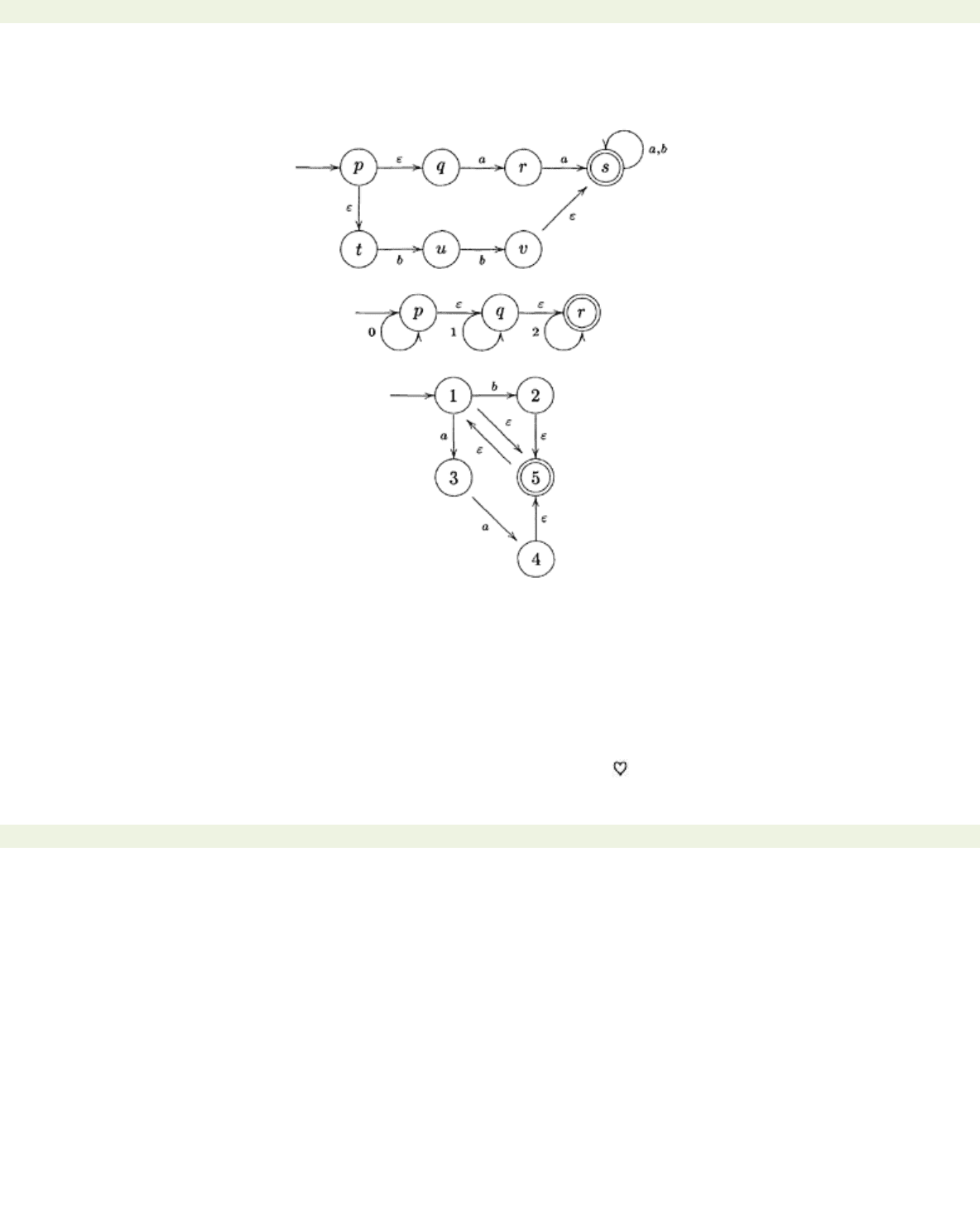
Proof (i) By assumption, we are given two automata A and B such that

(A)=

and

(B)=

. Construct

the following

-automaton: introduce a new state, which we label , to be the new initial state and

draw

-transitions

< previous page page_90 next page >

< previous page page_91 next page >

Page 91

to the initial state of A and the initial state of B; the initial states of A and B are now converted into

ordinary states. Call the resulting

-automaton C. It is clear that this machine recognises the language

. We now apply Theorem 4.1.2 to obtain a non-deterministic automaton recognising

. Thus

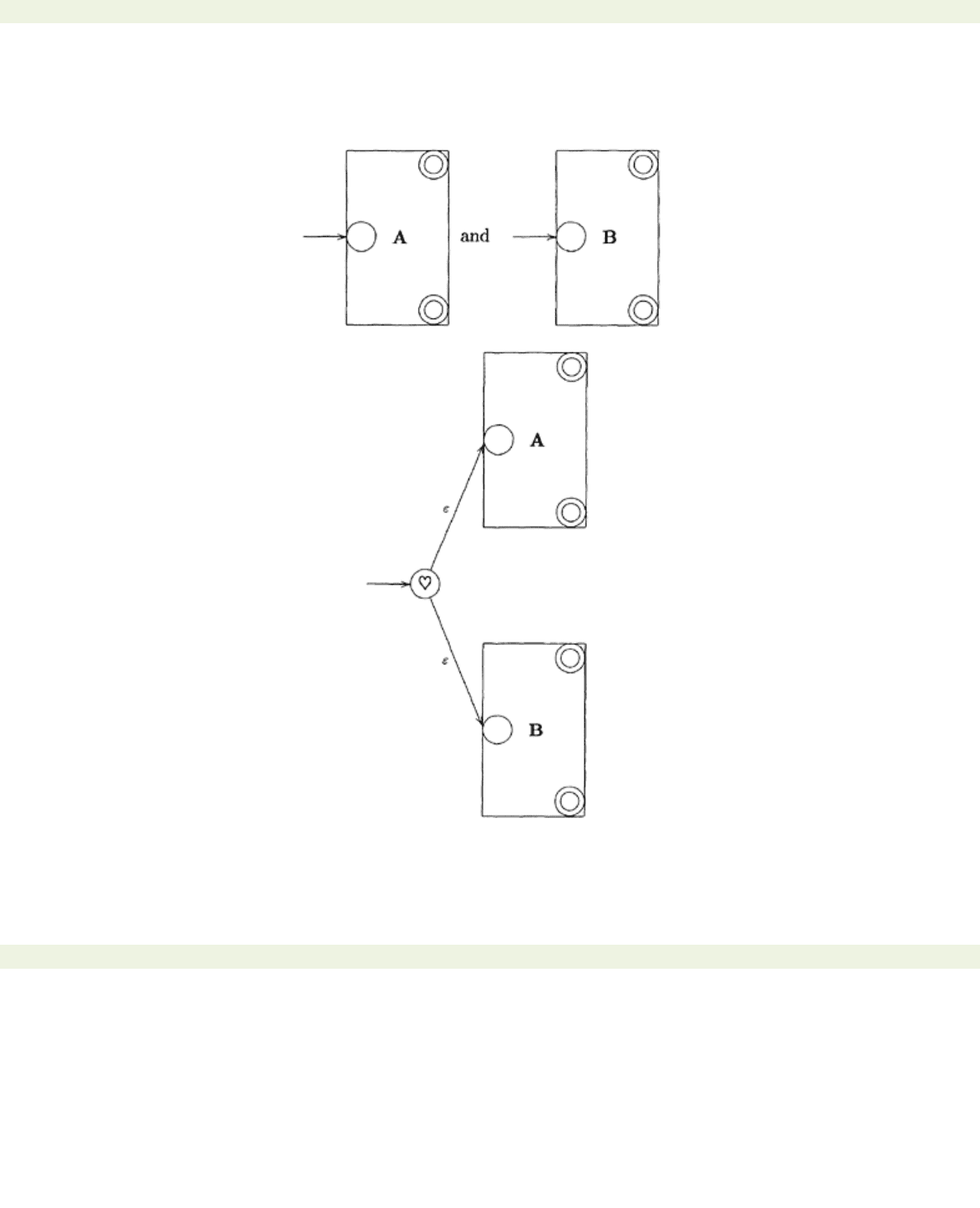
is recognisable. If we picture A and B schematically as follows:

Then the machine C has the following form:

(ii) By assumption, we are given two automata A and B such that

(A)=

and

(B)=

. Construct the

following ε-automaton: from each terminal state of A draw an

-transition to the initial state of B. Make

each of the terminal states of A ordinary states and make the initial state of B an ordinary state. Call

the resulting automaton C. It is easy to see that this

-automaton recognises

. We now apply

Theorem 4.1.2 to obtain a non-deterministic

< previous page page_91 next page >

< previous page page_92 next page >

Page 92

automaton recognising

. Thus

is recognisable. If we picture A and B schematically as above then

the machine C has the following form:

(iii) Let A be a deterministic automaton such that

(A)=

. Construct an

-automaton D as follows. It

has two more states than A, which we shall label and ♠: the former will be initial and the latter

terminal. Connect the state

by an

-transition to the initial state of A and then make the initial state

of A an ordinary state. Connect all terminal states of A to the state labelled ♠ and then make all terminal

states of A ordinary states. Connect the state

by an

-transition to the state ♠ and vice versa. If we

picture A schematically as above, then D can be pictured schematically as follows:

It is easy to check that

(B)=

first, by construction,

is recognised. Second, the bottom

-transition

enables us to re-enter the machine A embedded in the diagram. The result now follows by Theorem

4.1.2 again.

To motivate our next results, consider the following question: is the language {0

≥0}

recognisable? We know that the answer is no because we proved that the language {

anbn: n

≥0} is not

recognisable and the only difference between these two languages is that we have replaced

by 0 and

by 1. We can similarly see that the language {(011)

(10)

≥0} is not recognisable; this time we

have replaced

by 011 and

by 10. We need to be

< previous page page_92 next page >

< previous page page_93 next page >

Page 93

able to prove these assertions and, in doing so, we will develop a powerful way of comparing different

languages. Let

and

be two alphabets, not necessarily different. A function

α: A

*→

* is said to be a

monoid homomorphism

if it satisfies two conditions:

(MM1)

α(ε)

(MM2)

α(xy)

α(x)α(y)

for all strings .

Although the definition is a little complex, it turns out to be very easy to define monoid

homomorphisms. To see why, let Using (MM2) repeatedly we see that

In other words, once we know the values of a(a) for

each letter

then we can compute the value

α(x)

for

any string

. In fact, something stronger is true. Let

α′: A

→

* be any function with no

restrictions placed on

α′

. Then we can define a monoid homomorphism

from

* to

* as follows: we

put

α(ε)

because we have no choice; if

…an

is an arbitrary non-empty string, then define

It is easy to check that

is a monoid homomorphism. It follows that to define a monoid homomorphism

we need only define

on the letters in

Example 4.2.2 Let

={0, 1} and

{a, b}

. Define

α: A

*→

* by putting

(0)=

and

(1)=

. Then

we can easily compute

(000111) as follows:

Monoid homomorphisms enable us to compare languages over different alphabets. To see how, let

α:

*→

* be a monoid homomorphism, and let . Define

the

image of L under α

. Clearly

α(L)

is a language over the alphabet

Theorem 4.2.3

Let α: A

*→

be a monoid homomorphism, and let be recognisable

Then

is recognisable.

Proof Let A be a deterministic automaton that recognises

. We shall construct an automaton B from A,

which recognises

α(L)

. In general, B will be an

-automaton. The states of B will consist of the states of

A together with possibly some extra states. For each

and for each transition

q′,

carry out the

following procedure. Suppose that

α(a)

…bn

where ;

< previous page page_93 next page >

< previous page page_94 next page >

Page 94

we allow the possibility that

α(a)

is the empty-string. Then construct the sequence of transitions in B:

Here

,…, sn

−1 are

n−

1 new states. Finally, the initial state of B is the same as the initial state of A

and the terminal states of B are the same as the terminal states of A. It is now easy to check that the

language recognised by the non-deterministic

-automaton B is precisely

α(L)

Let

α: A

*→

* be a monoid morphism. For each define

the

inverse image of L under α

. Clearly

−1

(L)

is a language over the alphabet

Theorem 4.2.4

Let α: A

*→

be a monoid homomorphism

recognisable then α

−1

(L) is

recognisable

Proof Let B=

(S, B, i, δ, T)

be a deterministic automaton recognising

. We construct a deterministic

automaton A recognising

−1

(L)

as follows. The set of states of A is the same as the set of states of B;

likewise the initial and terminal states. The difference between A and B lies in the transition function,

which we denote by

. This is defined as follows. For each

and for each state define

By construction A is deterministic. It is easy to check that

It follows that

Hence

−1

(L)

is recognisable as claimed.

Here is one application of our results on monoid homomorphisms.

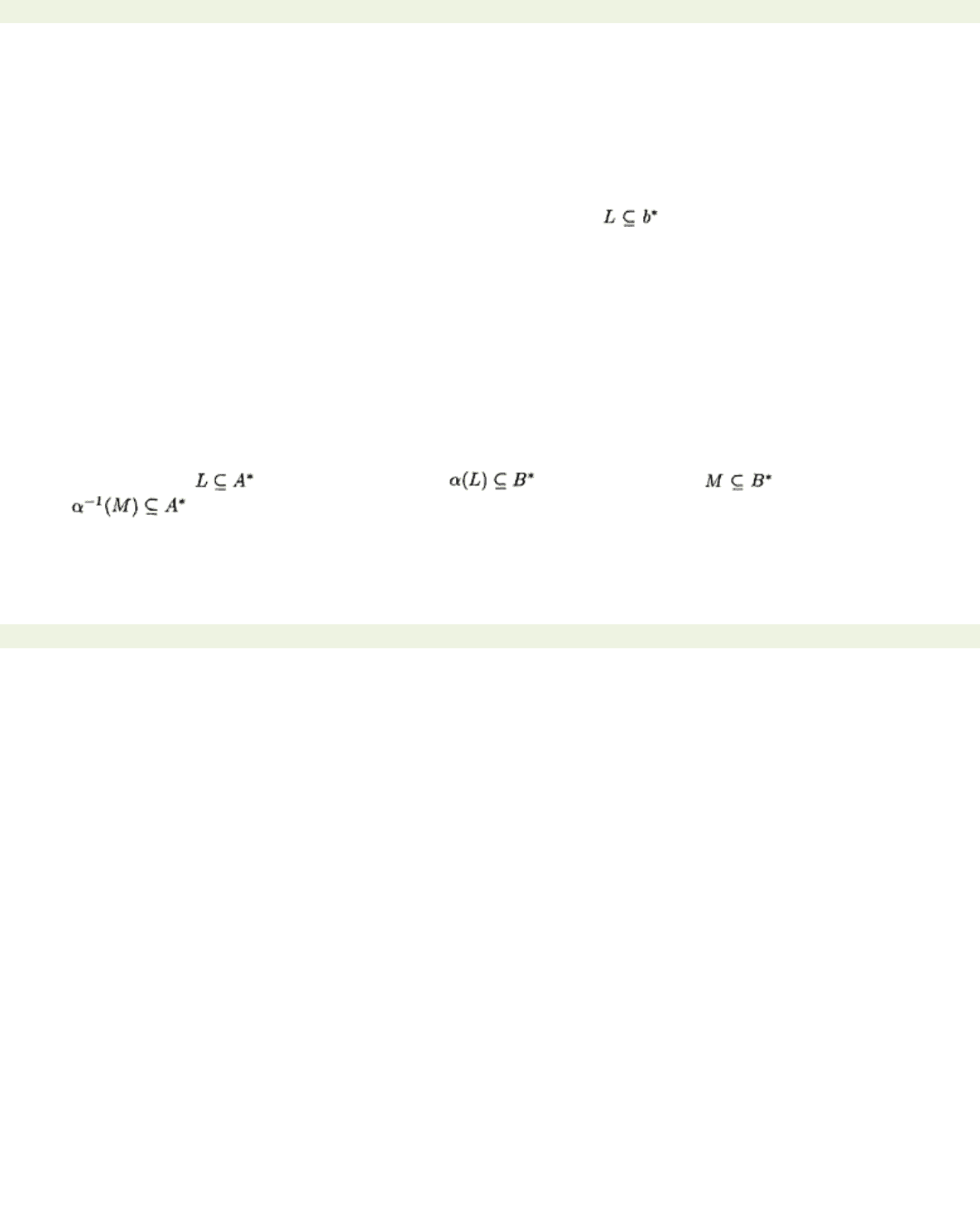
Example 4.2.5 The language

aibjci

j: i, j

≥0} is not recognisable. To prove this, let

{a, b, c}

and

{b, c}

. Define

α: A

*→

* by

α(a)

ε, α(b)

and

α(c)

. The image of

under this monoid

homomorphism is

bkcl: l

≥

≥0}. If

is recognisable then so is

. But we can show using the

Pumping Lemma that

is not recognisable. It follows that

is not recognisable.

< previous page page_94 next page >

< previous page page_95 next page >

Page 95

Exercises 4.2

1. Construct

-automata to recognise each of the followings languages:

(i)

)

(ii)

(a(ab)

(iii) (

*)(

2. Complete the proof of Theorem 4.2.3.

3. Complete the proof of Theorem 4.2.4.

4. This question follows on from Question 3 of Exercises 2.6. Let be an arbitrary non-recognisable

language. Put

*. Using Theorem 4.2.3, prove that

is not recognisable.

This example is taken from [136].

4.3 Summary of Chapter 4

•

ε-automata:

These are defined just as non-deterministic automata except that we also allow

transitions to be labelled by

. A string

over the input alphabet is accepted by such a machine A if

there is at least one path in A starting at an initial state and finishing at a terminal state such that when

the labels on this path are concatenated the string

is obtained.

• A

: There is an algorithm that converts an

-automaton A into a non-deterministic automaton A

recognising the same language. The ‘s’ stands for ‘sans’ meaning ‘without (epsilons).’

•

Applications:

Using

-automata, simple proofs can be given of the recognisability of

from the

recognisability of

and

and the recognisability of

* from the recognisability of

•

Monoid homomorphisms:

A function

α: A

*→

* is a monoid homomorphism if

α(ε)

and

α(xy)

α(x)α(y)

. If is recognisable, then is recognisable. If is recognisable,

then

is recognisable.

4.4 Remarks on Chapter 4

The constructions of Theorem 4.2.1 are usually attributed to [86]. The closure of recognisable languages

under monoid homomorphisms is a special case of [9], whereas the closure under inverse images is from

[53].

< previous page page_95 next page >

< previous page page_96 next page >

Page 96

It is interesting to compare the proofs of Theorems 4.2.3 and 4.2.4. In showing that the image of a

recognisable language is recognisable, we had to use ε-automata because the image of a letter could be

the empty string. Contrast this with the proof that the inverse image of a recognisable language is

recognisable; here we could get away with using complete deterministic automata. In some sense,

forming the inverse image of a recognisable language seems to be a more natural operation than taking

its image. This idea will re-emerge in Chapter 12, when I come to describe Varieties of languages.’

< previous page page_96 next page >