Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_67 next page >

Page 67

2. Find a non-deterministic automaton with 4 states that recognises the language (0+1)*1(0+1)2. Use

the accessible subset construction to find a deterministic automaton that recognises the same language.

3. Let

≥1. Show that the language (0+1)*1(0+1)

−1 can be recognised by a non-deterministic

automaton with

+1 states. Show that any deterministic automaton that recognises this language must

have at least 2

states.

This example shows that an exponential increase in the number of states in passing from a non-

deterministic automaton to a corresponding deterministic automaton is sometimes unavoidable.

3.3 Applications

Non-deterministic automata make designing certain kinds of automata easy: we may often simply write

down a non-deterministic automaton and then apply the accessible subset construction. It is however

worth pointing out that the automata obtained by applying the accessible subset construction will often

have some rather obvious redundancies and can be simplified further. The general procedure for doing

this will be described in Chapter 7.

In this section, we look at some applications of non-deterministic automata. Our first result generalises

Example 3.2.1.

Proposition 3.3.1

Let L be recognisable. Then rev(L), the reverse of L, is recognisable.

Proof Let

(A), where A=

(S, A, I, δ, T)

is a non-deterministic automaton. Define another non-

deterministic automaton Arev as follows:

where

is defined by if and only if

;

in other words, we reverse the arrows of A

and relabel the initial states as terminal and vice versa. It is now straightforward to check that

if and only if . Thus

(Arev)=rev

(L)

The automaton Arev is called the

reverse

of A.

Non-deterministic automata provide a simple alternative proof to Proposition 2.5.6.

Proposition 3.3.2

Let L and M be recognisable. Then L+M is recognisable.

Proof Let A and B be non-deterministic automata, recognising

and

respectively. Lay them side by

side; the result is a non-deterministic automaton recognising

< previous page page_67 next page >

< previous page page_68 next page >

Page 68

In Section 2.4, we considered the recognisability of languages defined in terms of the presence of

patterns of various kinds. The following result shows how easy the proofs become in this case when we

use non-deterministic automata.

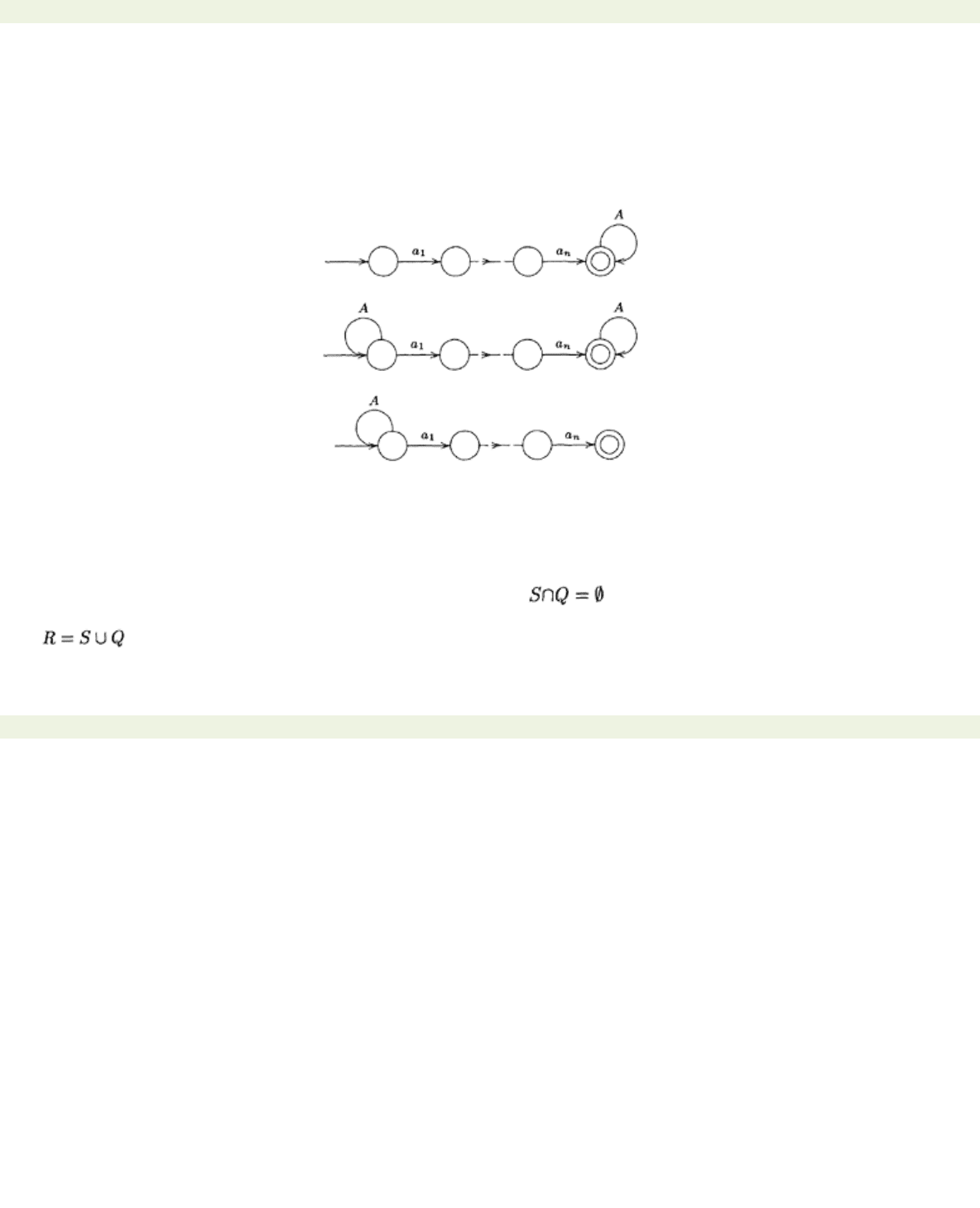
Proposition 3.3.3

Let A be an alphabet and let w

…anbe a non-empty string over A

Each of the

languages wA

, A

and A

w is recognisable

Proof Each language can be recognised by the respective non-deterministic automaton below, which I

have drawn schematically:

and

Each of these can be converted into an equivalent deterministic automaton using the accessible subset

construction.

In Chapter 1 we introduced the product of two languages and the Kleene star of a language.

Proposition 3.3.4

If L and M are recognisable, then LM is recognisable.

Proof Let A=

(S, A, S

, δ, F)

and B=

(Q, A, Q

, γ, G)

be non-deterministic automata, recognising

and

respectively. We shall combine these two automata into a new, non-deterministic automaton C such

that

(C)=

. It is no loss in generality to assume that . We define C=

(R, A, R

, ξ, H)

follows:

•

;

the set of states of the new machine is the union of the sets of states of the two original

machines.

•

;

the set of initial states of the new machine is just the set of initial states of A.

< previous page page_68 next page >

< previous page page_69 next page >

Page 69

•

the set of terminal states is if one of the initial states of B is also terminal, otherwise the set

of terminal states is just

the set of terminal states of B.

• Transition function

ξ:

all the transitions in A are carried forward to C as are all the transitions in B; we

also introduce new transitions from the states in

to the states in

0·

. We do this as follows: for each

and for each transition in B where add the transition to

in C. A picture

of this may be helpful.

The automaton C is a well-defined, non-deterministic automaton. We show that

(C)=

First we prove that . Let . There are two possibilities. If

then either

labels

a path in C from a state in

0 to a state in

labels a path in C from a state in

0 to a state in

whereas if then only the second case can occur. In the first case, and so .

In the second case,

must traverse one of the new transitions. Thus

uav,

where

, ,

and

where . By construction, . It follows that . Thus

Hence .

To prove the reverse inclusion, let

. There are two possibilities: if

then either or

where

and

≠

ε,

whereas if

then only the second case can occur. In the first

case, . In the second case, we can write

where

is, by assumption, non-empty. Thus

for some and . We can now essentially reverse our argument from the first part of

the proof above to get .

The new transitions in C can be described as follows: for each state in

copy the transitions out of the

states in

0 in B.

Example 3.3.5 Let

and let

An automaton A that recognises

< previous page page_69 next page >

< previous page page_70 next page >

Page 70

and an automaton B that recognises

Using the construction in Proposition 3.3.4, an automaton C that recognises

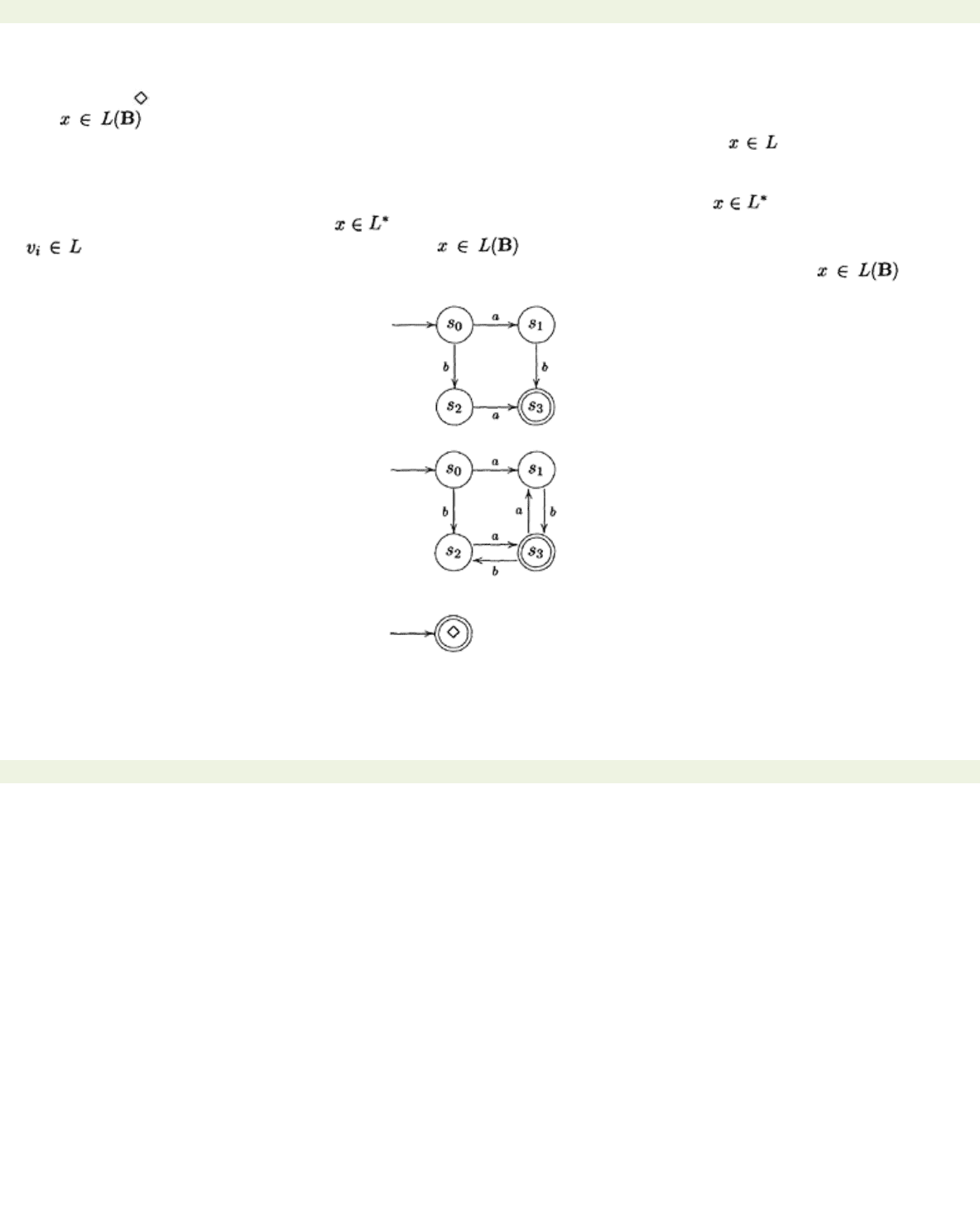
Proposition 3.3.6

If L is recognisable, then L

is recognisable.

Proof Let A=

(S, A, S

, δ, F)

be a non-deterministic automaton such that

(A)=

. We construct a new

non-deterministic automaton,

as follows:

• The set of states

is just the set

together with a new state .

• The set of initial states

0 is just the set of initial states

0 together with .

• The set of terminal states

is the set of terminal states

together with .

• The transition function

γ:

all the transitions in A are carried forward; we also introduce new transitions

from states in

to states in

0·

. We do this as follows: for each state and each transition

where add the transition to

in B. A picture of this may be helpful.

< previous page page_70 next page >

< previous page page_71 next page >

Page 71

It is clear that B is a well-defined, non-deterministic automaton. We prove that

(B)=

*. The only role

of the state is to recognise

. So in what follows we can limit ourselves to non-empty strings.

Let . Then there is a path in B, which I shall call ‘successful,’ starting at a state in

0 and

ending at a state in

labelled by

. If

uses none of the new transitions, then . Otherwise we can

factor

…un,

where the symbols

, a

…

are the labels of the new transitions occurring in

the successful path. From the definition of the new transitions, this implies that each of the strings

u1,

),…, (an−

un)

is accepted by

(A) and so belongs to

. It follows that .

To prove the reverse inclusion, let

be a non-empty string. We can factorise

…vn

where each

and is non

empty. If

=1, then clearly . Assume

≥2. We can write each

aiui

for

≥2. We can now essentially reverse our argument from the first part of the proof to get .

Example 3.3.7 Let

{ab, ba}

. An incomplete automaton A recognising

Using the construction of Proposition 3.3.6, an automaton B recognising

* is

Exercises 3.3

1. Construct non-deterministic automata recognising the following languages over the alphabet

{a,

(i) (

2)(

)*.

< previous page page_71 next page >

< previous page page_72 next page >

Page 72

(ii) (

)*(

2).

(iii) (

)*(

aaa

bbb

)(

)*.

(iv) (

ba+b

)*.

(v) ((

2)*

))*.

2. Construct an incomplete automaton A=

(S, A, i, δ, T)

such that the automaton B=

(S, A, i, δ, S\T)

does not recognise

(A)′, the complement of

(A).

It is only possible to prove that the complement of a recognisable language is recognisable using

complete deterministic automata.

3.4 Trim automata

We defined the idea of an accessible automaton for complete deterministic automata in Section 3.1. We

now extend the definition to arbitrary non-deterministic automata.

Notation Let

be a non-deterministic automaton. If

and then we define

the set of all states that can be reached starting in

and following paths labelled

. If then we

define

the set of all states that can be reached starting in

and following paths labelled by elements of

Using this notation, the language

(A) recognised by A is simply

Let A be a non-deterministic automaton with state set

and input alphabet

. We say that a state

accessible

if there is some string

which labels a path from one of the initial states to

An automaton A is

accessible

if every state is accessible. The set of accessible states is

*. It follows

that any states of A that are not in

* can play no role in accepting or rejecting a string and can

therefore be removed. Put

< previous page page_72 next page >

< previous page page_73 next page >

Page 73

and let

δa

be the restriction of

. Put A

(Sa, A, I, δa, Ta)

. In other words, the automaton

is constructed by erasing all non-accessible states and any transitions to or from them. It is clear

that

(A)=

). We call A

the

accessible part

of A. We already have an algorithm that computes the

set

Sa;

this is the ‘accessible subset construction’ of Section 3.1. Apply this algorithm to A, and the

states that occur as labels of the vertices in this algorithm are precisely the accessible states.

We now define a notion dual1 to that of accessibility. Let A be a non-deterministic automaton with state

set

and input alphabet

. A state

coaccessible

if there is a string such that

contains a

terminal state. We say A is

coaccessible

if every state is coaccessible. The algorithm for finding the

coaccessible states is simply a variant of the one for finding the accessible states. Notice that A is

coaccessible

if and only if Arev, the reverse of A, is accessible. Thus to calculate the coaccessible states

of A, it is enough to calculate the accessible states of Arev. The

coaccessible part

of A, denoted A

, is

defined in the same way as A

except that the states of A

are the coaccessible states of A. Clearly

(A).

An automaton is

trim

if it is both accessible and coaccessible. A trim automaton is therefore one in

which for each state

there is an initial state

s′

and a string

such that

and a string

and a

terminal state

such that

;

that is, in a trim automaton each state occurs on some path from an

initial state to a terminal state. For every automaton A the automata A

and A

are the same and

both are trim. See Exercises 3.4. We denote this common automaton by A

, called the

trim part of

Clearly,

(A)=

). We state this result formally as follows.

Proposition 3.4.1

Each recognisable language is recognised by a trim automaton.

It is straightforward to construct the trim part of an automaton. However, there is one point where the

reader has to be wary. The following example illustrates the difficulty.

Example 3.4.2 Consider the complete deterministic automaton A given by

1This is a useful term common in mathematics. It is applied in situations where there are exactly two

ways of progressing; for example, we might have a choice between left or right or, as here, between

initial and terminal, If we choose one of the pair, then the other is the ‘dual.’ Here we have a choice

between initial states and terminal states; accessibility was defined in terms of the initial states so the

dual is defined in terms of the terminal states. The prefix ‘co’ is often prefixed to a word to denote the

dual form if there is no other word readily available.

< previous page page_73 next page >

< previous page page_74 next page >

Page 74

This automaton is already accessible but it is not coaccessible because there is no path from the state 3

to the terminal state. In this case, therefore, A

is just

This example shows that a complete automaton may become incomplete when the coaccessible part is

taken.

Accessibility and coaccessibility can be put to work to solve problems. We begin with three decision

problems. The first is: given a non-deterministic automaton A is

(A) empty?

Proposition 3.4.3

Let

be a non-deterministic automaton

Then if and only if

t is empty

Proof If A

is empty then the result is immediate. Suppose now that the language

(A) is empty and

that A

is not. Then any state in A

is part of a path from an initial state to a terminal state in A. Such a

path would be labelled by a string in

that would therefore belong to

(A) by definition. Thus if

(A)

is empty then A

is empty.

If a language is not empty we want to know whether it is finite or infinite. Again this can easily be

answered. By a

closed path

in an automaton we mean a path that begins and ends at the same state.

The

length

of the path is the number of edges used.

Proposition 3.4.4

Let

be a non-deterministic automaton. Then L

(A)

is finite and non-empty if and

only if

t is non-empty and does not contain a closed path of length at least 1

Proof Suppose that

(A) is finite and non-empty. Then by Proposition 3.4.3, we know that A

is non-

empty. Suppose A

contained a closed path begining and ending at the vertex

. Let be the non-

empty string that labels the edges on this path. Since A

is trim there is a string

such that

s′

where

s′

is an initial state. Likewise there is a string

such that

where

t i

s a terminal state. Thus

the string

. However, by traversing the closed path an arbitrary number of

times. It follows that

) is infinite, which is a contradiction. Thus A

contains no closed paths of

length 1 or more.

To prove the converse, suppose that

is non-empty and contains no closed paths. We prove that

) is finite. Suppose not. Let A

have

states. Because

) is infinite we can find a string

such that |

|≥

. By the same argument we used in proving the Pumping Lemma (Section

2.6), the path in A

labelled by

must contain a repeated vertex. Thus A

must contain a closed path,

which is a contradiction. It follows that

) is finite.

We can also use trim automata to compare the languages accepted by two different automata.

< previous page page_74 next page >

< previous page page_75 next page >

Page 75

Proposition 3.4.5

Given two complete deterministic automata

and

it is decidable whether

(A)=

(B).

Proof Let

(A) and

(B). By simple set theory,

if and only if . We now

use the constructions of Section 2.5. Construct the automaton C=A′×B. Then

(C)=

L′

Similarly, we may construct an automaton D such that

(D)=

. Finally, we may construct an

automaton E such that

(E)=

(C)+

(D). By Proposition 3.4.3, it follows that

if and only if E

empty.

For each language

we may define the following languages: Prefix

(L),

Suffix

(L),

and Factor

(L)

which are, respectively, the prefixes of elements of

the suffixes of elements of

and the factors of

elements of

Proposition 3.4.6

Let L be a recognisable language. Then each of

Prefix

(L),

Suffix

(L), and

Factor

(L) is

recognisable

Proof We show first that Prefix

(L)

is recognisable. Let A=

(S, A, I, δ, T)

be a coaccessible automaton

that recognises

. Consider the automaton

We show that

(B)=Prefix

(L)

. Let . Then

labels a path in B, which starts at some initial state

and ends at a state

that is, . It follows that

labels a path from

in A. By assumption,

A is coaccessible and so there is a such that

contains a terminal state. Hence and

so . Conversely, suppose that . Then there exists such that .

But then is immediate.

To show that Suffix

(L)

is recognisable, let A=

(S, A, I, δ, T)

be an accessible automaton that recognises

. Consider the automaton

We show that

(C)=Suffix

(L)

. Let . Then there is some state such that

contains a

terminal state

. Now

labels a path in A from

. By assumption A is accessible, and so there is a

string

from an initial state

s′

such that

labels a path from

s′

. Thus

labels a path from an

initial state of A to a terminal state of A. Hence . Thus . Conversely, suppose that

. By definition there exists a string

such that . It is now immediate that .

Finally, to show that Factor

(L)

is recognisable, let A=

(S, A, I, δ, T)

be a trim automaton that recognises

. Consider the automaton

We leave it as an exercise to check that

(D)=Factor

(L)

< previous page page_75 next page >

< previous page page_76 next page >

Page 76

Exercises 3.4

1. Show that for each automaton A we have that A

2. Complete the proof of Proposition 3.4.6, and prove that if L is recognisable, then Factor

(L)

recognisable.

3.5 Grammars

Automata are devices for recognising strings belonging to a language. In this section, we introduce

grammars that are devices for

generating

strings belonging to a language. We shall then use non-

deterministic automata to show how to convert from automata to certain types of grammars and back

again. We do not use grammars anywhere else in this book.

The motivation for the concept of a grammar comes from linguistics. Learning a language involves many

different skills, however, at its most simplistic, we have to learn two things: the vocabulary of the

language and the rules for combining the words in the vocabulary. These rules are usually couched in

terms of words such as ‘nouns,’ ‘adjectives,’ ‘verbs,’ and so on. For example, we learn that in French

most adjectives follow the noun they modify, whereas in German adjectives precede nouns. To expand

on this we give a very simple grammar for a small portion of English.

Example 3.5.1 Consider the following fragment of English. Phrases in English can be classified

according to the grammatical categories to which they belong. We shall use only the following:

•

Sentence

denoted by S.

•

Noun-phrase

denoted by NP.

•

Verb-phrase

denoted by VP.

•

Noun

denoted by N.

•

Definite article

denoted by T.

•

Verb

denoted by V.

In addition, there are rules that tell us how the grammatical categories are related to each other. We

shall use an arrow → to indicate how a grammatical category on the left can be constructed from

grammatical categories on the right; I have used the symbol · for concatenation for the sake of clarity:

(1) S→NP·VP.

(2) NP→T·N.

< previous page page_76 next page >