Лазарев Ю.Ф. Mатематическое моделирование физических процессов и технических систем в MATLAB
Подождите немного. Документ загружается.


231
s^2 + 10 s + 100
Параллельное соединение этих двух контуров управление можно осуществить тоже двумя путями: либо
используя процедуру
parallel
Izm1=parallel(GN,GT)
Transfer function:
2 s^2 + 120 s + 200
-------------------
s^2 + 10 s + 100
либо применяя операцию «сложения» моделей
Izm = GN+GT
Transfer function:
2 s^2 + 120 s + 200
-------------------
s^2 + 10 s + 100
Теперь найдем модель всей системы автоматического управления угловым движением торпеды, рассматривая
цепь управления как цепь отрицательной обратной связи для торпеды и пользуясь для объединения прямой и
обратной цепи процедурой
feedback:
sys=feedback(Tor,Izm)
Transfer function:
25 s^2 + 250 s + 2500
----------------------------------------------
100 s^4 + 1050 s^3 + 10550 s^2 + 8000 s + 5000
Конечно, несравненно более простым и удобным средством «создания» (точнее – «набора») сложных систем
из отдельных блоков является рассмотренная в главе 7 интерактивная система SIMULINK.
После того как система сформирована, можно ввести при помощи процедуры set некоторые символьные ее
описания. В частности, дать названия входам и выходам системы, дать краткий комментарий к самой системе,
например:
set(sys,'InputName',' Момент сил','OutputName','Угол рыскания')
set(sys,'Notes','Угловое движение торпеды')
get(sys)
num = {[0 0 25 250 2.5e+003]}
den = {[100 1.05e+003 1.06e+004 8e+003 5e+003]}
Variable = 's'
Ts = 0
InputName = {' Момент сил'}
OutputName = {'Угол рыскания'}
Notes = {'Угловое движение торпеды'}
UserData = []
В заключение приведем примеры использования процедур конкатенации:
sysvsp1=horzcat(Torsk,SkUg)
Transfer function from input 1 to output:
25
----------
100 s + 50
Transfer function from input 2 to output:
1
-
s
sysvsp2=vertcat(Torsk,SkUg)
Transfer function from input to output...
25
#1: ----------
100 s + 50
232
1
#2: -
s
6.3. Получение информации о модели
Чтобы получить отдельные характеристики (матрицы и векторы, описывающие пространство состояния,
коэффициенты числителя и знаменателя передаточной функции и т. п.) полученной модели, можно
использовать одну из следующих процедур:
- tfdata (для получения векторов числителя и знаменателя передаточной функции системы),
- ssdata (для получения значений матриц уравнений пространства состояния)
- zpkdata (для получения векторов значений полюсов и нулей системы).
Например:
[nom,den]=tfdata(sys,'v')
nom = 0 0 25 250 2500
den =
sssys=ss(sys);
100 1050 10550 8000 5000
[A,B,C,D] = ssdata(sssys)
A =
-10.5 -6.5938 -0.625 -0.048828
16 0 0 0
0 8 0 0
0 0 8 0
B =
0.25
0
0
0
C =
0 0.0625 0.078125 0.097656
D =
0
[z,p,k] = zpkdata(sys,'v')
z =
-5 + 8.6603i
-5 - 8.6603i
p =
-4.8653 + 8.5924i
-4.8653 - 8.5924i
-0.38466 + 0.60403i
-0.38466 - 0.60403i
k =
0.25
Процедура get дает возможность получить полную характеристику модели, включая имена входов и выходов,
примечания, значения шага дискретизации и т. п. Например:
get(sys)
233
num: {[0 0 25 250 2.5e+003]}
den: {[100 1.05e+003 1.06e+004 8e+003 5e+003]}
Variable: 's'
Ts: 0
ioDelay: 0
InputDelay: 0
OutputDelay: 0
InputName: {' Момент сил'}
OutputName: {'Угол рыскания'}
InputGroup: {0x2 cell}
OutputGroup: {0x2 cell}
Notes: {'Угловое движение торпеды'}
UserData: []
Continuous-time system.
get(sssys)
a: [4x4 double]
b: [4x1 double]
c: [0 0.0625 0.0781 0.0977]
d: 0
e: []
StateName: {4x1 cell}
Ts: 0
ioDelay: 0
InputDelay: 0
OutputDelay: 0
InputName: {' Момент сил'}
OutputName: {'Угол рыскания'}
InputGroup: {0x2 cell}
OutputGroup: {0x2 cell}
Notes: {'Угловое движение торпеды'}
UserData: []
О числе входов и выходов системы можно узнать, обратившись к процедуре size:
size(sys)
Transfer function with 1 input(s) and 1 output(s).
size(ssys)
State-space model with 1 input(s), 1 output(s), and 4 state(s).
6.4. Анализ системы
Пакет СONTROL предоставляет широкий набор процедур, осуществляющих анализ САУ с самых различных
точек зрения и, прежде всего, определение откликов системы на внешние воздействия как во временной, так и в
частотной областях.
Для нахождения временных откликов системы на внешние воздействия некоторых видов предусмотрены
функции:
- impulse - нахождение отклика системы на единичное импульсное входное воздействие;
- step - нахождение реакции системы на единичный скачок входного воздействия;
- initial - определение собственного движения системы при произвольных начальных условиях;
- lsim -
определение реакции системы на входное воздействие произвольной формы, задаваемое
в виде вектора его значений во временит.
Рассмотрим применение этих процедур на примере движения торпеды, параметры которой как САУ приведены
ранее.
Применяя процедуру
step к созданной модели:
step(sys), grid
можно получить график, представленный на рис. 6.1.
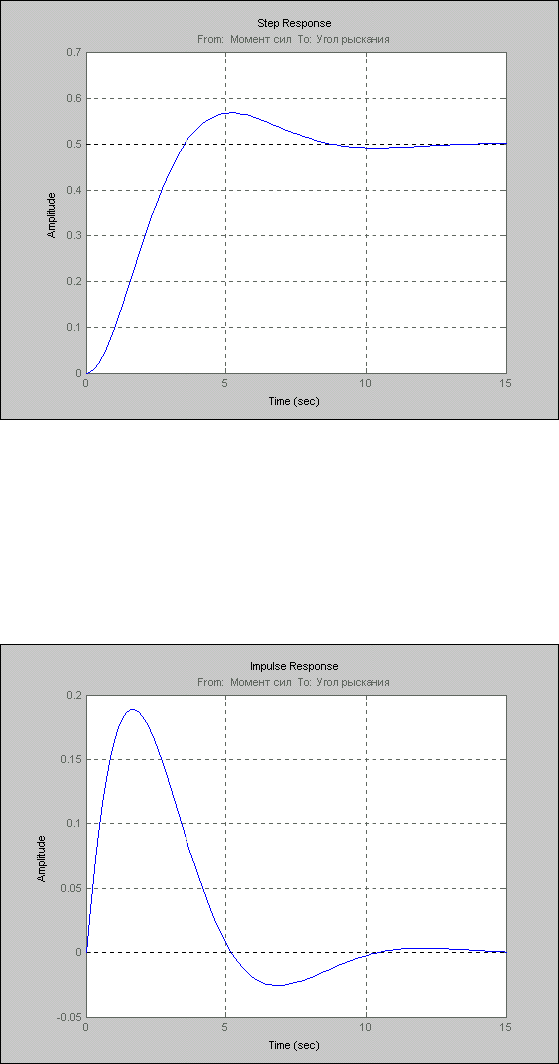
234
Рис. 6. 1. Отклик системы SYS на единичное ступенчатое воздействие
Аналогично, использование процедуры
impulse(sys), grid
приведет к появлению в графическом окне графика рис. 6.2.
Рис. 6. 2. Отклик системы SYS на единичное импульсное воздействие
Чтобы применить процедуру
initial
, необходимо в число входных параметров включить, во-первых,
полный вектор всех начальных условий по переменным состояния, а во-вторых, момент времени окончания
процесса интегрирования. Например:
initial(sssys,[0 0 0 1],20), grid
Получим в графическом окне картину, показанную на рис. 6.3.
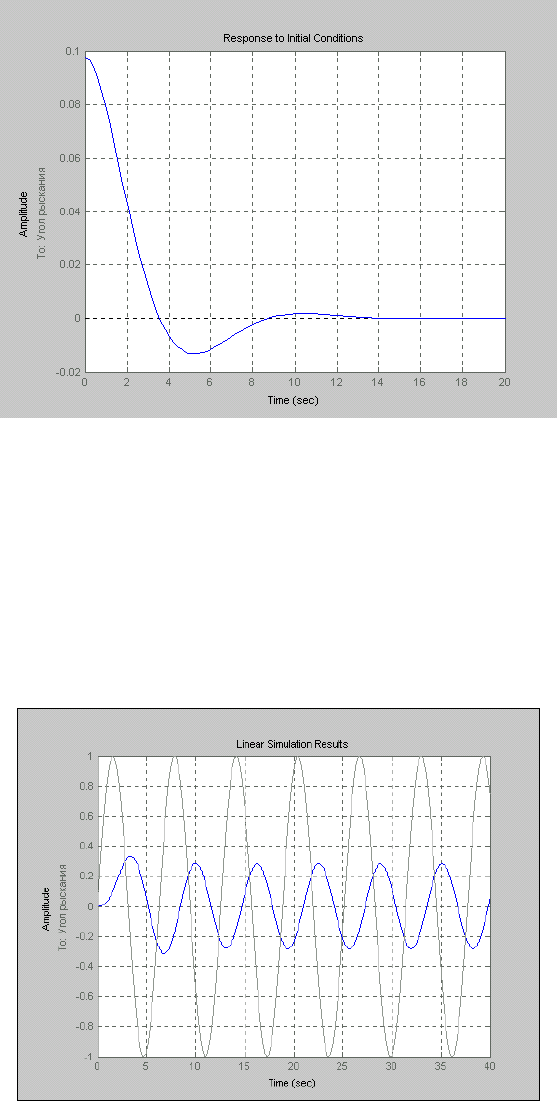
235
Рис. 6. 3. Переходный процесс в системе SSSYS при заданных начальных условиях
Для применения процедуры
lsim необходимо предварительно задать вектор 't' значений времени, в которых
будут заданы значения входного воздействия, а затем и задать соответствующий вектор 'u' значений входной
величины в указанные моменты времени
t = 0:0.01:40; u = sin(t); lsim(sssys,u,t);grid
Результат изображен на рис. 6.4. На нем одна кривая отображает входное воздействие, а другая – реакцию на
него системы.
Рис. 6. 4. Реакция системы SSSYS на заданное воздействие
Следующая группа процедур представляет в частотной области реакцию системы на внешние гармонические
воздействия. К таким процедурам относятся:
- bode - строит графики АЧХ и ФЧХ (диаграмму Боде) указанной системы;
- nyquist - строит в комплексной плоскости график Амплитудно-Фазовой Характеристики (АФХ)
системы в полярных координатах;
- nichols - строит карту Николса системы, т. е. график АФХ разомкнутой системы в декартовых
координатах;
- sigma - строит графики зависимости от частоты сингулярных значений системы; обычно совпадает с
АЧХ системы;
236
- margin -
строит диаграмму Боде с указанием
запасов по амплитуде и по фазе.
Приведем примеры.
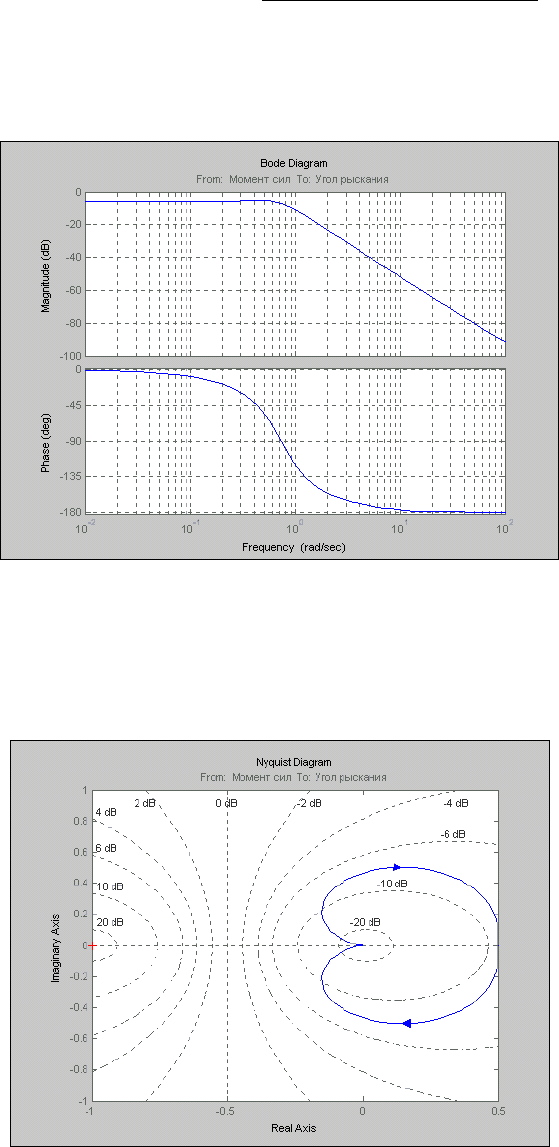
bode(sys), grid
- результат приведен на рис. 6.5;
Рис. 6. 5. Диаграммы Боде (АЧХ и ФЧХ) системы SYS
nyquist(sys); grid
-
результат - на рис. 6.6;
Рис. 6. 6. Диаграмма Найквиста системы SYS
nichols(sys); grid
-
результат показан на рис. 6.7;
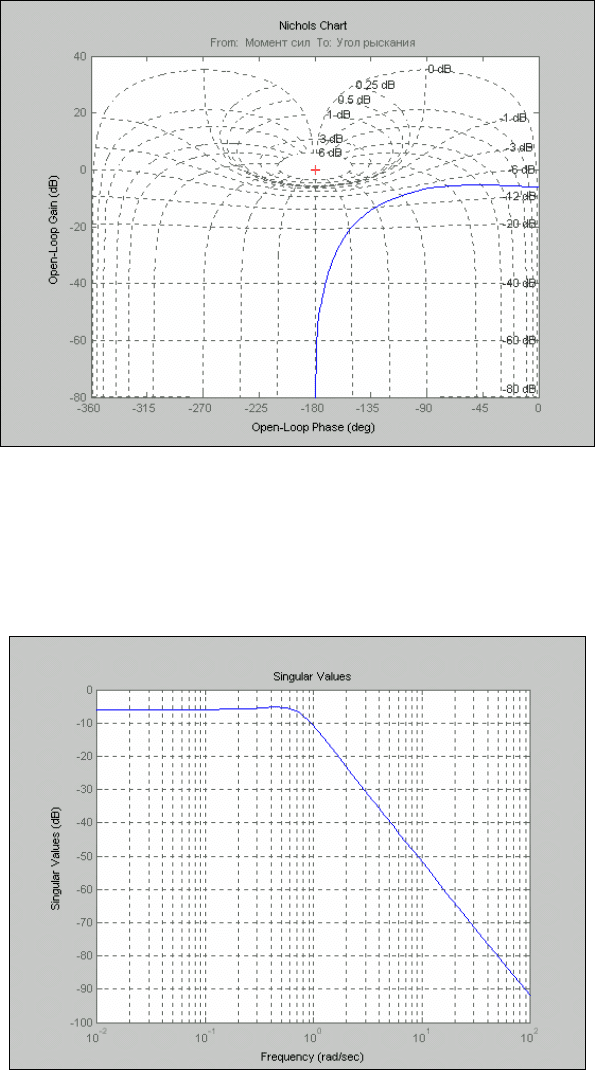
237
Рис. 6. 7. Карта Николса для разомкнутой системы SYS
sigma(sys), grid
-
см. рис. 6.8;
Рис. 6. 8. Частотная зависимость сингулярных чисел системы SYS
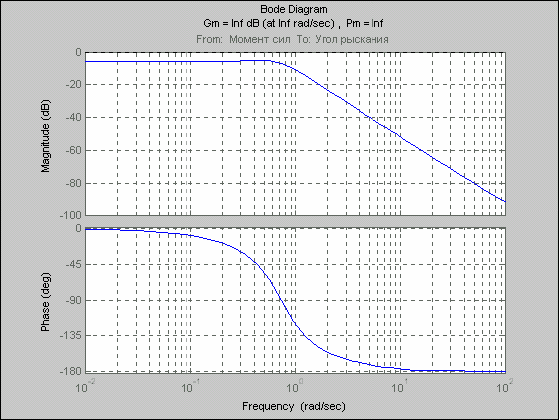
margin(sssys); grid
-
см. рис. 6.9.
238
Рис. 6. 9. АЧХ и ФЧХ системы SYS с указанием запасов по амплитуде и фазе
Теперь рассмотрим процедуры, вычисляющие отдельные характеристики и графически показывающие
расположение полюсов и нулей системы. К ним можно отнести
- pole - расчет полюсов системы;
- zpkdata - расчет полюсов, нулей и коэффициента передачи системы;
- gram - вычисление граммианов системы - матрицы управляемости (при указании в качестве
последнего входного параметра процедуры флага 'c') и матрицы наблюдаемости системы (при
указании флага 'o');
- damp - вычисление собственных значений матрицы состояния системы и, на этой основе -
значений собственных частот (Frequency) незатухающих колебаний системы и относительных
коэффициентов демпфирования (Damping)
- pzmap - построение на комплексной плоскости карты расположения нулей и полюсов системы
- rlocus - расчет и вывод в виде графиков в графическое окно траектории движения на
комплексной плоскости корней полинома
H(s) = D(s) + k * N(s) = 0,
где D(s) - знаменатель передаточной функции, N(s) - ее числитель, при изменении положительного
вещественного числа k от 0 до бесконечности.
Далее приводятся примеры применения этих функций и результаты:
pole(sys)
ans =
-4.8653 + 8.5924i
-4.8653 - 8.5924i
-0.3847 + 0.6040i
-0.3847 - 0.6040i
sysz=zpk(sys)
Zero/pole/gain from input " Момент сил" to output "Угол рыскания":
0.25 (s^2 + 10s + 100)
------------------------------------------------
(s^2 + 0.7693s + 0.5128) (s^2 + 9.731s + 97.5)
[z,p,k]=zpkdata(sysz,'v')
z =
239
-5.0000 + 8.6603i
-5.0000 - 8.6603i
p =
-4.8653 + 8.5924i
-4.8653 - 8.5924i
-0.3847 + 0.6040i
-0.3847 - 0.6040i
k =
0.2500
Wc= gram(sssys,'c')
Wc =
0.0032245 1.3753e-016 -0.0041717 -1.5179e-015
1.3753e-016 0.0083434 -1.4832e-016 -0.070084
-0.0041717 -1.4832e-016 0.070084 -7.7542e-016
-1.5179e-015 -0.070084 -7.7542e-016 8.7807
Wo=gram(sssys,'o')
Wo =
1.3335 0.8751 1.0938 0.0977
0.8751 0.5770 0.7210 0.0682
1.0938 0.7210 0.9011 0.0851
0.0977 0.0682 0.0851 0.0134
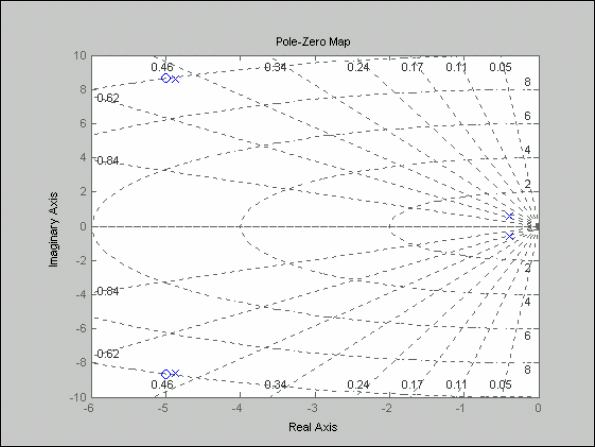
pzmap(sys), grid
-
результат см. рис. 6.10
Рис. 6. 10. Изображение нулей и полюсов системы SYS
damp(sys)
Eigenvalue Damping Freq. (rad/s)
240
-3.85e-001 + 6.04e-001i 5.37e-001 7.16e-001
-3.85e-001 - 6.04e-001i 5.37e-001 7.16e-001
-4.87e+000 + 8.59e+000i 4.93e-001 9.87e+000
-4.87e+000 - 8.59e
rlocus(sys), grid
+000i 4.93e-001 9.87e+000
-
результат - на рис. 6.11.
Рис. 6. 11.
Траектории полюсов системы SYS при изменении коэффициента передачи
6.5. Интерактивный обозреватель ltiview
Набирая в командном окне MatLAB команду ltiview, можно вызывать окно так называемого «обозревателя»
LTI-объектов, который позволяет в интерактивном режиме «строить» в этом окне практически все
вышеуказанные графики, причем для нескольких систем синхронно:
ltiview
При этом на экране появляется новое окно LTIViewer (рис. 6.12 ).
Рис. 6. 12. Окно LTI Viewer
