Лазарев Ю.Ф. Mатематическое моделирование физических процессов и технических систем в MATLAB

Подождите немного. Документ загружается.

241

Это окно состоит из нескольких частей. Главное место в нем занимает графическое поле, в котором строятся

разнообразные графики. При первом обращении к обозревателю оно пусто. В верхней части расположены

строка меню и линейка инструментов.

Меню

содержит такие команды (рис. 6.13):

File

New Viewer

открыть новый обозреватель;

Import

ввести новые LTI объекты в обозреватель;

Export

вывести объекты из обозревателя (в рабочее пространство);

ToolboxPreferences

установление (изменение) свойств графического вывода в

обозревателе;

Page Setup

установка свойств расположения графического изображения на

листе бумаги;

выведение графического изображения на принтер;

Print to Figure

выведение графического изображения в окно фигуры (это

удобно для того, чтобы воспользоваться в дальнейшем опцией

Copy Figure

для вывода графиков на печать);

закрыть обозреватель.

Рис. 6. 13. Меню File окна LTI Viewer

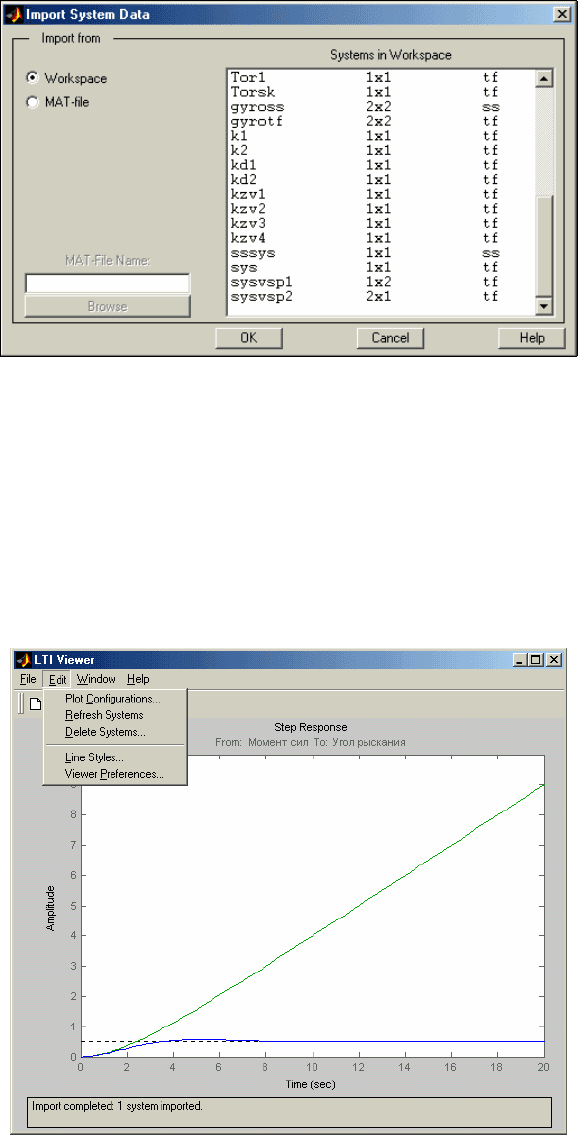
Работу с обозревателем необходимо начинать с «загрузки» в его среду тех LTI-объектов, которые нужно

анализировать. Для этого следует воспользоваться командой

Import меню File. В результате на экране

возникнет новое окно Import System Data (рис. 6.14)

242

Рис. 6. 14. Окно Import System Data

Как видим, загрузить LTI-объекты можно из рабочего пространства (переключатель WorkSpace) или из МАТ-

файла (переключатель MAT-file).

Отметим по очереди в окошке справа LTI-объекты Tor и sssys, представляющие соответственно

неуправляемое и управляемое движение торпеды по углу рыскания, и нажмем кнопку <OK>. Окно Import

System Data исчезнет, а в окне LTI Viewer появятся

две кривые, отражающие движение торпеды под

действием единичного момента сил (рис. 6.15).

Рис. 6. 15. Окно LTI Viewer с графиками систем Tor и sssys

Второе меню

Edit окна LTI Viewer содержит следующие команды (рис. 6.15):

Plot Configurations

установка вида графиков, выводимых в графическое

окно LTI Viewer, и их количества;

Refresh Systems

обновление LTI-объектов;

Delete Systems

удаление LTI-объектов;

Lyne Styles

установка стилей линий на графиках;

Viewer Preferences

установка свойств графиков.

243

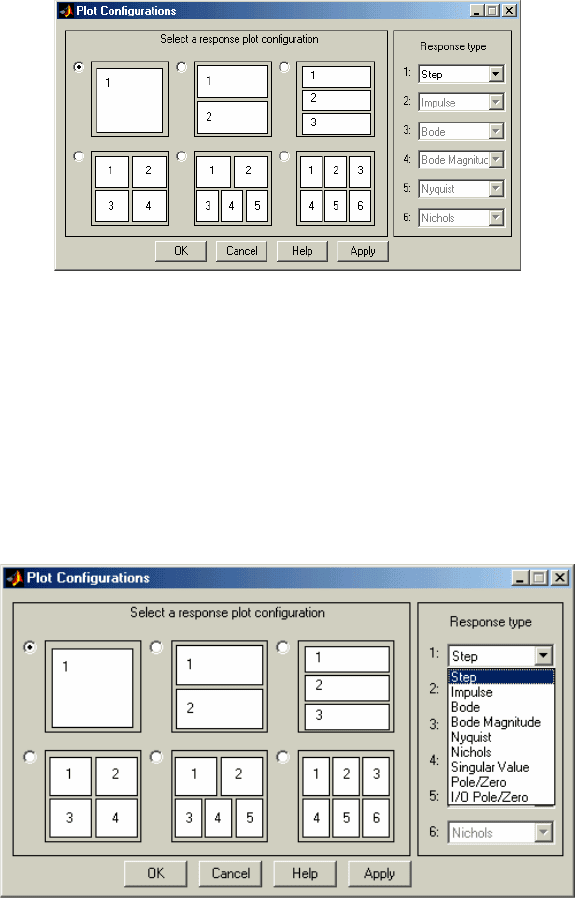
Прежде всего, следует определиться с количеством и видом графиков, выводимых в окно LTI Viewer. Их

можно установить с помощью команды

Plot Configurations меню Edit. Вызов ее приводит к появлению

на экране окна Plot Configurations (рис.6.16).

Рис. 6. 16. Окно Plot Configurations

Из рис. 6.16 видно, что предусмотрено выведение в окно LTI Viewer от одного до шести графических подокон.

По умолчанию установлен вывод одного подокна, в которое выводится график реакции системы на единичное

воздействие. Выбор количества подокон производится переключателем в верхнем левом углу

соответствующего изображения.

Тип графика, выводимого в подокно с указанным

номером, устанавливается с помощью выпадающего меню,

которым снабжено каждое окошко справа с этим номером (рис. 6.17).

Рис. 6. 17. Список графиков, выводимых в окно LTI Viewer

Возможны девять вариантов графиков (рис. 6.17):

Step – реакции системы на единичное ступенчатое воздействие;

Impulse

реакции на единичное импульсное воздействие;

Bode

АЧХ и ФЧХ системы;

Bode Magnitude

АЧХ системы;

Nyquist

диаграммы Найквиста;

Nichols

карты Николса;

Singular Value

зависимости сингулярных значений системы от частоты;

Pole/Zero

расположения нулей и полюсов системы;

I/O Pole/Zero

то же.

Выбирая соответствующую команду, устанавливают нужное изображение в указанное подокно.

244

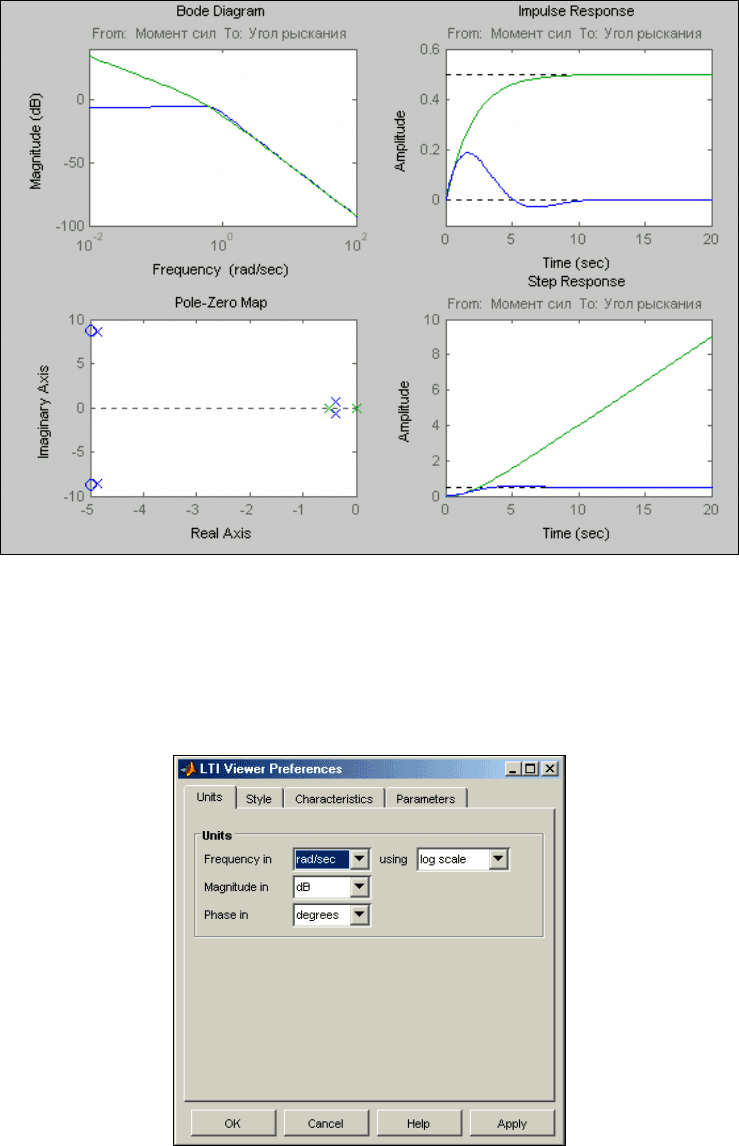
Выберем графическое окно с четырьмя подокнами. Установим в первое подокно

Bode Magnitude

, во второе –

Impulse

, в третье -

Pole/Zero

, а в четвертое –

Step

. Нажимая клавишу <OK>, получим в окне LTI Viewer

изображение, представленное на рис. 6.18.

Рис. 6. 18. Графики систем Tor и sssys, выведенные в окно LTI Viewer

Рассмотрим теперь команду

Viewer Preferences меню Edit окна LTI Viewer.

Вызывая ее, получим на экране окно LTI Viewer Preferences (рис. 6.19).

Рис. 6. 19. Окно LTI Viewer Preferences

Оно содержит четыре вкладки:

units

установки единиц измерения, в которых будут откладываться

величины по осям графиков;

style

установки кеглей текстовых символов, наносимых на графики;

245

characteristics

установки параметров некоторых численных характеристик

процессов;

parameters

установки диапазонов изменения аргументов, отличных от

принятых по умолчанию.

Как видно из рис. 6.19, по умолчанию принимаются следующие единицы измерения:

- для частоты – радианы в секунду и используется логарифмическая шкала;

- для амплитуды – дециБеллы;

- для фазы – градусы.

При помощи списков можно изменить единицы измерения частоты на Герцы, амплитуды – на абсолютные

единицы, фазы – на радианы, а шкалу по частоте сделать равномерной.

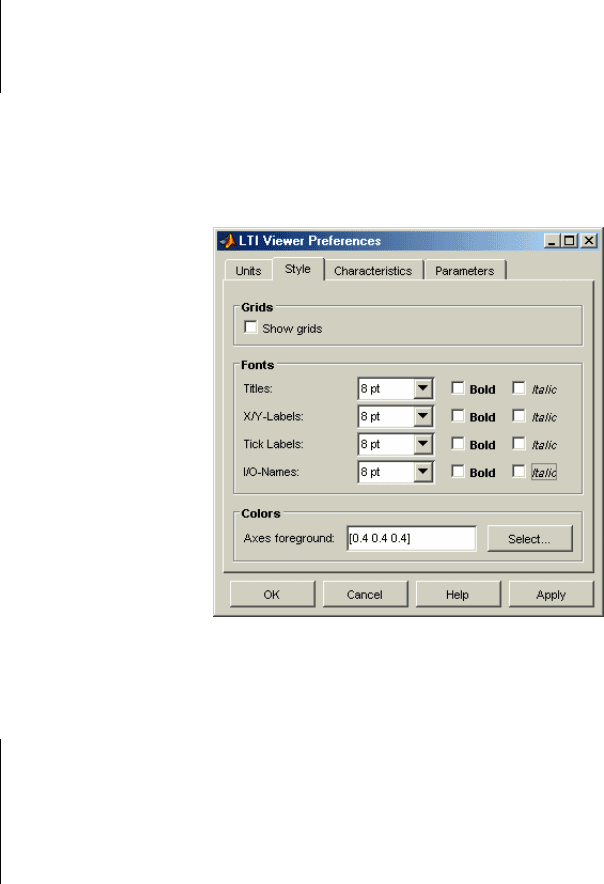
Содержание вкладки style показано на рис. 6.20.

Рис. 6. 20. Вкладка Style окна LTI Viewer Preferences

С ее помощью можно:

- установить сетку координатных линий на графиках;

- установить размер (кегль) символов, выводимых в заголовок, в надписи по осям координат, в

деления по осям, в названия входа и выхода системы;

- установить стиль символов (жирный, курсив);

- установить цвет фона.

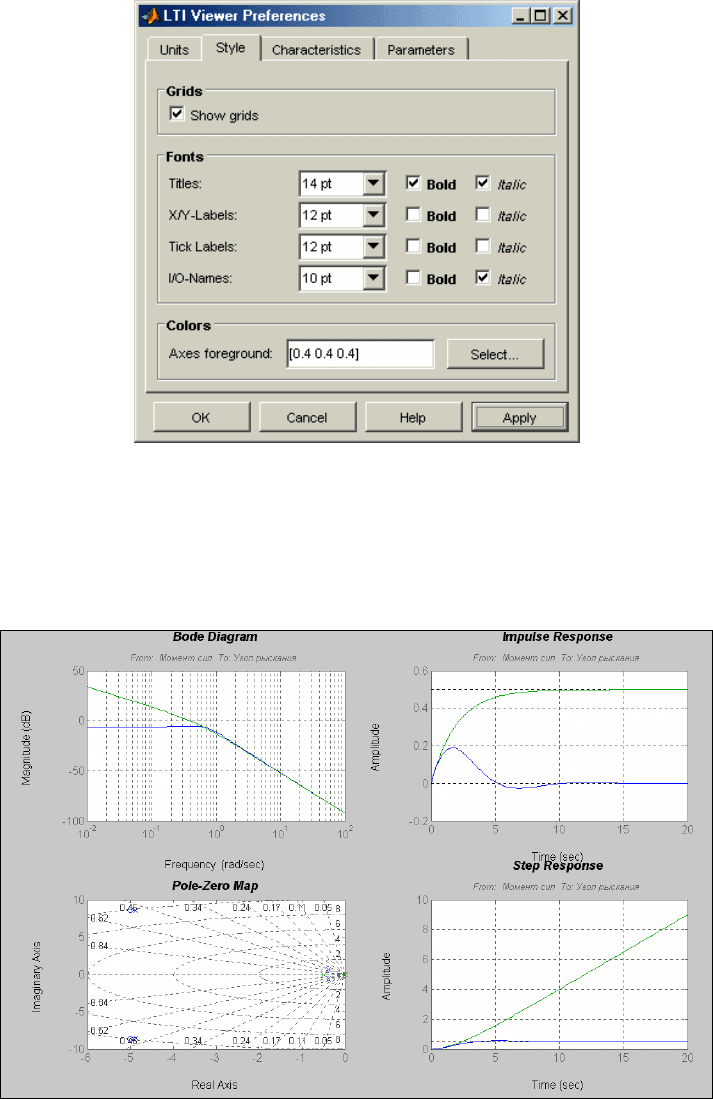
Установим разметку графиков, увеличим размеры символов в заголовках графиков до 12 кеглей, а надписей по

осям координат до 10 кеглей. Кроме того, установим жирный шрифт курсивом в заголовках (рис. 6.21).

246

Рис. 6. 21. Вкладка Style с измененными характеристиками

Закрепляя эти изменения нажатием клавиши <OK>, мы получим графическое изображение в виде,

представленном на рис. 6.22.

Рис. 6. 22. Графики систем Tor и sssys с измененными параметрами графики

Следующая вкладка -

characteristics - окна LTI Viewer Preferences показана на рис. 6.23. В ней указано,

что время установления переходного процесса определяется по уровню 2%, а время возрастания – по

промежутку времени от момента, когда значение процесса равно 10%, до момента, когда оно достигает 90%

установившегося значения. "Галочка" в окошке Unwrap phase означает, что при вычислении фазы в районе

перехода ее через

предприняты меры, чтобы она не претерпевала разрыва на .

247

Рис. 6. 23. Вкладка Characteristics окна LTI Viewer Preferences

Первые три характеристики (численные) могут быть изменены пользователем по своему усмотрению. Может

быть также снята галочка в окошке Unwrap phase. Тогда фаза может на графиках претерпевать разрывы на

радиан (что, кстати, не соответствует реальным особенностям непрерывной системы).

Вкладка parameters окна LTI Viewer Preferences представлена на рис. 6.24.

Рис. 6. 24. Вкладка Parameters окна LTI Viewer Preferences

Используя ее, можно, в случае необходимости, задать диапазоны изменения времени и частоты по

своему усмотрению.

Наконец, рассмотрим команду

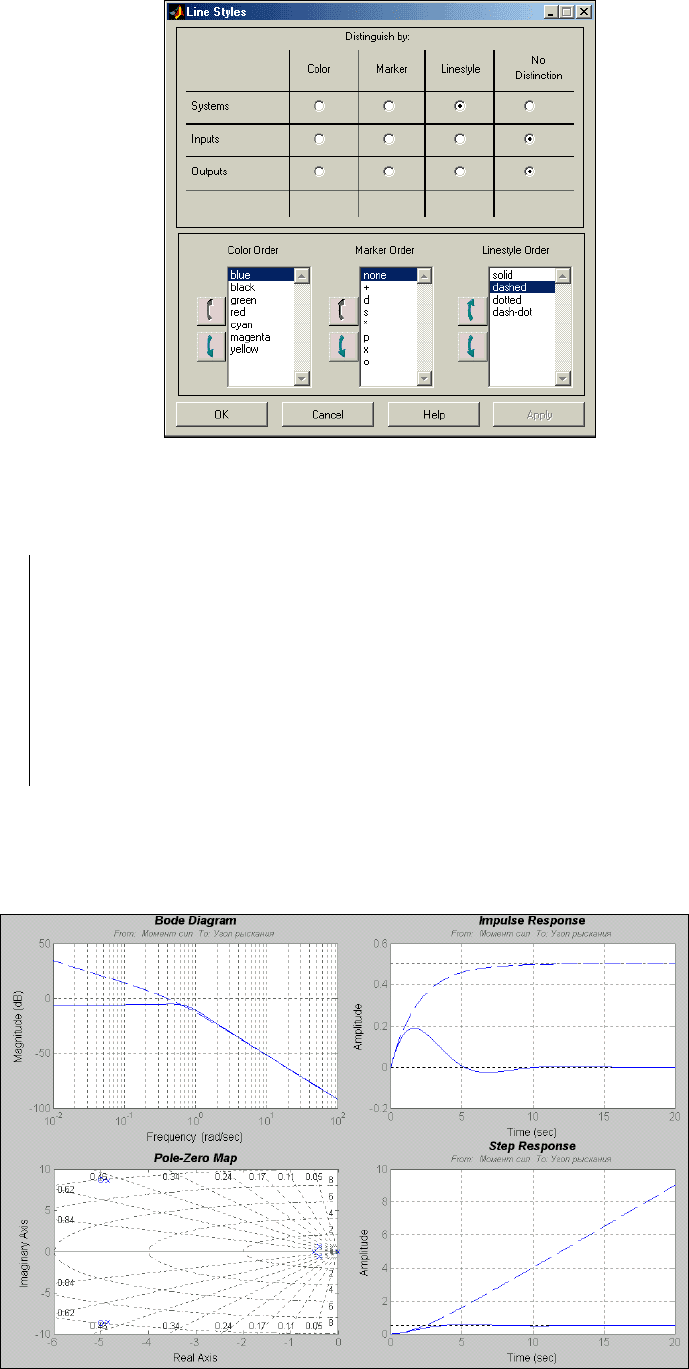
Lyne Styles меню Edit окна LTI Viewer. При ее вызове возникает

окно Line Styles, показанное на рис. 6.25.

248

Рис. 6. 25. Окно Line Styles

Установка стилей линий происходит в следующем порядке.

Сначала, с помощью верхней таблицы рис. 6.25, устанавливают какую либо одну

особенность линий, которой и будут отличаться линии на графиках, относящиеся к разным

системам (цвет, маркер или стиль линии). Для этого соответствующее свойство должно

быть отмечено переключателем под его именем в таблице.

Затем, в одном из окошек в нижней части окна, которое соответствует выбранному

свойству линии, выделяют значение этого свойства для первой LTI-системы и перемещают

его с помощью ползунков слева от окошка вверх, на верхнюю позицию. Точно так же

устанавливают на второе сверху место значение этого свойства, принимаемое для второй

системы и т. д.

Так, на рис. 6.25 установлено, что линии будут синими и различаться стилем линий. Линии первой LTI-

системы (sssys) будут сплошными, а второй (Tor) – штриховыми. Результат такой установки отражен на рис.

6.26.

Рис. 6. 26. Графики систем Tor и sssys с измененными параметрами линий

249

Для вывода содержимого графического окна LTI Viewer на печать можно использовать команду

Print to

Figure

меню

File

, которая осуществляет выведение графика предварительно в графическое окно фигуры.

Затем содержимое фигуры по обычным правилам может быть либо перенесено в окно документа текстового

редактора, либо выведено на принтер. Именно таким способом были получены рис. 6.22 и 6.26.

6.6. Синтез системы

Под синтезом САУ обычно понимают процесс разработки (проектирования, расчета параметров) одного из

звеньев САУ, обеспечивающего заданное ее качество. Пакет CONTROL содержит несколько процедур,

осуществляющих проектирование звеньев, использование которых в контуре системы управления делает САУ

оптимальной в некотором, вполне определенном смысле.

К примеру, процедура

lqr осуществляет проектирование линейно-квадратичного оптимального регулятора

для систем непрерывного времени.. При обращении к ней вида

[K,S,E] = lqr(A,B,Q,R,N) она

рассчитывает оптимальное статическое матричное звено К такое, что использование его в цепи отрицательной

обратной связи в пространстве состояния

u = - Kx (6.13)

минимизирует функционал

J =

{x'Qx + u'Ru + 2*x'Nu} dt, (6.14)

∫

если объект регулирования описывается уравнениями состояния

uBxA

⋅+⋅=

. (6.15)

Если последняя матрица N при обращении к процедуре не указана, то она принимается по умолчанию нулевой.

Одновременно вычисляется решение S алгебраических уравнений Риккати

0)()(

′

⋅⋅+⋅−⋅

′

+⋅

−

QNSBRNBSSAAS

(6.16)

и находятся собственные значения Е замкнутой системы

E = eig(A-B*K) . (6.17)

Применяя эту процедуру к ранее введенной САУ движением торпеды, получим:

[A,B,C,D]=ssdata(sssys)

Q=eye(4)

R=1

[K,S,E] = lqr(A,B,Q,R)

K =

0.4417 0.2773 0.5719 0.2926

S =

0.8834 0.5546 1.1438 0.5852

0.5546 0.4497 0.7989 0.4353

1.1438 0.7989 1.9896 1.0933

0.5852 0.4353 1.0933 1.7924

E =

-4.8886 + 8.6016i

-4.8886 - 8.6016i

-0.4718 + 0.6195i

-0.4718 - 0.6195i

Следующая процедура lqry также применяется для систем «непрерывного времени». Она отличается тем,

что, во-первых, проектируемая обратная связь по состоянию рассчитывается как дополнительная по

отношению к существующим (а не как заменяющая все уже существующие) и охватывающая только

регулируемый объект. Во-вторых, минимизируется функционал не по вектору состояния, а по выходной

величине (величинам) системы

J =

∫

{y'Qy + u'Ru + 2*y'Nu} dt. (6.18)

В этом случае входным параметром процедуры является сама ss-модель системы в форме

250

uBxA

⋅+⋅=

, . (6.19)

uDxCy

⋅+⋅=

а вызываться процедура должна таким образом

[K,S,E] = lqry(sys,Q,R,N), где sys - имя lti-модели

оптимизируемой САУ. Та же процедура может быть применена для дискретной системы (модели), уравнения

состояния которой заданы в виде конечно-разностных уравнений вида

x[n+1] = Ax[n] + Bu[n], y[n] = Cx[n] + Du[n]. (6.20)

при этом минимизируется функционал

J = Sum {y'Qy + u'Ru + 2*y'Nu}. (6.21)

Применим процедуру к рассматриваемой системе. Получаем:

Q=1; R=1;

[K,S,E] = LQRY(sssys,Q,R)

K =

0.30016 0.19769 0.24705 0.023054

S =

1.2007 0.79074 0.98822 0.092214

0.79074 0.52333 0.65394 0.064612

0.98822 0.65394 0.81717 0.080638

0.092214 0.064612 0.080638 0.012994

E =

-4.8653 + 8.5924i

-4.8653 - 8.5924i

-0.42218 + 0.62857i

-0.42218 - 0.62857i

Процедура lqrd позволяет спроектировать дискретный оптимальный линейно-квадратичный регулятор,

минимизирующий непрерывный функционал (6.14). Обращение к процедуре

[K,S,E]

=lqrd(A,B,Q,R,N,Ts)

, где Ts - заданный период дискретизации, приводит к расчету матрицы К

статического звена (6.13) обратной связи по вектору состояния системы. При этом модель системы должна

быть задана в конечно-разностной форме (6.20).

Проектирование оптимального линейного дискретного регулятора для дискретной системы с использованием

дискретного функционала (6.21) можно осуществить, используя процедуру

dlqr, например, таким образом

[K,S,E] = dlqr(A,B,Q,R,N,Ts)

. Уравнения состояния системы должны быть предварительно приведены к

конечно-разностной форме (6.20). Матрица S в этом случае представляет собой решение уравнения Риккати в

виде

A'SA - S - (A'SB+N)(R+B'SB) (B'SA+N') + Q = 0. (6.22)

Процедура

kalman осуществляет расчет (проектирование) фильтра Калмана для непрерывных или

дискретных систем автоматического управления. Обращение к процедуре имеет вид

[KEST,L,P] =

kalman(SYS,Qn,Rn,Nn)

, где SYS - имя модели системы. Для непрерывной системы

wGuBxA

⋅+⋅+⋅=

; (уравнения состояния) (6.23)

vwHuDxCy

+⋅+⋅+⋅=

, (уравнение измерения) (6.24)

с известными входами u, шумовым процессом w, шумом измерения v и шумами ковариаций

E{ww'} = Qn, E{vv'} = Rn, E{wv'} = Nn, (6.25)

фильтр KEST имеет вход [u;y] и генерирует оптимальные оценки

и соответственно величин y и x путем

решения уравнений:

)( uDxCyLuBxA

⋅−⋅−⋅+⋅+⋅=

; (6.26)

uDxCy

⋅+⋅=

. (6.27)

При этом LTI-модель SYS-системы должна содержать данные в виде (A,