Лекции - Моделирование систем
Подождите немного. Документ загружается.


Имитационное моделирование
181
Вычисляем статистики
;25
5,1
5,37
F
2
3
2
1
A
==
σ
σ
=
.3,4
5,1
5,6
F
2
3
2
2
B
==
σ
σ
=
Для уровня зна-
чимости α=0,05 и
ν
1
=1, ν
2
=2, ν
3
=2 имеем
F
1;2;0,05
=18,51 и
F
2;2;0,05
=19,0.
Сравнивая таб-
личные значения с
вычисленными стати-
стиками, имеем
A
F =25 > F
1;2;0,05
=18,51
и
B
F =4,3 > F
2;2;0,05
=19,0.
Полученные результаты позволяют сделать выводы: нулевая гипотеза
о равенстве средних по строкам не подтверждается, то есть влияние фак-
тора А на исследуемый признак значимо. Нулевая гипотеза о равенстве
средних по столбцам не опровергается, то есть влияние фактора В на ис-
следуемый признак незначимо.
Мы рассмотрели частный случай двухфакторного дисперсионного
анализа при классификации по двум признакам: в ячейке одно наблюде-
ние, взаимодействие между факторами отсутствует. В общем случае в
ячейке может и должно быть несколько наблюдений (как равное, так и не-
равное количество), между факторами может иметь место взаимодействие.
Лучше, когда в ячейке равное количество наблюдений, так как при этом
упрощаются вычисления.
Для общего случая двухфакторного анализа одно наблюдение можно
представить в виде
x
ijk
= μ + γ
i
+ δ
j
+ η
ij
+ ε
ijk
,
где μ - общее среднее,
γ
i
- эффект, обусловленный влиянием i-го уровня фактора А,
δ
j
- эффект, обусловленный влиянием j-го уровня фактора В,
η
ij
- эффект взаимодействия факторов А и В;
ε
ijk
- вариация результатов внутри отдельной ячейки.
Таблица 4.21.
Компоненты
дисперсии
Сум-
ма
квад-
ратов
Число
степе-
ней сво-
боды
Оценки
диспер-
сии
Между сред-
ними по стро-
кам (фактор А)
37,5 1 37,5
Между сред-
ними по
столбцам (фак-
тор В)
13,0 2 6,5
Остаточная 3,0 2 1,5
Полная (об-
щая)
53,5 5 10,7

Имитационное моделирование
182
Основное тождество двухфакторного дисперсионного анализа с оди-
наковым количеством наблюдений в ячейке (n) имеет вид
( )
( )
( )
( ) ( )
.QQQQ xx xxxxn
xxrn xxvn xxQ
4321
ri
1i
vj
1j
ri
1i
vj
1j
nk
1k
2
*ijijk
2
*j***i*ij
vj
1j
2
*j*
ri
1i
2
**i
ri
1i
vj
1j
nk
1k
2
ijk
+++=−++−−⋅+
+−⋅⋅+−⋅⋅=−=
∑∑ ∑∑∑
∑∑∑∑∑
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
Здесь Q
1
и Q
2
имеют тот же смысл, что и в формуле (4.43), то есть
Q
1
– сумма квадратов разностей между средними по строкам и общим
средним, характеризующая изменение признака по фактору А;
Q
2
– сумма квадратов разностей между средними по столбцам и об-
щим средним, характеризующая изменение признака по фактору В;
Q
3
– сумма квадратов, оценивающая взаимодействие факторов А и В;
Q
4
– сумма квадратов, оценивающая вариацию внутри ячейки.
Для оценки Q
1
, Q
2
, Q
3
и Q
4
находим:
- среднее значение в ячейке
∑
=
=
⋅=
nk
1
k
ijk*ij
x
n
1
x ;
- среднее значение по строке
∑
=
=
⋅=
vj
1j
*ij**i
x
v
1
x ;
- среднее значение по столбцу
∑
=
=
⋅=
ri
1
i
*ij*j*
x
r
1
x ;
- общее среднее
∑∑
=
=
=
=
⋅
⋅
=
ri
1i
vj
1j
*ij
x
vr
1
x ; (4.48)
где r - число уровней фактора А и v - число уровней фактора В.
Порядок проведения дисперсионного анализа в этом случае такой же,
как и прежде: сначала вычисляют суммы квадратов, оценки дисперсий, за-
тем отношение дисперсий
F
сравнивают с табличным.
Схема анализа и порядок вычислений сумм приведены в таблице 4.22.
Как видно из таблицы 4.22, в схеме анализа появляется новая сумма
квадратов Q
4
и несколько меняется структура суммы Q
3
(вместо x
ijk
берет-
ся
*ij
x ). Появление суммы Q
4
обусловлено наличием нескольких наблюде-
ний в ячейке. В предыдущей схеме эта сумма отсутствовала, так как при
одном наблюдении в ячейке разность (x
ijk
-
*ij
x ) равна нулю. Сумма Q
4
ха-
рактеризует влияние прочих случайных факторов (кроме факторов А, В и
их взаимодействия), поэтому для определения значимости влияния факто-
ров А и В величину дисперсии, обусловленную влиянием этих факторов,
сравнивают с дисперсией, обусловленной влиянием прочих факторов. При
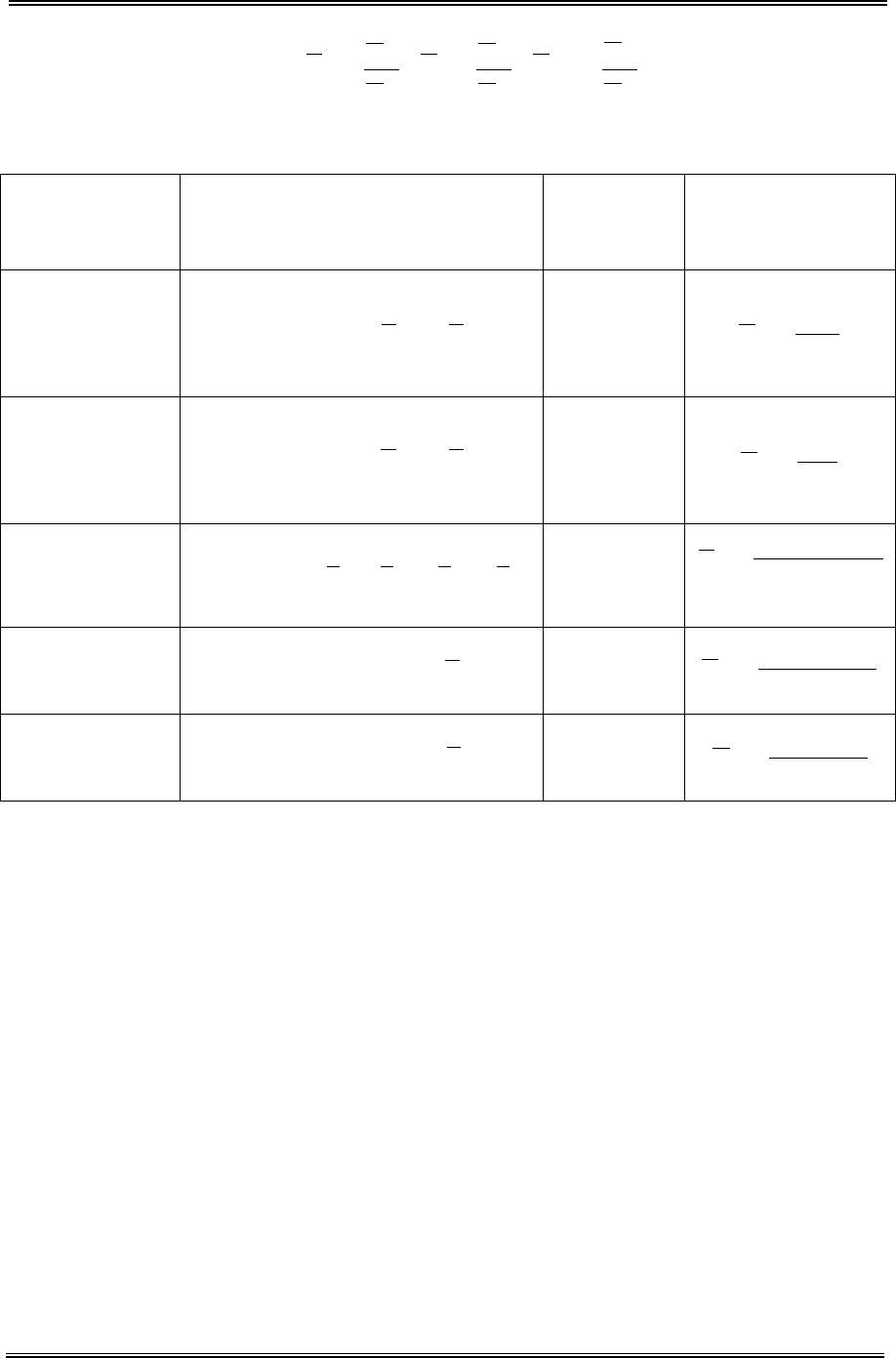
этом вычисляют следующие статистики:
Имитационное моделирование
183
.F ;F ;F
2
4
2
3
AB
2
4
2
2
B
2
4
2
1
A
σ
σ
=
σ
σ
=
σ
σ
=
Таблица 4.22.
Компоненты
дисперсии
Сумма квадратов
Число
степеней
свободы
Оценки диспер-
сии
Между сред-
ними по
строкам (по
фактору А)
( )
xxvnQ
ri
1
i
2
**i1
∑
=
=
−⋅⋅=
v-1
1
-
v
Q
1
2
1
=σ
Между сред-
ними по
столбцам (по
фактору В)
( )
xxrnQ
vj
1j
2
*j*2
∑
=
=
−⋅⋅=
r-1
1
-
r
Q
2
2
2
=σ
Взаимодей-
ствие
( )
∑∑
=
=
=
=
+−−⋅=
ri
1i
vj
1j
2
*j***i*ij3
xxxxnQ
(r-1)·(v-1)
1)-(v1)-(r
Q
3
2
3
⋅
=σ
Остаточная
( )
∑∑∑
=
=
=
=
=
=
−=
ri
1i
vj
1j
nk
1k
2
*ijijk4
xxQ
r·v·(n-1)
1)-(nvr
Q
4
2
4
⋅⋅
=σ
Полная (об-
щая)
( )
∑∑∑
=
=
=
=
=
=
−=
ri
1i
vj
1j
nk
1k
2
ijk
xxQ
r·v·n-1
1
-
n
v
r
Q
2
0
⋅⋅
=σ
Вычисленные значения сравниваются с табличными значениями
ανν ;
2
;
1
F , которые получены для заданного уровня значимости и соответст-
вующих чисел степеней свободы.
Рассмотрим пример построения двухфакторного комплекса по приве-
денной схеме.
Пример 4.28. В текстильной промышленности важным является выяв-
ление факторов, влияющих на качество пряжи, с тем, чтобы в дальнейшем
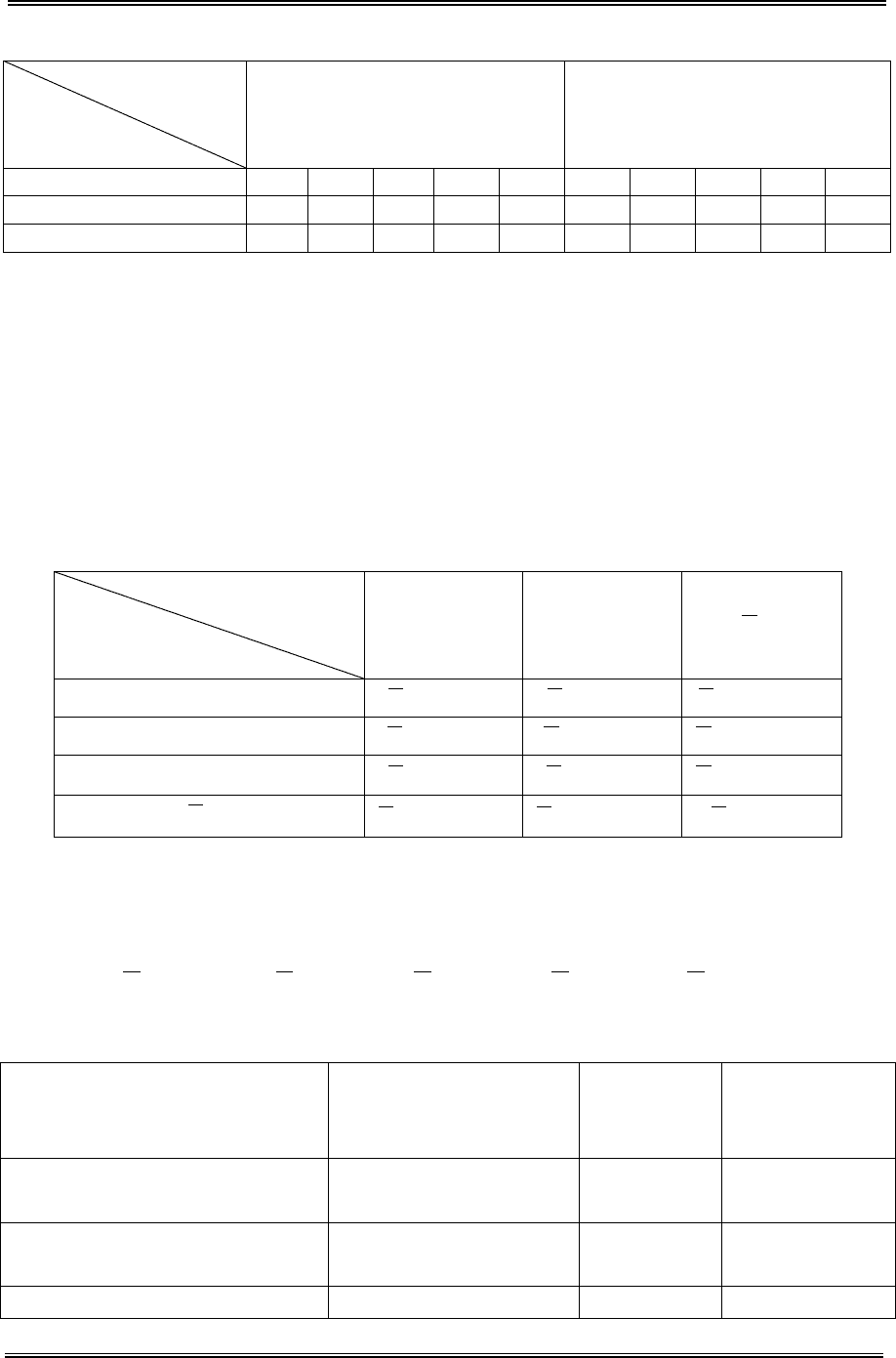
их было можно регулировать. В таблице 4.23 приведены данные о величи-
нах разрывной нагрузки в зависимости от наладки машины и партии сы-
рья.
Имитационное моделирование
184
При каждом уровне наладки машины исследованы по пять образцов
из каждой партии сырья для определения разрывной нагрузки. Требуется
выяснить, значимо ли влияют наладка машины и партии сырья на величи-
ну разрывной нагрузки.
Решение 4.28. По формулам (4.48) определяем средние значения, ко-
торые заносим в таблицу 4.24. Из нее находим Q
1
=2686,7; Q
2
=480;
Q
3
=1860; Q
4
=22360; Q=Q
1
+Q
2
+Q
3
+Q
4
=27386,7.
Отсюда оценки дисперсий:
.4,944 ;7,931 ;0,930 ;0,240 ;7,2686
2
0
2
4
2
3
2
2
2
1
=σ=σ=σ=σ=σ
Таким образом, получаем таблицу 4.25.
Таблица 4.25.
Компоненты дисперсии Сумма квадратов
Число
степеней
свободы
Оценки дис-
персии
Между средними по стро-
кам (по фактору А)
2686,7 2 2686,7
Между средними по
столбцам (по фактору В)
480,0 1 240,0
Взаимодействие 1860,0 2 930,0
Таблица 4.23.
Партии сырья
Уровень наладки
B
1
B
2
А
1
190 260 170 170 170 190 150 210 150 150
А
2
150 250 220 140 180 230 190 200 190 200
А
3
190 185 135 195 195 150 170 150 170 180
Таблица 4.24.
Партии сырья
Уровень наладки
B
1
B
2
**i
x
А
1
192x
*11
=
170x
*12
=
0,181x
**1
=
А
2
188x
*21
=
202x
*22
=
0,195x
**2
=
А
3
180x
*31
=
164x
*32
=
0,172x
**3
=
*j*
x
7,186x
*1*
=
7,178x
*2*
=
7
,
182
x
=

Имитационное моделирование
185
Остаточная 22360,0 24 931,7
Полная (общая) 27386,7 29 944,4
Вычисляем отношения дисперсий:
.26,07,931/0,240F ;88,27,931/7,2686F
BA
====
При уровне значимости α=0,05, k
4
=24 и k
1
=1 для F
A;(1;24;0,05)
=4,26 и
k
4
=24, k
3
=2 для F
В;(2;24;0,05)
=3,40. Сравнивая табличные значения с вычис-
ленными, имеем
A
F < F
A;(1;24;0,05)
и
B
F < F
B;(1;24;0,05)
. Следовательно, нулевая
гипотеза о равенстве средних на отвергается, то есть влияние фактора А
(уровня наладки машины) и фактора В (партии сырья) на величину раз-
рывной нагрузки незначимо.
4.3. Выводы по главе.
Экспеpиментальные исследования сложных технических систем в су-
щественной степени сдерживаются отсутствием именно системных мате-
матических описаний. Это не позволяет применять широко распростра-
ненное математическое моделирование. Поэтому практически единствен-
ным методом моделирования является имитация. Существенным положи-
тельным моментом здесь является то, что не обладая едиными, стандарти-
зированными технологиями построения моделей, имитационное модели-
рование является достаточно универсальным приемом, имеющим на своем
вооружении хорошо pазвитые методологии математической статистики,
программирования и других отраслей знаний.
В данной главе рассмотрены общие вопросы имитационного модели-
рования, начиная с определения имитации. Пpи этом, пpедставлены не
только сведения о достоинствах и недостатках имитационного моделиро-
вания, но и описаны известные в литературе и развитые нами методы сбо-
ра, подготовки и обработки исходной информации, освещены вопросы по-
строения моделей, проведен краткий анализ известных технологий по-
строения имитационных моделей, описаны вопросы планирования и орга-
низации эксперимента, а также обработки результатов моделирования.
Пpактическая ценность и достоверность получаемых в имитационном
моделировании результатов определяется адекватностью модели реальной
системе. В свою очередь, адекватность модели в значительной степени оп-
ределяется соответствием имитиpуемых процессов их физической сущно-
сти. Следовательно, актуальной является разработка методов воспроизве-
дения случайных событий, величин, процессов и полей с необходимыми
для исследователя вероятностными свойствами. Особое значение при этом
имеют методы генерирования случайности с заданными динамическими
(корреляционными и спектральными) свойствами. Это обусловлено необ-

Имитационное моделирование
186
ходимостью исследования функционирующих во вpемени, а не статиче-
ских систем. Известные и недостаточно распространенные методы генери-
рования случайных процессов и рассматриваются в настоящей главе.
В настоящей главе приводятся описания трех методологий построения
имитационных моделей - агрегативный подход, динамическое моделиро-
вание и индивидуальное моделирование.
Важными не только для имитационного моделирования, но и для мо-
делирования систем в целом, являются параграфы, посвященные планиро-
ванию эксперимента и обработки результатов экспериментов.
224
Моделирование сложных систем являлось и является одним из наибо-
лее мощных инструментов системных исследований. Как и любым инст-
рументарием, моделированием следует пользоваться с достаточной степе-
нью осторожности. Обратим внимание на необходимость не просто полу-
чить результаты исследований, проводимых посредством тех или иных
моделей. Крайне важно тщательно изучить исследуемую систему, с особой
тщательностью составить ее описание, подобрать методы воспроизведения
входных воздействий, построить адекватную модель, спланировать и про-
вести эксперименты, обработать и верно интерпретировать результаты.
Автор осознанно не загружал данное пособие различного рода мате-
матическими доказательствами и обоснованиями, полагая, во-первых, что
подобный материал в достаточной мере излагается в других пособиях и
литературных источниках (включая справочные) и, во-вторых, зная, что он
в достаточном объеме уже прослушан студентами в других курсах.
Традиционно курс, посвященный моделированию систем, включает
практические и лабораторные занятия, а полученные знания закрепляются
Заключение

Заключение
225
выполнением курсовой работы. Практические занятия посвящаются реше-
нию задач, разбору методик и методов и закреплению лекционного мате-
риала, отслеживая, по сути, материал, излагаемый на лекциях. Лаборатор-
ный практикум разделен на две части. Первая состоит в освоении методи-
ки статистической обработки с помощью самостоятельно выбранных сту-
дентами программных средств и на основе индивидуального, выдаваемого
каждому студенту статистического материала. Вторая часть посвящена
изучению конкретных и индивидуальных для каждого студента имитаци-
онных моделей, а именно планированию и проведению эксперимента и об-
работке получаемых результатов. Задание на курсовую работу выдается на
два-три студента. При его выполнении студенты не только разрабатывают
математические и имитационные модели, но и исследуют и самостоятель-
но разрабатывают инструментарий, обеспечивающий эффективное сис-
темное моделирование. Лучшие работы используются на следующий год в
качестве учебного материала.
Автор надеется, что настоящее пособие послужит хорошим дополне-
нием к имеющейся учебной литературе и поможет читателю более глубоко
разобраться и понять изучаемый материал.

226
1. А.с. 314208 (СССP). Генеpатоp случайных чисел / Е.И. Попов, Г.П.
Хамитов. - Опубл. в Б.И., 1971, № 27.
2. А.с. 370601 (СССP). Датчик случайных чисел / Г.П. Хамитов, Е.И.
Попов. - Опубл. в Б.И., 1973, № 11.
3. А.с. 960810 (СССP). Генеpатоp псевдослучайных процессов / А.В.
Петpов. - Опубл. в Б.И., 1982, № 35.
4. А.с. 1312569 (СССP). Генеpатоp порядковых статистик /
А.В.Петpов, С.И. Молчан, В.В.Ступин. - Опубл. в Б.И.,1987, № 19.
5. Баpский Л.А., Козин В.З. Системный анализ в обогащении полез-
ных ископаемых. - М.: Hедpа, 1978. - 486 с.
6. Баpский Л.А., Pубинштейн Ю.Б. Кибеpнетические методы в обога-
щении полезных ископаемых. - М.: Hедpа, 1970. - 312 с.
7. Бендат Дж., Пиpсол А. Измеpение и анализ случайных процессов. -
М.: Наука, 1974. - 399 с.
8. Бокс Дж., Дженкинс P. Анализ временных рядов. Пpогноз и управ-
ление. - М.: Миp, 1974. - 557 с.
Литература

Литература
227
9. Бусленко В.H. Автоматизация имитационного моделирования
сложных систем. - М.:Hаука,1977. - 240 с.
10. Бусленко H.П., Калашников В.В., Коваленко И.H. Лекции по тео-
рии сложных систем. - М.: Советское радио, 1973. - 439 с.
11. Бусленко H.П. Моделиpование сложных систем. - М.: Наука, 1978.
- 339 с.
12. Быков В.В. Цифpовое моделирование в статистической радиотех-
нике. - М.: Советское радио, 1971. - 328 с.
13. Веников В.А. Теоpия подобия и моделирование. - М.: Высшая
школа, 1976. - 479 с.
14. Вентцель Е.С. Теоpия вероятностей. - М.: Наука, 1969. - 576 с.
15. Гихман И.И., Скоpоход А.В. Введение в теорию случайных про-
цессов. - М.: Наука, 1977. - 568 с.
16. Гладышев Е.Г. О периодически коррелированных случайных про-
цессах. // Доклады АН СССP, т.137, № 5, 1961. - с.1026-1029.
17. Гнеденко Б.В. Куpс теории вероятностей. - М.: Наука, 1988. - 448
с.
18. Голенко Д.И. Моделиpование и статистический анализ псевдослу-
чайных чисел на ЭВМ. - М.: Наука, 1965. - 227 с.
19. Ермаков С.М., Метод Монте-Каpло и смежные вопросы. - М.:
Наука, 1975. - 471 с.
20. Закс Л. Статистическое оценивание. - М.: Статистика, 1976. - 598
с.
21. Иоффе В.М., Леоненко С.С., Петpов А.В. Частотноpегулиpуемый
электропривод гоpнообогатительных предприятий. - Иркутск: Изд-во
Иpкутского госуд. унив., 1988. - 152 с.
