Лекции по гидравлике

Подождите немного. Документ загружается.

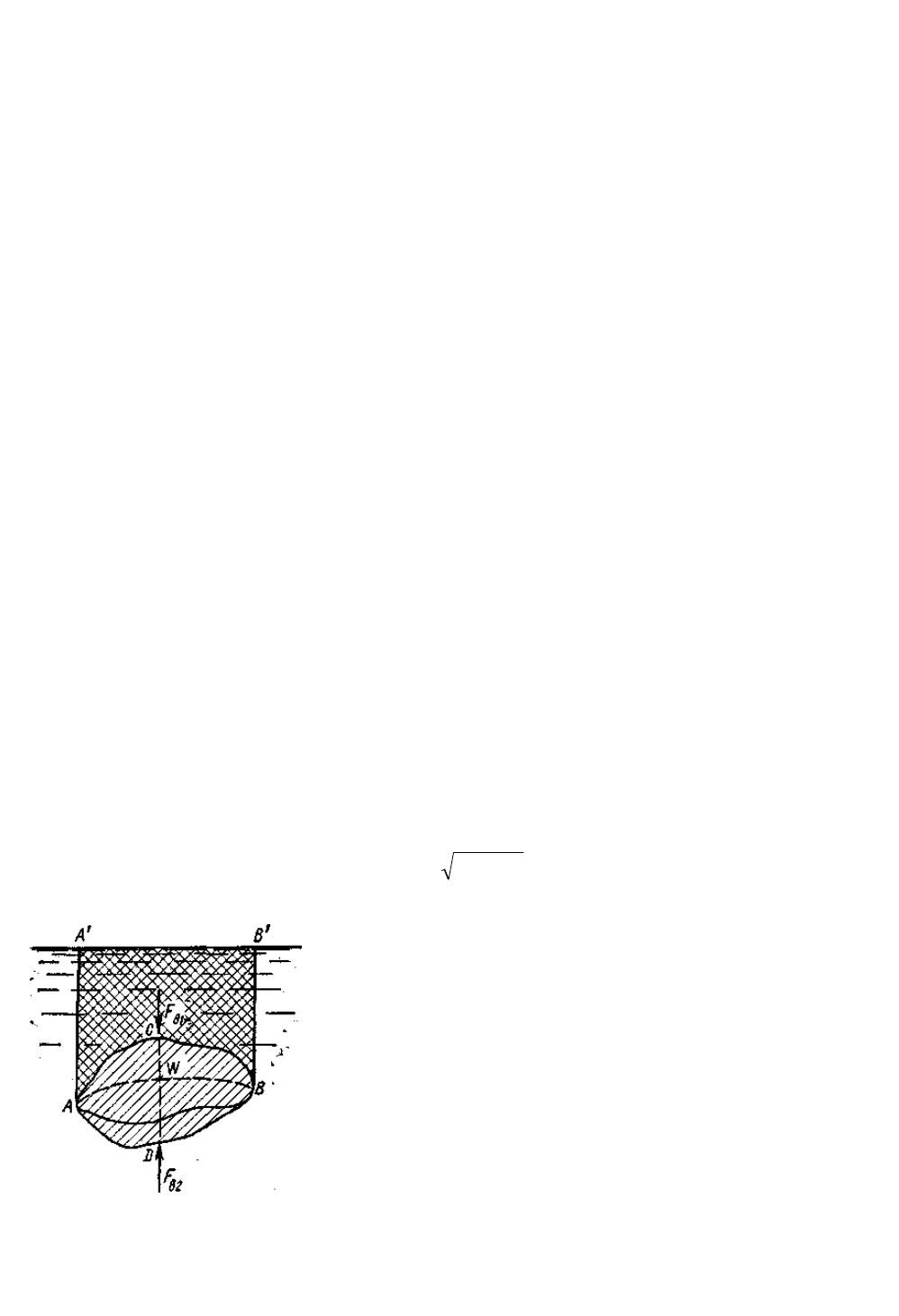
Рис1.9,а Рис1.9,б

(Рис. 1.9) Схема для определения силы давления жидкости на цилиндрическую

поверхность

1) жидкость расположена сверху (рис. 1.9, а);

2) жидкость расположена снизу (рис. 1.9, б).

В первом случае выделим объем жидкости, ограниченный рассматриваемой

поверхностью АВ, вертикальными поверхностями, проведенными через границы

этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и

рассмотрим условия его равновесия в вертикальном и горизонтальном

направлениях. Если жидкость действует на стенку АВ с силой

, то стенка АВ

действует на жидкость с силой

, направленной в обратную сторону. На рис. 1.15

показана эта сила реакции, разложенная на две составляющие: горизонтальную

и вертикальную

Условие равновесия объема ABCD в вертикальном направлении имеет вид

= p

+ G, (1.31)

где

— давление на свободной поверхности жидкости; S

— площадь

горизонтальной проекции поверхности АВ; G — вес выделенного объема

жидкости.

Условие равновесия того же объема в горизонтальном направлении запишем с

учетом того, что силы давления жидкости на поверхности ЕС и AD взаимно

уравновешиваются и остается лишь сила давления на площадь BE, т. е. на

вертикальную проекцию поверхности АВ — S

. Тогда

ρgh

(1.32)

Определив по формулам (1.31) и (1.32) вертикальную и горизонтальную

составляющие полной силы давления

F, найдем

ГB

FFF 

Рис 1.10. Схема для подтверждения закона Архимеда.

Когда жидкость расположена снизу (см. рис. 1.9, б), гидростатическое давление

во всех точках поверхности АВ имеет те же значения, что и в первом случае, но

направление его будет противоположным, и суммарные силы F

и F

определятся

теми же формулами (1.31) и (1.32), но с обратным знаком. При этом под

величиной G следует понимать так же, как и в первом случае, вес жидкости в

объеме ABCD, хотя этот объем и не заполнен жидкостью.

Положение центра давления на цилиндрической стенке можно легко найти,

если известны силы F

ж F

n определены центр давления на вертикальной

проекции стенки и центр тяжести выделенного объема ABCD. Задача значительно

облегчается в том случае, когда рассматриваемая цилиндрическая поверхность

является круговой. Равнодействующая сила при этом пересекает ось поверхности,

так как любая элементарная сила давления нормальна к поверхности, т. е.

направлена по радиусу.

Изложенный способ определения силы давления на цилиндрические

поверхности применим и к сферическим поверхностям, причем

равнодействующая сила в этом случае также проходит через центр поверхности и

лежит в вертикальной плоскости симметрии.

Описанный выше прием нахождения, вертикальной составляющей силы

давления жидкости на криволинейную стенку используют для доказательства

закона Архимеда.

Пусть в жидкость погружено тело произвольной формы объемом V (рис. 1.16).

Спроектируем его на свободную поверхность жидкости и проведем

проектирующую цилиндрическую поверхность, которая касается поверхности

тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела

АСВ от нижней ее части ADB. Вертикальная составляющая F

силы избыточного

давления жидкости на верхнюю часть поверхности тела направлена вниз и равна

весу жидкости в объеме АА'В'ВСА. Вертикальная составляющая F

силы давления

жидкости на нижнюю часть поверхности тела направлена вверх и равна весу

жидкости в объеме AA'B'BDA. Отсюда следует, что вертикальная

равнодействующая сил давления жидкости на тело будет направлена вверх и

равна весу жидкости в объеме, равном разности указанных двух объемов, т. е.

-F

ACBD

ρg

В этом и заключается закон Архимеда, обычно формулируемый так: на тело,

погруженное в жидкость, действует выталкивающая сила, направленная

вертикально вверх, численно равная весу жидкости, вытесненной телом, и

приложенная в центре тяжести объема погруженной части тела.

Сила FA называется архимедовой силой, или силой поддержания, а точка ее

приложения, т. е. центр тяжести объема F, — центром водоизмещения.

В зависимости от соотношения веса G тела и архимедовой силы FA возможны

три случая: 1) G > F

— тело тонет;

2) G < F

— тело всплывает и плавает на поверхности жидкости в

частично погруженном состоянии; 3) G = F

— тело плавает в полностью

погруженном состоянии.

Для равновесия плавающего тела кроме равенства сил G = F

должен быть

равен нулю суммарный момент. Последнее условие соблюдается тогда, когда

центр тяжести тела лежит на одной вертикали с центром водоизмещения. Условие

устойчивого равновесия тела, плавающего в полностью погруженном состоянии,

заключается в следующем: центр тяжести тела должен находиться ниже центра

водоизмещения. Устойчивость равновесия тел, плавающих на поверхности

жидкости, здесь не рассматривается.

1.3 Кинематика

Понятие о движении жидкости как непрерывной деформации сплошной

материальной среды

Кинематика жидкости является разделом гидромеханики, в котором движение

изучается вне зависимости от действующих сил; в кинематике устанавливаются

связи между геометрическими характеристиками движения и временем.

Кинематика жидкости существенно отличается от кинематики твердого тела.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой,

то в движущейся жидкой среде такие связи отсутствуют; эта среда состоит из

множества частиц, движущихся одна относительно другой.

Скорость в данной точке пространства, занятого движущейся жидкостью,

является функцией координат этой точки, а иногда и времени. Таким образом,

задачей кинематики жидкости является определение скорости в любой точке

жидкой среды, т. е. нахождение поля скоростей.

В опытах наблюдать движение жидких частиц и измерять их скорости

можно различными способами. Простейшим является подкрашивание частиц

краской мой же плотности, что и изучаемая жидкость. Наблюдения за

поведением таких подкрашенных частиц показывают, что при определённых

условиях частицы могут двигаться упорядоченно, образуя слоистое или

ламинарное течение. При других условиях частицы, наряду с основным

движением по некоторому преимущественному направлению, перемещаются

из слоя в слой, их мгновенные скорости резко изменяются по величине и

направлению. Иными словами, в этом случае на упорядоченное движение

частиц накладывается хаотическое или пульсационное движение, приводящее

к разрушению слоистой структуры и перемешиванию слоёв. Такое движение

получило название турбулентного.

Сначала рассмотрим движение так называемой идеальной жидкости, т. е. такой

воображаемой жидкости, которая совершенно лишена вязкости, а затем

перейдем к изучению реальных потоков. В такой невязкой жидкости, так же

как и в неподвижных реальных жидкостях, возможен лишь один вид напряжений

— нормальные напряжения сжатия, т. е. гидромеханическое давление, или просто

давление.

Давление в движущейся идеальной жидкости обладает теми же свойствами,

что и в неподвижной жидкости, т. е. на внешней поверхности жидкости оно

направлено по внутренней нормали, а в любой точке внутри жидкости — по

всем направлениям одинаково.

Ламинарные течения жидкости могут быть установившимися

(стационарными) или неустановившимися (нестационарными). Турбулентные

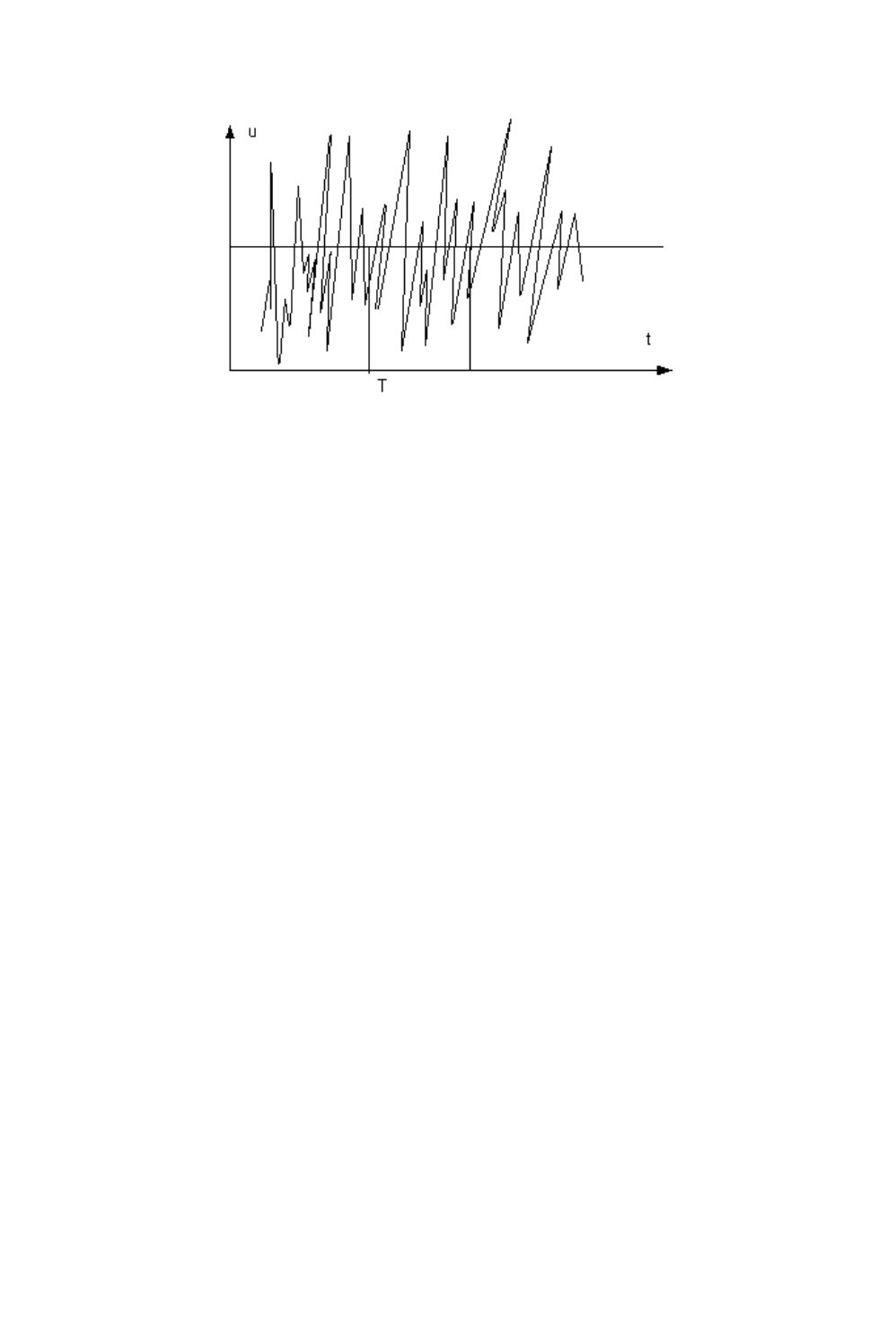
течения всегда являются неустановившимися; хаотическое движение частиц в

турбулентном потоке создаёт резкие изменения местных скоростей во времени,

называемые пульсациями скорости.

Рис 1.11 Результаты измерений местной мгновенной скорости

турбулентного потока воздуха.

На (рис.1.11) приведены результаты измерений местной мгновенной скорости

турбулентного потока воздуха. Местная скорость меняется во времени

достаточно резко, однако её величина колеблется около некоторого среднего во

времени значения. Поскольку пользование в расчётах мгновенными значениями

скоростей приводит к трудностям и некоторой неопределённости, то вводится

понятие местной усреднённой скорости, которая определяется соотношением

U=1/T Sudt,

Где U-мгновенная местная скорость; T-период усреднения.

Установившееся и неустановившееся течение жидкости

Установившимся называется течение жидкости, неизменное по времени, при

котором давление и скорость являются функциями только координат, но не

зависят от времени. Давление и скорость могут изменяться при перемещении

частицы жидкости из одного положения в другое, но в данной неподвижной

относительно русла точке давление и скорость при установившемся

движении не изменяются по времени, т. е.

P=f

(x,y,z), v=f

(x,y,z).

В частном случае установившееся течение может быть равномерным, когда

скорость каждой частицы не изменяется с изменением ее координат, и поле

скоростей остается неизменным вдоль потока.

Неустановившимся называется течение жидкости, все характеристики

которого (или некоторые из них) изменяются по времени в точках

рассматриваемого пространства.

В общем случае неустановившегося течения давление и скорость зависят как

от координат, так и от времени:

P=F

(x,y,z,t), v=F

(x,y,z,t).

Примерами неустановившегося течения жидкости могут служить быстрое

опорожнение сосуда через отверстие в дне или движение во всасывающей

или напорной трубе поршневого насоса, поршень которого совершает

возвратно-поступательное движение. Примером установившегося течения

может служить истечение жидкости из сосуда, в котором поддерживается

постоянный уровень, или движение жидкости в трубопроводе, создаваемое

центробежным насосом с постоянной частотой вращения вала.

Исследование установившихся течений гораздо проще, чем не-

установившихся. Траектории частиц жидкости при установившемся течении

являются неизменными по времени.

При неустановившемся течении траектории различных частиц,

проходящих через данную точку пространства, могут иметь разную форму.

Наглядное представление о поле скоростей движущейся жидкости можно

получить, если построить векторные линии этого поля, называемые в

гидромеханике линиями тока.

Линией тока называется кривая, в каждой точке которой вектор скорости

в данный момент времени направлен по касательной .

Очевидно, что в условиях установившегося течения линия тока совпадает

с траекторией частицы и не изменяет своей формы с течением времени.

Линии токов жидкости и вихревые линии. Плавно и резко

изменяющееся движение

Если в движущейся жидкости взять бесконечно малый замкнутый

контур и через все его точки провести линии тока, то образуется трубчатая

поверхность, называемая трубкой тока. Часть потока, заключенная внутри

трубки тока, называется элементарной струйкой. При стремлении

поперечных размеров струйки к нулю она в пределе стягивается в

линию тока.

В любой точке трубки тока, т. е. боковой поверхности струйки, векторы

скорости направлены по касательной, а нормальные к этой поверхности

составляющие скорости отсутствуют, следовательно, при установившемся

движении ни одна частица жидкости, ни в одной точке трубки тока не может

проникнуть внутрь струйки или выйти наружу. Трубка тока, таким образом,

является как бы непроницаемой стенкой, а элементарная струйка представляет

собой самостоятельный элементарный поток.

Рис 1.12 Рис 1.3

Линии тока Трубка тока

Потоки конечных размеров будем сначала рассматривать как совокупность

элементарных струек, т. е. будем предполагать течение струйным. Из-за

различия скоростей соседние струйки будут скользить одна по другой, но не

будут перемешиваться одна с другой. Живым сечением, или просто сечением

потока, называется в общем случае поверхность в пределах потока,

проведенная нормально к линиям тока. Далее будем рассматривать в

потоках такие участки, в которых струйки можно считать параллельными и,

следовательно, живые сечения — плоскими.

Различают напорные и безнапорные течения жидкости. Напорными

называют течения в закрытых руслах без свободной поверхности, а

безнапорными — течения со свободной поверхностью. При напорных течениях

давление вдоль потока обычно переменное, при безнапорном — постоянное (на

свободной поверхности) и чаще всего атмосферное. Примерами напорного

течения могут служить течения в трубопроводах с повышенным (или

пониженным) давлением, в гидромашинах или других гидроагрегатах.

Безнапорными являются течения в реках, открытых каналах и лотках.

Расходом называется количество жидкости, протекающее через живое течение

потока (струйки) в единицу времени. Это количество можно измерить в единицах

объёма, в весовых единицах или в единицах массы, в связи с чем различают

объёмный Q, весовой Q

и массовый Q

расходы.

Для элементарной струйки, имеющий бесконечно малые площади сечений,

можно считать истинную скорость одинаковой во всех точках каждого сечения.

Следовательно, для этой струйки объёмный(м

/с), весовой(Н/с) и массовый(кг/с)

расходы

dSvdQ 

;

dQ;gpdQ



dSvpdQpdQ



Для потока конечных размеров в общем случае скорость имеет различное

значение в разных точках сечения, поэтому расход надо определять как сумму

элементарных расходов струек.

Обычно в рассмотрение вводят среднюю по сечению скорость

ср

=Q/S, откуда Q= v

ср

Основываясь на законе сохранения вещества, на предположении о

сплошности (неразрывности) течения и на указанном выше свойстве трубки тока,

заключающемся в ее «непроницаемости», для установившегося течения

несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях

элементарной струйки один и тот же:

dQ=v

=const (вдоль струйки)

Это уравнение называется уравнением объемного расхода для элементарной

струйки.

Аналогичное уравнение можно составить и для потока конечных размеров,

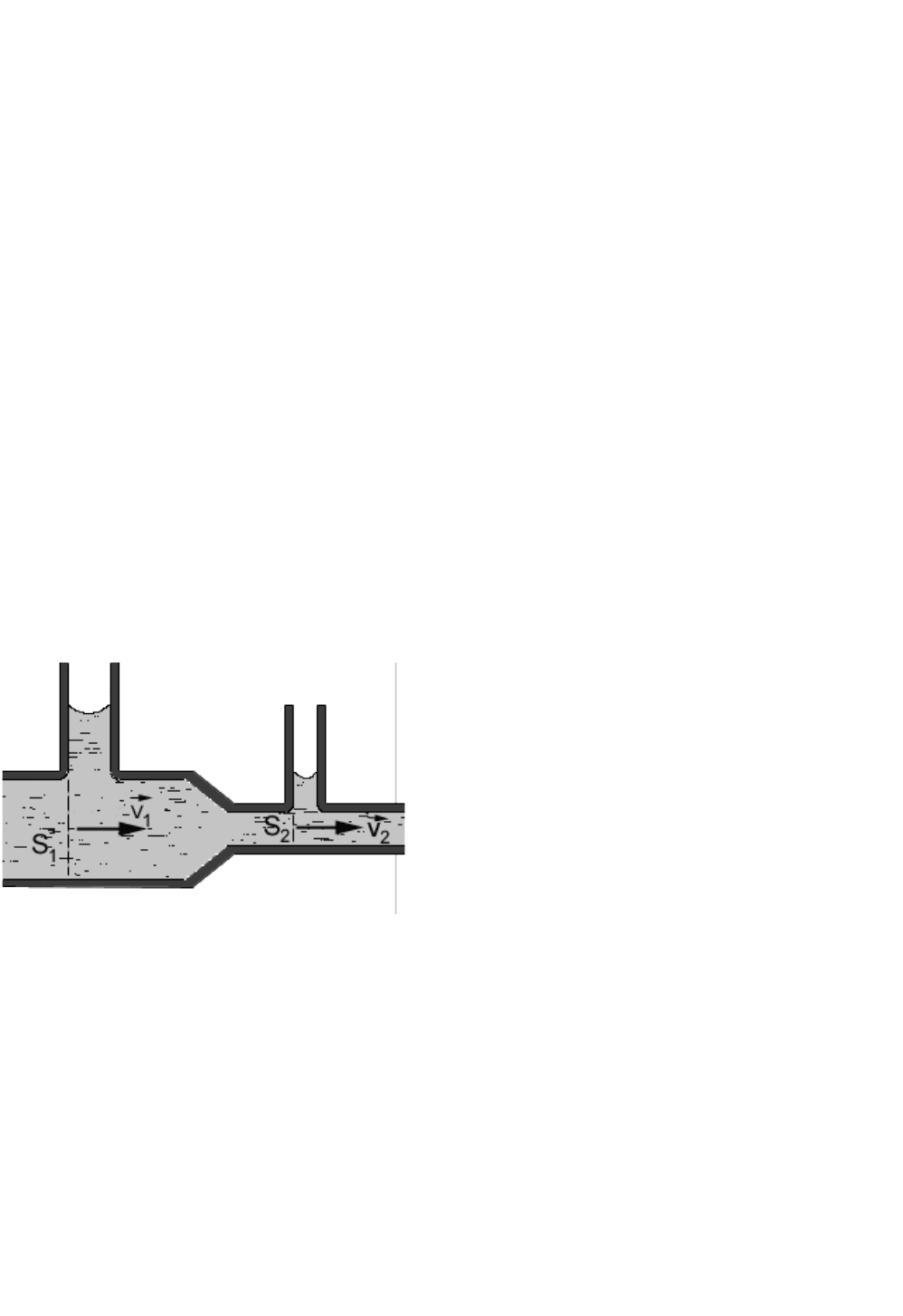
ограниченного непроницаемыми стенками, только вместо истинных скоростей

следует ввести средние скорости.

1.4 Общие уравнения сплошной среды

Уравнение неразрывности

Рассмотрим случай, когда невязкая жидкость течет по горизонтальной

цилиндрической трубе с изменяющимся поперечным сечением .

Течение жидкости называют стационарным, если в каждой точке

пространства, занимаемого жидкостью, ее скорость с течением времени не

изменяется. При стационарном течении через любое поперечное сечение трубы за

равные промежутки времени переносятся одинаковые объемы жидкости.

Жидкости практически несжимаемы, т. е. можно считать, что данная масса

жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов

жидкости, проходящих через разные сечения трубы, означает, что скорость

течения жидкости зависит от сечения трубы.

Пусть скорости стационарного течения жидкости через сечения трубы S

равны соответственно v

и v

. Объем жидкости, протекающей за промежуток

времени t через сечение S

, равен V

t, а объем жидкости, протекающей за то

же время через сечение S2, равен V

t. Из равенства V

следует, что

1221

VSVS 

(1.27)

Соотношение (1.27) называют уравнением неразрывности. Из него следует, что

2121

// SSVV 

Следовательно, при стационарном течении жидкости скорости

Рис 1.14

движения ее частиц через разные поперечные сечения трубы обратно

пропорциональны площадям этих сечений.

Поскольку объемный расход Q равен произведению скорости текущей

среды V на площадь S поперечного сечения трубки тока, уравнение

неразрывности имеет следующий вид:

2211

VSVSQ 

(1.28)

Это уравнение выражает один из основных законов гидроаэромеханики, согласно

которому объемный расход во всякой трубке тока, ограниченной соседними

линиями тока, должен быть в любой момент времени одинаков во всех ее

поперечных сечениях.

Уравнение Бернулли

Основной задачей гидродинамики является изучение законов движения жидкости.

Движение жидкости характеризуется скоростями движения частиц и давлением в

отдельных точках потока.

Чтобы установить взаимосвязь между основными параметрами движения, а

именно между гидродинамическим давлением и скоростью движущейся

жидкости, составим уравнения движения жидкости. Эти уравнения могут быть

получены из дифференциальных уравнений равновесия жидкости, если к

действующим силам согласно принципу д’Аламбера присоединить силы инерции.

Получим систему уравнений:

















(1.29)









Преобразуем полученные уравнения, применительно к элементарной струйке

идеальной жидкости, находящейся в установившемся движении, умножив каждое

уравнение соответственно на

,dx

. После по членного суммирования

получаем



























 dz

dzZdyYdxX





(1.30)

Так как

- это проекции элементарного пути, проходимого частицами

жидкости за время dt, следовательно:



(1.31)

С учетом (3) уравнение (2) примет вид:



























 dz

dzZdyYdxX



zzyyxx

duuduuduu 

(1.32)

dФZdzYdyXdx 

- полный дифференциал силовой функции, выражающей

массовые силы, под действием которых осуществляется движение жидкости.

dPdz



























- полный дифференциал давления, так как при

установившемся движении гидродинамическое давление не зависит от времени.

 

)(

2222

uduuudduuduuduu

zyxzzyyxx



- полный дифференциал скорости,

выраженной через ее составляющие по соответствующим осям координат.

С учетом вышесказанного уравнение (1.32) примет вид:

)(

uddPdФ 



(1.33)

Или окончательно

0)(

 dФuddP



(1.34)

В частном случае, когда из всех массовых сил на движущуюся жидкость

действуют только силы тяжести, силовая функция будет равна

dzgdФ 

(1.35)

Подставив значение силовой функции в уравнение (6) и проинтегрировав,

получим уравнение для рассматриваемого сечения:

constzg





(1.36)

Так как сумма трех членов в уравнении (8) постоянна для любого сечения

струйки, то для двух сечений 1 - 1 и 2 - 2 (рис. 1.15) можно записать





(1.37)

Рис. 1.15

Разделив левую и правую часть уравнения (1.37) на g, окончательно получим:





(1.38)

Уравнение (10) устанавливает связь между скоростью движения, давлением и

геометрическим положением частиц жидкости для двух сечений струйки и

является уравнением Бернулли для элементарной струйки идеальной жидкости.

Геометрическая и энергетическая интерпретация уравнения Бернулли

Для определения геометрического смысла уравнения Бернулли

рассмотрим элементарную струйку движущейся жидкости относительно

произвольно выбранной плоскости сравнения (рис. 1.16). Выберем три сечения: 1 -

1; 2 - 2; 3 - 3; центры тяжести которых относительно плоскости сравнения 0 - 0

расположены на высотах z

; z

В центры тяжести выбранных сечений установим пьезометры и трубки Пито.

Трубка Пито - это изогнутая под углом 90

трубка, устанавливаемая отверстием

наконечника против течения. Под действием давления жидкость в пьезометрах

поднимается на высоту

)/( gPh





В трубках Пито, под действием давления и скорости жидкость поднимается выше

уровня в пьезометрах на высоту

)2/(

guh



(рис. 1.16).