Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection
Подождите немного. Документ загружается.


January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
320 Principles of Radiation Interaction in Matter and Detection
For describing such a process in the framework of statistical physics [Chan-
drasekhar (1943); Parker (1965)], one needs to introduce the phase-space
†
distri-
bution function (also termed distribution function) F (~x, ~v, t) for the particle distri-
bution at the time t over position ~x and velocity ~v, so that the d
6
N
p
number of
particles in a d
3
x volume element around the configuration space location ~x with
velocity vectors between ~v and ~v + d
3
v is given by:
d
6
N
p
= F (~x, ~v, t) d
3
x d
3
v,
with the corresponding normalized phase-space distribution f (~r, ~v, t) defined as
f(~x, ~v, t) =
F (~x, ~v, t)
RR R
F (~x, ~v, t) d
3
v
=
F (~x, ~v, t)
n(~x, t)
,
where the (particle) number density (or particle concentration) is
n(~x, t) =
ZZZ
F (~x, ~v, t) d
3
v.
The average (or bulk) velocity ~v
bl
(~x, t) is obtained from
~v
bl
(~x, t) =
RR R
~v F (~x, ~v, t) d
3
v
n(~x, t)
.
The evolution of the (normalized) phase-space distribution function is described
by the Boltzmann equation (e.g., see Section 2.1.2 of [Cravens (1997)], Section 2.2
of [Gombosi (1998)], Section 5.2.1 of [Kallenrode (2004)]), in which the total time
derivative of such a distribution is equal to the rate of change of the phase-space di-
stribution or collision term. For a Markhoff process, Chandrasekhar (1943) demon-
strated that the collision term can be treated using the so-called Fokker–Plank ap-
proximation (or diffusion approximation) and, consequently, obtaining the so-called
Fokker–Plank equation.
As already mentioned, within the Parker model (see Sect. 4.1.2.1) magnetic
irregularities are carried outwards by the SW with speed ~v
w
. These irregularities
are treated as the elastic scattering centers of GCRs in the reference frame moving
with the SW. In the Parker–Gleeson–Axford–Jokipii treatment the collision term
of the Markhoff process, resulting in the modulation phenomenon of CRs, is firstly
evaluated in the SW frame moving with scatterers, then is transformed to a fixed
heliocentric frame [Parker (1965); Gleeson and Axford (1967, 1968a,b); Jokipii and
Parker (1970); Jokipii (1971)]). In the heliocentric system, in which the spatial
coordinates x
i
allow one to determine the position ~r at a heliocentric distance r,
the derived Fokker–Plank equation
∗∗
is given by
∂U
∂t
−
∂
∂x
i
µ
K
i,j
∂U
∂x
J
¶
+
∂
∂T
0
µ
U
dT
0
dt
¶
+
∂
∂x
i
(U v
w,i
) = 0, (4.35)
†
In classical non-relativistic statistical mechanics, a particle is represented by a single point in
a six-dimensional phase space, i.e., the three spatial (for location ~x in the so-called configuration
space) and three velocity coordinates (for the location ~v in the so-called velocity space). ~x and ~v
are the Eulerian coordinates of the phase space.
∗∗
In this section, when an index variable appears twice in a single term, it implies that we are
summing over all of its possible values; for instance, the divergence of the SW velocity is expressed
by ∂v
w,i
/∂x
i
(e.g., see [Parker (1965)]). This notation is sometime referred to as the Einstein
summation convention.
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Radiation Environments and Damage in Silicon Semiconductors 321
where T
0
is the kinetic energy of the cosmic-ray particle in the moving frame,
U(x
i
, T
0
, t) is the number density
‡
of CR particles having kinetic energy T
0
at the
position ~r and time t and, finally, K
i,j
is the so-called diffusion tensor [Parker (1965);
Jokipii and Parker (1970); Jokipii (1971)]. The third term of Eq. (4.35) is derived
under the assumption that a possible Fermi acceleration
¶
of CR particles can be
neglected [Parker (1965); Jokipii and Parker (1970)]). For a cosmic-ray particle, the
largest difference
‡‡
|∆T | of its kinetic-energy between the moving and heliocentric
frames can be computed from [see Eqs. (1.20, 1.23)]
T + m
r
c
2
= γ
w
·
¡
T
0
+ m
r
c
2
¢
± β
w
q
(T
0
+ m
r
c
2
)
2
− m
2
r
c
4
¸
= γ
w
h
¡
T
0
+ m
r
c
2
¢
± β
w
p
T
0
(T
0
+ 2m
r
c
2
)
i
, (4.36)
where T is the kinetic energy in the heliocentric frame, m
r
is the rest mass of the
cosmic-ray particle and
β
w
=
v
w
c
.
For a typical SW speed of ≈ 470 km/s (see page 300), we have β
w
≈ 1.57 × 10
−3
and γ
w
≈ 1 [Eq. (1.4)]. Thus, from Eq. (4.36), we obtain
|∆T | ≈ β
w
p
T
0
(T
0
+ 2m
r
c
2
)
≈ 1.57 × 10
−3
p
T
0
(T
0
+ 2m
r
c
2
), (4.37)
⇒
|∆T |
T
0
≈ 1.57 × 10
−3
r
1 +
2m
r
c
2
T
0
. (4.38)
From ≈ 100 MeV up to ≈ 10 GeV per nucleon
∗
, by means of Eq. (4.38) |∆T |/T
0
is
estimated ≈ (0.70–0.17) %. Thus, |∆T | can be neglected and T
0
≈ T . Furthermore,
Jokipii and Parker (1967) (see also [Jokipii and Parker (1970); Jokipii (1971)]) to
a first approximation demonstrated that for the number density [U(x
i
, T, t)] of the
cosmic-ray particles with kinetic energy T in the heliocentric frame and T
0
in the
moving frame we have
U(x
i
, T, t) ≈ U(x
i
, T
0
, t).
As a consequence, Eq. (4.35) can be rewritten as
∂U
∂t
−
∂
∂x
i
µ
K
i,j
∂U
∂x
J
¶
+
∂
∂T
µ
U
dT
dt
¶
+
∂
∂x
i
(U v
w,i
) = 0. (4.39)
‡
The distribution (i.e., the number density) of particles at the position ~r and time t is given
by [Parker (1965)]:
n(~r, t) ≡ n(x
i
, t) =
Z
∞
0
U(x
i
, T
0
, t) dT
0
.
¶
Parker (1965) demonstrated, in Appendix 6 of his article, that Fermi acceleration mechanism,
i.e., the stochastic energy gain which may occur in collisions with plasma clouds, provides a
negligible energy change.
‡‡
This occurs when the cosmic-ray particle moves along the direction of the solar wind.
∗
This is the kinetic-energy range of CRs in which the solar modulation i) affects their propagation
and ii) can be expressed by means of Eq. (4.35).
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
322 Principles of Radiation Interaction in Matter and Detection
For a radial SW with speed v
w
and an isotropic diffusion coefficient
k
K, the ap-
propriate distribution function, U(r, T, t), at heliocentric distance r is a spherically
symmetric modulated number density of CR particles with kinetic energy T . This
function can be obtained as the solution of the Fokker-Plank equation (4.39), by
rewriting this latter in spherical coordinates in which the helio-latitude and helio-
longitude dependencies vanish, i.e.,
∂U
∂t
= +
1
r
2
·
∂
∂r
µ
r
2
K
∂U
∂r
¶¸
+
1
3r
2
·
∂
∂r
¡
r
2
v
w
¢
¸·
∂
∂T
(α
rel
T U)
¸
−
1
r
2
·
∂
∂r
¡
r
2
v
w
U
¢
¸
, (4.40)
where α
rel
is given by
α
rel
=
T + 2m
r
c
2
T + m
r
c
2
=
(γ − 1) m
r
c
2
+ 2m
r
c
2
(γ − 1) m
r
c
2
+ m
r
c
2
=
γ + 1
γ
; (4.41)
m
r
is the rest mass of the CR particle and γ is its relativistic Lorentz factor (e.g., see
Sect. 1.3). Furthermore, we can express α
rel
T as:
α
rel
T =
µ
T + 2m
r
c
2
T + m
r
c
2
¶
T
=
µ
E
t
+ m
r
c
2
E
t
¶
¡
E
t
− m
r
c
2
¢
=
E
2
t
− m
2
r
c
4
E
t
(4.42)
=
p
2
p
E
t
(4.43)
= β
2
γm
r
c
2
, (4.44)
where E
t
is the total particle-energy [Eq.(1.12)] and p
p
is the particle momen-
tum. Furthermore, K is a phenomenological diffusion coefficient, which is assumed
to be isotropic, as already mentioned, and a function of the particle velocity, particle
rigidity and heliocentric distance. The first term on the right-hand side of Eq. (4.40)
describes the diffusion of GCRs by magnetic irregularities; the second
§
accounts for
the so-called adiabatic energy changes associated with expansions and compressions
of the cosmic radiation due to the i) geometrical (radial) divergence proportional
k
This corresponds to the assumption K
⊥
≈ K
k
and to neglect the antisymmetric part in
Eq. (4.58).
§
The cosmic-ray particle is cooled adiabatically and, neglecting Fermi mechanism acceleration
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Radiation Environments and Damage in Silicon Semiconductors 323
to 2v
w
/r and ii) acceleration or deceleration (i.e., when ∂v
w
/∂r 6= 0) of the SW;
the third is related to the resulting convection effect [Parker (1965); Gleeson and
Axford (1967); Jokipii and Parker (1970)]. Equation (4.40) can be rewritten with
the term
∂U
∂t
= 0,
if steady-state modulation conditions are appropriate, i.e., when the relaxation time
of the distribution is short compared with the solar cycle duration (as it is often
the case). The presence of any particle source, for instance that for anomalous
CRs (Sect. 4.1.2.4), is accounted by adding a term Q(r, T, t ) to the right-hand side
of Eq. (4.40) [Jokipii (1971); Potgieter (1998)] (see also references therein).
Furthermore, Gleeson and Axford (1967) demonstrated that Eq. (4.40) [origi-
nally derived by Parker (1965)] can be obtained by using a Legendre expansion of
the collision term of the Boltzmann equation and eliminating the so-called radial
current density term (also termed streaming term) S(r, T, t) from the resulting set
of Eqs. (4.45, 4.46):
∂U
∂t
= −
1
r
2
·
∂
∂r
¡
r
2
S
¢
¸
−
v
w
3
·
∂
2
∂T ∂r
(α
rel
T U)
¸
, (4.45)
S(r, T, t) = v
w
U −
v
w
3
·
∂
∂T
(α
rel
T U)
¸
− K
∂U
∂r
(4.46)
= C(r, T, t) v
w
U − K
∂U
∂r
, (4.47)
where
C(r, T, t) = 1 −
1
3U
·
∂
∂T
(α
rel
T U)
¸
(4.48)
is the so-called Compton–Getting factor
‡
. The streaming term
¶
represents the radial
current density for CR particles with kinetic energy T . Equation (4.45) can be
effects, it can be shown that its kinetic energy T declines as:
dT
dt
= −
T α
rel
3
∂v
w,i
∂x
i
= −
T α
rel
3
(∇ ·~v
w
)
(e.g., see [Parker (1965); Jokipii and Parker (1967, 1970)]). Thus, for a radial SW with speed v
w
we have
dT
dt
= −
T α
rel
3r
2
∂
∂r
¡
r
2
v
w
¢
.
‡
This Compton–Getting effect deals with the transformation of the differential mean density and
current density between reference frames moving relative to each other with constant velocity. Glee-
son and Axford (1968a) demonstrated that the Compton–Getting effect results in introducing the
Compton–Getting factor [Eq. (4.48)] in the streaming term [Eq. (4.47)].
¶
It is related to the number of particles with speeds between v and v + dv which cross a unit area
perpendicular to a unit vector direction in unit time [Gleeson and Axford (1968a)].

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
324 Principles of Radiation Interaction in Matter and Detection
rewritten in terms of the Compton–Getting factor using Eqs. (4.47, 4.48), i.e.,
∂U
∂t
= −
1
r
2
½
∂
∂r
·
r
2
µ
C v
w
U − K
∂U
∂r
¶¸¾
−
v
w
3
·
∂
2
∂T ∂r
(α
rel
T U)
¸
=
1
r
2
·
∂
∂r
µ
r
2
K
∂U
∂r
¶¸
−
1
r
2
·
∂
∂r
¡
r
2
C v
w
U
¢
¸
−
v
w
3
·
∂
2
∂T ∂r
(α
rel
T U)
¸
=
1
r
2
·
∂
∂r
µ
r
2
K
∂U
∂r
¶¸
−
v
w
3
·
∂
2
∂T ∂r
(α
rel
T U)
¸
−
CU
r
2
·
∂
∂r
¡
r
2
v
w
¢
¸
− v
w
·
∂
∂r
(C U)
¸
=
1
r
2
·
∂
∂r
µ
r
2
K
∂U
∂r
¶¸
−
v
w
3
·
∂
2
∂T ∂r
(α
rel
T U)
¸
−
CU
r
2
·
∂
∂r
¡
r
2
v
w
¢
¸
− v
w
½
∂U
∂r
−
1
3
·
∂
2
∂T ∂r
(α
rel
T U)
¸¾
=
1
r
2
·
∂
∂r
µ
r
2
K
∂U
∂r
¶¸
− v
w
∂U
∂r
−
CU
r
2
·
∂
∂r
¡
r
2
v
w
¢
¸
. (4.49)
Furthermore, the modulation of CRs can also be described by means of the so-called
omnidirectional distribution function
∗
f(~r, ~p
p
, t) of CR particles with momentum
~p
p
, at the position ~r and time t (e.g., see [Fisk, Forman and Axford (1973); Fisk
(1976)]). Forman (1970) derived that the Compton–Getting factor is given by
C
p
= −
p
p
3 f
∂f
∂p
p
= −
1
3f
∂f
∂ ln p
p
, (4.50)
where f is the omnidirectional distribution function averaged over particle direc-
tions. Thus, Eq. (4.49) can be rewritten as
∂f
∂t
=
1
r
2
·
∂
∂r
µ
r
2
K
∂f
∂r
¶¸
− v
w
∂f
∂r
−
C
p
f
r
2
·
∂
∂r
¡
r
2
v
w
¢
¸
=
1
r
2
·
∂
∂r
µ
r
2
K
∂f
∂r
¶¸
− v
w
∂f
∂r
+
1
3r
2
·
∂
∂r
¡
r
2
v
w
¢
¸µ
∂f
∂ ln p
p
¶
. (4.51)
∗
The omnidirectional distribution of particles with momentum ~p
p
at the position ~r and time t is
related to the differential intensity
h
J
³
~r, T,
~p
p
p
p
, t
´i
of particles with kinetic energy T traveling in
the direction ~n = ~p
p
/p
p
by
J
µ
~r, T,
~p
p
p
p
, t
¶
= p
2
p
f(~r, ~p
p
, t)
(see Equation (A3) of [Forman (1970)]), where m
r
is the rest mass of the particle;
Z
f(~r, ~p
p
, t) dp
p,x
dp
p,y
dp
p,z
= n(~r, t) =
Z
U(~r, T, t) dT
with n(~r, t) the number density of particles; finally, for the kinetic energy (T ) the following non-
relativistic expression is assumed
dT =
p
p
m
r
dp
p
.
Furthermore, taking into account that
dE
t
= dT
where E
t
is the total particle energy, the reader can also see the equivalence of the above definition
of differential intensity with that one expressed in Eq. (4.53).
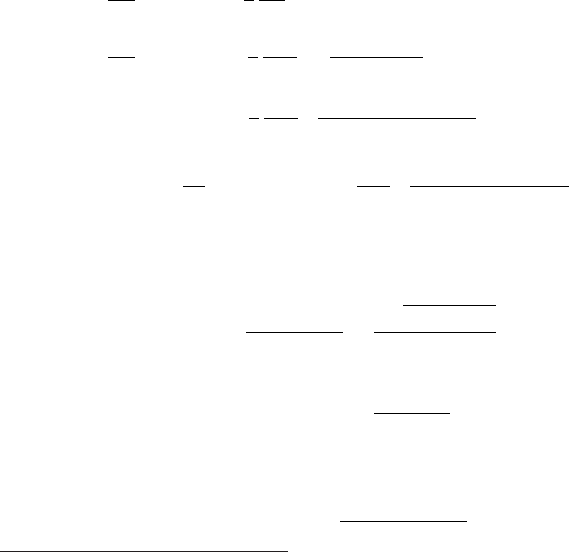
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Radiation Environments and Damage in Silicon Semiconductors 325
For a radial SW and an isotropic diffusion coefficient, this equation describ es the
SW modulation effect by means of the omnidirectional distribution function (f),
while Eq. (4.40) by means of the number density (U) of CR particles with kinetic
energy T .
When there are no sources or sinks at r = 0 and for steady modulation condi-
tions, Gleeson and Axford (1968b) estimated that, to a first approximation, the
streaming term, S, is negligible when
¶
T ≥ 400 MeV/nucleon for protons and
T ≥ 200 MeV/nucleon for α-particles at 1 AU, provided that the radial length cha-
racteristic of the radial variation of the diffusion coefficient is ≤ 1 AU. Furthermore,
this latter coefficient was assumed to be given by a separable function of r and R
p
isot
:
K(r, t) = βk
1
(r, t)k
2
(R
p
, t),
where R
p
is the particle rigidity [Eq. (4.71)], β = v/c, v is the particle velocity and
c is the speed of light; K(r, t) was estimated to be ≈ 10
22
cm
2
/s for particles of a
few GeV/nucleon. It has to be noted that above 1 GV k
2
(R
p
, t) reduces usually to
the value of the particle rigidity and is expressed in units of GV (e.g., see [Gleeson
and Axford (1968b); Perko (1987)]). Using Eq (4.42), for S ≈ 0 we can rewrite
Eq. (4.46) in terms of the total particle-energy [E
t
, see Eq.(1.12)] and rest mass
(m
r
) as
K
∂U
∂r
≈ v
w
·
U −
1
3
∂
∂T
(α
rel
T U)
¸
⇒ K
∂U
∂r
= v
w
½
U −
1
3
∂
∂E
t
·µ
E
2
t
− m
2
r
c
4
E
t
¶
U
¸¾
= v
w
(
U −
1
3
∂
∂E
t
"
U
E
t
(E
2
t
− m
2
r
c
4
)
1/2
¡
E
2
t
− m
2
r
c
4
¢
3/2
#)
= −
v
w
3
¡
E
2
t
− m
2
r
c
4
¢
3/2
∂
∂E
t
"
U
E
t
(E
2
t
− m
2
r
c
4
)
1/2
#
, (4.52)
with U = U (r, E
t
), in the above equation. Gleeson and Axford (1968b) intro-
duced the differential intensity
∗
, also termed omnidirectional intensity (e.g., page
63 of [Jokipii (1971)]),
J(r, E
t
, t) =
vU(r, E
t
, t)
4 π
=
c
p
E
2
t
− m
2
r
c
4
4 πE
t
U(r, E
t
, t) (4.53)
and the modulation parameter (also termed modulation strength)
φ
s
(r, t) =
Z
r
tm
r
v
w
(r
0
, t)
3k
1
(r
0
, t)
dr
0
, (4.54)
where it is indicated with r
tm
the location beyond which the SW terminates. As-
suming that v
w
and k
1
are almost constant, Eq.(4.54) reduces to
φ
s
(r, t) ≈
v
w
(t) (r
tm
− r)
3k
1
(t)
(4.55)
¶
The reader can find the definition of kinetic energies per nucleon in Sect. 1.4.1.
∗
It expresses the differential CR particle flux per unit of energy and solid angle.
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
326 Principles of Radiation Interaction in Matter and Detection
and is usually expressed in units of GV: for instance, a typical weak modulation
condition at 1 AU occurs for φ
s
(1 AU) = (0.32–0.35) GV. φ
s
(r, t) (as well as k
2
) is
independent of the species of CR particles. Finally, they derived that the solution
of Eq. (4.52) is given by the expression
J(r, E
t
, t) = J(r
tm
, E
t
+ Φ
p
)
·
E
2
t
− m
2
r
c
4
(E
t
+ Φ
p
)
2
− m
2
r
c
4
¸
, (4.56)
where J(r
tm
, E
t
+ Φ
p
) is the undisturbed intensity beyond the SW termination. Φ
p
is completely determined by φ
s
(r, t), but i) depends on E
t
, ii) may be different
for each species, iii) accounts for mean energy-losses experienced by particles with
kinetic energy T at a location with radial distance r when they come from outside
the solar cavity to this location and, thus, iv) may be interpreted as similar to a
“potential energy”. This approximated solution for determining modulation effects
is termed force-field solution, while Φ
p
is called force-field energy-loss (e.g., see
[Gleeson and Axford (1968b); Gleeson and Urch (1971)]. When modulation is small
(i.e., Φ
p
¿ m
r
c
2
, T ; see [Gleeson and Axford (1968b); Gleeson and Urch (1971)]),
Gleeson and Axford (1968b) determined in addition that
Φ
p
=
ZeR
p
k
2
(R
p
, t)
φ
s
(r, t),
where Ze is the particle charge; thus, using Eqs. (4.44, 4.71) we obtain
Φ
p
=
βγm
r
c
2
k
2
(R
p
, t)
Z
r
tm
r
v
w
(r
0
, t)
3k
1
(r
0
, t)
dr
0
=
β
2
γm
r
c
2
3
Z
r
tm
r
v
w
(r
0
, t)
βk
2
(R
p
, t)k
1
(r
0
, t)
dr
0
=
α
rel
T
3
Z
r
tm
r
v
w
(r
0
, t)
K(r
0
, t)
dr
0
. (4.57)
For r = 0 and assuming K and v
w
almost constant, Eq. (4.57) yields
Φ
p
≈
α
rel
T v
w
r
tm
3K
,
i.e., the mean energy-loss estimated by Parker (1966), in this particular case, for a
particle with kinetic energy T after modulation. Numerical solutions of the sphe-
rically symmetrical Fokker–Plank equation [Eq. (4.40)] and its force-field approxi-
mate solutions were widely investigated (e.g., see [Gleeson and Axford (1968b); Fisk
(1971); Perko (1987)] and references therein); at present the modulation effects are
also studied using a stochastic simulation approach in order to solve Eq. (4.40) for
the transport of the local interstellar spectrum
k
(LIS) to 1 AU in steady-state appro-
ximation (e.g., see [Gervasi, Rancoita, Usoskin and Kovaltsov (1999)] and references
therein).
In Eq. (4.40), the SW modulation was assumed to affect the differential particle
spectrum in a spherically symmetric way resulting in an isotropic diffusion coef-
ficient K. However, observed directions of the anisotropies were used as evidence
k
Nowadays, the commonly used LIS is the one from [Burger and Potgieter (1989)].

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Radiation Environments and Damage in Silicon Semiconductors 327
supporting models for CRs propagation involving diffusion, which is primarily along,
and not across, the magnetic-field lines (e.g., see discussion in [Rao et al. (1971)]
and references therein): the typical ratio of the transverse (K
⊥
) to parallel (K
k
)
diffusion coefficient is
K
⊥
K
k
' 0.07
at 1 GV rigidity [Forman, Jokipii and Owens (1974)] (see also [Jokipii and Parker
(1970)] and references therein). The effects of anisotropy in the IMF can be treated
by retaining the anisotropic character of the diffusion coefficient as a diffusion
tensor K
i,j
, which, in a reference system with the 3rd coordinate along the average
magnetic-field, takes the simple form
∗
K
i,j
=
K
⊥
− K
A
0
K
A
K
⊥
0
0 0 K
k
; (4.58)
K
⊥
and K
k
are the transverse (or perpendicular) and parallel diffusion coefficients,
respectively, and originate the symmetric part of the diffusion tensor (K
s
). K
A
(also
termed drift diffusion coefficient) originates the antisymmetric part of the diffusion
tensor (K
a
), contains the effects of gradient and curvature drifts of the particles
in the average magnetic-field
~
B and, when the scattering mean free path is much
greater than the radius of gyration (r
g
) of the particle [Parker (1965); Jokipii (1971)],
is given by
K
A
=
1
3
v
p
r
g
B
z
|B
z
|
,
where v
p
is the particle velocity: if the magnetic field or the particle charge changes
sign, the sign of K
A
changes [Parker (1965); Jokipii and Parker (1970); Jokipii
(1971); Jokipii and Levy (1977); Jokipii, Levy and Hubbard (1977); Reinecke and
Potgieter (1994); Potgieter (1998)]. Jokipii (1971) remarked how the antisymmetric
part of the diffusion tensor does not contribute to the Fokker–Planck transport
equation, when the magnetic field is independent of the position (page 46 of [Jokipii
(1971)]); sometimes the antisymmetric part is neglected in the literature. Further-
more, it has to be noted that for the IMF pattern described by the Parker model,
the radial diffusion coefficient is given by:
K
r
= K
k
cos
2
ψ
sp
+ K
⊥
sin
2
ψ
sp
,
where ψ
sp
is the spiral angle {see Eq. (4.21) and [Jokipii and Parker (1970)]}.
By decomposing the diffusion tensor K
i,j
into its symmetric (K
s
i,j
) and antisym-
metric (K
a
i,j
) parts, Jokipii, Levy and Hubbard (1977) demonstrated that Eq. (4.39)
can be rewritten as (see also [Jokipii and Levy (1977)] and footnote at page 323):
∗
The reader can see, for instance, Equation (50) in [Jokipii (1971)], also, [Jokipii and Parker
(1970); Jokipii, Levy and Hubbard (1977)] and, in spherical coordinates, [Burger and Hattingh
(1998)].
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
328 Principles of Radiation Interaction in Matter and Detection
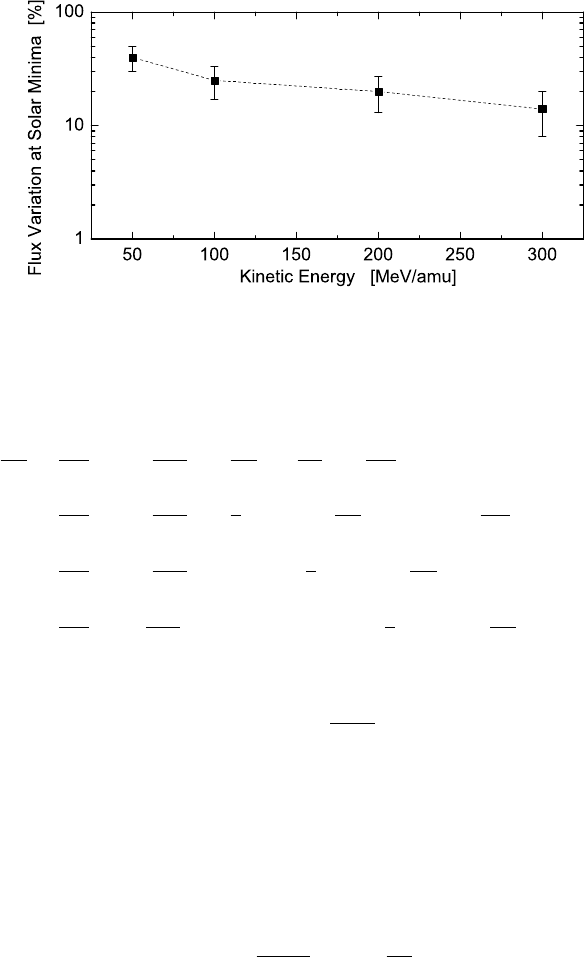
Fig. 4.10 Variation (in percentage) of proton and helium flux between two subsequent solar
minima with opposite solar magnetic-field polarities as a function of the particle kinetic-energy
(in MeV/amu): data from [Boella, Gervasi, Mariani, Rancoita and Usoskin (2001)]. The dashed
line is to guide the eye.
∂U
∂t
=
∂
∂x
i
µ
K
i,j
∂U
∂x
J
¶
−
∂
∂T
µ
U
dT
dt
¶
−
∂
∂x
i
(U v
w,i
)
=
∂
∂x
i
µ
K
i,j
∂U
∂x
J
¶
+
1
3
(∇ · ~v
w
)
·
∂
∂T
(α
rel
T U)
¸
−
∂
∂x
i
(U v
w,i
)
=
∂
∂x
i
µ
K
i,j
∂U
∂x
J
− U v
w,i
¶
+
1
3
(∇ · ~v
w
)
·
∂
∂T
(α
rel
T U)
¸
=
∂
∂x
i
µ
K
s
i,j
∂U
∂x
J
−U v
w,i
¶
−h~v
d
i · ∇U+
1
3
(∇ · ~v
w
)
·
∂
∂T
(α
rel
T U)
¸
, (4.59)
where the drift velocity is
hv
d,i
i =
∂K
a
i,j
∂x
j
.
The second term on the right-hand side of Eq. (4.59) is the so-called drift term and
describes the drift effects due to the SW (e.g., [Forman, Jokipii and Owens (1974);
Jokipii and Levy (1977); Kota and Jokipii (1983); Le Roux and Potgieter (1990);
Potgieter, Le Roux, Burlaga and McDonald (1993); Ferreira, Potgieter, Heber and
Fichtner (2003)] and references therein). For an IMF following an Archimedean
spiral pattern, the drift velocity can be approximated by
h~v
d
i =
p
p
v
p
c
3Ze
"
∇ ×
Ã
~
B
B
2
!#
, (4.60)
where Ze is the charge of the CR particle (e.g., see Equation 7.58 at page 274
of [Kallenrode (2004)] and [Potgieter and Moraal (1985)]). The drift velocity has
an opposite direction for i) opposite charge states when magnetic-field polarity (A)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Radiation Environments and Damage in Silicon Semiconductors 329
of the Sun is the same and ii) the same charge state when the Sun magnetic-field
polarity is reversed.
The charge-drift effect can be best observed when the solar activity is at mi-
nimum [Potgieter, Le Roux, McDonald and Burlaga (1993)]. For instance, the so-
lar modulation dependence on the sign of CR particles was observed by Garcia-
Munoz, Meyer, Pyle, Simpson and Evenson (1986). The charge dependence becomes
gradually ineffective with increasing solar activity, as observed using IMP8 satel-
lite data during the period 1973–1995 by Boella, Gervasi, Mariani, Rancoita and
Usoskin (2001); the effect exhibited its maximum strength at the solar minima: in
Fig. 4.10, it is shown the variation of proton and helium flux (in percentage)
1 − R = 1 −
Φ
−
Φ
+
=
Φ
+
− Φ
−
Φ
+
between two subsequent solar minima as a function of the kinetic energy
∗∗
(in
MeV/amu); Φ
+
and Φ
−
are the particles fluxes
k
for A > 0 and A < 0, resp ecti-
vely. The observed particle flux depletion decreases with increasing particle energy.
As discussed above, drift effects are expected to affect the modulation, helio-
centric gradient and energy change of CRs
‡‡
in the inner solar system [Jokipii and
Levy (1977); Garcia-Munoz, Meyer, Pyle, Simpson and Evenson (1986); Reinecke
and Potgieter (1994); Bieber and Matthaeus (1997); Boella, Gervasi, Mariani, Ran-
coita and Usoskin (2001)] (see also references in [Potgieter (1998)]). For instance,
when the Sun magnetic-field lines in the northern hemisphere are directed outwards
(e.g., for A > 0), the inclusion of drift effects [Jokipii and Thomas (1981)] are rel-
evant to account that positively charged particles drift inwards the polar regions
and outwards along the current sheet (see page 311); the sense of drift is reversed
when the magnetic-field polarity of the Sun is reversed (A < 0) (see [Isenberg and
Jokipii (1979); Jokipii and Thomas (1981)], Section 7.7.2 of [Kallenrode (2004)] and
references therein). As a function of the solar activity, these effects can be accounted
and, partially, estimated by means of computer simulations of CRs propagation in-
side the heliosphere (e.g., see [Potgieter, Le Roux, Burlaga and McDonald (1993);
Bobik et al. (2003, 2006a)]).
In addition, the actual requirements of simulating the space radiation environ-
ment are addressed by means of empirical or semi-empirical dynamical models of the
GCR modulation like, for instance, the Nymmik–Panasyuk–Pervaja–Suslov model
(e.g., see [Nymmik, Panasyuk, Pervaja and Suslov (1992); Nymmik and Suslov
(1996); ISO-15390 (2004)]). In this model at 1 AU beyond Earth’s magnetosphere,
the effective modulation potential of the heliosphere is the main parameter and
is calculated, at the time t, using the expression {see Equation (9) in [Nymmik,
∗∗
The reader can find a definition of kinetic energies per amu in Sect. 1.4.1.
k
These fluxes are observed at the solar minima and normalized to the same value of neutron
monitor counting rate registered at Climax Station (for a discussion about the normalization
procedure, the reader can see [Boella, Gervasi, Mariani, Rancoita and Usoskin (2001)]).
‡‡
Effects on modulated spectra can be relevant for particles with rigidities as large as 4 GV [Bieber
and Matthaeus (1997)].
