Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

460 Principles of Radiation Interaction in Matter and Detection

Voltage (volts)

Capacitance (pF)

100

200

10 10

Voltage (volts)

Capacitance (pF)

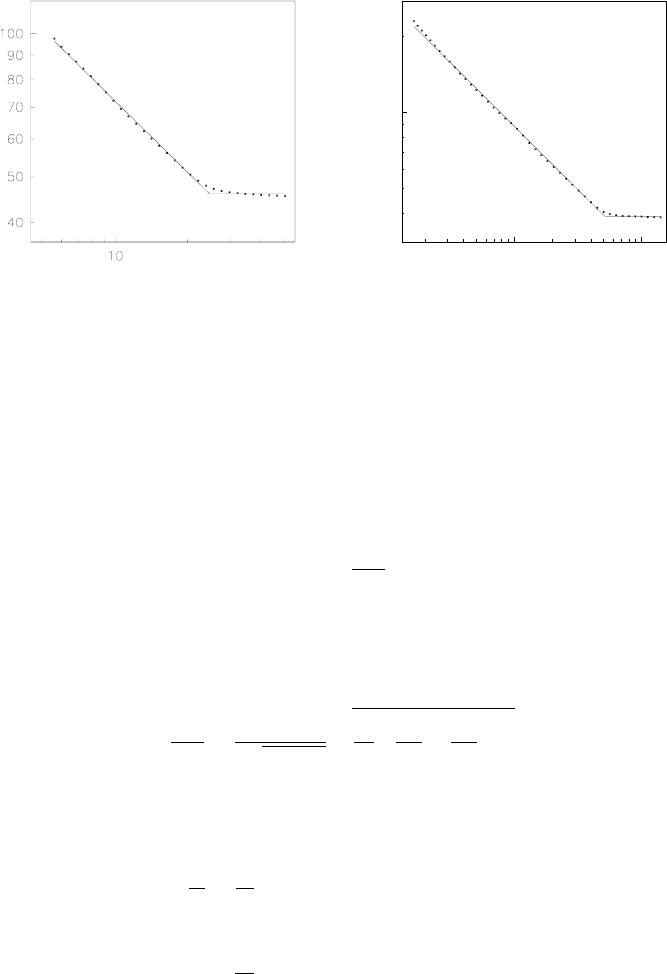
Fig. 6.3 Capacitance (in pF) curves as a function of applied voltage (in V) for two detectors of

1 cm

area [Leroy (1998)]: (a) resistivity of ρ = 8 kΩcm and thickness w = 247 µm; (b) resistivity

of ρ = 6 kΩcm and thickness w = 300 µm. The curve represents a ﬁt of Eq. (6.34) to the data

points.

the negative space charge). The opposite process is observed when the applied vol-

tage decreases, leading to free charge removal and to an increase of space-charge,

, in the transition region. The variation of Q

with voltage in the transition zone

has the dimension of a capacitance (C

), i.e.,

(6.31)

with Q

given by

= AqN

. (6.32)

From the Eqs. (6.29, 6.30), one obtains

√

+ V

2ε

−1

. (6.33)

Inserting Eq. (6.15) into Eq. (6.33), one recovers Eq. (6.28) describing the parallel

plate capacitor approximation, i.e., two parallel plates separated by a distance X

and C in Eq. (6.28) being obviously the same quantity]:

for 0 < X ≤ w (6.34)

and, consequently,

C = ε

for 0 < X ≤ w. (6.35)

The detector capacitance is minimal when X is maximal. This occurs when the

detector full depletion is achieved, i.e., when X = w. For applied voltage larger

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Solid State Detectors 461

0.5

1.5

2.5

3.5

0 20 40 60 80 100 120 140 160

V (volts)

Charge (fC)

0.5

1.5

2.5

3.5

024681012

1/2

(volts

1/2

)

Charge (fC)

Fig. 6.4 Charge collected with a silicon detector 300 µm thick, area 1 cm

, exposed to incoming

electrons of energy larger than 2 MeV, as a function of the applied bias (a) and as a function of

the square root of the applied voltage (b). The value of the full depletion voltage is 60 volts which

corresponds to a collected charge of 3.5 fC, as expected from the most probable energy deposited

by relativistic electrons in this detector [Leroy (1998)].

than V

, the capacitance remains constant and a plateau is observed (Fig. 6.3). An

estimate of the full depletion voltage can be obtained by taking the value of voltage

corresponding to the intersection of the C − V curve with the line of constant

geometrical capacitance. The depletion voltage decreases with increasing resistivity,

as already observed. The capacitance at full depletion of the 1 cm

area detectors

shown in Fig. 6.3 is obtained applying Eq. (6.28): one ﬁnds 42.5 pF [thickness

w = 247 µm, Fig. 6.3(a)] and 35.0 pF [thickness w = 300 µm, Fig. 6.3(b)].

Furthermore, the measurement of capacitance as a function of the applied

bias voltage allows the determination of the full depletion voltage and N

eﬀ

2ε/qw

), from Eq. (6.24) where V

has been neglected. As will be seen in

Sect. 6.1.4, the full depletion bias voltage can also be obtained from charge col-

lection measurements. C − V measurements permit the determination of N

eﬀ

a function of the depth X of the depletion layer, i.e., the N

eﬀ

proﬁle. Combining

Eqs. (6.24, 6.34) (where V = V

+ V

), one ﬁnds:

eﬀ

(X) =

qεA

d(1/C

)

. (6.36)

6.1.4 Charge Collection Measurements

Let us turn to the study of the energy deposited by relativistic electrons

∗

in silicon

detectors of current use. Since these detectors are thin (a few hundreds microns,

typically), the energy deposited by minimum ionizing particles (mip) in these silicon

detectors follows a Landau-type spectrum. The most probable energy deposition by

∗

The energy deposited by relativistic electrons is similar to the energy deposited by minimum

ionizing particles (see Sect. 2.1.6.1).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

462 Principles of Radiation Interaction in Matter and Detection

a mip is about 80 keV per 300 µm of silicon. If one takes into account the ionization

energy E

ion

= 3.62 eV, that corresponds to about 22,000 electron-hole pairs created

per 300 µm of silicon. Then, a charge of 22, 000 ×1.6 ×10

−19

C = 3.5 fC is released

per 300 µm of silicon. An example is shown in Fig. 6.4(a) where the collected charge

as a function of the applied bias voltage is shown for a silicon detector 300 µm thick

exposed to relativistic electrons (of energy larger than 2 MeV). Figure 6.4(b) shows

the collected charge as a function of V

1/2

for the same detector exposed to the

same incoming electron beam. In agreement with Eqs. (6.22) or (6.26), it can be

observed that the detector signal (collected charge) has a square root dependence

on the bias voltage b elow the full depletion voltage and is constant (Q = 3.5 fC) as

a function of V above it. The measurement of the collected charge as a function of

the applied bias voltage is a way to determine the value of the full depletion voltage

), i.e., the value of voltage for which a value of the collected charge constant

with voltage begins to be observed. For the example shown is Fig. 6.4, the plateau

starts at V

∼ 60 V.

The mean charge collection

†

is proportional to the detector thickness. Figure 6.5

shows the mean charge collection from relativistic electrons (E

> 2 MeV) for fully

depleted detectors of various thicknesses [(142–996) µm]. The average energy de-

position is ∼ (2.70 ± 0.04) × 10

eV µm

−1

, in agreement with the expected energy

deposition for relativistic electrons.

6.1.5 Charge Transport in Silicon Diodes

The movement of the charge carriers generated by an ionizing particle in a detector

produces a signal which shape is determined by the charge transport properties

of the detector. The charge transport properties of the diode are governed by its

electrical characteristics: i) the eﬀective concentration of dopants (N

eﬀ

), which

deﬁnes the internal electric ﬁeld and, thus, the depletion voltage, ii) the electron

(µ

) and hole (µ

) mobilities, which inﬂuence the time needed to collect the charge

and iii) the charge trapping lifetime (τ

, τ

), which aﬀects the eﬃciency of the

charge collection. First, let us assume a simpliﬁed model where the electron and

hole mobilities are constant with the electric ﬁeld. The electric ﬁeld inside the

depleted region of the detector can be expressed as [Lemeilleur et al. (1994)]:

E(x) = −

eﬀ

(x − w) +

− V

= −ax + b, (6.37)

where V

is the applied bias voltage, V

is the full depletion voltage,

b ≡

wqN

eﬀ

− V

and a =

eﬀ

Ramo’s theorem [Ramo (1939)] relates the displacement (∆x) of a charge carrier

generated by the passage of an incoming particle in the detector to the charge (∆q)

†

The reader may refer to Sects. 2.1.1, 2.1.6.1 for a further discussion.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Solid State Detectors 463

0 200 400 600 800 1000

thickness (microns)

collected charge (fC)

Fig. 6.5 Mean charge collection (fC) for relativistic electrons from a

106

Ru source (with E

2 MeV) as a function of the detector thickness (142–996 µm). The line is to guide the eye (reprinted

from Nucl. Instr. and Meth. in Phys. Res. A 479, Bechevet, D., Glaser, M., Houdayer, A., Lebel,

C., Leroy, C., Moll, M. and Roy, P., Results of irradiation tests on standard planar silicon detectors

with 7–10 MeV protons, 487–497, Copyright (2002), with permission from Elsevier).

that it induces on the electro des:

∆q = q

∆x

. (6.38)

The induced current at the electrode is given by

i(x) =

v(t), (6.39)

where

v(t) = v

(t) =

= µ

E(x) = µ

(−ax + b), (6.40)

for electrons, and

v(t) = v

(t) =

= µ

E(x) = −µ

(−ax + b) (6.41)

for holes; µ

and µ

are the electron and hole mobility, respectively. Integrating

Eqs. (6.40, 6.41) over time for a unit charge generated at x = x

gives

(t) =

−

exp(−µ

at), (6.42)

and

(t) =

−

exp(µ

at), (6.43)

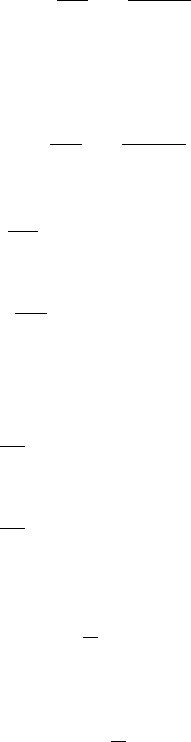
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

464 Principles of Radiation Interaction in Matter and Detection

with the corresponding electron and hole velocities:

(t) = −µ

(ax

− b) exp(−µ

at) (6.44)

and

(t) = µ

(ax

− b) exp(µ

at). (6.45)

The electron collection time (t

coll

), i.e., the time taken by the electron generated at

x = x

to reach the electrode located at x = w, is given by

coll

(e) = −

aw − b

− b

. (6.46)

In the same way a hole collection time can deﬁned, while the electron generated

at x = x

is drifting towards the electrode at x = w, the hole drifts in opposite

direction from x = x

to x = 0 during the time:

coll

(h) =

−b

− b

. (6.47)

The current induced by electrons (i

) and holes (i

) at the electrodes is given by:

(t) =

qµ

(ax

− b) exp(−µ

at), (6.48)

for 0 ≤ t ≤ t

coll

(e), and

(t) =

qµ

(ax

− b) exp(µ

at), (6.49)

for 0 ≤ t ≤ t

coll

(h).

The integration of the currents over time gives the electron and hole collected

charge:

(t) = −

(ax

− b) [exp(−µ

at) − 1] , (6.50)

for 0 ≤ t ≤ t

coll

(e), and

(t) =

(ax

− b) [exp(µ

at) − 1] , (6.51)

for 0 ≤ t ≤ t

coll

(h). The total electron collected charge is obtained by integrating

Eq. (6.50) over time

tot

(e) =

(w − x

), (6.52)

while the total hole collected charge is obtained from the integration of Eq. (6.51)

over time:

tot

(h) =

. (6.53)

Summing Eqs. (6.52, 6.53), we get a total collected charge of

tot

= q, (6.54)

i.e., the unit charge initially injected.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Solid State Detectors 465

(x)

p+n

Back Front

min max

E(x)

− ψ (x)

Fig. 6.6 (a) Representation of a p

− n −n

dio de (over-depleted), (b) the dopant density

proﬁle ρ, (c) the electric ﬁeld E and (d) the electrostatic potential ψ (reprinted from Nucl.

Instr. and Meth. in Phys. Res. A 479, Bechevet, D., Glaser, M., Houdayer, A., Lebel,

C., Leroy, C., Moll, M. and Roy, P., Results of irradiation tests on standard planar sili-

con detectors with 7–10 MeV protons, 487–497, Copyright (2002), with permission from

Elsevier).

A more complete treatment of the charge transport problem is presented be-

low. In that case, the mobility will be expressed as a function of the electric ﬁeld

and of other parameters. A planar silicon diode (p

−n − n

) is assumed with the

junction and ohmic side located at x = 0 et x = w, respectively. Figure 6.6 gives a

schematic view of the junction under consideration. These electrical characteristics

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

466 Principles of Radiation Interaction in Matter and Detection

are extracted by solving in one-dimension (through the use of a transverse diﬀusion

term) a system of ﬁve partial diﬀerential equations with space (x) and time (t)

variables ([Leroy, Roy, Casse, Glaser, Grigoriev and Lemeilleur (1999a)] for more

details). A single trap state is assumed. Equation (6.7) is rewritten as:

∇

ψ = −∇E = −

(−N

eﬀ

− n + p − n

+ p

), (6.55)

n (p) is the free electron (hole) density while n

) is the trapped electron (hole)

density. The diﬀerence p − n in Eq. (6.55) accounts for possible plasma eﬀects,

when the electron and hole densities are of the order of the eﬀective concentration

of dopants. The carriers are thus shielding themselves from the external electric

ﬁeld and take a longer time to be collected.

500

600

700

800

900

1000

1100

1200

1300

0123456

dE⁄dx (MeV cm

-1

)

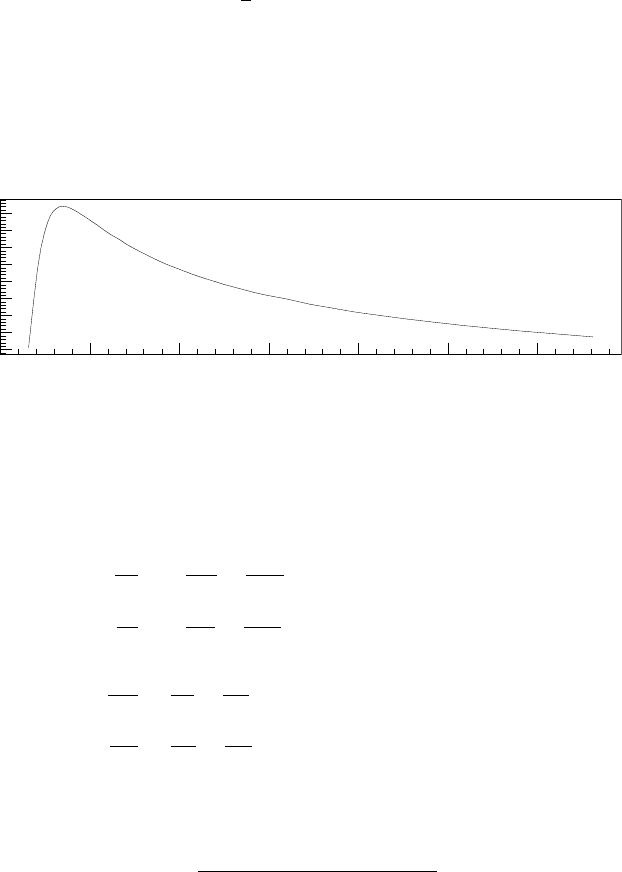
Fig. 6.7 Energy deposition of an alpha-particle in silicon (reprinted from Nucl. Instr. and Meth.

in Phys. Res. A 479, Bechevet, D., Glaser, M., Houdayer, A., Lebel, C., Leroy, C., Moll, M. and

Roy, P., Results of irradiation tests on standard planar silicon detectors with 7–10 MeV protons,

487–497, Copyright (2002), with permission from Elsevier).

The system of equations involves two continuity equations for electrons and

holes:

∂n

∂t

= −

∂n

∂t

∇J

+ g − Rn − U

SRH

∂p

∂t

= −

∂p

∂t

−

∇J

+ g − Rp − U

SRH

, (6.56)

∂n

∂t

−

− Rn

∂p

∂t

−

− Rp

, (6.57)

where g is the electron–hole pair generation function, τ

te/h

and τ

de/h

are the

trapping and de-trapping times, respectively; U

SRH

is the Shockley–Read–Hall

generation-recombination term

SRH

np − n

int

(p + n

int

)τ

+ (n + n

int

)τ

. (6.58)

The current densities of carriers densities are given by:

= qnµ

E + µ

T ∇n,

= qpµ

E − µ

T ∇p, (6.59)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Solid State Detectors 467

where k

and T are the Boltzmann constant and the temperature, respectively; µ

and µ

are the electron and hole mobilities, respectively. These mobilities depend

on the electric ﬁeld (E) and the temperature (T ). The system of equations reﬂects a

cylindrical symmetry as the induced charges are generated inside a cylinder and are

transversely diﬀused with time. In Eqs. (6.56, 6.57), this is accounted by the term

R [Taroni and Zanarini (1969)], which takes into account the transverse diﬀusion

of charge carriers:

R =

18D

t + r

, (6.60)

where r

is the initial radius of the column of deposited charge, the radius of the

column at a time t b eing

(t) = 18 D

t + r

;

is the ambipolar diﬀusion coeﬃcient and can be expressed as

+ D

, (6.61)

where

(6.62)

are the Einstein relations (c = e, h). Values of the diﬀusion coeﬃcients, D

(c =

e, h), are given at page 487. It has to be noted that the minority carrier diﬀusion

length for electrons in p-type material is given by

(6.63)

and for holes in n-type material is given by

, (6.64)

where τ

and τ

are the electron and hole carrier lifetime, respectively.

When neglecting the size of the p

and n

regions, the integration of the one-

dimensional Poisson’s equation at t = 0, for a simple abrupt p−n junction operated

in over-depleted mode (V

> V

), gives

E(x, 0) = −

eﬀ

x +

eﬀ

w |N

eﬀ

, for 0 < x < w (6.65)

with the boundary conditions:

E(0, t) = E(w, t) = 0, (6.66)

ψ(0, t) = V

+ ψ

≈ 0 and ψ(w, t) = ψ

− V

≈ −V

, (6.67)

where ψ and E are the electrostatic potential and the electric ﬁeld, respectively; q,

² and w are the electrical charge, the silicon electric permittivity and the thickness

of the diode, respectively; V

≈ 0.6 V is the built-in voltage, V

is the applied bias

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

468 Principles of Radiation Interaction in Matter and Detection

100

200

300

400

500

0246810

Electric field (kV/cm)

Holes mobility (cm

/Vs)

200

400

600

800

1000

1200

1400

0246810

Electric field (kV/cm)

Electrons mobility (cm

/Vs)

Fig. 6.8 Hole (left) and electron (right) mobility (cm

−1

) as a function of the electric ﬁeld

(kV/cm), Eq. (6.69), (reprinted from Nucl. Instr. and Meth. in Phys. Res. A 479, Bechevet,

D., Glaser, M., Houdayer, A., Lebel, C., Leroy, C., Moll, M. and Roy, P., Results of irradiation

tests on standard planar silicon detectors with 7–10 MeV protons, 487–497, Copyright (2002), with

permission from Elsevier).

voltage, ψ

(−0.6 ≤ ψ

≤ −0.3 V) is the electrostatic potential of the neutral p-type

region and V

is the full depletion bias voltage.

For a relativistic β particle in silicon, the range exceeds the physical size of

the detector and a uniform density of electron–hole pairs is created with n

≈

80 pairs/µm.

The generation function, g in Eq. (6.56, 6.57) at time t = 0 is given by:

g(x) =

× density(x) δ(x − x

)

density(x

)

with x

min

≤ x

max

. (6.68)

For an α particle of 5.0 MeV in silicon, the number of electron–hole pairs created

is n

≈ 1.4 million pairs over a range

r = x

max

− x

min

≈ 25 µm,

while the density of the electron–hole pairs is obtained by interpolation of the data

from [Williamson, Boujot and Picard (1966)] shown in Fig. 6.7.

The drift velocity of the charge carrier reaches a saturation value v

for elec-

tric ﬁeld values around 10

V/cm [Dargys and Kundrotas (1994)]. The empirical

equation describing the mobility as a function of the electric ﬁeld is:

µ(x) =

[1 + (µ

E(x)/v

)

]

1/m

, (6.69)

where µ

is the zero ﬁeld mobility, m = 1 for holes, m = 2 for electrons; v

1.05×10

and 10

cm/s for electrons and holes, respectively [Dargys and Kundrotas

(1994)]. The dependence of the mobilities on the electric ﬁeld is shown in Fig. 6.8

for holes (left) and electrons (right).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Solid State Detectors 469

Table 6.1 Examples [Leroy, Roy, Casse, Glaser, Grigoriev and Lemeilleur

(1999a); Roy (2000)] of characteristics of the standard planar silicon detectors

of current use.

Detector Current thickness |N

eﬀ

| ρ

(area) pulse source (µm) (×10

−3

) (kΩ cm)

M4 (1 cm

) α 317 3.4 12.2

M18 (1 cm

) α,β 309 4.1 11.0

M25 (1 cm

) α,β 308 2.1 23.0

M35 (1 cm

) α 508 1.7 24.0

M49 (1 cm

) β 301 4.7 8.9

M50 (1 cm

) β 471 1.8 22.8

M53 (1 cm

) β 223 5.4 7.7

P88 (0.25 cm

) α,β 290 18.0 2.5

P189 (0.25 cm

) α,β 294 18.0 2.5

P304 (0.25 cm

) α,β 320 7.0 6.0

The mobilities also depend on the temperature and dopant concentra-

tions [Caughey and Thomas (1967)]. The eﬀect of concentration is only appreciable

for concentrations over 10

dopants/cm

. Changing the temperature by 1.5 degree

Celsius changes both mobilities by ≈ 1%. These features are taken into account via

the empirical equation

µ(T, N

eﬀ

) = µ

min

(T/300)

− µ

min

1 + (T /300)

eﬀ

ref

)

, (6.70)

where the values used for the electrons (holes) are: µ

min

= 55.24 (49.7) cm

−1

ref

= 1.072 × 10

(1.606 × 10

) dopants/cm

, ν = −2.3 (−2.2), ξ = −3.8

(−3.7), α = 0.73 (0.70), T is the temperature in kelvin and µ

is the mobility at

T = 300 K. The temperature dependence of mobility is shown in Fig. 6.9 using

(for e) = 1350 cm

−1

and µ

(for h) = 480 cm

−1

at T = 300 K.

As a consequence of Ramo’s theorem [Eq. (6.38)], the observed signal, V (t), is a

convolution of the current, I(t), produced by all the individual charge carriers and

the response from the system, which is simply an RC circuit. The response of the

system is a Gaussian with a characteristic time constant σ = R

C, where C is the

capacitance of the detector and R

the input impedance of the ampliﬁer:

I(t) =

18D

t + r

w r

(µ

n + µ

p)E dx, (6.71)

V (t) =

√

2π

e,h

∞

−∞

I(t

) exp

−

(t − t

)

2σ

, (6.72)

where D

is the ambipolar diﬀusion constant [Eq. (6.61)], G the gain of the ampliﬁer

and r

the initial radius of the column of deposited charge.

As an example, a simple case will be examined where silicon diodes are exposed

to electrons from a

106

Ru source with an energy > 2 MeV, selected by an external

trigger, and to α-particles from an

241

Am source with an energy of 5.49 MeV. The

setup for measuring the charge induced by the charge carriers generated by

106