Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

▶ Palm Vein recognition

▶ Vein and Vascular recognition

References

1. Time.com: www.time.com/time/printout/0,8816,755453,00.html

2. Jain, A., Ruud, B., Sharath, P. et al.: Biometrics personal Identi-

ﬁcation in Network Society, pp. 123–141. Kluwer Academic

Publishers, Dorrecht (1999)

3. Ruud, M.B., Jonathan, H.C., Sharath, P., Nalini, K.R., Andrew,

W.S.: Guide to Biometrics, pp. 53–54. Springer, Heidelberg

(2004)

4. Nanili, K.R., Venu, G.: Advances in Biometrics Sensor, Algo-

rithms and Systems, pp. 133–155. Springer, Heidelberg (2008)

Retinal Angiogenesis

The formation of retina blood vessels by budding or

sprouting from existing vessels. Random processes

during retinal angiogenesis are thought to be responsi-

ble for the unique nature of the retinal blood vessel

network.

▶ Simultaneous Capture of Iris and Retina fo r

Recognition

Retinal Blood Vessels

The retina receives blood from two sources, the cho-

roidal capillaries and the central retinal artery. The

retinal and choroidal blood vessel pattern is unique

to every person. The branches of the central artery and

vein, for instance, diverge from the optic disc in a

distinctive pattern that varies considerably across indi-

viduals. These retinal blood vessels are readily visible

on a regular fundus photograph taken with visible

light, whereas the choroidal blood vessels, forming a

matting behind the retina, become visible when ob-

served with near-infrared illumination.

▶ Anatomy of Eyes

Retinal Scan

▶ Retina Recognition

Reverse Engineering

Reverse Engineering refers mechanical disassembling

and software analysis for architectural parsing for

product to study/investigate operational mechanisms

and its source code, etc.

▶ Embedded Systems

Revocable Biometrics

▶ Cancelable Biometrics

Ridge Enhancement

▶ Fingerprint Image Enhancement

Ridge Extraction

▶ Fingerprint Image Enhancement

Ridge Flow

The direction and overall pattern of a group of ridges

in an area of friction ridge skin.

▶ Anatomy of Friction Ridge Skin

1130

Retinal Angiogenesis

Robustness Test

Test to evaluate how much a certain inﬂuencing factor

can affect biometric performance is robustness test.

▶ Influential Factors to Performance

ROC Curve

An ROC (receiver operating characteristic) curve is a

plot commonly used in machine learning and data

mining for exhibiting the performance of a classiﬁer

under different criteria. The y-axis is the true positive

and the x-axis is the false positive (i.e., false alarm).

A point on ROC curve shows that the trade-off be-

tween the achieved true positive detection rate and

the accepted false positive rate.

▶ Face Detection

▶ Performance Measures

Rolled-Equivalent Fingerprint

It refers to a special impression of the ﬁngerprint

obtained by rolling the ﬁnger around the main ﬁnger

axis on a planar surface.

▶ Fingerprint, Palmprint, Handprint and Soleprint

Sensor

Rolls Capture Device

It refers to a ﬁngerprint device that allows the capture

of rolled equivalent ﬁngerprints. A special reconstruc-

tion algorithm is needed to compose the ﬁngerprint

during the rolling of the ﬁnger on the surface.

▶ Fingerprint, Palmprint, Handprint and Soleprint

Sensor

Rotation Angle

The rotation angle is the angle between the line joining

the left and right pupil centers and the hor izontal axis

of the iris camera system. Counterclockwise rotation of

the head about the optical axis of the camera is consid-

ered positive and clockwise rotation is considered

negative.

▶ Iris Image Data Interchange Formats, Standardization

▶ Pose

Rotation Angle

1131

Sample Quality

The intrinsic characteristic of a biometric signal may

be used to determine its suitability for further proces-

sing by the biometric system or to assess its confor-

mance to preestablished standards. The quality of a

biometric signal is a numerical value (or a vector)

that measures this intrinsic attribute (See also

▶ Bio-

metric Sample Qu ality).

▶ Biometric Algorithms

▶ Fusion, Qualit y-Based

Sample Size

▶ Manifold Learning

▶ Performance Evaluation, Overview

▶ Test Sample and Size

Sampling Frequency

Sampling frequency is the number of sam ples captured

in a second from the continuous hand-drawn signal to

generate a discrete signal.

▶ Digitizing Table t

Scalability

Scalability is the ability of a biometric system to extend

adaptively to larger population without requiring

major changes in its infrastructure.

▶ Performance Evaluation, Overview

Scenario Tests

Scenario tests are those in which biometric systems

collect and process data from test subjects in a speci-

ﬁed application. An essential characteristic of scenario

testing is that the test subject is ‘‘in the loop,’’ inter-

acting with capture devices in a fashion representative

of a target application. Scenario tests evaluate end-

to-end systems, inclusive of capture device, quality

validation software, enrollment software, and match-

ing software.

▶ Performance Testing Methodology Standardization

Scene Marks

Crime scene marks are generally any physical phenom-

enon created or left behind and in relation to a crime

scene, these can be ﬁngerprints, blood spatter,

2009 Springer Science+Business Media, LLC

intentional and unintentional damage, or alteration to

objects in the environment of the crime.

▶ Footwear Recognition

Scent Identification Line-Ups

Procedure where a trained dog matches a sample odor

provided by a person to its counterpart in an array (or

line-up) of odors from different people , following a

ﬁxed protocol. Scent identiﬁcation line-ups are used in

forensic investigations as a tool to match scent traces

left by a perpetrator at a crime scene to the odor of a

person suspected of that crime. The protocol includes

certiﬁcation of the team involved, collecting and con-

serving scent samples at crime scenes, collecting, con-

serving and presenting suspect, and other array odors,

working procedures and reporting. Scent identiﬁcation

line-ups have evolved from simple line-ups that are

used in human scent tracking/trailing, where a dog

has to walk up to the person whose track it has been

following and through some trained behavior indic ate

the person.

▶ Odor Biometrics

Score Fusion

▶ Fusion, Score-Level

▶ Multiple Experts

Score Fusion and Decision Fusion

Score fusion is a paradigm, which calculates similarity

scores for each of the two modalities, then combines

the two scores according to a fusion formula, e.g., the

overall score is calculated as the mean of the two

modality scores. Decision fusion is a paradigm, which

makes an accept–reject decision for each of the two

modalities, then combines the two decis ions according

to a fusion rule, e.g., the unknown sample is accepted

only if both modalities yield an accept decision.

▶ Multibiometrics, Overview

Score Normalization

The score normalization techniques aim, generally, to

reduce the scores variabilities in order to facilitate the

estimation of a unique speaker-independe nt threshold

during the decision step. Most of the current normaliza-

tion techniques are based on the estimation of the impos-

tors scores distribution where the mean, μ, and the

standard deviation v, depend on the considered speaker

model and/or test utterance. These mean and standard

deviation values will then be used to normalize any

incoming score s using the normalization function

scoreNðsÞ

s  m

Two main score normalization techniques used in

speaker recognition are:

1. Znorm. The zero normalization (Znorm) method

(and its variants like Hnorm (Heck, L.P., Weintraub,

M.: Handset-dependent background models for ro-

bust text-independent speaker recognition. In:

ICASSP. (1997))) normalizes the score distribution

using the claimed speaker statistics. In other words,

the claimed speaker model is tested against a set of

impostors, resulting in an impostor similarity score

distribution which is then used to estimate the nor-

malization parameters μ and v. The main advantage

of the Znorm is that the estimation of these para-

meters can be performed during the tr aining step.

2. Tnorm. The test normalization (Tnorm)

(Auckenthaler, R., Carey, M., Lloyd-Thomas, H.:

Score normalization for text-independent speaker

veriﬁcation system s. Digital Signal Processing

10 (2000) 4254) is another score normalization

technique in which the parameters μ and v are

estimated using the test utterance. Thus, during

testing, a set of impostor models is used to calculate

impostor scores for the given test utterance. μ and v

are estimated using these scores. The Tnorm is

known to improve the performances particularly

in the region of low false alarm.

1134

Scent Identification Line-Ups

Any of a number of rules for adjusting a raw simi-

larity score in a way that takes into account factors

such as the amount of data on which its calculation was

based, or the quality of the data. One purpose of score

normalization in biometrics is to prevent the arising of

false matches simply because only a few elements (e.g.,

biometric features) were available for comparison. So

an accidental match by chance would be more like

tossing a coin only a few times to produce a perfect

run of all head. Another purpose of score normalization

is to make it possible to compare or to fuse different

types of measurements, as in multibiometrics. For ex-

ample, Z-score normalization redeﬁnes every observa-

tion in units of standard deviation from the mean,

thereby allowing incommensurable scores (like height

and weight) to become commensurable (e.g., he is 3.2

standard deviations heavier than normal but 2.3 stan-

dard deviations taller than normal). Frequently the goal

of score normalization is to map samples from different

distributions into normalized samples from a universal

distribution. For example, in iris recognition a decision is

made only after the similarity score (fractional Hamming

Distance) has been converted into a normalized score

that compensates for the number of bits that were avail-

able for comparison, thereby preventing accidental False

Matches just because of a paucity of visible iris tissue.

▶ Score Normalization Rules in Iris Recognition

▶ Session Effects on Speaker Modeling

▶ Speaker Matching

Score Normalization Rules in Iris

Recognition

JOHN DAUGMAN

Cambridge University, Cambridge, UK

Synonyms

Commensurability; Decision criterion adjustment;

Error probability non-accumulation; Normalised

Hamming Distance

Definition

All biometric recognition systems are based on similarity

metrics that enable decisions of ‘‘same’’ or ‘‘different’’ to

be made. Such metrics require normalizations in order

to make them commensurable across comparison cases

that may differ greatly in the quantity of data available, or

in the quality of the data. Is a ‘‘perfect match’’ based only

on a small amount of data better or worse than a less

perfect match based on more data? Another need for

score normalization arises when interpreting the best

match found after an exhaustive search, in terms of the

size of the database searched. The likelihood of a good

match arising just by chance between unrelated templates

must increase with the size of the search database, simply

because there are more opportunities. How should a

given ‘‘best match ’’ score be interpr eted? Addressing

these questions on a principled basis requires models

of the underlying probability distributions that describe

the likelihood of a given degree of similarity arising by

chance from unrelated sources. Likewise, if comparisons

are required over an increasing range of image orienta-

tions because of uncertainty about image tilt, the proba-

bility of a good similarity score arising just by chance

from unrelated templates again grows automatically, be-

cause there are more opportunities. In all these respects,

biometric similarity

▶ score normalization is needed,

and it plays a critical role in the avoidance of False

Matches in the publicly deployed algorithms for iris

recognition.

Introduction

Biometric recognition of a person’s identity requires

converting the observed degree of similarity between

presenting and previously enrolled features into a deci-

sion of ‘‘same’’ or ‘‘different.’’ The previously enrolled

features may not be merely a single feature set obtained

from a single asserted identity, but may be a vast number

of such feature sets belonging to an entire national

population, when identiﬁcation is performed by exhaus-

tively searching a database for a sufﬁciently good match.

The

▶ similarity metrics used for each comparison

between samples might be simple correlation statistics,

or vector projections, or listings of the features (like

ﬁngerprint minutiae coordinates and directions) that

agreed and of those that disagreed as percentages of the

total set of features extracted. For each pair of feature

sets being compared, vary ing amounts of data may be

available, and the sets mig ht need to be compared

under various transformations such as image rotations

when the orientation is uncertain. An example is seen

Score Normalization Rules in Iris Recognition

1135

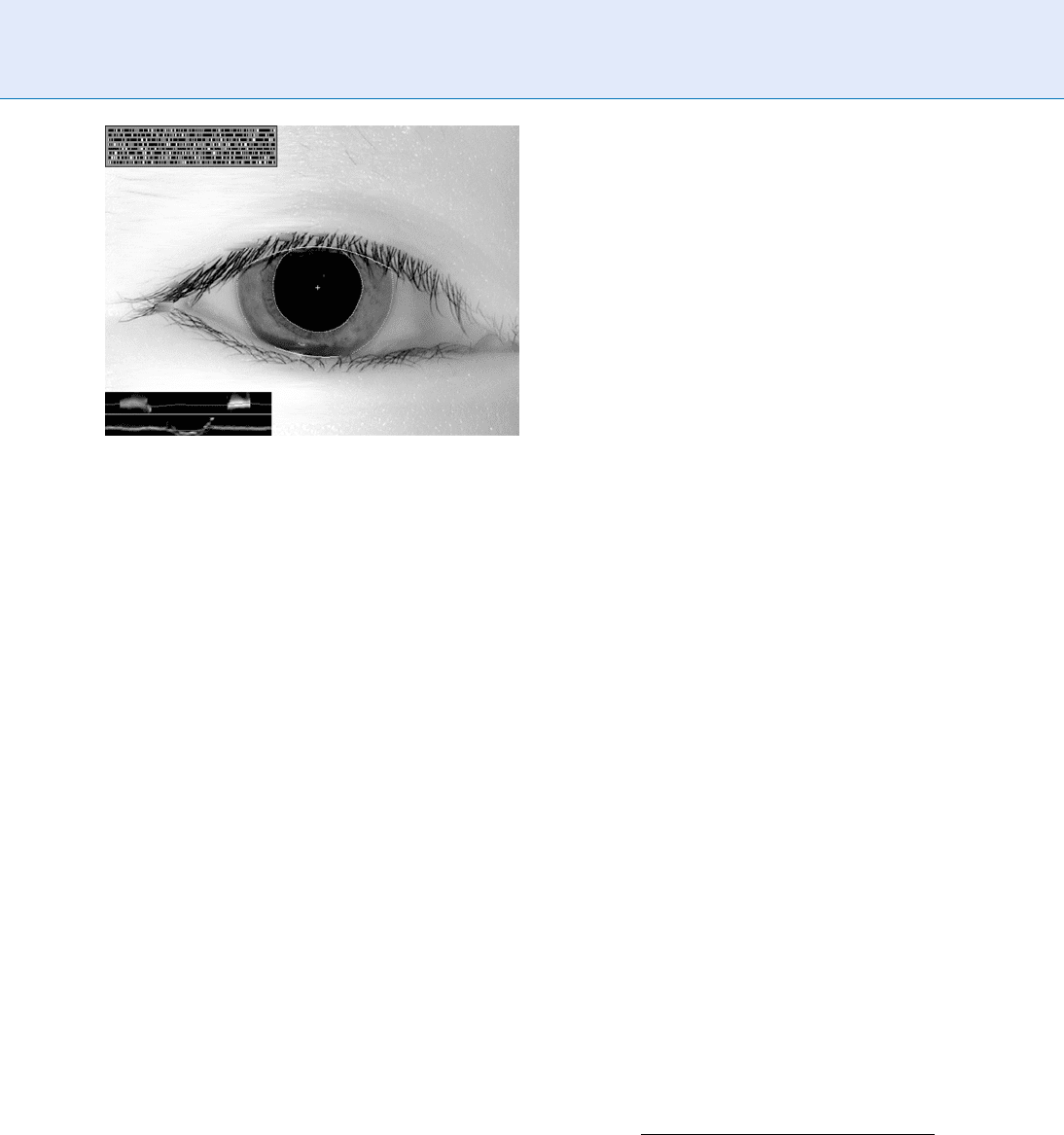
in Figure 1, in which only 56% of the annular iris area

is visible between the eyelids. Iris images may have also

been acquired with a tilted camera (not unusual for

handheld cam eras), or with the head tilted or the eye

rotated (cyclovergence) by an unknown degree, requir-

ing comparisons to be made over a range of conﬁgura-

tions for each of the possible identities, and with

varying amounts of template data being available in

each case. This article is concerned with the methods of

▶ score normalization that are used in iris recognition

to make all of those comparison cases

▶ commensura-

ble with each other, preventing False Match probability

from rising simply because there is less data available

for comparison or because there are many more can-

didates and match conﬁgurations to be considered.

Score Normalisation by the Amount

of Iris Visible

The algorithms used in all current public deployments

of iris recognition [2] work by a test of statistical

independence: A match is declared when two templates

fail the test of statistical independence; comparisons

between different eyes are statistically guaranteed to

pass that test [1]. The test of independence is based

on measuring the fraction of bits that disagreed be-

tween two templates, called

▶ IrisCodes, and so the

similarity metric is a

▶ Hamming Distance between

0 and 1. (The method by which an IrisCode is created

is described in this encyclopedia in the entry on Iris

Encoding and Recognition using Gabor Wavelets.)

If two IrisCodes were derived from different eyes,

about half of their bits should agree and half should

disagree (since any given bit is equally likely to be 1 or

0), and so a Hamming Distance close to 0.5 is expected.

If both IrisCodes were computed from the same

eye, then a much larger proportion of the bits should

agree since they are not independent, and so a

Hamming Distance much closer to 0 is expected. But

what is the effect of having varying numbers of

bits available for comparison, for example, because

of eyelid occlusion?

Eyelid boundaries are detected (as illus trated by the

spline curve graphics in Figure 1 where each lid inter-

sects the iris), and the parts of the IrisCode that are

then unavailable are marked as such by setting masking

bits. The box in the lower-left corner of Figure 1 shows

Active Contours computed to describe the pupil

boundary (lower ‘‘snake’’) and the iris outer boundary

(upper snake). As these snakes are curvature maps, a

circular boundary would be described by a snake that

was ﬂat and straight. The two thick grey regions in the

box containing the upper snake represent the limited

regions where the iris outer boundary is visible and

possesses a large radial gradient (or derivative) in

brightness. The gaps that separate the two thick grey

regions correspond to parts of the trajectory around

the iris where no such boundary is visible, because it is

occluded by eyelids. Thus the outer boundary of the

iris must be estimated (dotted curve) by two quite

limited areas on the left and right sides of the iris

where it is visible. In the coordinate system that results,

the iris regions obscured by eyelids are marked as such

by masking bits.

The logic for comparing two IrisCodes to generate a

raw Hamming Distance HD

raw

is given in Equ ation (1 ),

where the data parts of the two IrisCodes are denoted

{codeA, codeB} and the vectors of corresponding mask-

ing bits are denoted {maskA, maskB}:

raw

kðcodeA codeBÞ

maskA

maskBk

kmaskA

maskBk

ð1Þ

The symbol

signiﬁes the logical Exclusive-OR

(XOR) operator which detects disagreement between

bits;

signiﬁes logical AND whereby the masks dis-

count data bits where occlusions occurred; and the

norms kkcount the number of bits that are set in

the result. Bits may be mas ked for several reasons other

than eyelid or eyelash occlusion. They are also deeme d

Score Normalization Rules in Iris Recognition. Figure 1

Illustration of limited data being available in an iris image due

to eyelid occlusion, as detected in a segmentation process.

1136

Score Normalization Rules in Iris Recognition

unreliable if specular reﬂections are detected in the

part of the iris they encode, or if the signal-to-noise

ratio there is poor, for example, if the local texture

energy is so low that the computed wavelet coefﬁcients

fall into the lowest quartile of their distribution, or on

the basis of low entropy (informat ion density).

The num ber of bits pairings available for compari-

son between two IrisCodes, kmaskA

maskBk,is

usually almost a thousand. But if one of the irises

has (say) almost complete occlusion of its upper half

by a drooping upper eyelid, and if the other iris being

compared with it has almost complete occlusion of its

lower half, then the common area available for com-

parison may be almost nil. How can the test of statisti-

cal independence remain a valid and powerful basis for

recognition when very few bits are actually being com-

pared? It may well be that a less exact match on a larger

quantity of data is better evidence of a match than is a

perfect match on less data. An excellent analogy is a

test of whether or not a coin is ‘‘fair’’ (i.e., gives unbi-

ased outcomes when tossed): Getting a result of 100%

‘‘heads’’ in few tosses (e.g., 10 tosses) is actually much

more consistent with it being a fair coin than getting a

result of 60% / 40% after 1,000 tosses. (The latter result

is 6.3 standard deviations away from expectation,

whereas the former result is only 3.2 standard devia-

tions away from expectation; so the 60/40 result is

actually much stronger evidence against the hypothe-

sis of a fair coin, than is the result of ‘‘all heads in

10 tosses’’.) Similarly, in biometric comparisons, getting

perfect agreement between two samples that extracted

only ten features may be much weaker evidence of a

good match than a ﬁnding of 60% agreement among

a much larger number of extracted features.

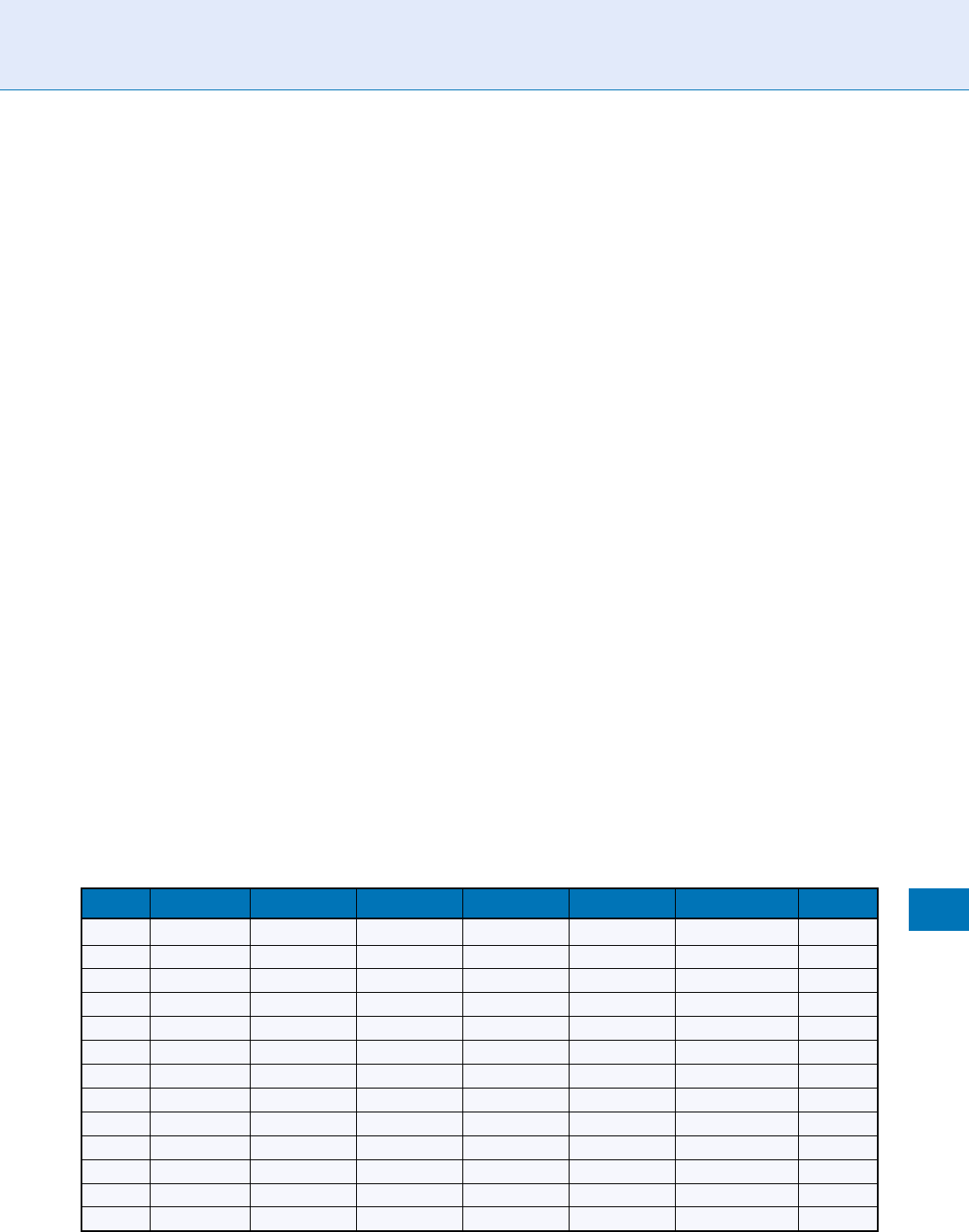
This is illustrated in Table 1 for an actual database

of 632,500 IrisCodes computed from different eyes in

a border-crossing application in the Middle East [3].

A database of this size allows 200 billion di fferent

pair comparisons to be made, yielding a distribution

of 200 billion HD

raw

similarity scores between different

eyes. These HD

raw

scores were broken down into seven

categories by the number of bits mutually available for

comparison ( i.e., unmasked) between each pair of Iris-

Codes; those bins constitute the columns of Table 1,

ranging from 400 bits to 1,000 bits being compared.

The rows in Table 1 each correspond to a particular

decision threshold being applied; for example, the ﬁrst

row is the case that a matc h is declared if HD

raw

0.260 or smaller. The cells in the Table give the ob-

served False Match Rate in this database for each

decision rule and for each range of numbers of bits

being compared when computing HD

raw

Using the ﬁndings in Table 1, it is informative to

compare performance for two decision criteria: a very

conservative criterion of HD

raw

¼0.260 (the ﬁrst row),

and a more liberal criterion HD

raw

¼ 0.285 (the sixth

row) which allows more bits to disagree (28.5%) while

still declaring a match. Now if the False Match Rates

Score Normalization Rules in Iris Recognition. Table 1 False match rate without score normalisation: dependence on

number of bits compared and criterion

Crit

400 bits 500 bits 600 bits 700 bits 800 bits 900 bits 1,000 bits

0.260 2  10

9

5  10

10

3  10

10

1  10

10

000

0.265 3  10

9

8  10

10

5  10

10

2  10

10

4  10

11

0.270 4  10

9

1  10

9

9  10

10

5  10

10

2  10

10

0.275 7  10

9

2  10

9

1  10

9

9  10

10

5  10

10

3  10

11

0.280 1  10

8

4  10

9

2  10

9

2  10

9

1  10

9

2  10

10

0.285 2  10

8

7  10

9

4  10

9

3  10

9

2  10

9

5  10

10

2  10

11

0.290 3  10

8

1  10

8

8  10

9

7  10

9

4  10

9

1  10

9

1  10

10

0.295 4  10

8

2  10

8

1  10

8

1  10

8

9  10

9

3  10

9

4  10

10

0.300 6  10

8

3  10

8

3  10

8

2  10

8

2  10

8

7  10

9

9  10

10

0.305 9  10

8

6  10

8

5  10

8

4  10

8

4  10

8

1  10

8

2  10

9

0.310 1  10

7

1  10

7

8  10

8

8  10

8

7  10

8

3  10

8

5  10

9

0.315 2  10

7

2  10

7

1  10

7

2  10

7

1  10

7

6  10

8

1  10

8

0.320 3  10

7

3  10

7

2  10

7

3  10

7

3  10

7

1  10

7

2  10

8

Score Normalization Rules in Iris Recognition

1137

are compared in the ﬁrst and last columns of these

rows, namely when only about 400 bits are available for

comparison and when about 1,000 bits are compared,

it can be seen that, in fact, the more conservative

criterion (0.260) actually produces 100 times more

False Matches using 400 bits than does the more liberal

(0.285) criterion when using 1,000 bits. Moreover, the

row corresponding to the HD

raw

¼ 0.285 decision

criterion reveals that the False Match Rate is 1,000

times greater when only 400 bits are available for

comparison than when 1,000 bits are compared.

The numerical data of Table 1 is plotted in Figure 2

as a surface, showing how the logarithm of the False

Match Rate decays as a function of both variables. The

surface plot reveals that there is a much more rapid

attenuation of False Match Rate with increase in the

number of bits available for comparison (lower-left

axis), than by reduction of the HD

raw

decision cri terion

in the range of 0.260 - 0.320 (lower-right axis). This

is to be expected, given that iris recognition works by

a test of statistical independence. The observations of

Table 1 and Figure 2 clearly demonstrate the need for

similarity scores to be normalized by the number of

bits compared when calculating them.

A natural choice for the scor e normalization rule is to

rescale all deviations from HD

raw

¼ 0.5 in proportion

to the square-root of the number of bits that were com-

pared when obtaining that score. The reason for such a

rule is that the expected standard deviation in the distri-

bution of coin-tossing outcomes (expressed as a fraction

of the n tosses having a given outcome), is s ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

pq=n

where p and q a re the respective outcome probabilities

(both nominally 0.5 in this case). Thus, decision con-

ﬁdence levels can be maintained irrespective of how

many bits n were actually compared, by mapping each

raw Hamming Distance HD

raw

into a normalized score

norm

using a re-scaling rule such as:

norm

¼ 0:5 ð0:5  HD

raw

ﬃﬃﬃﬃﬃﬃﬃ

911

ð2Þ

This normalization should transform all samples of

scores obtained when comparing different eyes into

Score Normalization Rules in Iris Recognition. Figure 2 The data of Table 1 plotted as a surface in semilogarithmic

coordinates, showing a range factor of 10,000-to-1 in the False Match Rate as the number of bits compared ranges

from 400 to 1,000. This bit count is more inﬂuential than is the HD

raw

decision criterion for unnormalised scores in the

0.260 - 0.320 range.

1138

Score Normalization Rules in Iris Recognition

samples drawn from the same ▶ binomial distribution,

whereas the raw scores HD

raw

might be samples from

many different binomial distributions having standard

deviations s dependent on the number of bits n that

were actually available for comparison. This normali-

zation maintains constant conﬁdence levels for deci-

sions using a given Hamming Distance threshold,

regardless of the value of n. The scaling parameter

911 is the typical number of bits compared

(unmasked) between two different irises.

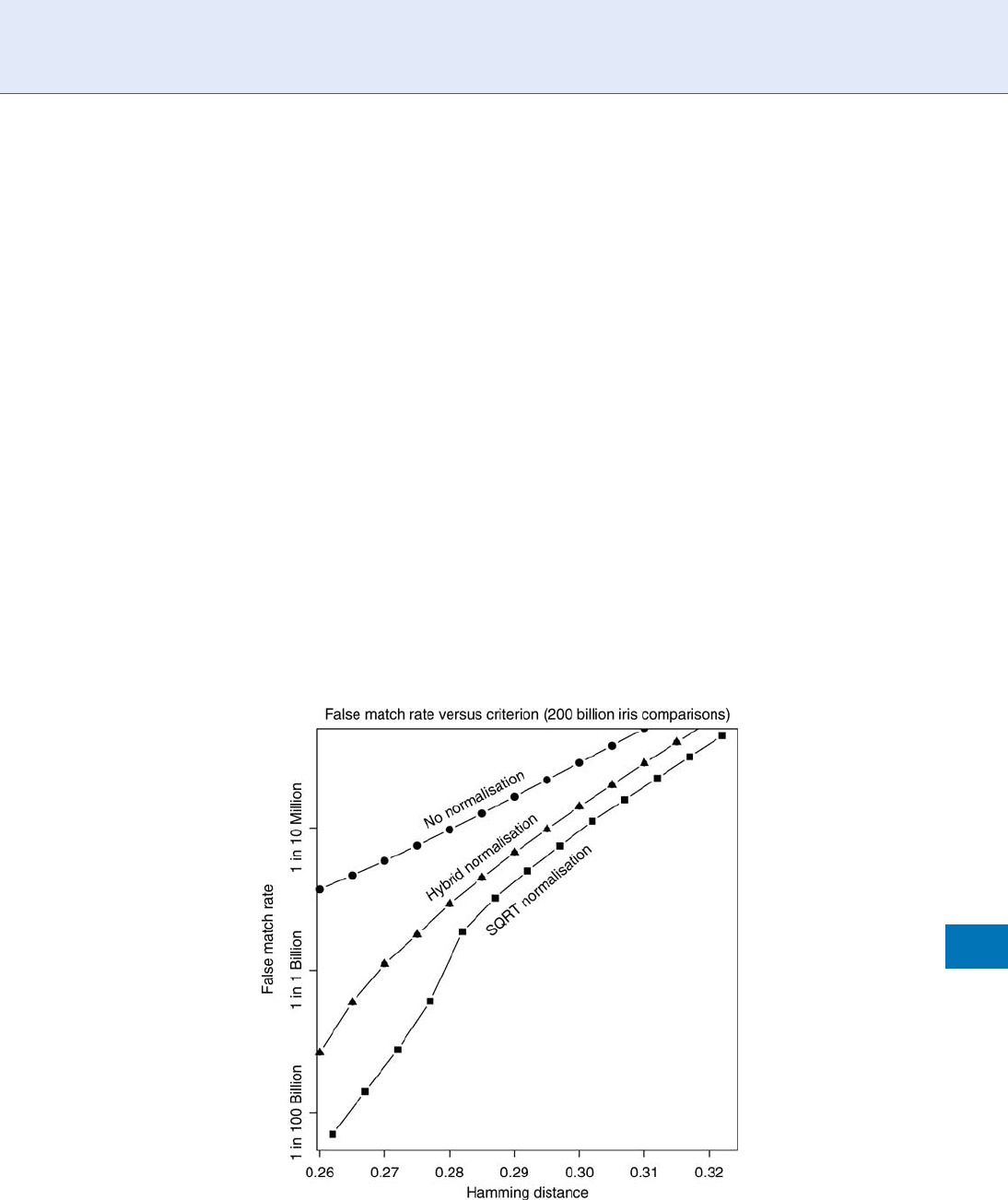
The effect of using this normalization rule

(‘‘SQRT’’) is shown in Figure 3 for the 200 billion

comparisons between different irises, plotting the ob-

served False Match Rate as a function of the new

norm

normalized decision criterion. Also shown

for comparison is the unnormalized case (upper

curve), and a ‘‘hybrid’’ normalization rule which is

a linear combination of the other two, taking into

account the number of bits compared only when in

a certain range [4]. The beneﬁt of score normalization

is profound: it is noteworthy that in this semilogarith-

mic plot, the ordinate spans a factor of 300,000 to 1.

The price paid for achieving this profound beneﬁt

in robustness against False Matches is that the match

criterion becomes more demanding when less of the

iris is visible. Table 2 shows what fraction of bits HD

raw

(column 3) is allowed to disagree while still accepting

a match, as a function of the actual number of bits that

were available for comparison (column 1) or the ap-

proximate percent of the iris that is visible (column 2).

In every case shown in this Table, the probability of

making a False Match is about 1 in a million; but it is

clear that when only a very little part of two irises can

be compared with each other, the degree of match

required by the decision rule becomes much more

demanding. Conversely, if more than 911 bits (the

typical case, corresponding to about 79% of the iris

being visible) are available for comparison, then the

decision rule becomes more lenient in terms of the

acceptable HD

raw

while still maintaining the same net

conﬁdence level.

Finally, anoth er cost of using this score norma liza-

tion rule is apparent if one operates in a region of the

ROC curve corresponding to a very nondemanding

Score Normalization Rules in Iris Recognition. Figure 3 Comparing the effects of three score normalisation rules on

False Match Rate as a function of Hamming Distance.

Score Normalization Rules in Iris Recognition

1139