Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

algorithm proposed in [14] estimates the 3D con-

ﬁguration of the head in each frame of the video.

The 3D conﬁguration consists of three translation

parameters and three orientation parameters which

correspond to the yaw, roll and pitch of the face.

The approach combines the structural advantages

of geometric modeling with the statistical beneﬁts

of a particle-ﬁlter based inference. The face is mod-

eled as the curved surface of a cylinder which is free

to translate and rotate in an unprescribed manner.

The geometric modeling takes care of pose changes

and self-occlusions while the statistical modeling

handles unexpected occlusions and illumination

variations during the course of the video. The re-

covered 3D facial pose information can be used to

perform pose normalization which makes it very

useful for the tasks of face modeling, face recogni-

tion, expression analysis, etc.

The estimation of 3D pose of a face in each frame of a

video is posed as a dynamic state estimation prob-

lem. Particle ﬁltering is used for estimating the un-

known dynamic state of a system from a collection of

noisy observations. Such an approach involves two

components: 1) a state transition model to govern

the motion of the face, and 2) an observation model

to map the input video frames to the state (3D

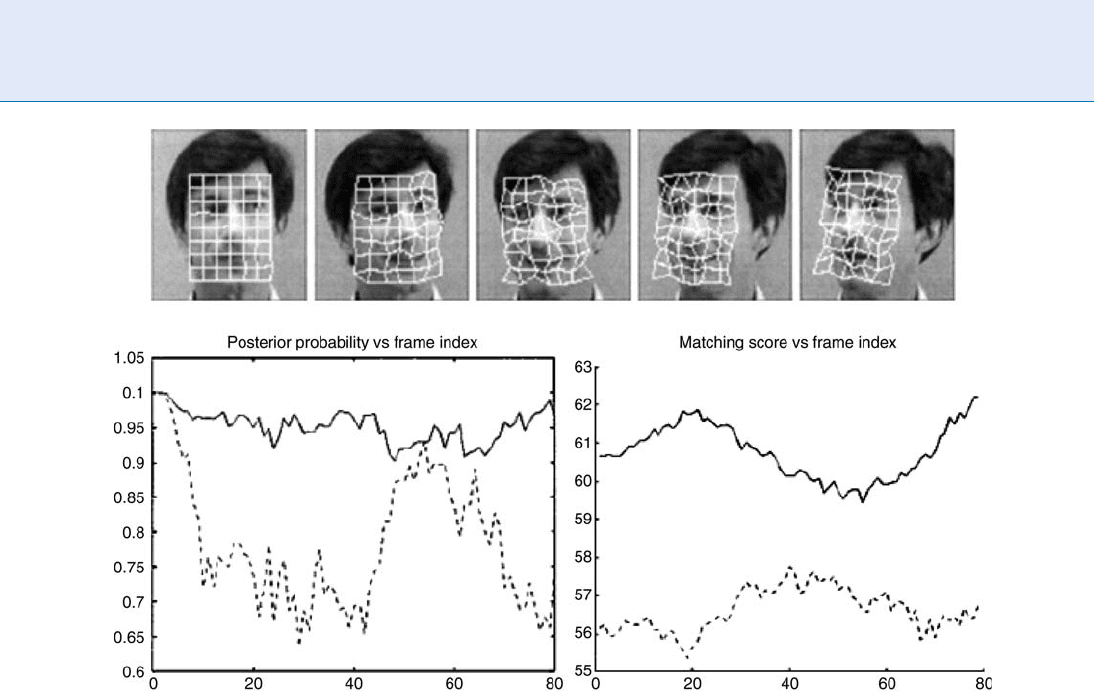
conﬁguration). Figure 3 shows the tracking results

for a few video frame. The estimated pose is shown

in the form of a overlaid cylindrical grid. The

accuracy in recovering 3D facial pose information

makes it viable to perform VFR without any need

for pose overlap between the gallery and test video.

Recognition experiments are performed on videos

with nonoverlapping poses. For each face, a texture

mapped cylindrical representation is built using the

recovered facial pose information, which is used for

matching. The approach has been tested on a small

dataset consisting of 10 subjects.

6. Shape-Illumination Manifold for VFR: In [15],

Arandjelovic and Cipolla propose a generic shape-

illumination manifold based approach to recognize

faces in videos. Assuming the intensity of each

pixel in an image to be a linear function of

the corresponding albedo, the difference in two

Face Recognition, Video-Based. Figure 2 2D feature-based approach [10]. Top: Tracking result; Bottom left:

Posterior probabilities for the true (solid) and an impostor (dashed) hypothesis; Bottom right: Matching scores for the

true (solid) and impostor hypothesis.

370

Face Recognition, Video-Based

logarithm-transformed images of the same subject

in the same pose, depends only on 3D shape of

the face and the illumination conditions in the

input images. As the pose of the subject varies,

the difference-of-log vectors describe manifold

called as shape-illumination man ifold in the corre-

sponding vector space. Assuming shape variations

across faces of different subjects to be small, a

generic shape-illumination manifold (gSIM) can

be learnt from a training corpus.

Given a test video for recognition, it is ﬁrst re-

illuminated in the illumination condition of each

gallery video. Re-illumination involves a genetic al-

gorithm (GA) based pose matching across the two

face videos. For re-illumination, each frame of the

test video is recreated using a weighted linear combi-

nation of K nearest neighbor frames of the gallery

video as di scovered by the pose matching module.

This is followed by generation of difference-of-log

vectors between each corresponding frame of the

original and re-illuminated test videos. If the gal-

lery and test video belong to the same subject, the

difference-of-log vectors depend only on shape and

illumination conditions. On the other hand, if the

two videos come from different subjects, the vec-

tors also depend on the differences in albedo maps

of the two subjects. Finally, the similarity score is

obtained by computing the likelihood of these pos-

tulated shape-illumination manifold samples

under the learnt gSIM. The approach provides

near perfect recognition rates on three different

datasets consisting of 100, 60 and 11 subjects

respectively.

7. System Identiﬁcation Approach: Aggarwal et al. [12]

pose VFR as a dynamical system identiﬁcation

problem. A moving face is modeled as a linear dyna-

mical system whose appearance changes with pose.

Each frame of the video is assumed to be the output

of the dynamical system particular to the subject.

Autoregressive and Moving Average (ARMA) model

is used to represent such a system as follows

xðt þ1Þ¼AxðtÞþnðtÞ

yðtÞ¼CxðtÞþoðtÞ

ð5Þ

Here y(t) is the noisy observation of input I(t)at

time t, such that y(t) ¼ I(t)þo(t). I(t) is the

appearance of face at time t and x

(t) is the hidden

state that characterizes the pose, expression, etc. of

Face Recognition, Video-Based. Figure 3 3D model-based approach [14]. The last column shows the pose for the

frames in the third column.

Face Recognition, Video-Based

371

the face at time t. A and C are the system matrices

characterizing the system, and n(t) is an IID reali-

zation from some unknown density q(.). Given a

sequence of video frames, Aggarwal et al. [12] use a

closed-form solution to estimate A and C. The

similarity between a gallery and a probe video is

measured using metrics based on subspace angles

obtained from the estimated system matrices. The

metrics used include Martin, gap, and Frobenius

distance, all of which give similar recognition perfor-

mance. The approach does well on the two datasets

tested in [12]. Over 90% recognition rate is achieved

(15/16 for the Li dataset [10] and 27/30 for the

UCSD/Honda dataset [9]). The performance is

quite promising given the extent of the pose and

expression variations in the video sequences.

Summary and Discussion

There is little doubt that presence of multiple video

frames allows for better generalization of person-speciﬁc

facial characteristics over what can be achieved from a

single image. In addition, VFR provides operational

advantages over traditional still image based face recog-

nition systems. Most existing VFR approaches have only

been tested on independently captured very small data-

sets. Large standard datasets are required for better eval-

uation and comparison of various approaches.

Related Entries

▶ Face Recognition Overview

▶ Face Recognition Systems

▶ Face Tracking

References

1. Zhao, W., Chellappa, R., Phillips, P.J., Rosenfeld, A.: Face recog-

nition: A literature survey. ACM Comput. Surv. 35(4), 399–458

(2003)

2. O’Toole, A.J., Roark, A., Abdi, H.: Recognizing moving faces: A

psychological and neural synthesis. Trends Cogn. Sci. 6, 261–266

(2002)

3. Hadid, A., Pietikainen, M.: An experimental investigation about

the integration of facial dynamics in video-based face recogni-

tion. Electronic Lett. Comput. Vis. Image Anal. 5(1), 1–13

(2005)

4. Ekenel, H., Pnevmatikakis, A.: Video-based face recognition

evaluation in the chil project - run 1. In: Proceedings of the

seventh International Conference on Automatic Face and Ges-

ture Recognition, pp. 85–90 (2006)

5. Gorodnichy , D. O. (Editor): Face processing in video sequences.

Image and Vis. Comput. 24(6), 551–648 (2006)

6. Grother, P., Micheals, R., Phillips, P.: Face recognition vendor

test 2002 performance metrics. In: Proceedings of fourth

International Conference on Audio and Video-Based Biometric

Person Authentication, pp. 937–945 (2003)

7. Zhou, S., Kruger, V., Chellappa, R.: Probabilistic recognition of

human faces from v ideo. Comput. Vis. Image Underst. 91(1–2),

214–245 (2003)

8. Gross, R., Shi, J.: The cmu motion of body (mobo) database.

Tech. Rep. CMU-RI-TR-01-18, Robotics Institute, Carnegie

Mellon University, Pittsburgh, PA (2001)

9. Lee, K.C., Ho, J., Yang, M.H., Kriegman, D.: Visual tracking and

recognition using probabilistic appearance manifolds. Comput.

Vis. Image Underst. 99(3), 303–331 (2005)

10. Li, B., Chellappa, R.: Face veriﬁcation through tracking facial

features. J. Opt. Soc. Am. A 18(12), 2969–2981 (2001)

11. Liu, X., Chen, T.: Video-based face recognition using adaptive

hidden markov models. In: Proceedings of International

Conference on Computer Vision and Pattern Recognition,

pp. 340–345 (2003)

12. Aggarwal, G., Roy-Chowdhury, A.K., Chellappa, R.: A system

identiﬁcation approach for video-based face recognition.

In: Proceedings of International Conference on Pattern Recog-

nition, pp. 175–178 (2004)

13. Liu, J.S.: Monte carlo strategies in scientiﬁc computing. Springer

(2002)

14. Aggarwal, G., Veeraraghavan, A., Chellappa, R.: 3d facial pose

tracking in uncalibrated videos. In: Proceedings of International

Conference on Pattern Recognition and Machine Intelligence,

pp. 515–520 (2005)

15. Arandjelovic, O., Cipolla, R.: Face recognition for video

using the general shape-illumination manifold. In: Proceed-

ings of European Conference on Computer Vision, pp. 27–40

(2006)

Face Reconstruction

▶ Forensic Evidence of Face

Face Registration

▶ Face Alignment

372

Face Reconstruction

Face Sample Quality

KUI JIA

,SHAOGANG GONG

Shenzhen Institute of Advanced Integration

Technology, CAS/CUHK, Shenzhen, People’s Republic

of China

Queen Mary, University of London, London, UK

Synonyms

Face sample standardization; Face sample utility

Definition

Face is a human biometric attribute that can be used to

establish the identity of a person. A face-based biomet-

ric system operates by capturing probe face samples

and comparing them against gallery face templates.

The intrinsic characteristic of captured face samples

determine their effecti veness for face authentication.

Face sample quality is a measurement of these intrinsic

characteristics. Face sample quality has signiﬁcant

impact on the performance of a face-based biometric

system. Recognizing face samples of poor quality is a

challenging problem. A number of factors can contrib-

ute toward degradation in face sample quality. They

include, but not limited to, illumination variation,

pose variation, facial expression change, face

occlusion, low resolution, and high sensing noise.

Introduction

A typical face-based biometric system operates by

capturing face data (images or videos), and comparing

the obtained face data against face templates of differ-

ent individuals in a gallery set. While face templates in

the gallery set are normally captured under constrained

imaging conditions (e.g., from frontal view, at a short

distance from the camera, and under consistent illumi-

nation), it is unrealistic to assume controlled acquisi-

tion of probe face data. Face data captured under

uncontrollable environment usually contains many

kinds of defects caused by poor illumination, improper

face positioning, and imperfect camera sensors [1].

For instance, when face data is captured in a natural

outdoor environment, inconsistent illumination is

typically cast on human faces resulting in uneven,

extremely strong or weak lightings. Face rotation can

also cause signiﬁcant appearance variations, and at the

extreme, face can be self occluded (Fig . 1). When dis-

tances between human faces and cameras increase,

captured face data will be at low resolution, in low

contrast, and likely to contain high imaging noise. In

some instances people may wear sunglasses, have vary-

ing facial expression, and be with heavy makeup. All

of these factors contribute toward potential degrada-

tion in the quality of captured face samples, resulting

in disparities to those of face templates stored in the

gallery set.

Face sample quality has signiﬁcant impact on

the performance of face-based biometric systems.

Face Sample Quality. Figure 1. Face samples of illumination and pose variations from AR and UMIST databases.

Face Sample Quality

373

Assessing the quality of face samples before applying

them in any biometric system may help improve the

authentication accuracy. For example, an intruder may

wear sunglasses intending to disguise himself, quality

assessment of intruder’s face samples can give an alert

to such a situation. Quantitative measures on the

quality of face samples can also be integrated into

biometric systems to increase or decrease relevant

thresholds. In a people enrollment stage, such qu anti-

tative measures of quality also help procure gallery face

templates of good quality. Many approaches assess face

sample quality using general image properties in clud-

ing contrast, sharpness, and illumination intensity [2].

However, these properties cannot properly measure

face sample degradation caused by inconsistent illumi-

nation, face rotation, or large face-camera distance.

There are a few recent works assessing face sample

quality by considering such kinds of degradation. For

example in [1], facial-symmetry-based methods are

used to measure facial asymmetries caused by non-

frontal lighting and improper facial pose.

When only poor quality face data can be acquired

at the authentication stage, face recognition becomes

signiﬁcantly more challenging because of: (1) Illumi-

nation variation to which the performance of most

existing face recognition algorithms and systems is

highly sensitive. It has been shown both experimentally

[3] and theoretically [4] that face image differences

resulting from illumination variation are more signi-

ﬁcant than either inherent face differences between

different individuals, or those from varying face poses

[5]. State of the art approaches addressing this prob-

lem include heuristic methods, reﬂectance-model

methods, and 3D-model-based methods [6]. Although

performance improvement is achieved, none of these

methods are truly illumination invariant. (2) Pose

variation which causes face recognition accuracy to

decrease signiﬁcantly, especially when large pose varia-

tions between gallery and probe faces are present. The

difﬁculties would fur ther increase if only an unknown

single pose is available for each probe face. In such a

situation, an extra independent training set, different

from the galley set and containing multiple face images

of different individuals under varying poses, will be

helpful. Three-dimensional face model or statistical

relational learning between different poses can be

employed to generate virtual face poses. By generating

virtual poses, one can either normalize probe faces of

varying poses to a predeﬁned pose, e.g., frontal, or

expand the gallery to cover large pose variations.

(3) Low resolution face data will be acquired when

face-camera distances increase, which is rather typical

in surveillance imagery. The performance of existing

face recognition systems decreases signiﬁcantly when

the resolution of captured face data is reduced below a

certain level. This is because the missing high-resolu-

tion details in facial appearances and image features

make facial analysis and recognition ineffective,

either by human operators or by automated systems.

It is therefore useful to generate hi gh-resolution

face images from low-resolution ones. This tech-

nique is know n as face hallucination [7] or face

▶ super-resolution.

Assessment of Face Sample Quality

The performance of face authentication depends

heavily on face sample quality. Thus the signiﬁcance

of face sample quality assessment and standardization

grows as more practical face-based biometric systems

are required. Quality assessment of probe face samples

can either reject or accept a probe to improve later

face veriﬁcation or identiﬁcation accuracy. Quantita-

tive assessment of face sample qu ality can also be used

to assign weights in a biometric fusion scheme.

ISO/IEC WD 2979 4-1 [8] considers that biometric

sample quality can be deﬁned by character (inherent

features), ﬁdelity (accuracy of features), or utility (pre-

dicted biometrics performance). Many efforts have

been made on biometric sample quality assessment

for ﬁngerprint, iris, or face data. Most of those on

face data are based on general image properties includ-

ing contrast, sharpness, and illumination intensity [2].

However, the face sample degradation that severely

affects face authentication accuracy is from uncontrol-

lable imaging conditions that cause illumination varia-

tions, head pose changes, and/or very low-resolution

facial appear ances. There are a few attempts made on

assessing face sample quality caused by these kinds of

degradation.

In [9], two different strategies for face sample qual-

ity assessment are considered: one is for illumination

variation and pose change, another is for facial expres-

sion change. In the ﬁrst strategy, speciﬁc measures are

deﬁned to correlate with levels of different t ypes of face

sample degrad ation. A polynomial function is then

utilized based on each measure for predicting the

374

Face Sample Quality

performance of a ▶ Eigenface technique on a given face

sample. Quality goodness is assessed by selecting a

suitable threshold. Since the measurement of facial

expression intensity is difﬁcult, in the second strategy,

a given face sample is classiﬁed into good or poor

quality based on its coarse similarity to neutral facial

expression. Then the training procedure for each class

is achieved by dividing the training set into two sub-

sets, based on whether the samples are recognizable by

the Eigenface technique. Then these two subsets are

described by Gaussian mixture models (GMMs). In [1],

facial-symmetry-based quality scores are used to assess

facial asymmetr ies caused by non-frontal lighting and

improper facial pose. In particular, local binary pattern

(LBP) histogram features are applied to measure the

lighting and pose asymmetries. Moreover, the inter-eye

distance is also used to estimate the quality score for

whether a face is at a proper distance from the camera.

Recognizing Face Samples of

Poor Quality

In general, face recognition under varying illumination

is difﬁcult. Although existing efforts to address this

challenge have not led to a fully sati sfactory solution

for illumination invariant face recognition, some

performance improvements have been achieved. They

can be broadly categorized into: heuristic methods, re-

ﬂectance-model methods, and 3D-model-based meth-

ods [6]. A typical heuristic method applies subspace

learning, e.g., principal component analysis (PCA),

using training face samples. By discarding a few most

signiﬁcant, e.g., the ﬁrst three, principal components,

variations due to lighting can be reduced. Reﬂectance-

model methods employ a Lambertian reﬂectance

model with a varying albedo ﬁeld, under the assump-

tion of no attached and cast shadows. The main disad-

vantage of this approach is the lackof generalization from

known objects to unknown objects [10]. For 3D-face

model-based approaches, more stringent assumptions

are often made and it is also computationally less reli-

able. For example in [11], it is assumed that the 3D face

geometry lies in a linear space spanned by the 3D geom-

etry of training faces and it uses a constant albedo ﬁeld.

Mor eov er, 3D model-based methods require complex

ﬁtting algorithms and high-resolution face images.

There are also attempts to address the problem

of face recognition across varying facial poses.

In real-world applications, one may have multiple

face samples of varying poses in training and gallery

sets (since they can be acquired ofﬂine), while each

captured probe face can only be at an unknown single

pose. Three-dimensional model-based methods [12]

or statistical learning-based methods can be used to

generate virtual face poses [13], by which either probe

faces can be normalized to a predeﬁned pose, e.g. frontal

view, or gallery faces can be expanded to cover large pose

variations. For example in [12], a 3D morphable model

is used. The speciﬁc 3D face is recovered by simulta-

neously optimizing the shape, texture, and mapping

parameters through an analysis-by-synthesis strategy.

The disadvantage of 3D model-based methods is slow

speed for real-world applications. Learning-based meth-

ods try to learn the relations between different facial

poses and how to estimate a virtual pose in 2D domain,

e.g., the view-based active appearance model (AAM)

[14]. This method depends heavily on the accuracy of

face alignment, which unfortunately introduces anoth-

er open problem in practice.

When the resolution of captured face data fall s

below a cer tain level, exis ting face recognition system s

will be signiﬁcantly affected. Face super-resolut-

ion techniques have been proposed to address this

challenge. Reconstruction-based approaches require

multiple, accurately aligned low-resolution face sam-

ples to obtain a high-resolution face image. Their

magniﬁcation factors of image resolution are however

limited [7]. Alternatively, learning-based face super-

resolution approaches model high-resolution training

faces and learn face-speciﬁc prior knowledge from

them. They use the learned model prior to constrain

the super-resolution process. A super-resolution factor

as high as 4  4 can be achieved [7]. The face super-

resolution process can also be integrated with face

recognition. For example in [15], face image super-

resolution is transferred from pixel domain to a lower

dimensional eigenface space. Then the obtained high-

resolution face features can be directly used in face

recognition. Simultaneous face super-resolution and

recognition in

▶ tensor space have also been intro-

duced [16]. Given one low-resolution face input of

single modali ty, the proposed method can integrate

and realize the tasks of face super-resolution and rec-

ognition across different facial modalities including

varying facial expression, pose, or illumination.

This has been further generalized to unify automatic

alignment with super-resolution [17].

Face Sample Quality

375

Summary

Many face-based biometric systems have been dep-

loyed in applications ranging from national border

control to bu ilding door access, which normally solve

the sample quality problem at the initial face acquisi-

tion stage. Given ongoing progress on standardization

of face sample quality and technical advancement in

authenticating face samples of poor quality, the avail-

ability of more reliable and convenient face authenti-

cation systems is only a matter of time.

Related Entries

▶ Biometric Sample Quality

▶ Face Pose Analysis

▶ Face Recognition

References

1. Gao, X.F., Li, S.Z., Liu, R., Zhang, P.R.: Standardization of

face image sample quality. In: Proceedings of Second Interna-

tional Conference on Biometrics (ICB), pp. 242–251. Seoul,

Korea (2007)

2. Brauckmann, M., Werner, M.: Technical report. In: Proceedings

of NIST Biometric Quality Workshop. (2006)

3. Adini, Y., Moses, Y., Ullman, S.: Face recognition: the problem of

compensating for changes in illumination direction. IEEE Trans.

Pattern Anal. Mach. Intell. 19(7), 721–732 (1997)

4. Zhao, W., Chellappa, R.: Robust Face Recognition Using Sym-

metric Shape-from-Shading. Technical Report, Center for Auto-

mation Research, University of Maryland (1999)

5. Tarr, M.J., Bulthoff, H.H.: Image-based object recognition in

man, monkey and machine. Cognition 67, 1–20 (1998)

6. Zhao, W., Chellappa, R., Phillips, P.J., Rosenfeld, A.: Face recog-

nition: a literature survey. ACM Comput. Surv. 35(4), 399–458

(2003)

7. Baker, S., Kanade, T.: Limits on super-resolution and how to

break them. IEEE Trans. Pattern Anal. Mach. Intell. 24(9),

1167–1183 (2002)

8. ISO/IEC JTC 1/SC 37 N 1477: Biometric Sample Quality

Standard – Part 1: Framework (2006)

9. Abdel-Mottaleb, M., Mahoor, M.H.: Application notes -

algorithms for assessing the quality of facial images. IEEE Com-

put. Intell. Mag. 2(2), 10–17 (2007)

10. Baker, S., Kanade, T.: Appearance characterization of linear

lambertian objects, generalized photometric stereo, and illumi-

nation-invariant face recognition. IEEE Trans. Pattern Anal.

Mach. Intell. 29(2), 230–245 (2007)

11. Atick, J., Grifﬁn, P., Redlich, A.: Statistical approach to shape

from shading: reconstrunction of 3-dimensional face surfaces

from single 2-dimentional images. Neural Comput. 8 (2),

1321–1340 (1996)

12. Blanz, V., Vetter, T.: Face recognition based on ﬁtting a 3-D

morphable model. IEEE Trans. Pattern Anal. Mach. Intell.

25(9), 1063–1074 (2003)

13. Li, Y., Gong, S., Liddell, H.: Constructing facial identity surfaces

for recognition. Int. J. Comput. Vision 53(1), 71–92 (2003)

14. Cootes, T.F., Walker, K., Taylor, C.J.: View-based active appear-

ance models. In: Proceedings of Fourth International Con-

ference on Automatic Face and Gesture Recognition (FG),

pp. 227–232. Grenoble, France (2000)

15. Gunturk, B.K., Batur, A.U., Altunbasak, Y., Hayes, M.H.,

Mersereau, R.M.: Eigenface-Domain Super-Resolution for Face

Recognition. IEEE Transactions on Image Processing, 12(5),

597–606 (2003)

16. Jia, K., Gong, S.: Multi-modal tensor face for simultaneous

super-resolution and recognition. In: Proceedings of Tenth In-

ternational Conference on Computer Vision (ICCV), pp. 1683–

1690. Beijing, China 2 (2005)

17. Jia, K., Gong, S.: Generalised face super-resolution. IEEE Trans-

actions on Image Processing, 17(6), 873–886(2008).

Face Sample Standardization

▶ Face Sample Quality

Face Sample Synthesis

SAMI ROMDHANI,JASENKO ZIVANOV

Computer Science Department, University of Basel,

Basel, Switzerland

Synonyms

Face image synthesis; Rendering; Image formation

process

Definition

Face Sample Synthesis denotes the process of generat-

ing the image of a human face by a computer program.

The input of this process is a set of parameters that

376

Face Sample Standardization

describes (1) the position from which the face is vie-

wed, (2) the illumination environment around the face,

(3) the identity of the person, and (4) the expression of

the person. Other parameters may also be used such as

the age of the person, parameters describing the make-

up, etc. The output is an image of a human face.

Introduction

Face Sample Synthesis denotes the process of generating

theimageofahumanfacebyacomputerprogram.

Optimally, this image should be realistic and virtually

indistinguishable from a photography of a live scene.

Addi tionally, the computer prog ram should be gene r-

ic: able to synthesize the face of any individual, viewed

from any pose and illuminated by any arbitrarily

complex environment. The objective o f this ar tic le is

to review the techniques used to reach this goal. It may

also be desirable to g enerate faces w ith different

expressions, different attributes such as makeup st yle

or facial hair. One might also want to render image

sequences with realistic facial motion. However, it is

outside the scope of this article to address the methods

enabling such synthesizes.

A photograph of a face is a projection onto an

image plane of a 3D objec t. The intensity of a pixel

of this photograph directly depends on the amount of

light that is reﬂected from the object point imaged at

the pixel location. Thus, this article ﬁrst reviews 3D

to 2D projections (the ﬁnite projective camera model)

and illumination modeling (the Lambertian and

Phong light reﬂection models usually used in face

recognition systems). Then, the basics of identity mod-

eling are summarized. At the end of the article, the

reader will have an overview of the process required

to synthesize a face image from any individual, viewed

from any angle, and illuminated from any direction.

Research on computer-based face recognition dates

back from the 1970s. In those times, most popular

methods (e.g ., [1]) were based on distances and angles

between landmark points (such as eyes and mouth

corners, nostril, chin top, etc.). Then, in the beginning

of the 1990s, the appearance-based methods came in

and quickly attracted most of the attention [2]. Con-

trasting with the former landmark points methods,

these techniques use the entire face area for recogni-

tion. They are based on a prior generative model capa-

ble of synthesizing a face image given a small number

of parameters. Analysis is performed by estimating the

parameters, denoted by

y, which synthesize a face

image that is as similar as possible to the input

image. Hence, these methods are called Analysis by

Synthesis. This is usually done using a sum of square

error functions:

y¼ arg min

i;input

 I

i;model

ðyÞk

; ð1Þ

where the index i represent pixel i and the sum runs

over all pixels of the face area. The formation of the

model image, I

model

(y), is the topic of this article.

Initially, the models used a 2D representation of the

face structure [2], however, in order to account for

pose and illumination variation, it is accepted that

3D models provide more accurate results [3, 4].

Hence, this article rev iews the process of generati ng a

face image from a 3D model.

Four ingredients are necessary to synthesize a face

from a 3D representation [5]: The face surface of the

individual to be imaged must be sampled across a

series of points resulting in a list of 3D vertices.

Obtaining a surface from a list of vertices is achieved

by a triangle list that connects triplets of vertices. The

triangle list deﬁnes the topology of the face. It is used,

among other things, to compute surface normals and

the visibility of a surface points using (for instance) a

‘‘Z-buffer’’ visibility test.

The third constituent is the color of the face. It can

be represented by an RGB color for a dense set of

surface points. These surface points are called ‘‘texels.’’

If the texels are the same points as the vertices, then the

color model is called ‘‘per vertex color.’’ Alternatively, a

much denser texel sampling can be used and the texels

are arranged in a ‘‘texture map.’’ In order to synthesize

unconstrained illumination image s, the texels must be

free of any illumination effect and code the ‘‘albedo’’ of

a point. The albedo is deﬁned as the diffuse color

reﬂected by a surface point. Finally, the last ingredient

is a reﬂectio n model that relates the camera direction

and the intensity of light reﬂected by a surface point, to

the intensity, the direction, and the wavelength of lig ht

reaching the point.

Finite Projective Camera Model

This section brieﬂy describes how a 3D object is

imaged on a 2D image.

Face Sample Synthesis

377

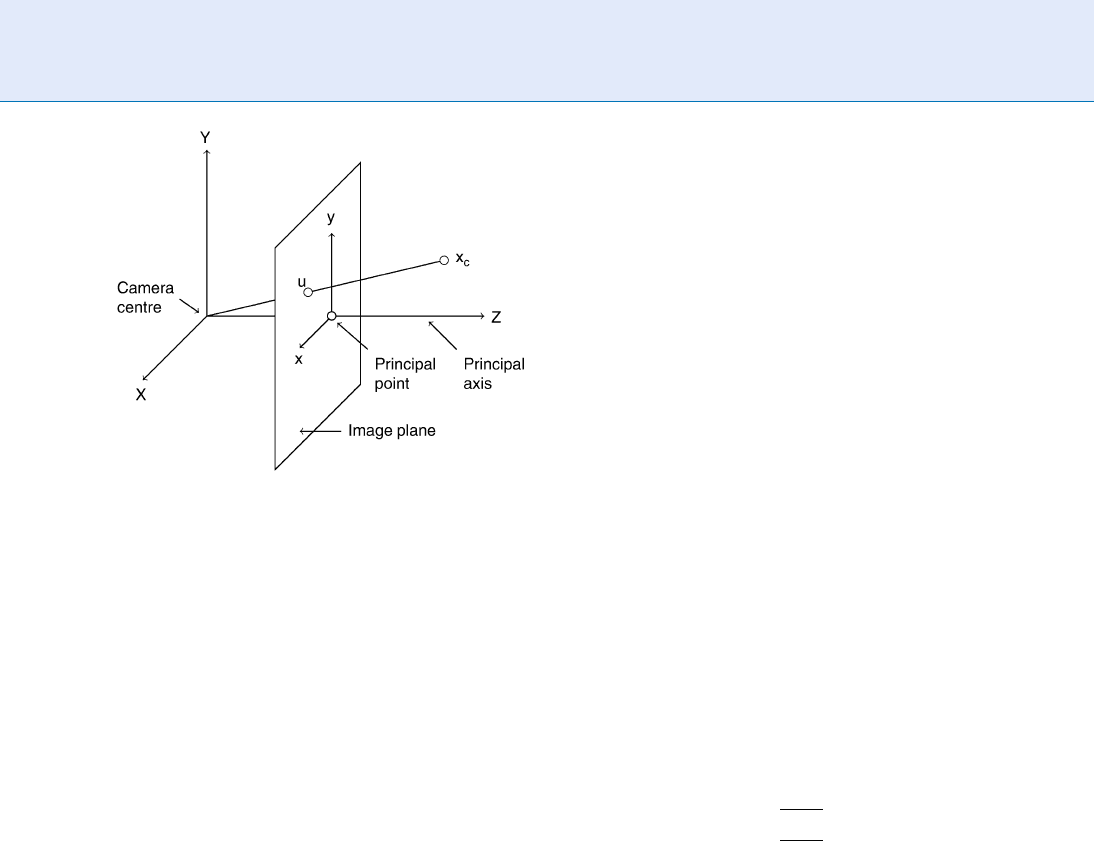
In Computer Vision and Computer Graphics,

a ﬁnite projective camera model is usually chosen.

This camera follows a central projection of points in

space onto a plane. For now, lets assume that the

camera is at the origin of an Euclidean coordinate

system and that it is pointing down the Z-axis.

In that sy stem, a 3D point, x

¼( X

)

is projected

onto a 2D point, u, in the image frame according to

the following equation, in which the focal length,

denoted by f, is the distance between the camera

center and the principal point: u¼(fX

∕Z

,fY

∕Z

This equation assumes that the origin of the image

plane coordinate system is at the principal point.

In general, it might not be and, denoting the coordi-

nates of the principal point by (p

), the mapping

becomes:

u ¼ðfX

þ p

; fY

þ p

Þ: ð2Þ

In a face image synthesis, the point x

is one vertex

of the 3D shape of a face in camera coordinate frame.It

is easier to represent the ensemble of vertices of the face

in an object coordinate frame. The origin of this frame is

attached to the object, a typical choice is to locate it at

the center of mass of the face. The 3D coordinate of the

camera center in the object frame is denoted by c.

Additionally, the object coordinate frame is gener-

ally not aligned with the camera coordinate frame, i.e.,

the face is not always frontal. The rotation between the

face and the camera is denoted by the 3 3 matrix R .It

can be represented by a product of rotations along the

coordinate axes of the object frame:

10 0

0 cosðaÞ sinðaÞ

0 sinðaÞ cosðaÞ

;

cosðbÞ 0 sinðbÞ

010

sinðbÞ 0 cosðbÞ

;

cosðgÞ sinðgÞ 0

sinðgÞ cosðgÞ 0

001

; R ¼ R

ð3Þ

The relation between the object and camera frames is

then: x

¼ R(x  c). It is often convenient not tomake

the camera center explicit and to introduce t¼Rc.In

this case, the relation is simply:

¼ Rx þ t: ð4Þ

As a result, projecting a point x in object coordinate

frame onto the image plane is summarized by the

following expression, in which R

denotes the row

number i of the matrix R.

¼ f

xþt

þ p

¼ f

xþt

þ p

(

ð5Þ

Estimating the parameters of a ﬁnite projective

camera model requires then the estimation of nine

parameters: f, a, b, g, t

, t

, p

. Note that in

this explanation some subtle parameters that have only

a minor effect on the synthesis and on the analysis by

synthesis results are neglected: Some CCD cameras

do not have square pixels (two additional parameters)

and the skew parameter that is zero for most normal

cameras [6].

Lighting Model

The previous section showed where, in the image, to draw

a surface point from its 3D coor dinates. No w the question

is: What pixel value to draw on this point? The pixel value

is the intensity of the light reﬂected by the surface point,

whichiscomputedusingalightingmodel.Muchofthe

realism of a rendering depends on the

▶ lighting model.

378

Face Sample Synthesis

This model, in turn, depends on three factors: The

number and type of light sources, the reﬂectance func-

tion, and the method used to compute surface normals.

Light modeling is still undergoing considerable research

efforts in the computer graphics community (the main

challenge being to make photo-realistic rendering algo-

rithms computationally efﬁcient). In this article, the

fundamental notions are only brieﬂy introduced.

If lig ht is emitted from direction



l with intensity l,

then the quantity of light received by an inﬁnitesimally

small surface patch around surface point x is h



li l,

where



, is the normal of the surface patch at the point

x and h,i is the scalar product (if it is positive and null

otherwise). If the surface point projects onto pixel i of

the image, yields

i;model

¼ r



lÞh



;



lil  S



; ð6Þ

where r

() denotes the reﬂectance function at point x

and



v, the viewing direction (deﬁned as the direction

from the point to the camera center). S



denotes the

cast shadow binary variable: If there is another object

or if some part of the face is between point x and the

point at inﬁnity in direction



l, then the light is sha-

dowed at the point, and S



is zero, other wise it is

equal to one. Cast shadows are usually computed by

a shadow map [7].

Light Source

The simplest and most computationally efﬁcient is to

use one directed light source at inﬁnity and one ambient

light source. The light reﬂected by a surface point from

an ambient light source does not depend on the local

surface around the point, it only depends on the albedo

of the point. In real world, however, a perfectly ambient

light never exists and it rarely happens that a point is

illuminated only by a single light source. Indeed, light

emanating from a light source might bounce off a wall,

for instance, and then reach the object point. Hence, in

real world, light comes from all directions. An environ-

ment map [8] is usually used to model this effect.

It codes the intensity of light reaching an object for a

dense sampling of directions. It is acquired by photo-

graphing a mirrored sphere [9]. Due to the additive

nature of light, rendering with several light sources

(as is the case for environment maps) is performed

by summing (or integrating) over the light sources:

i;model



Þh



;



il

 S



: ð7Þ

The following image is an environment map ac-

quired at the Ufﬁzi Gallery in Florence, Italy. Each pixel

of this photograph is attached to a direction and rep-

resent a light source. This environment map is used to

illuminate Panel d of Fig.1.

Reflectance Function

In (6), the four-dimensional reﬂectance function

(



l) is called the Bidirectional Reflectance Distribu-

tion Function (BRDF). It also depends on the wave-

length of the incoming light (usually represented by its

RGB color). The BRDF describes the properties of the

material at point x.

The simplest model of reﬂectance function is cer-

tainly the Lambertian model for which the function

is equal to a constant (the albedo at point x). This

means that incident light is scattered equally in all

directions, which only happens for perfectly diffuse

objects (totally matte, without shininess). For human

face, this is the case only when the skin is covered by a

very ﬁne layer of powder. An example of rendering

with a Lambertian reﬂectance is displayed on Fig.1a.

Specular reﬂection takes place when light is reﬂected

at a point without absorption by the material. F or per-

fectly specular material, such as mirrors, light is reﬂected

in only one direction (the reﬂectance function is a Dirac

function): when the viewing angle is equal to the angle

Face Sample Synthesis

379