Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

conditions have varied over the years. But perhaps the

main legacy of this development of what is also called

multiresolution analysis was the uniﬁcation of the local

and the spectral perspectives into a single framework:

as the name ‘‘wavelet’’ implies, the terms of analysis

became simultaneously local, yet frequency-speciﬁc.

One important practical manifestation of these theo-

retical developments is found in JPEG-2000 compres-

sive image encoding, which is based on a class of

wavelets developed by Ingrid Daubechies [4].

But as early as 1946 a class of wavelet-like elem en-

tar y functions named logons (from the Greek word for

‘‘order’’) had been proposed by the Hungarian physi-

cist Denis Gabor [5], who also invented holography

and won the Nobel Prize in 1971. Although these

functions lack some of the stricter requirements on

wavelets, they satisfy more lax deﬁnitions and they

have certain advantages including being expressible in

closed analytic form (i.e., they can be deﬁned in terms

of classical functions). They take the form of complex

exponentials (i.e., Fourier components) multiplied

by Gaussian envelopes, which localize them and specify

their scale. Whether or not their parameters are con-

strained to maintain self-similar proﬁles at all scales

(a conﬁguration not anticipated by Gabor), these

wavelets can form a ‘‘frame’’ and can be used as a

basis for complete expansions: any signal or image

can be constructed as a linear combination, or super-

position, of such wavelets. This is illustrated in the

lower two panels of Fig. 1: those two reconstructions

were synthesized entirely from a discrete dyadic set

of self-similar complex Gabor wavelets using only six

frequencies and six orientations, as shown in Fig. 2.

The library of self-similar Gabor wavelets whose

real and imaginary parts are portrayed pictorially in

Fig. 2 differ from each other in frequency by steps of

one octave (successively doubling in frequency, while

their Gaussian widths are successively halved). They

are deﬁned in each of six orientations. Being complex

functions, their parts have two phases: cosine (even-

symmetric) and sine (odd-symmetric). This library

emulates the architecture found in the brain’s visual

cortex, whose neural receptive ﬁelds are structured for

sequential orientation selectivity [6], size or spatial

frequency selectivity with roughly one octave half-

bandwidth and receptive ﬁeld proﬁles [7] whose

excitatory/inhibitory inputs resemble the structures

seen in Fig. 2 with quadrature (90

∘

) phase-tuned

elements arranged in sine/cosine pairs [8]. Taken

together, these empirical neurophysiological observa-

tions support the ‘‘2D Gabor mode l’’ [9] of image

representation in the brain’s visual cortex, but practical

engineering implementation of it is complicated by the

fact that these wavelets constitute a nonorthogonal set.

Their lack of mutual independence (their nonzero

inner product) has the consequence that the coefﬁ-

cients needed for image expansion or reconstruction

are not the same as the coefﬁcients obtained simply by

projecting the image onto the wavelets; they cannot be

obtained merely by ﬁltering or convolution with the

image. A solution for ﬁnding correct expansion coefﬁ-

cients so that the wavelets can be used as a complete

image basis is a ‘‘relaxation network’’ [10]. This meth-

od is how the synthetic iris images in the lower panels

of Fig. 1 were constructed, using only the di screte set

of wavelets seen in Fig. 2 having six frequencies, one

octave apart (the lowest frequency wavelet being omit-

ted as it ﬁlls the entire image) and six orientations. It is

Iris Encoding and Recognition using Gabor Wavelets.

Figure 2 Visual library of real and imaginary parts of

the 2D Gabor wavelets, defined in six discrete

orientations and in six discrete frequencies that differ

from each other in one octave steps (i.e., by successive

factors of two). The lowest of the six frequencies is not

included here as it fills the entire image. This discrete set of

wavelets is the set that was used to synthesize the two iris

images as shown in the lower two panels of Fig. 1,

reconstructing the original natural images seen in the

upper two panels.

790

Iris Encoding and Recognition using Gabor Wavelets

clear that the superposition, or linear combination, of

these discrete wavelets using appropriately computed

coefﬁcients converges faithfully to the original images

in the upper panels, up to the resolution determined by

the highest frequency wavelet used. Thus the discrete

ensemble of computed wavelet coefﬁcients, which may

be called a complete discrete 2D

▶ Gabor Transform

[10], capture all the information in the original images

and, more importantly, constitute an extremely useful

representation of it.

Gabor Wavelets and the Uncertainty

Principle

The evident richness of natural iris textures, as

illustrated in Fig. 1, invites description that is speciﬁc

both in spectral terms (the frequencies and orienta-

tions of in terwoven undulations), and in spatially

localized terms. Yet these two goals are in mutual

conﬂict, because of a fundamental Uncertainty Princi-

ple [5, 9] that makes the resolution of either type of

information possi ble only at the expense of resolution

for the other. The Uncertainty Principle is a funda-

mental law of mathematics, not simply an empirical

problem; it can be derived as a general relationship

constraining functions and their Fourier transforms.

One particular instantiation of it is the familiar

Heisenberg Uncertainty Principle in quantum physics:

the position and the momentum of a particle cannot

be known with simultaneously unlimited accuracy,

given that its momentum is interpretable as wave-

length and therefore has spectral speciﬁcity. The

abstract form of the Uncertainty Principle asserts a

lower bound on the product of the ‘‘effective width’’

of any function and that of its Fourier transform. The

functions that uniquely achieve this lower bound, and

therefore achieve maximal speciﬁcity or localizability

in both domains at once, are the (complex-valued)

Gabor wavelets [5].

Deﬁned in two dimensions with (x,y) interpretable

as image coordinates, these wavelets have the following

parameterized functional form [9]:

f ðx; yÞ¼e

ðxx

þðyy

½

ðxx

Þþv

ðyy

½

;

ð1Þ

where (x

) specify the wavelet’s center position in

the image, (a,b) specify its effective width and length,

and (u

) specify its modulation, which has spatial

frequency o

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ v

and orientation y

¼arctan

∕u

). (A further degree-of-freedom not included

above is the relative orientation of the ellipt ic Gaussian

envelope, which creates cross-terms in xy.) The 2D

Fourier transform F(u,v ) of a 2D Gabor wavelet has

exactly the same functional form, with parameters just

interchanged or inverted:

Fðu; vÞ¼e

ðuu

þðvv

½

ix

ðuu

Þþy

ðvv

½

ð2Þ

Thus Gabor wavelets are self-Fourier, since f(x,y) has

the same form as F(u,v). The modulation parameters

) in the image domain play the role of location

parameters in the Fourier domain, specifying a wave-

let’s peak frequency and orientation sensitivity if used

as a ﬁlter. The width and length parameters a and b

which set the effective size of the Gaussian envelopes

play reciprocal roles in the two domains: the larger a

wavelet is in one domain, the smaller it is in the other,

as dictated by the Uncertainty Principle. Finally, some

further interesting properties of Gabor wavelets be-

sides their completeness (ability to be an expansion

basis for other functions, like the iris images in Fig. 1)

and their self-Fourier property, are that as a family of

functions they are closed under multiplication and

under convolution: the product of any two Gabor

wavelets is just another Gabor wavelet; and indeed

the convolution of any two Gabor wavelets is also just

another Gabor wavelet. For our present purp oses, their

most useful property besides their optimal joint speci-

ﬁcity in both spatial and spectral terms is their utility

for analyzing image structure, including deﬁning the

phase of any element of an image since the wavelets are

complex-valued, and the utilit y of such descriptions

for pattern recognition.

Gabor Wavelets and the Calculus

It is clear from the functional form deﬁning f (x,y)

above that Gabor wavelets reduce to pure Fourier

components when the Gaussian space constants (a,b)

become large. Then the use of these functions for

image analysis becomes equivalent to Fourier analysis:

the Fourier transform is just a special case of a Gabor

transform. At the other extreme, in the limit that (a,b)

become small , the functions reduce to delta functions,

Iris Encoding and Recognition using Gabor Wavelets

791

simply sampling particular points in the image. Thus,

the Gaussian scale parameter essentially creates a con-

tinuum that bridges the dichotomy between local

(point sampling) and global (Fourier) analysis, em-

bracing those classical approaches as the end points of

the continuum. At points between those two extremes,

the wavelets enable a kind of local spectral analysis to

be performed, extracting Fourier-like information

(e.g., phase and frequency descriptions) but in a local

region-speciﬁc fashion.

When Gabor wavelets are used as ﬁlters to convolve

with a signal, their effect depends of course on the

values chosen for their parameters. If the size of the

Gaussian is large compared w ith the modulation wave-

length, allowing several cycles of oscillation before

attenuation, then the complex wavelet becomes a nar-

rowband ﬁlter that allows a well-deﬁned phase to be

assigned to each point in the output signal. Speciﬁcally,

the phase assigned to a point is the arctangent of the

ratio of the imaginary part to the real part of

the complex-valued result of the convolution with the

signal at that point. But for smaller Gaus sian space

constants that allow only one or two cycles of oscilla-

tion before attenuation, the wavelets behave instead

like approximate ﬁrst- and second-order differential

operators.

Figure 3 illustrates (for the one-dimensional case)

how convolution with such wavelets approximates tak-

ing the ﬁrst or second derivative of a signal. The real

and imaginary parts of a Gabor wavelet having such a

parameterisation are plotted in the ﬁrst and third

panels. The second panel plots the second ﬁnite differ-

ence kernel, which is the discrete ﬁlter that should be

convolved with a discrete signal (a signal deﬁned only

on a discrete domain, such as the integers or a regular

sampling lattice) in order to obtain the discrete ap-

proximation to a second derivative. There is an obvi-

ous resemblance between the continuous and the

discrete functions plotted in the ﬁrst and second

panels. Likewise, the fourth panel plots the discrete

approximation for a ﬁrst-derivative operator, called

the ﬁrst ﬁnite difference kernel, which resembles the

imaginary part of a Gabor wavelet (third panel). The

deﬁnitions of the ﬁnite difference approximations

provided on the left in this Figure correspond to

Isaac Newton’s [11] formulae for estimating the ﬁrst

or second derivatives (“Fluxions’’) of functions by

combining adjacent sample values on regular unit

sampling intervals, using weighting coefﬁcients such

as [1, +2, 1]. In summary, the information extrac-

ted by convolving a signal with Gabor wavelets having

parameterizations as indicated in Fig. 3 is closely

related to the information obtained when the machin-

ery of the Calculus is used to extract the ﬁrst and

second derivatives of a function. These properties con-

tribute to the richness of the repertoire deployed by

using complex-valued Gabor wavelets for image cod-

ing and analysis.

Gabor Wavelets for Iris Recognition

The goals of pattern recognition are, of course, rather

different from those of image encoding or analysis

perse. However, when designing a pattern recognition

system, it is nice to know that the image representation

chosen is in principle complete, meaning that all in-

formation is available in the encoding as demonstrated

by reconstructibility (Fig. 1), and also that interesting

operations are implementable in the encoding such as

extracting phase structure or derivatives (Fig. 3).

Iris Encoding and Recognition using Gabor Wavelets.

Figure 3 Analyzing and encoding signals or data using

Gabor wavelets with narrow Gaussians corresponds to

estimating a signal’s first- and second-derivatives (or finite

differences). These are approximated by convolving the

signal with the imaginary and real parts, respectively, of a

complex Gabor wavelet as shown in the right column.

Such operations correspond simply to weighting adjacent

samples algebraically (left column) with weights such as

[1, +1] or [1, +2, 1] as noted in 1671 by Isaac Newton

[11] in his theory of Fluxions.

792

Iris Encoding and Recognition using Gabor Wavelets

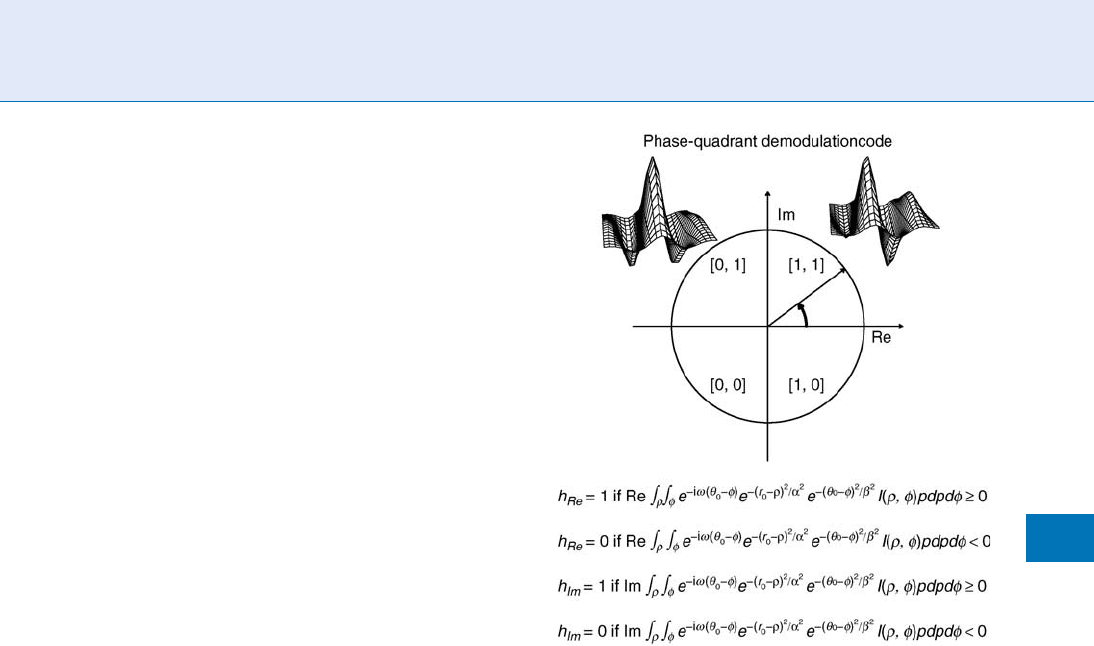
Interest in phase structure and in the zero-crossings

of bandpass signals was invigorated three decades ago

by some surprising proofs and critical demonstrati ons

of complete signal reconstructibility from either ty pe

of information alone [12]. Phase and zero-crossings

information are closely related: when a signal has been

bandpass-ﬁltered (so that it has zero mean) and digi-

tized, then the most-signiﬁcant-bit (MSB) of its sam-

ples corresponds to the most fundamental phase

information, the sign bit; and of course this bit tracks

the signal’s zero-crossings. In order to conjoin such

signal descriptions with representations on which

decisions about pattern identity can be made, we

need a kind of conceptual signal-to-symbol converter.

One very efﬁcient way to bridge this gap is to deploy

the multi-scale Gabor wavelets as

▶ logico-linear

operators, constructing bit streams from the quantiza-

tion of the phas e information that the wavelets extract.

In the case of iris recognition, such a bit stream is

called an

▶ IrisCode, and it allows identiﬁcation

decisions to be based on a simple test of statistical

independence [1].

Figure 4 illustrates how the paired real and imagi-

nary parts of 2D Gabor wavelets can be used to con-

struct a phase demodulation code. Local patches of the

image are projected onto both parts of the complex-

valued w avelets, and each pair of resulting inner pro-

ducts constitute the real and imaginary parts of a

complex number. Such a number has a phase and

a modulus corresponding to its polar components in

the complex plane, as portrayed in the phasor diagram.

If one chose to resolve phase angles to an accuracy of

only four quadrants as shown, then one would be

extracting just two bits of phase information per wave-

let. How ﬁnely should phase be quantized when

encoded? How spatially ﬁne in size (how high in fre-

quency) should the discrete set of wavelets get? Both of

these questions relate to the number of degrees-of-

freedom one wishes to encode, and to how accurately

one can realign encodings of subsequent images of the

same iris in correspondence with an earlier image of it.

Sharpening the ﬁnest scale of detail extracted makes

the code for a given iris more detailed and more

unique (thereby further decreasing the likelihood of

False Matches), but by increasing the amount of min-

ute detail that must be matched, such a strategy also

increases the odds of failures-to-match (False non-

Matches) due to uncertainties or inadequacy in regis-

tration and alignment.

Code design issues also involve other aspects of the

Gabor wavelet parameterization, including their band-

width, which is determined by the effective number of

oscillatory cycles contained within the Gaussian enve-

lope before attenuation. More cycles cause narrower

bandwidth: ﬁlters that are more sharply tuned. Related

to this issue is the presence of a DC term (nonzero

area or volume in the integral) in the real part of a

Gabor wavelet if its bandwidth is broad (has only

few cycles within the Gaussian); this is undesirable

because it introduces code bit dependence on the

overall brightness of the image, which ought to be

irrelevant. However, the DC term can be nulled to

zero when determining the sampling rate of the dis-

crete taps which discretize the continuous wavelet, or

alternatively by tiny adjustments in the discrete taps

Iris Encoding and Recognition using Gabor Wavelets.

Figure 4 Constructing an IrisCode from phase analysis of

iris texture. The two surfaces plotted are the real and

imaginary parts of one 2D Gabor wavelet. Projecting a local

area of the iris image onto these functions and integrating

their products produces a complex number, whose real and

imaginary parts specify a phasor in the complex plane as

illustrated. Phase angle can be quantized at a chosen

resolution accuracy (in this diagram, two bits for four

quadrants) to create a phase-based IrisCode. The four

equations give the projection integrals that specify the bits.

Iris Encoding and Recognition using Gabor Wavelets

793

themselves. A more fundamental issue when specifying

code design is the phase coherence introduced by the

wavelets if their bandw idth is narrow, because this

reduces the randomness among the bits extracted by

the code.

This issue is illustrated in Fig. 5, whose panels show

the relationship between the real a nd imaginary parts

of an IrisCode. Any bit of an IrisCode has equal a priori

probabilities of being set or clear (ignoring the detec-

tion and masking of eyelids, eyelashes, reﬂections, or

Iris Encoding and Recognition using Gabor Wavelets. Figure 5 Correlations between the real and imaginary parts of

IrisCodes constructed from narrowband wavelets containing several cycles. Although orthogonality of the two

quadrature pair components of a wavelet ensures that corresponding real and imaginary bit pairs are independent

(upper panel), they show strong correlation when the two bit streams are simply shifted relative to each other by an

amount corresponding to p∕2 in wavelet phase (lower panel). This means that little additional entropy is gained by using

both quadrature components if the wavelets selected are narrowband.

794

Iris Encoding and Recognition using Gabor Wavelets

other corruptions), and one should expect the real and

imaginary bit pairs to be independent because of the

orthogonality of the corresponding parts of the Gabor

wavelets. Therefore, as with any sequence of ‘‘tosses’’

from two independent and fair ‘‘coins,’’ one should

expect a 50%-5 0% level of agreement between the

bits just by chance. For quadrature IrisCode bit pairs,

this is conﬁrmed in the upper panel of Fig. 5, showing

the frequency with which different

▶ Hamming Dis-

tances (proportion of disagreeing bits) were observed

between the corresponding real and imaginary parts of

545 IrisCodes, computed over all pairs of {Re, Im}

corresponding bits. With a mean Hamming Distance

of 0.501  0.011, the expected ﬁnding of independence

between such equiprobable bits is clearly observed.

However, because the wavelets used to compute these

IrisCodes had relatively narrow bandwidths, a strong

degree of phase coherence is present in their outputs.

The consequence of such phase coherence is that the

real and imaginary parts be come hi ghly correlated

under a shift.

The lower panel of Fig. 5 plots a histogram of

Hamming Distances observed between the real and

imaginary bit streams after one stream has been shifted

by p ∕2 relative to the other. Now we see that these bit

streams are far from independent. Instead, with an

average probability of 0.912, they are simply comple -

ments of each other. The cause of this effect is clear

from the fact that narrowband wavelets (encompassing

many cycles) are almost equivalent to each other, or

negatively so, when shifted by  p ∕2. In the case

illustrated by Fig. 5, the negative correlation is so

strong that there is little justiﬁcation for using both

sets of bits if they are computed using relatively nar-

rowband wavelets; almost no additional entropy (or

information) is gained. Of course, this does not apply

to wavelets having broader bandwidth, when, as noted

in Fig. 3, the relationship is more like that between the

ﬁrst and second derivatives. In that case, if one were

forced to choose one over the other, the second deriv-

ative (corresponding to the real part of a Gabor wave-

let) would be the better choice, because the ﬁrst

derivative is sensitive to grad ients of illumination, as

may often occur in iris recognition systems using off-

axis illumination.

In the version of this algorithm that is currently

used in all public deployments of iris recognition

worldwide, the wavelet parameters were chosen to

optimize operation in identiﬁcation mode, which

requires exhaustive search through enrolled databases

without succumbing to False Matches despite the large

numbers of possibilities. The beneﬁt of operating

in this mode is that users need not assert their iden-

tities, as would be required by operation in veriﬁca tion

mode in which only a one-to-one comparison is done

against a single identity asserted by, for example, a

token or card. But successful operation in identiﬁca -

tion mode requires that the distribution of similarity

scores obtained when different irises are compared

must be conﬁned by rapidly attenuating tails, since

that distribution is effectively being sampled a large

number N times when searching a database where

the number N of stored IrisCodes might correspond

to the size of a nation’s population. The larger the

number of samples N, the greater the likelihood of

ﬁnding a sample far out along the tail and thus a

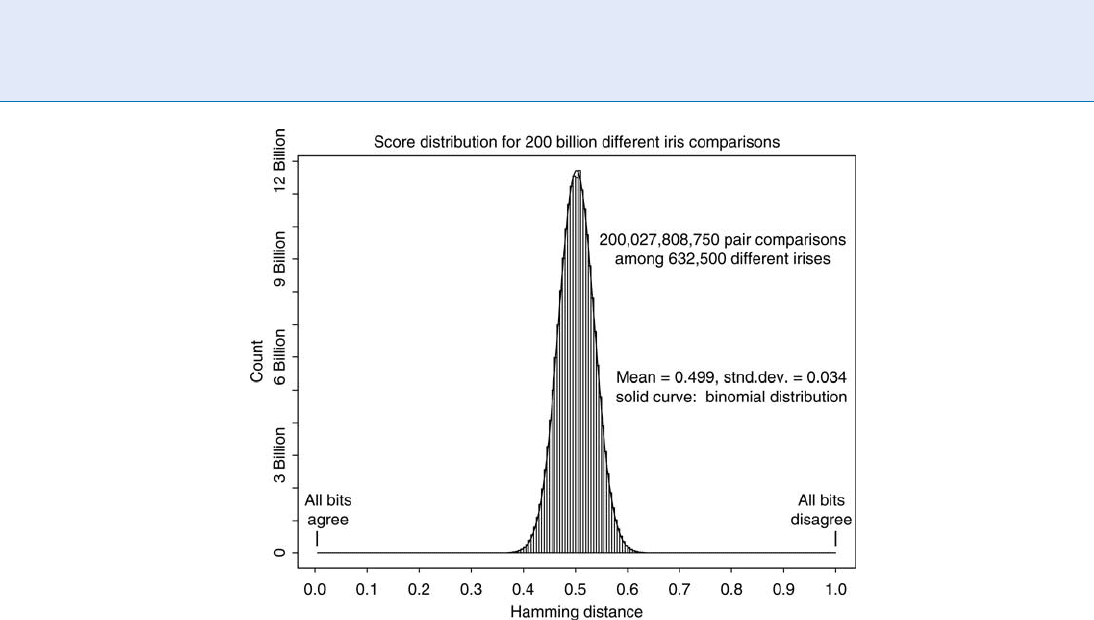
possible False Match. Figure 6 shows the result of

200 billion iris cross-comparisons obtained from one

such national border-crossing deployment at all air,

land, and seaports of entry into the United Arab Emi-

rates. Since comparisons between different persons

never generate Hamming Distance (dissimilarity frac-

tion) scores smaller than about 0.25, at least among

these 200 billion such comparisons, we see that suc-

cessful recognition using this biometric requires only

that different images of a given iris are of sufﬁcient

quality that no more than about 25% of their com-

puted IrisCode bits disagree. Under reasonable image

acquisition conditions, this is easily achieved.

Gabor Wavelets in Other Biometrics

A powerful advantage of the Gabor wavelet approach

to iris encoding and recognition is its great speed. The

complete execution time for all aspects of the image

processing, starting with a raw image, including the

localisation of the iris, detection of all boundaries

including eyelids and their exclusion, detection and

removal of eyelashes and other noise, normalization

in a dimensionless coordinate system, and demodula-

tion and compilation of the IrisCode with its masking

bits, is less than 30 ms on a 3 GHz processor. This

speed means that more than 30 complete image frames

can be fully processed per second, and so the process

can operate at the same rate as the video frame rate

itself. Of the 30 ms consumed per image frame, the vast

majority of processing time is spent on localization,

segmentation, and normali zation operations; less than

1 ms is consumed by demodulation with the Gabor

Iris Encoding and Recognition using Gabor Wavelets

795

wavelets and creation of the IrisCode. Once an Iris-

Code has been computed, the simplicity of the com-

parison process and decision algorithm allows

databases to be searched at the speed of about 1 million

IrisCodes/second per 3 GHz processor.

Since these execution speeds for image processing

and for matching are very favorable compared to those

of other biometrics, efforts have been made to adapt

these methods for the other modalities as well. Notable

among these are face [13], ﬁngerprint [14], and palm-

print [15] recognition. Besides the speed advantage, and

the design beneﬁts of formulating a biometric recogni-

tion task as a test of statistical independence on the

outputs of logico-linear operators, the mathematical

merits of Gabor wavelets as reviewed in this chapter

also contribute fundamentally to the success of this

framework for image coding and pattern recognition.

Related Entries

▶ Active Contours in Iris Recognition

▶ Iris-on-the-Move™

References

1. Daugman, J.G.: High conﬁdence visual recognition of persons by

a test of statistical independence. IEEE Trans. Pattern Anal.

Mach. Intell. 15, 1148–1161 (1993)

2. Daugman, J.G.: How iris recognition works. IEEE Trans. Circuits

Syst. Video Technol. 14, 21–30 (2004)

3. Meyer, Y.: Principe d’incertitude, bases hilbertiennes et algebres

d’operateurs. Bourbaki Seminar 662 (1985)

4. Daubechies, Y.: Orthonormal bases of compactly supported

wavelets. Comm. Pure Appl. Math. 41(7), 909–996 (1988)

5. Gabor, D.: Theory of communication. J. Inst. Electr. Eng. 93,

429–457 (1946)

6. Hubel, D.G., Wiesel, T.N.: Sequence regularity and geometry of

orientation columns in the monkey striate cortex. J. Comp.

Neurol. 158, 267–293 (1974)

7. Jones, J.P., Palmer, L.A.: An evaluation of the 2D Gabor ﬁlter

model of simple receptive ﬁelds in cat striate cortex. J. Neuro-

physiol. 58, 1233–1258 (1987)

8. Pollen, D.A., Ronner, S.F.: Phase relationships between

adjacent simple cells in the visual cortex. Science 212,

1409–1411 (1981)

9. Daugman, J.G.: Uncertainty relation for resolution in

space, spatial frequency, and orientation optimised by two-

dimensional visual cortical ﬁlters. J. Opt. Soc. Am. A 2,

1160–1169 (1985)

Iris Encoding and Recognition using Gabor Wavelets. Figure 6 Distribution of Hamming Distance scores (fraction of

disagreeing bits) obtained in 200 billion cross-comparisons among 632,500 different iris patterns enrolled in the

United Arab Emirates border-crossing deployment. The rapid attenuation of the left tail means that False Matches are

avoided even in exhaustive searches through national databases, provided that the decision policy allows no more than

about 25% of the bits to disagree (HD < 0.25) when declaring a match.

796

Iris Encoding and Recognition using Gabor Wavelets

10. Daugman, J.G.: Complete discrete 2D Gabor transforms by

neural networks for image analysis and compression. IEEE

Trans. Acoust. Speech Signal Process. 36, 1169–1179 (1988)

11. Newton, I.: Method of ﬂuxions. Manuscript in Trinity College

Library, University of Cambridge (1671)

12. Oppenheim, A.V., Lim, J.S.: The importance of phase in signals.

Proc. IEEE 69, 529–541 (1981)

13. Wiskott, L., Fellous, J.M., Kuiger, N., von der Malsburg, C.: Face

recognition by elastic bunch graph matching. IEEE Trans. Pat-

tern Anal. Mach. Intell. 19, 775–779 (1997)

14. Jain, A.K., Prabhakar, S., Hong, L., Pankanti, S.: Filterbank-

based ﬁngerprint matching. IEEE Trans. Image Process. 9,

846–859 (2000)

15. Kong, A.W.K.: Palmprint Iientiﬁcation based on generalization

of irisCode. Ph.D. thesis, University of Waterloo, ON, Canada

(2007)

Iris Image Capture Device

▶ Iris Acquisition Device

▶ Iris Device

Iris Image Data Interchange

Formats, Standardization

JAMES L. CAMBIER

Crossmatch Technologies, RCA Blvd, FL, USA

Synonyms

Iris interchange format standards; Iris data interchange

standards

Definition

Iris recognition is a biometric technology that uses the

unique, stable, and repeatable texture patterns ob-

served within the iris of the human eye, the colored

annular ring that surrounds the pupil. Iris recognition

systems typically consist of specialized cameras and

software that processes images of the eye to extract

and encode iris features in a template, and match the

presented iris templates to those in a database to iden-

tify the indiv idual. Applications include controlled

access to buildings, border security, trusted traveler

programs, and authentication of emergency aid, enti-

tlement, and citizen beneﬁt recipients. Iris image inter-

change standards have been developed to facilitate

the exchange of iris image data among diverse cameras,

processing algorithms, and biometric databases. Exist-

ing standards include ANSI INCITS 379 Iris Image

Interchange Format and ISO/IEC 19794-6 Information

technolog y: Biometric data interchange formats –

Part 6: Iris image data.

Introduction

The human ▶ iris is a colored annular ring that sur-

rounds the

▶ pupil, a variable aperture that admits

light to form an image on the

▶ retina, the light-sen si-

tive surface in the back of the eye. The iris is a mu scular

structure that contains a variety of texture features,

including pits, furrows, and radial striations (Fig. 1).

The rich and unique texture of the iris has long been

recognized, and a number of biometric systems based

on the iris have been described [1–4]. Particular algo-

rithmic approaches to the extraction, encoding, and

matching of iris texture features have also been pub-

lished [5–8].

With the advent of multiple vendors of iris cameras

and systems, and various algorithmic approaches to

Iris Image Data Interchange Formats, Standardization.

Figure 1 Iris image.

Iris Image Data Interchange Formats, Standardization

797

iris-based recognition, it became clear that the devel-

opment of data interchange standards for iris images

would (1) facilitate the exchange of iris images

among multiple vendors, applications, and algorithms,

(2) enable the compilation of iris image databases for

comparative testing and evaluation of multiple algo-

rithms, and (3) support the evolutionary development

of new iris algorithms by preserving existing enroll-

ment databases in the form of reusable images.

The development of iris standards has been a col-

laborative effort of a number of biometric vendors,

government agencies, and academic institutions, and

has resulted in both a US standard, ANSI INCITS 379

Iris Image Interchange Format [9], and an interna-

tional standard, ISO/IEC 19794-6 Information tech-

nology: Biometric data interchange formats – Part 6:

Iris image data [10]. The ANSI standard was developed

ﬁrst and became the basis for the international stan-

dard; as a result the two are virtually identical.

The iris standards support two different data for-

mats, a

▶ rectilinear format in which the iris image

is represented in standard Cartesian (x  y) coordi-

nates, and a

▶ polar format, in which the (approxi-

mately) circular iris is represented in polar (r  y)

coordinates. The rectilinear format provides the high-

est interoperability, while the polar format retains

only the area of speciﬁc interest, the iris, and thus

provides a more compact representation. The stan-

dard allows a number of different image intensity

representations (color, monochrome, etc.), compres-

sion schemes, and geometric orientations. Finally, an

appendix to the standard contains a set of recommenda-

tions for iris image capture, addr essing quality metrics,

resolution, illumination, distortion, noise, orientation,

and other properties.

Data Formats

The iris image record is a nested structure that contains

several headers and one or more images (Fig. 2). The

overall structure consists of a CBEFF header [11], the

Biometric Data Block (BDB), and a Security Block

(SB). The CBEFF header contains information about

image quality, the origin of the BDB format used, and

information about the type of biometric contained in

the data record. The BDB contains an Iris Record

Header, one or two Feature Headers, and one or

more images, each preceded by an Image Header. The

Record Header contains information and parameters

specifying the format of all of the images in the record,

such as geometric format (rectilinear or polar), orien-

tation, dimensions, number of intensity levels, number

of intensit y bands (i.e., monochrome, color, etc.), and

compression methods. The Feature Header indicates

which eye was imaged (left or right), if know n, and the

number of images recorded for that eye. Finally the

Image Header contains an image sequence number,

image quality value, size of the image data, and infor-

mation about the rotational position of the iris, if

known.

The rectilinear image format is a conventional

image composed of rows and columns where each

entry corresponds to one pixel (picture element) pro-

duced by the image sensor. If the image contains mul-

tiple color bands, such as red-green-blue, each pixel is

recorded as three sequential values.

An image in polar format is produced by proces-

sing the rectilinear image to ﬁnd the iris center, pupil

boundary, and outer iris boundary or

▶ limbus. The

portion of the image containing the iris is then sam-

pled along radial lines emanating from the iris center

and extending from the pupil boundary to the iris

boundary at particular angles. The result is an image

in polar coordinates. It is stored as a matrix in which

each column corresponds to one angular orientation

y and each row corresponds to a particular radial

distance r. Interoperability of polar images may be

limited by the accuracy and consistency with which

Iris Image Data Interchange Formats, Standardization.

Figure 2 Iris image data record.

798

Iris Image Data Interchange Formats, Standardization

the pupil and iris boundaries are determined. Their

advantage is very compact iris data representation,

since no image information within the pupil or outside

the iris is included.

Image Properties

The properties recorded for rectilinear and polar

images differ to some extent. The properties are as

follows, with these differences noted:

Image orientation – the images may be recorded in

‘‘canonical’’ form, in which the top of the eye is at the

top (ﬁrst row) of the image and, for a right eye, the

nasal side of the eye (that closest to the nose) is on

the right side of the image. Alter natively, the image

may be ﬂipped vertically or horizontally. For polar

images the orientation refers to the rectilinear image

used to produce the polar image.

Scan type – the images may have been collected

using progressive scanning, in which each row is cap-

tured in sequence, or interlaced scanning, in which all

odd rows are captured followed by all even rows. Note

that in the latter case the image is still stored in strict

row sequence.

Data format – the images may be uncompressed (or

‘‘raw’’) or compressed; they may be color or mono-

chrome, and if compressed the applicable compression

standard is referenced.

Image size – the image dimensions are recorded as

width and height, recognizing that for polar format the

width corresponds to angular samples and the height

to ra dial samples. The number of bits allocated to each

intensity value is also recorded.

Rotation angle – relative rotation between enroll-

ment and recognition images must be either corrected

or accommodated in the match process by searching

over a range of rotations [5, 7] or using templates

based on rotation-invariant features [3 ]. Some cameras

are capable of approximating the

▶ rotation angle by

capturing both eyes simultaneously and calculating the

angle of the interpupillary line with a horizontal refer-

ence. This angle information may be recorded.

Camera information – space is allocated in the

image properties to record a unique identiﬁer for the

camera and the date and time of capture.

Occlusion marking – local areas of the iris may be

occluded by reﬂections, eyelids, or eyelashes and

therefore, should not be used to generate template

information. The standard includes ﬁelds for recording

whether occlusions have been detected, and if so how

they are marked in the image data (usually as a re-

served intensity value).

Image Quality

The iris standard allows the originator of an iris image

to indicate the quality of the image on a scale from 1 to

100. The interpretation of the quality score is at the

discretion of the originator, but the following general

quality interpretations are recommended:

1–25 – unacceptable quality

26–50 – low quality, suitable for veriﬁcation in low-

cost systems

51–75 – medium quality, suitable for veriﬁcation iden-

tiﬁcation (one to many matching) in medium se-

curity applications

76–100 – highest quality images, suitable for

enrollment

Image Capture Recommendations

Appendix A of the standard provides speciﬁc recom-

mendations on capture of iris images, based on vendor

experience in commercial deployments of iris recogni-

tion. These recommendations include the following:

Resolution

Grayscale range

Illumination wavelength

Contrast

Iris visibility

Pixel aspect ratio

Image scale

Optical distortion

Noise content

Image orientation

Subject presentation

ANSI and ISO Differences

Although the American National standard and the

international standard are more or less identical there

Iris Image Data Interchange Formats, Standardization

799