Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов
Подождите немного. Документ загружается.


ПРИЛОЖЕНИЯ
№
1
ДИСПЕРСИЯ ОШИБКИ ПРОГНОЗИРОВАНИЯ
СТОХАСТИЧЕСКОГО ПРОЦЕССА
ТЕЙЛА — ВЕЙДЖА С ПОМОЩЬЮ
ЛИНЕЙНОГО ПРЕДИКТОРА ХОЛЬТА
Г. Тейлом и С. Вейджем [103] было предложено
выражение для
оценки
дисперсии ошибки прогноза на один
iiiar
вперед (т = 1). Здесь мы выводим более общую форму-
лу для любого х ^ 1. Напомним вкратце модель.
Процесс
0)
(2)
М (e
t
vf) = 0 для любой пары (t, f).
Схема прогнозирования:
(3)
(4)
где
ч
(t_ 1) »
Xt
— х
х
(t—\)~ошибка прогноза, сде-
ланного в момент t — 1 на один шаг вперед.
381

Ошибка прогноза, сделанного в момент t на т шагов впе-
ред,
будет:
(5)
где
Ошибка прогноза имеет три источника: ошибку оцен-
ки
коэффициента а
х
в момент t, ошибку оценки коэффици-
ента а
2
в момент / и кумулятивную
сумму
случайных ком-
понент
за промежуток времени (t, t -j- т) с
учетом
их влия-
ния
на точность прогноза.
Используя уравнения адаптации (3), (4) и (5), можно
найти
выражения для ошибок моделирования A
t
и B
t
.
Запишем
(3) в виде:
Затем после простых преобразований для A
t
может быть
записано
следующее
соотношение:
(6)
Тем же путем для B
t
получаем
(7)
Запишем
(6) и (7) в векторной форме:
(8)
где
382

Используя
соотношение (8) п раз, получаем
(9)
Первый
член справа сходится к нулю при п -*» оо (см.
[103]). Объединяем (9) и (5) и получаем
Возводим обе части в квадрат и берем математическое
ожидание:
(10)
где
Выражение (10) можно упростить. Пусть
вычтем
В результате получим
(И)
Выражение (11) можно рассматривать как систему ли-
нейных
уравнений с тремя >
элементами,
s
lb
s
ia
, s
22
матрицы
S. Ясно, что S симметрична, т. е. % = s
ia
.
Можно
(11) записать в развернутой форме:
383:

что эквивалентно
следующему:
Решение
будет
такое:
Возвращаясь к (10) и (11), видим, что дисперсия ошиб-
ки
После подстановки получим искомый
результат:
Дисперсия ошибки прогноза на один шаг вперед D
e
(1)
находится экспериментально в
результате
оптимизации па-
раметров модели.
384

№
2
СОВМЕСТНОЕ АПОСТЕРИОРНОЕ
РАСПРЕДЕЛЕНИЕ ПАРАМЕТРОВ
ЛИНЕЙНОЙ МОДЕЛИ
В приложении дан вывод результатов, исполь-
зуемых
в гл. 6. В разделе А рассматривается общий случай,
в
разделе Б — частный случай линейной модели прогно-
зирования
с
двумя
параметрами.
А. Общий случай
Рассмотрим модель, генерирующую временной ряд, ко-
торая в момент t имеет вид:
(АЛ)
(А.2)
где X
t
является вектором значений, наблюдаемых в момент
t размерности (1x1). Двумерные матрицы L, С и F име-
ют размерности (п X я), (п X р) и (I X п) соответственно.
Вектор параметров A
t
имеет размерность (п X 1). Вектора
e
t
и щ размерности (/ X 1) и (р X 1) соответственно явля-
ются векторами случайных независимых переменных с
математическим ожиданием 0. Предполагается, что зако-
ны
распределения вероятностей e
t
и
и*
и
матрицы F, L
и
С,
соответствующие каждому периоду времени / (/ ^ t +1),
известны, но не оговорено как они изменяются во време-
ни.
X (t — 1) определяется как матрица, состоящая из век-
торов прошлых наблюдений
Х<_1_г
(i
==
1, ..., °о), a A
f
_i
и
e
t
определены как:
(А.З)
(А.4)
По
формуле Байеса, записывая
X(t—l)
как X, сов-
местное распределение вероятностей равно:
(А.5)
где
(А.6)
25
-ш
385
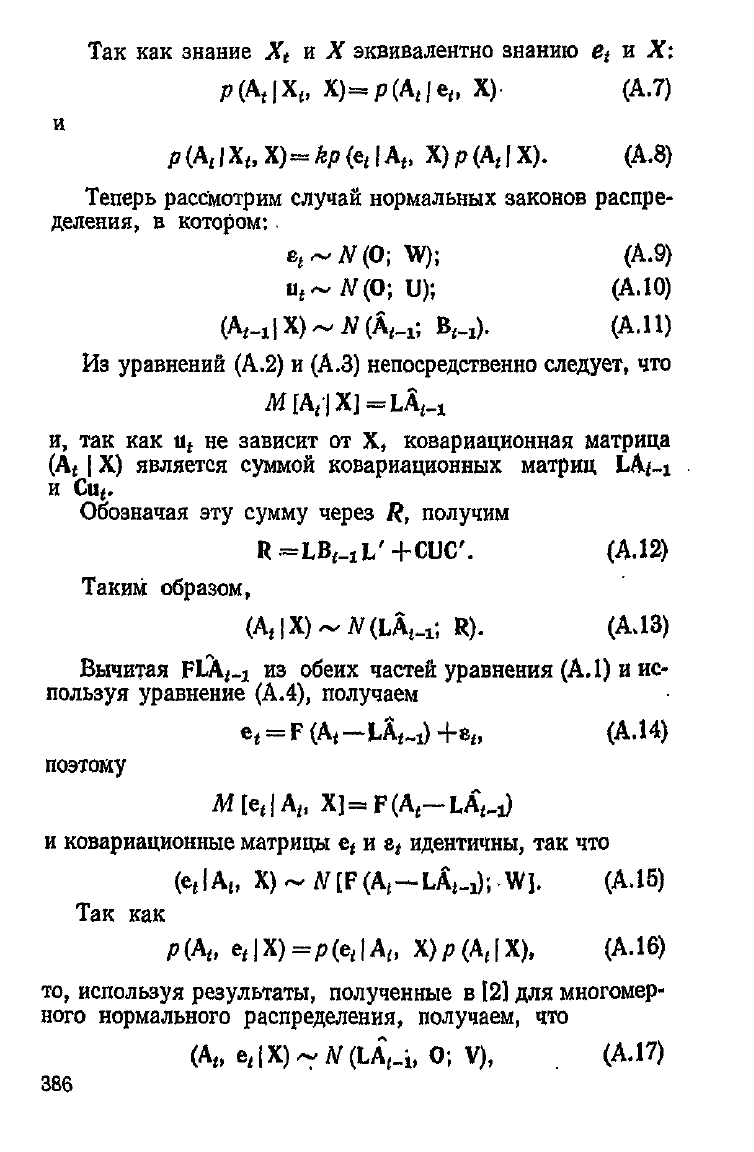
Так как знание
X
t
и X
эквивалентно знанию
e
t
и X:
(А.7)
и
(А.8)
Теперь рассмотрим случай нормальных законов распре-
деления, в котором:
(А.8)
(АЛО)
(А.11)
Из
уравнений (А.2) и (А.З) непосредственно
следует,
что
и,
так как щ не зависит от X, ковариационная матрица
(A
f
| X) является суммой ковариационных матриц
LAf-i
и
Ciif.
Обозначая эту
сумму
через /?, получим
(А. 12)
Таким
образом,
(А.13)
Вычитая
FLA^j
из обеих частей уравнения (АЛ) и ис-
пользуя уравнение (А.4), получаем
(АЛ4)
поэтому
и
ковариационные матрицы e
t
и е* идентичны, так что
(АЛ5)
Так
как
(А Л 6)
то, используя результаты, полученные в [2] для многомер-
ного нормального распределения, получаем, что
(АЛ7)
386

где V может быть записана в расчлененном виде как:
(А.
18)
Аналогично, используя статистические результаты, вы-
веденные для условных многомерных нормальных распре-
делений,
.
получаем
требуемое
распределение вероятностей
A
t
при условии, что заданы все наблюдения до X
t
включи-
тельно, как условное распределение при заданных е
4
и X.
Таким
образом,
(А.19)
где
(А.20)
По
(А.
14)
и (А.
13)
можно заметить, что
так
что W + FRF' является ковариационной матрицей
прогноза, сделанного в момент (t — 1) на один шаг вперед.
Б.
Частный случай
Рассмотрим процесс:
где e
t
, щ, v
t
являются независимыми нормальными случайг
ными
переменными с нулевыми математическими ожидания-
ми
и дисперсиями D
e
> #
u
» &v
В обозначениях рассмотренного выше общего случая:
387
25*

Из
результатов, полученных в общем
случае,
следует,
что если х
(t)
представляет собой все наблюденные значения
до момента t включительно и если
где
то из (19)
где
и
aD
e
=
f%
r
u
+ D
е
является дисперсией ошибки прогноза
на
один шаг вперед.
Величины Гц определены (А. 12) как
где
388

Используя уравнение
(А.20):
и обозначение:
получаем:
№
3
ОЦЕНКА ПАРАМЕТРОВ
В НЕЛИНЕЙНОЙ РЕГРЕССИИ
Очень часто при оценивании экономико-математических
моделей нелинейные модели приходится сводить к линей-
ным
и оценивать уже эти производные модели с помощью
линейных методов.
Предположим, что необходимо оценить параметры про-
изводственной функции типа Кобба—Дугласа:
(1)
Относительно неизвестных параметров А, и, а это урав-
нение
нелинейно и непосредственно применять метод наи-
меньших квадратов (МНК) нельзя. Уравнение (1) преобра-
зуют
в линейное
путем
деления на L и логарифмирования:
(2)
Последнее уравнение уже допускает использование
обычного МНК для оценки параметров In Л, к
и
а. Одна-
ко
если не принять определенных мер (см. П2]
1
), то оценки
1
Так как указанная работа опубликована малым тиражом и
широкому
кругу читателей не известна, повторяем ход рассуждений.
389

параметров вследствие проведенных преобразований ока-
жутся
смещенными.
Запишем
(1) в общем виде:
или
(3)
— теоретическое значение Y
t
;
— эндогенная переменная модели;
— вектор экзогенных переменных;
— вектор неизвестных оцениваемых пара-
метров;
е — случайная ошибка.
Разделим обе части (3) на элемент некоторого ряда Ri
и
получим новое уравнение:
(4)
или
Применение
МНК к уравнению (4) означает минимиза-
цию суммы квадратов новых отклонений щ\
(5)
Из
этого уравнения видно, что после деления обеих час-
тей уравнения (3) на R
t
мы приходим к минимизации сум-
мы квадратов отклонений, отличной от Q — 2е?, которая
минимизируется при непосредственном применении МНК'
к
уравнению (3). Поскольку Q' ф Q, то и вектор оценен-
ных параметров (Г
будет
отличен от ß.
Значения
Щ- являются как бы весами по отношению
к
ошибкам е?. Следовательно, большим значениям R? бу-
дет соответствовать меньшее слагаемое 8?/Я?, входящее в
общую
сумму
Q'. В том
случае,
когда ряд R возрастающий,
ошибки,
соответствующие более ранним моментам времени,
входят
в общую'
сумму
Q' с большим весом, а ошибки неда-
лекого прошлого с меньшим весом, т. е. уравнение регрес-
сии
(4),
будет
лучше
приближать
значения
У*, наблюдавшие-
ся
в первые моменты времени. Таким образом, можно гово-
рить о смещении уравнения регрессии в прошлое.
390
