Лукашук В.С. Нестандартное оборудование вагоносборочного производства. Конструкция, проектирование, расчет
Подождите немного. Документ загружается.

160
Глава 8
ОБОРУДОВАНИЕ ДЛЯ ПОВОРОТА УЗЛОВ
ПРИ ПРОИЗВОДСТВЕ СБОРОЧНО-СВАРОЧНЫХ
РАБОТ
Из практики использования поворотных устройств в сварочных техно-
логических процессах
Существует мнение, что поворотные устройства позволяют придать сварным
швам удобное для сварки положение, за счет чего повышается качество свар-
ного шва. Поскольку качество сварки должно быть обеспечено при любом по-
ложении шва в пространстве, то из этого мнения явно не просматривается
экономическая эффективность использования поворотных устройств.
Рассмотрим простой пример. Пусть требуется соединить две детали ручной
дуговой сваркой электродами марки ЦМ-7, диаметр электрода 4 мм.
Основное время при сварке (время горения дуги) рассчитывают по формуле
t
o
= FLγ/Iα
н
,
где t
o
— основное время; F— площадь сечения наплавленного металла; γ —
плотность наплавленного металла; I — сила сварочного тока; α
н
— коэф-
фициент наплавки, определяющий массу присадочного материала, перешед-
шего в сварной шов за единицу времени при силе сварочного тока в 1 А (вели-
чина постоянная для марки присадочного материала).
При наложении рассматриваемого шва в вертикальном положении сила сва-
рочного тока не должна превышать 160 А. Если изделие повернуть так,
чтобы шов принял нижнее положение, то силу сварочного тока можно уве-
личить до 200 А. При этом основное время уменьшается на 20 %. Экономи-
ческая эффективность использования поворотного приспособления стано-
вится очевидной.
8.1. Одностоечные консольные кантователи
8.1.1. Конструктивные схемы одностоечных кантователей
Консольный одностоечный кантователь с горизонтальной или наклон-
ной осью вращения (рис. 8.1) имеет шпиндель, установленный в корпусе
на подшипниках качения или скольжения. На консольном хвостовике
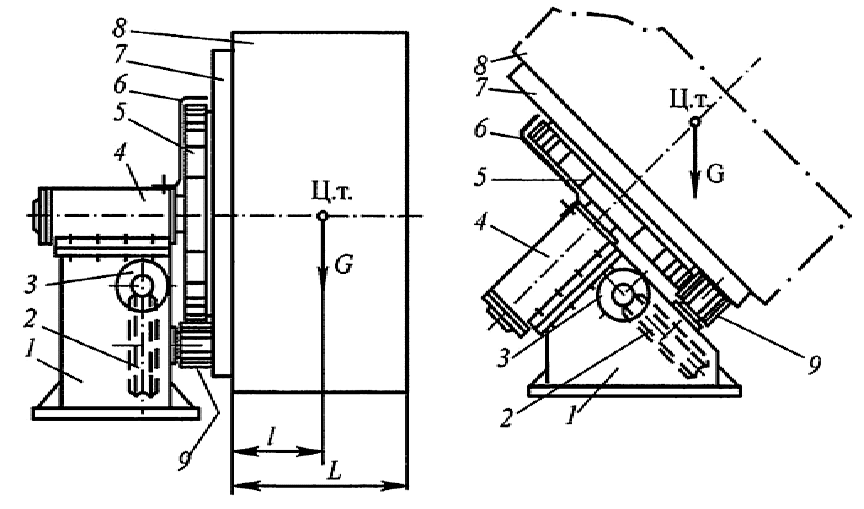
161
Рис. 8.1. Конструкция одностоечных кантователей: а — с горизонтальной осью
вращения; б — с наклонной осью вращения; 1 — станина; 2 — червячный редук-
тор; 3 — электродвигатель; 4 — корпус шпинделя; 5 — зубчатое колесо;
6 — защитный кожух; 7 — крепежная планшайба; 8 — свариваемое изделие;
9 — шестерня
шпинделя насажена крепежная планшайба или другое устройство для креп-
ления свариваемого изделия. Шпиндель приводится во вращение асинхрон-
ным электродвигателем через червячный редуктор и открытую зубчатую
пару. Ведомое колесо открытой зубчатой пары может быть прикреплено к
планшайбе, насажено на консольный конец шпинделя или на среднюю часть
шпинделя в промежутке между подшипниками.
Одностоечные консольные кантователи имеют одну особенность, ог-
раничивающую область их применения. Это заключается в консольном кре-
плении изделия к планшайбе кантователя. Следовательно, нельзя допустить,
чтобы центр тяжести свариваемого изделия был существенно удален от
плоскости планшайбы, так как в этом случае на шпиндель будет действовать
весьма большой изгибающий момент.
Из изложенного следует, что консольные кантователи можно применять
для сварки балок тележек, в ремонтных работах при наплавке изношенных
поверхностей боковин и буртов надрессорных балок тележек грузовых ваго-
нов и в других аналогичных случаях.
В консольных кантователях частоту вращения изделия выбирают в
пределах 0,42...0,84 рад/с (4...8 об/мин) в зависимости от габаритных
размеров свариваемого изделия. Чем меньше габаритные размеры изде-
162
лия, тем большую частоту вращения планшайбы можно принять. При выбо-
ре частоты вращения изделия обычно ориентируются на окружную (линей-
ную) скорость наиболее удаленных от центра поворота точек изделия. Ее
принимают в пределах 0,26...0,42 м/с (16...25 м/мин).
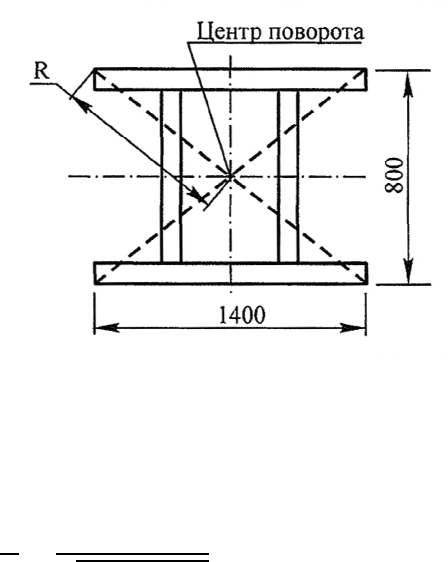
Пример 8.1. Выбрать частоту вращения шпинделя одностоечного кантовате-
ля, применяемого для сварки рамы следующей конструктивной схемы:
Ре ш е н и е
Окружную скорость наиболее удаленных от центра поворота точек рамы при-
нимаем V = 0,33 м/с (20 м/мин). Частота вращения шпинделя
п =
=
0,33
0,7
+0,4
=0,41рад/с(4об/мин).
8.1.2. Расчет одностоечных кантователей с горизонтальным
шпинделем
Расчет одностоечных кантователей сводится к определению потребной
мощности привода кантователя и прочностным расчетам его элементов.
Мощность привода кантователя и его прочность определяются по дейст-
вующим на него усилиям и моментам, выбранной частоте вращения и кине-
матической схеме кантователя.
Расчетные схемы кантователей (рис. 8.2) в зависимости от принятой
кинематической схемы могут быть представлены по одному из двух ва-
риантов. В первом варианте зубчатое колесо закреплено на консольной
части шпинделя или планшайбе. Во втором варианте зубчатое колесо
(см. рис. 8.2, штриховая линия) закреплено на шпинделе между подшип-
никовыми опорами А и В. Расположение зубчатого колеса между опорами
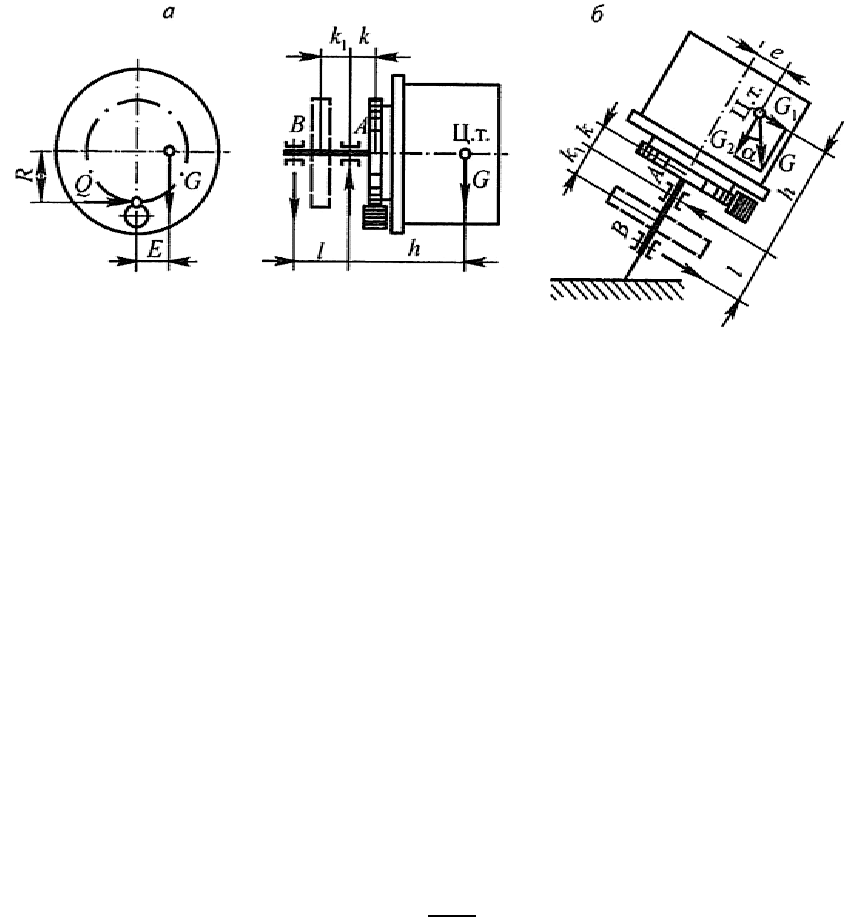
163
Рис. 8.2. Расчетные схемы одностоечных кантователей: а—с горизонтальной осью
поворота; б — с наклонной осью поворота
существенно влияет на величину опорных реакций А и В и величины изги-
бающего и крутящего моментов, действующих на шпиндель.
На величину этих силовых факторов существенно влияет также рас-
положение ведущей шестерни. Лучшей является кинематическая схема
привода кантователя, в которой ведущая шестерня расположена на вер-
тикальной оси привода (над или под зубчатым колесом). В этом случае
усилия и изгибающие моменты от веса G свариваемого узла и окружного
усилия на зубчатом колесе Q суммируются геометрически. При располо-
жении шестерни на горизонтальной оси эти усилия будут суммироваться ал-
гебраически.
Мощность приводного электродвигателя кантователя определяется вы-
ражением
=
М
к
п
сη
о
,(8.1)
где N — потребная мощность электродвигателя, кВт;
М
к
— максимальный крутящий момент, передаваемый зубчатым коле-
сом, Н∙м;
п — частота вращения шпинделя, рад/с;
с — коэффициент, учитывающий размерности входящих в формулу ве-
личин ( с = 101945);
η
о
— общий коэффициент полезного действия (КПД) передачи.
В схеме кантователя, представленной на рис. 8.1,
η
о
= η
з
η
р
= 0,95 ∙ 0,6 = 0,57.
где η
з
= 0,95 — КПД открытой зубчатой передачи;
η
р
= 0,6 — КПД однозаходного червячного редуктора.
164
Максимальный крутящий момент М
к
, преодолеваемый приводом кан-
тователя, равен
М
к
=+М
тр
,(8.2)
где G — вес свариваемого узла совместно с планшайбой;
е — эксцентриситет силы G (см. рис. 8.2);
М
тр
— момент сил трения в подшипниках.
Суммарный момент сил трения в подшипниках (если шпиндель уста-
новлен на подшипниках скольжения) равен
М
тр
=0,5
(
А
А
+В
В
)
,(8.3)
где f — коэффициент трения в подшипниках;
А и В — соответственно реакции (силы) в опорах А и В (см. рис. 8.2);
d
A
, d
B
— диаметры шпинделя в подшипниках А и В.
Если шпиндель смонтирован на подшипниках качения, то вторым сла-
гаемым в выражении (8.2) можно пренебречь.
Реакции в подшипниковых опорах найдем как геометрические суммы их
вертикальных и горизонтальных составляющих:
А =
А
В
+А
Г
;В =
В
В
+В
Г
,(8.4)
где А
В
, В
В
— вертикальные реакции в опорах кантователя, обусловленные
силой G;
А
Г
, В
Г
— горизонтальные реакции в опорах, возникающие от действия
окружного усилия Q на зубчатом колесе.
А
В
=
ℓ +ℎ
ℓ
;В
В
=
ℎ
ℓ
;
(8.5)
А
Г
=
ℓ +
ℓ
;В
Г
=
ℓ
.
Подставив зависимости (8.5) в формулы (8.4), получим выражения для
определения полных усилий в подшипниках А и В:
А =
ℓ +ℎ
ℓ
+
ℓ +
ℓ
;
(8.6)
В =
ℎ
ℓ
+
ℓ
.

165
При расчете момента трения по выражению (8.3) возникает необходи-
мость оперировать диаметрами шпинделя в подшипниках, поэтому диамет-
ры d
A
и d
B
назначают ориентировочно на этапе эскизной проработки канто-
вателя. Далее эти диаметры уточняются по условию прочности шпинделя.
Для кантователей с зубчатым колесом, закрепленным на планшайбе, пер-
вое слагаемое крутящего момента в выражении (8.2) на шпиндель пе-
редаваться не будет. Поэтому диаметр шпинделя в наиболее нагруженном
сечении (опора А) найдем по условию его прочности, исходя из того, что на
шпиндель совместно действуют изгибающий и крутящий моменты:
А
≈
32
М
и
+М
к
[σ]
,(8.7)
где М
и
— изгибающий момент, действующий на шпиндель в опоре А;
М
к
— крутящий момент, определяемый выражением (8.2) с учетом того,
что в некоторых кинематических схемах Ge = 0;
[σ] — допускаемые напряжения растяжения-сжатия для материала
шпинделя (для стали 40Х [σ] = (60...80) Н/мм
2
).
Если шпиндель смонтирован на подшипниках качения и зубчатое колесо
закреплено на планшайбе, то
А
≈
32М
и
[σ]
≈
10М
и
[σ]
.(8.8)
Изгибающий момент М
и
в опоре А равен геометрической сумме двух из-
гибающих моментов, действующих во взаимно перпендикулярных плоско-
стях: грузового момента М
1
= G h и момента от окружного усилия на зуб-
чатом колесе М
2
= Qk.
М
и
=
М
+М
=
(
ℎ
)
+
(
)
,(8.9)
где Q = М
кр
/R (М
кр
здесь рассматривают по полному выражению (8.2) с уче-
том слагаемого Ge).
Подшипники шпинделя рассчитываются обычными методами проек-
тирования деталей машин. Для подшипников скольжения расчет ведется
по допускаемому удельному давлению от реакции в опорах шпинделя и

166
величине рv, где р — удельное давление в подшипнике; v — окружная
скорость на шейке вала. Эта величина ориентировочно характеризует из-
нос и нагрев подшипника.
Условие прочности подшипника скольжения (например, в опоре А) имеет
вид
р
А
=
А
А
ℓ
А
≤[р],
где р
А
— расчетное удельное давление в подшипнике;
ℓ
А
— длина подшипника в опоре А;
[р ] — допускаемое удельное давление, зависящее от назначения ме-
ханизма и условий его работы.
Приводы кантователей можно отнести к классу открытых тихоход-
ных передач. Для машин данного класса [р ] принимают в диапазоне
от 1 до 4 Н/мм
2
.
Условие работоспособности того же подшипника по износу и нагреву
имеет вид
р
А
А
≤[р],
где v
A
— окружная скорость шейки шпинделя в опоре А.
А
=
А
п
1000∙60
м/с,
где d
A
—диаметр шейки шпинделя в опоре А, мм;
п — частота вращения шпинделя, об/мин.
Величина [ р v ] зависит от материалов пары трения и состояния кон-
тактируемых поверхностей. Если подшипник выполнен из оловянной
бронзы (например, Бр.ОФ10—1), а шейка вала незакаленная, то [р v ]
принимают не более 6 Н∙м/(мм
2
∙с).
Отметим, что для кантователей проверка подшипников по величине
[р v ] не обязательна, так как механизм привода кантователя работает пе-
риодически.
Подшипники качения подбираются по диаметрам и удельным нагруз-
кам, приведенным в каталогах на подшипники.

167
Напомним, что изложенный метод расчета относится к кантователям, у ко-
торых зубчатое колесо закреплено на планшайбе. У таких кантователей шпин-
дель практически не нагружен крутящим моментом и работает на изгиб.
Если зубчатое колесо закреплено на шпинделе между опорами А и В (см.
рис. 8.2, штриховая линия), то шпиндель полностью воспринимает не только
грузовой изгибающий момент, но и передает крутящий момент на планшай-
бу. В этом случае общая схема расчета кантователя сохраняется, но некото-
рые расчетные формулы приобретают другой вид.
Расчет потребляемой мощности рассматриваемого кантователя выпол-
няется по предыдущей схеме.
При прочностном расчете шпинделя и выборе подшипников изгибающий
момент в опоре А определяется выражением
М
и
=М
=ℎ.(8.10)
Вертикальные реакции А
В
и В
В
в опорах, как и ранее, определяются вы-
ражением (8.5). Горизонтальные реакции А
Г
и В
Г
будут другими:
А
Г
=
ℓ −
ℓ
;В
Г
=
ℓ
.
Полные усилия в подшипниках А и В тоже изменяются.
А =
ℓ +ℎ
ℓ
+
ℓ −
ℓ
;
(8.11)
В =
ℎ
ℓ
+
ℓ
.
Диаметр шпинделя рассчитывается по формуле (8.7) с учетом того, что
крутящий момент М
к
определен по полному выражению (8.2) с учетом гру-
зового крутящего момента Ge.
8.1.3. Расчет кантователей с наклонным шпинделем
В кантователях с наклонным шпинделем (см. рис. 8.2, б) величина дейст-
вующих усилий и моментов зависит от угла наклона шпинделя α.
При определении мощности привода и расчете шпинделя на прочность
необходимо рассмотреть два критических положения кантователя. В первом
положении центр тяжести изделия расположен наиболее низко. При этом
изгибающий момент, действующий на шпиндель в опоре А, достигает своего

168
максимального значения. Крутящий момент на планшайбе М
к
при таком по-
ложении равен нулю. Следовательно, равно нулю и окружное усилие Q на
зубчатом колесе (если пренебречь трением в подшипниках). Второе поло-
жение характеризуется тем, что центр тяжести изделия расположен на гори-
зонтальной оси так, как это показано на рис. 8.2, а в левой проекции. При
этом крутящий момент, воспринимаемый приводом кантователя, достигает
своего максимального значения, но изгибающий момент не обращается в
нуль.
Для определения мощности приводного двигателя критическим будет
второе положение, однако при расчете шпинделя на прочность не-
обходимо рассмотреть оба положения и выбрать из них наиболее не-
благоприятное.
Рассмотрим первое положение кантователя с зубчатым колесом на
планшайбе. Крутящий момент, учитываемый при расчете шпинделя, равен
только моменту сил трения в подшипниках М
тр
и, следовательно, окружное
усилие Q на зубчатом колесе равно
=
М
тр
,(8.12)
где R — радиус начальной окружности зубчатого колеса.
На шпиндель в опоре А действует одновременно три изгибающих
момента: в вертикальной плоскости моменты M
1
и М
2
от действия сил G
1
и
G
2
и момент М
н
в наклонной плоскости от окружного усилия Q. Моменты
М
1
= G
1
h = Gh sinα и M
2
= G
2
ℓ = Gℓ cosα действуют в одной вертикальной
плоскости. Их алгебраическая сумма составляет общий изгибающий момент
в вертикальной плоскости:
М
в
=М
+М
=(ℎsin+ℓcos).(8.13)
Изгибающий момент, действующий в перпендикулярной наклонной
плоскости:
М
н
=.(8.14)
Результирующий изгибающий момент, действующий на шпиндель в
опоре А, равен
М
и
=
М
в
+М
н
=
(ℎsinα+ℓcosα)
+()
.(8.15)

169
Радиальные опорные реакции в подшипниках, лежащие в вертикаль-
ной плоскости и возникающие под действием внешней силы G
1
и момента
M = G
2
ℓ, приложенного к планшайбе, соответственно равны:
А =
ℓ +ℎ
ℓ
+
ℓ
=
ℓ
[
(ℓ +ℎ)sinα+cosα
]
;
(8.16)
В =−
ℎ
ℓ
+
ℓ
=−
ℓ
(ℎsinα+cosα).
Аксиальная реакция опоры (нагрузка на упорный подшипник)
А
уп
=
=cosα.(8.17)
Момент сил трения в подшипниках
М
тр
=0,5(А
А
+В
В
)+0,5
уп
А
уп
уп
,(8.18)
где f и f
уп
— коэффициенты трения в подшипниках;
d
A
, d
B
, d
уп
— диаметры подшипников.
Для кантователей с зубчатым колесом на планшайбе момент трения в
подшипниках является единственным крутящим моментом, воздейству-
ющим на шпиндель. Поэтому диаметр шпинделя рассчитывается по фор-
муле (8.7), куда подставляются значения М
и
и М
тр
, определенные по фор-
мулам (8.15) и (8.18).
Подшипники шпинделя рассчитываются или подбираются по усилиям А,
В, А
уп
.
Приведенные расчетные формулы справедливы также и для кинема-
тической схемы кантователя с зубчатым колесом, расположенным на шпин-
деле между опорами. Это объясняется тем, что при рассматриваемом поло-
жении груза в кантователе окружное усилие на зубчатом колесе равно нулю
при любом расположении колеса.
Рассмотрим второе положение планшайбы с грузом, при котором она по-
вернута относительно первого положения на угол 90°. Грузовой крутящий
момент М
г
в этом случае будет равен
М
г
=
=sinα.(8.19)
Полный крутящий момент, воздействующий на планшайбу:
М
к
=М
г
+М
тр
,(8.20)
где М
тр
— момент сил трения в подшипниках, определяемый выражением (8.18).
