Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

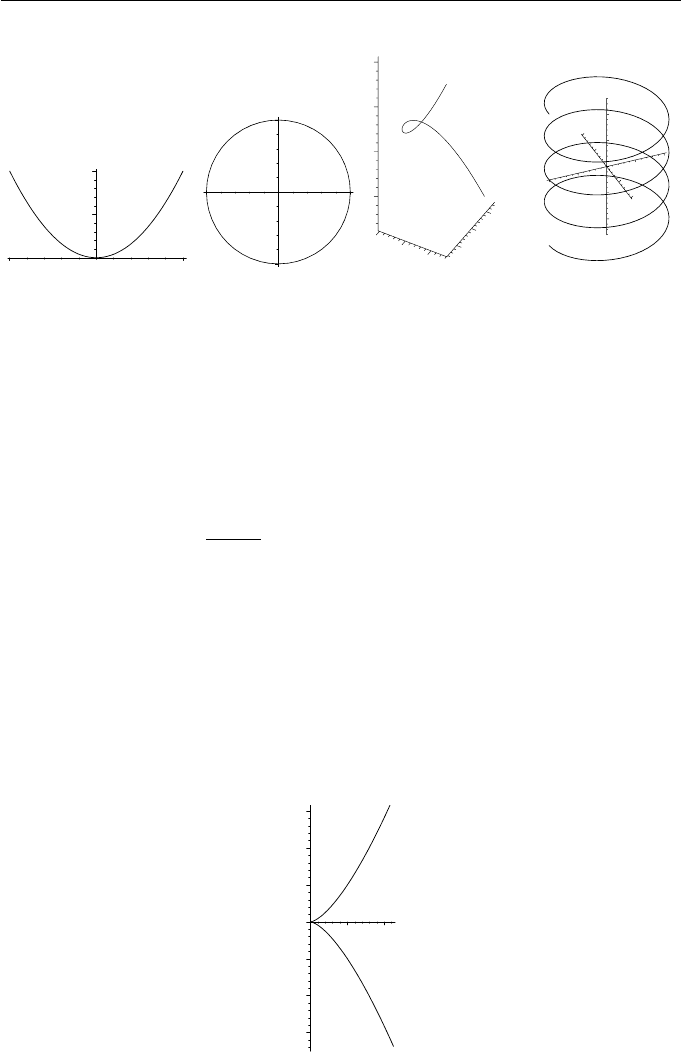
5. Curves 97

0.5

–

–1

–1 1

–1

–20

–10

–20

–10

(a) (b) (c) (d)

Figure 5.1 Parametric curves: (a) parabola, (b) unit circle, (c) twisted

cubic, and (d) helix

Example 5.3 (Non-parametric Implicit Curves)

1. Parabola: y = x

, x ∈ R.

2. Circular arc: y =

√

1 − x

, x ∈ [−1, 1].

3. Twisted space cubic: y = x

, z = x

, x ∈ R.

Example 5.4 (Implicit Curves)

1. Unit radius circle: x

+ y

− 1=0.

2. Cuspidal cubic: y

− x

= 0, see Figure 5.2.

–3

–2

–1

Figure 5.2 Cuspidal cubic y

− x

98 Applied Geometry for Computer Graphics and CAD

5.2 Curve Rendering

The process of drawing a curve is called rendering. Parametric curves are the

most widely used in computer graphics and geometric modelling since points

on the curve are easily computed. In contrast, the evaluation of points on an

implicitly deﬁned curve is substantially more diﬃcult.

A curve of the form C(t)=(x(t),y(t)) deﬁned on the interval [a, b]isren-

dered by evaluating n + 1 points (x(t

),y(t

)), where t

< ···<t

and

= a, t

= b. The points are joined in sequence by line segments to give a

linear approximation to the curve as shown in Figure 5.3. If the resulting ap-

proximation is too jagged then a smoother curve can be obtained by increasing

the number of evaluated points.

(x( ),y( ))tt

i+1 i+1

Figure 5.3 Linear approximation to a parametric curve

Points on polynomial and rational curves can be evaluated using a reason-

able number of arithmetical operations. Points on curves deﬁned by functions

such as square roots, trigonometric functions, exponential and logarithmic func-

tions are more computationally expensive to calculate.

The most economical way to evaluate a polynomial is to use Horner’s

method. Consider the polynomial 1 + 2t +3t

+4t

. If the polynomial is com-

puted as 1 + 2 ·t +3·t ·t +4·t ·t ·t then 3 additions and 6 multiplications are

required. However, if the polynomial is computed as ((4 · t +3)· t +2)· t +1,

then only 3 additions and 3 multiplications are required yielding a saving of 3

multiplications. For polynomials of higher degree the saving is even greater.

In general, a polynomial of the form a

+ a

t + a

+ ···+ a

can be

expressed in the form

(((a

t + a

n−1

) t + a

n−2

) t + ···) t + a

A computer algorithm to evaluate a polynomial, based on Horner’s method, is

easily implemented.

5. Curves 99

EXERCISES

5.1. Express 3−5t+4t

−2t

+6t

in Horner’s form. Determine the diﬀer-

ence in the number of ± and × required to evaluate the polynomial

in its original and new form.

5.2. Write a computer program which takes as input the coeﬃcients of a

polynomial and a parameter value t, and which outputs the value of

the polynomial at the given parameter value using Horner’s method.

5.3. Determine the number of operations ± and × saved by evaluating a

polynomial of degree n using Horner’s method.

5.4. Write a computer program which renders a parametric curve. Alter-

natively, learn how to plot curves using a computer package. Plot

some of the curves given in the examples.

5.3 Parametric Curves

Let C(t)=(x(t),y(t)) be a curve deﬁned on an open interval (a, b). Then C(t)

is said to be C

-continuous (or just C

) if the ﬁrst k derivatives of x (t)andy (t)

exist and are continuous. If inﬁnitely many derivatives exist then C(t)issaidto

be C

∞

.AcurveC(t)=(x(t),y(t)) deﬁned on a closed interval [a, b]issaidto

be C

-continuous if there exists an open interval (c, d) containing the interval

[a, b], and a C

-continuous curve D(t)deﬁnedon(c, d), such that C(t)=D(t)

for all t ∈ [a, b]. Curves deﬁned on a closed interval need to be “extendable”

to a curve on an open interval in order to diﬀerentiate x(t)andy(t)atthe

ends of the interval. (Another type of continuity called G

-continuity, which is

important for CAD applications, is introduced in Deﬁnition 7.14.)

Suppose C(t)isaC

curvedeﬁnedonanintervalI, then the function

ν(t)=





(t))

+(y



(t))

is called the speed of the curve C(t). If ν(t) =0,

for all t ∈ I,thenC(t)issaidtobearegular curve. If ν(t) = 1 for all t ∈ I,

then C(t)issaidtobeaunit speed curve.

Example 5.5

1. Let (x(t),y(t)) = (t, t

). Then (x



(t),y



(t)) = (1, 2t), and

ν(t)=



+(2t)



1+4t

100 Applied Geometry for Computer Graphics and CAD

2. Let (x(t),y(t),z(t)) = (cos t, sin t, t

). Then



(t),y



(t),z



(t)) = (−sin t, cos t, 2t) ,

and

ν =



(−sin t)

+(cost)

+(2t)



1+4t

Let C(t)=(x(t),y(t)) be a regular parametric curve, and suppose P and Q

are the points with coordinates (x(t),y(t)) and (x(t+δt),y(t+δt)) respectively.

Let

δt

−−→

δt

(x(t + δt),y(t + δt)) − (x(t),y(t))

δt

asshowninFigure5.4.Thenasδt → 0, Q → P and t

δt

tends to the limiting

vector

lim

δt→0

δt



lim

δt→0

x(t + δt) − x(t)

δt

, lim

δt→0

y(t + δt) − y(t)

δt



=(x



(t),y



(t)) .



(t)=(x



(t),y



(t)) is called the tangent vector.Theunit tangent vector is

deﬁned to be

t(t)=

|(x



(t),y



(t))|



(t),y



(t)) =





(t)





(t)

+ y



(t)



(t)





(t)

+ y



(t)



The line through the point (x(t),y(t)) in the direction of the tangent vector is

called the tangent line and has the equation



(t)(x − x(t)) − x



(t)(y − y(t)) = 0 . (5.1)

C()t

PQ/dt

Figure 5.4 Tangent and normal to a curve

If the tangent vector C



(t)=(x



(t),y



(t)) is rotated through an angle π/2

radians (in an anticlockwise direction), then the normal vector (−y



(t),x



(t))

is obtained. The unit normal vector of C(t) is deﬁned to be

n(t)=

(−y



(t),x



(t))

|(−y



(t),x



(t))|



−y



(t)





(t)

+ y



(t)



(t)





(t)

+ y



(t)



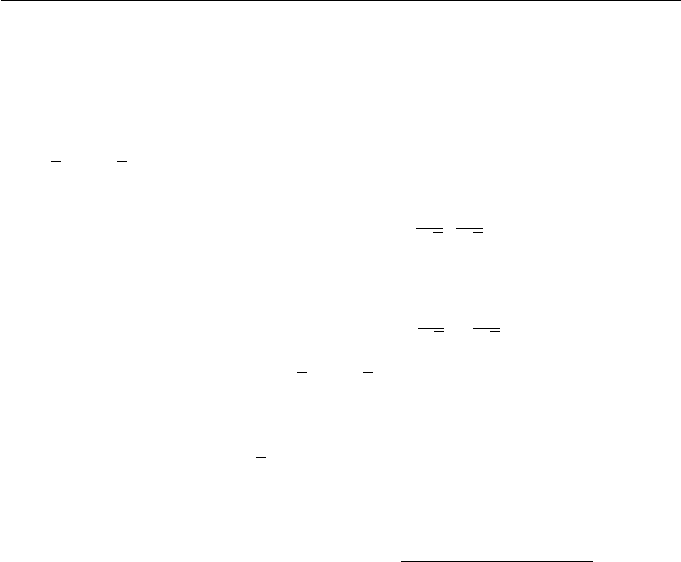
5. Curves 101

Example 5.6

Let C(t) = (cos(t), sin(t)). Then the tangent vector is C



(t)=(−sin(t), cos(t))

and the normal vector is (−cos(t), −sin(t)). Since |C



(t)| = 1 these vectors are

also the unit tangent and normal vectors. At the point (cos(π/4), sin(π/4)) =





√

2 , 1



√



the unit tangent vector is

(−sin(π/4), cos(π/4)) =



−

√



and the unit normal vector is

(−cos(π/4), −sin(π/4)) =



−

√

, −

√



The tangent line to C(t)at





√

2 , 1



√



cos(π/4)(x − cos(π/4)) + sin(π/4)(y − sin(π/4)) = 0 ,

which simpliﬁes to x + y −

√

2=0.

The derivation of the tangent vector can be extended to space curves: for a

curve C(t)=(x(t),y(t),z(t)), the tangent vector is C



(t)=(x



(t),y



(t),z



(t)),

and the unit tangent vector is t(t)=C



(t)/





(t)

+ y



(t)

+ z



(t)

EXERCISES

5.5. Let C(t)=(x(t),y(t)) be a regular curve.

(a) Determine the parametric equation of the tangent line to C at

the point (x(t),y(t)).

(b) Prove that the tangent line to C(t)atapoint(x(t),y(t)) is given

by Equation (5.1).

through p perpendicular to the tangent. Determine the implicit

equation of the normal line.

5.6. For each of the curves below, determine (i) the unit tangent vector,

(ii) the unit normal vector, and (iii) the implicit equation of the

tangent line.

(a) (t, t

)atthepoint(1, 1).

(b) (t

) at the point (4, 8).

102 Applied Geometry for Computer Graphics and CAD



cos t, ae

sin t



(d) cycloid: (t +sint, 1 − cos t).

(e) (cos t + t sin t, sin t − t cos t).

(f) catenary: (c cosh (t/c) ,t).

5.7. Show that a translation of a curve has no eﬀect on the speed of a

curve.

5.8. Show that a rotation has no eﬀect on the speed of a curve.

5.4 Arclength and Reparametrization

Consider the following three parametrizations of the unit quarter circle (in the

ﬁrst quadrant) centred at the origin.

(1) (cos

t, sin

t),t∈ [0, 1],

(2)



1−t

1+t



,t∈ [0, 1], and

(3)



√

1 − t



,t∈ [0, 1].

(a) (b) (c)

Figure 5.5 Diﬀerent parametrizations of the quarter circle: (a)

(cos

t, sin

t), (b)



1−t

1+t



, and (c)



√

1 − t



Figure 5.5 shows the three parametrizations of the quarter circle evaluated

at 15 equal parameter increments t

= i/14, for i =0,...,14. For parametriza-

tion (1) the points are equally spaced along the arc, for (2) the points are quite

evenly spaced, and for (3) the points are unevenly spaced. The diﬀerence in

the behaviour of the parametrizations corresponds to the fact that in (1) each

5. Curves 103

parameter interval [t

i+1

] maps to a circular arc of equal length, whereas in

(2) and (3) the parameter intervals map to circular arcs of varying lengths.

To explore this further a method to calculate the length of a curve is re-

quired. Consider a regular curve C(t)=(x(t),y(t)), for t ∈ [a, b], and a sequence

of equally spaced parameter values t

= a +

(b − a) (for i =0,...,n) with

= a and t

= b. The line segment from (x(t

),y(t

)) to (x(t

i+1

),y(t

i+1

))

approximates the curve on the interval [t

i+1

] and has length



(x(t

i+1

) − x(t

))

+(y(t

i+1

) − y(t

))

Thus the length L (C)ofthecurveC on the interval [a, b] is approximately

n−1



i=0



(x(t

i+1

) − x(t

))

+(y(t

i+1

) − y(t

))

. (5.2)

If the parameter increments δt = t

i+1

− t

=(b − a)/n are suﬃciently small,

then x



) is approximately equal to (x(t

i+1

) − x(t

))/ (t

i+1

− t

), y



)isap-

proximately equal to (y(t

i+1

) − y(t

))/ (t

i+1

− t

), and substitution into (5.2)

yields that L (C) is approximately

n−1



i=0





))

+(y



))

δt . (5.3)

The true length of the curve over [a, b] is realized by letting n tend to inﬁnity.

As n increases the line segments ﬁt the curve more closely, and (5.3) becomes

a better approximation to the length of the curve. The limit of (5.3) as n tends

to inﬁnity is

L(C)=







(t))

+(y



(t))

dt =



ν(t) dt .

L(C) is called the arclength of C(t)fromt = a to t = b.Thearclength function

(t)=







(u)

+ y



(u)

du,fora ≤ t

≤ b, measures the length of the

curve segment from an initial point (x(t

),y(t

)) to the point (x(t),y(t)). Then

L(C)=L

(b) − L

(a).

Example 5.7

1. The speed of the quarter circle C(t)=(cost, sin t), for t ∈





,is

ν(t)=



(−sin t)

+(cost)

= 1. The parametrization is unit speed and

the arclength function from t

=0isL

(t)=



1 du = t.Thecurvehas

length L





− L

(0) =

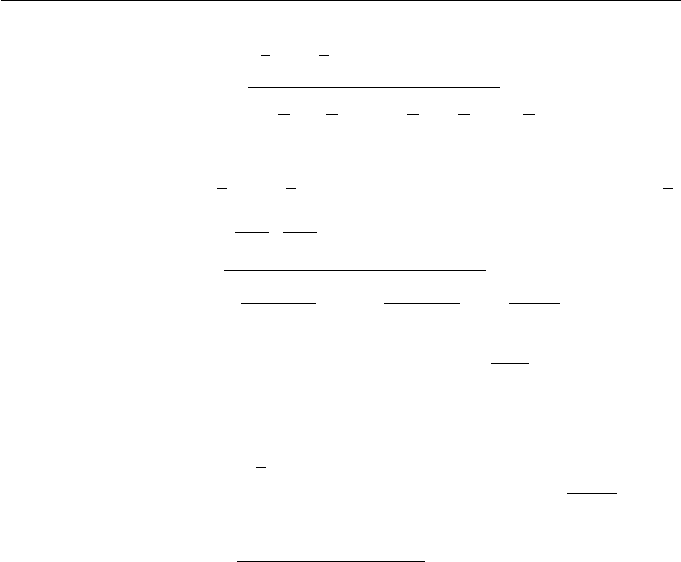
104 Applied Geometry for Computer Graphics and CAD

2. The speed of C(t)=(cos

t, sin

t), for t ∈ [0, 1], is

ν(t)=





−

sin





cos



The parametrization has constant speed and the arclength function from

=0isL

(t)=



du =

t. The curve has length L

(1) −L

(0) =

3. The speed of C(t)=



1−t

1+t



,fort ∈ [0, 1], is

ν(t)=





−4t

(1 + t

)





2(1 − t

)

(1 + t

)



1+t

and the arclength function from t

=0isL

(t)=



1+u

du = 2 arctan(t).

Thus, with this parametrization, the unit quarter circle starts at point (1, 0)

with speed ν(0) = 2. As t increases the speed decreases until the curve

reaches the point (0, 1) when the curve has speed ν(1) = 1. The curve has

length L

(1) − L

(0) =

4. Let the unit quarter circle be parametrized by C(t)=



√

1 − t



,for

t ∈ [0, 1]. Then (x



(t),y



(t)) = (−t(1 − t

)

−1/2

, 1), and

ν(t)=





−t(1 − t

)

−1/2



+ 1 =(1 − t

)

−1/2

Thus, with this parametrization, the unit quarter circle starts at point (1, 0)

with speed ν(0) = 1. As t increases the speed increases until the curve

reaches the point (0, 1) when the curve has inﬁnite speed. The arclength is

computed in Exercise 5.9.

The arclength functions of the three parametrizations of the quarter circle

are illustrated in Figure 5.6. In each plot the vertical axis shows the length

of the curve traced from (x(0),y(0)) to (x(t),y(t)). Naturally, the total curve

length in each case is π/2. Parametrization (1) traces the curve uniformly. The

speed of parametrization (2) is decreasing, so the curve is traced more quickly

in the beginning than at the end. The speed of parametrization (3) is increasing

so the curve is traced more quickly at the end than at the beginning.

Deﬁnition 5.8

Let C(t)andD(t) be curves deﬁned on intervals I and J respectively. Then D

is said to be a reparametrization of C if there exists a diﬀerentiable function

h : J → I such that h



(t) =0andD(t)=C(h(t)) for all t ∈ J. The function

h(t)isreferredtoasareparametrization.

5. Curves 105

0.5

1.5

0.5

1.5

0.5

1.5

(a) (b) (c)

Figure 5.6 Comparison of the arclength functions of three parametriza-

tions of the quarter circle

Example 5.7(1) is a unit-speed parametrization of the unit quarter circle.

Parametrization (1) can be obtained from the unit speed parametrization by a

reparametrization with h(t)=

t and J =[0, 1]. Parametrizations (2) and (3)

are also reparametrizations of the unit speed quarter circle. The next theorem

shows that the arclength function can be used to reparametrize a curve to give

a unit speed curve with the same trace.

Theorem 5.9

Let C(t)=(x(t),y(t)) be a regular curve deﬁned on an interval I with arclength

function s(t)=L

(t). Then C(s)=



−1

(s)





−1

(s)



is a unit speed

curve.

Proof

Let s = L

(t). Diﬀerentiating with respect to t gives L



(t)=|C



(t)| = ν(t).

Since C(t) is regular, L



(t) = 0 for all u ∈ I, and the inverse function theorem

implies that the inverse t = L

−1

(s) exists. Let h(s)=L

−1

(s). Then

1/L



=0,andt = h(s) may be used to reparametrize C(t) to give the curve

C(s)=C(L

−1

(s)) =



−1

(s)





−1

(s)



. Then the chain rule gives

(s)=

−1

(s)



−1

(s)





−1

(s)



106 Applied Geometry for Computer Graphics and CAD

and



(s)



−1

(s)





−1

(s)





−1

(s)







(t)





(t)| =



(t)|



(t)| =1.

Hence

C(s) is unit speed, and the proof is complete.

Example 5.10

Consider parametrization (3) of the unit quarter circle. Exercise 5.9 will deter-

mine the arclength function to be s = arcsin(u). Substituting t = sin(s)into



√

1 − t



gives the unit speed parametrization of the circle (cos(s), sin(s)).

EXERCISES

5.9. Show that the arclength function of C(t)=



√

1 − t



,t∈ [0, 1] is

(t) = arcsin t (assume arcsin has range



−

π,



5.10. Determine the speed and arclength function for each of the following

curves

(a) cycloid: (t +sint, 1 − cos t), t ∈ [−π, π].

(b) (cos t + t sin t, sin t − t cos t), t>0.

(d) astroid:



cos

t, sin



, t ∈ [0,π/2].

(e) logarithmic spiral:



cos t, ae

sin t



5.11. Determine the length of the cycloid and the astroid of the previous

exercise.

5.12. Write a program to determine the arclength of a curve using the

summation formula (5.2) to within a user speciﬁed accuracy >0.

This is achieved by increasing the number of increments n until the

diﬀerence between successive computed approximate lengths is less

than .

5.13. Determine the unit speed parametrization of the unit quarter cir-

cle from parametrization (2) by reparametrizing with the arclength

function.