Marsh D. Applied Geometry for Computer Graphics and CAD

Подождите немного. Документ загружается.

Projections and the Viewing Pipeline

4.1 Introduction

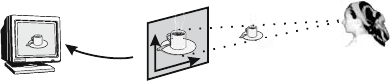
This chapter describes the process of visualizing three-dimensional objects.

Current display devices such as computer monitors and printers are two-

dimensional, and therefore it is necessary to obtain a planar view of the object

which gives the impression of the omitted third dimension. Visualization of an

object is achieved by a sequence of operations called the viewing pipeline (see

Figure 4.1). Firstly, a projection is applied which maps the object to a new

“ﬂat” object in a speciﬁed plane known as the viewplane. The “ﬂat” object

represents a planar view of the object expressed in three-dimensional world

coordinates. Secondly, a coordinate system in the viewplane is deﬁned by spec-

ifying a point as origin, and two perpendicular vectors which give the directions

of the coordinate axes. A viewplane coordinate mapping is applied to express

the “ﬂat” object in terms of the chosen two-dimensional viewplane coordinate

system. Finally, the “ﬂat” object is mapped to the computer screen by means

of a two-dimensional device coordinate transformation.

Projection

Device

coordinate

transformation

Viewplane

Figure 4.1 The viewing pipeline

68 Applied Geometry for Computer Graphics and CAD

The discussion begins in Section 4.2 with projections of the plane onto a

line, and is followed by projections of three-dimensional space onto a plane in

Section 4.3. Section 4.4 introduces the viewplane coordinate mapping which

converts the three-dimensional world coordinate deﬁnition of the view to two-

dimensional coordinates. The ﬁnal step of mapping the view to the display

device is discussed in Section 4.5. In Section 11.6, projections are used to create

shadows which arise when light sources illuminate objects in a scene.

4.2 Projections of the Plane

A view of a spatial object is obtained by a mapping or projection of three-

dimensional space onto a plane. Consider ﬁrst the simpler problem of projecting

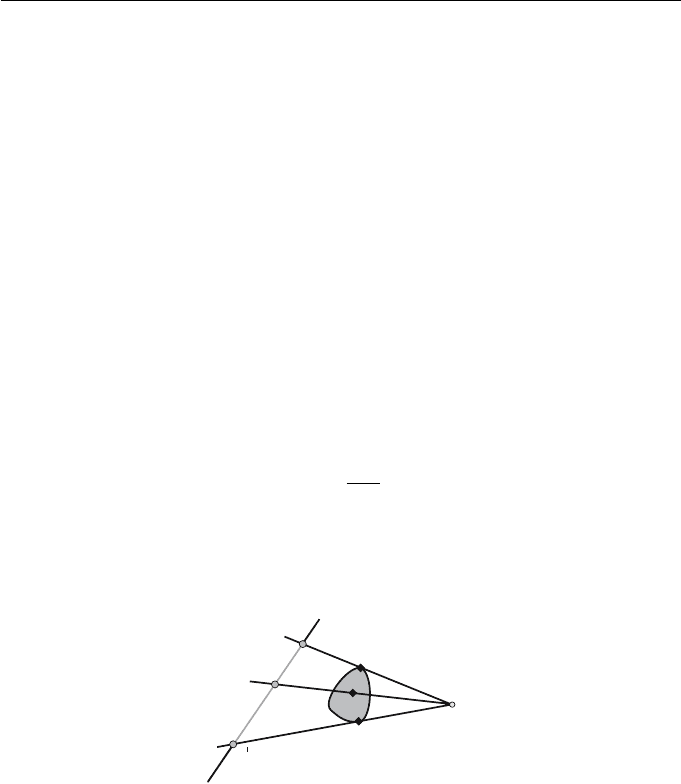
the plane onto a line contained in the plane. Let  be a line in the plane, and

let V be a point not on the line. The perspective projection from V onto  is

the transformation which maps any point P, distinct from V, onto the point



which is the intersection of the lines VP and , as illustrated in Figure 4.2.

The point V is called the viewpoint or centre of perspectivity, and the line 

is called the viewline. The next theorem shows that this mapping is indeed a

transformation.

Figure 4.2 Perspective projection from the viewpoint V onto the line 

Theorem 4.1

The perspective projection from the viewpoint V (expressed in homogeneous

coordinates) onto the viewline with line vector  is the two-dimensional trans-

formation given by the matrix

M = 

V − ( · V)I

where I

denotes the 3 × 3 identity matrix.

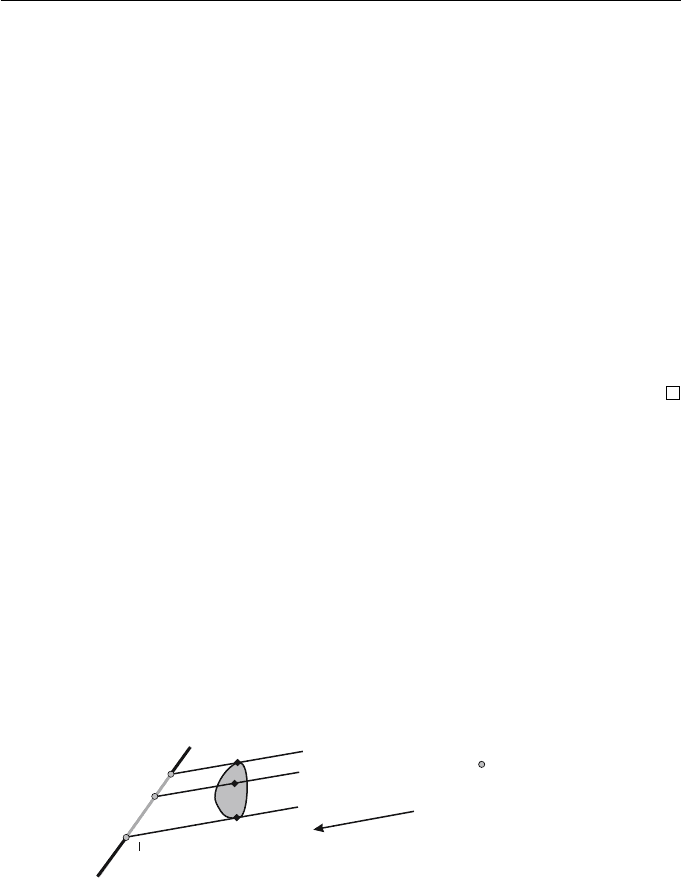
4. Projections and the Viewing Pipeline 69

Proof

Referring to Figure 4.2, the image P



of a point P is obtained as the intersection

of the viewline  with the line through V and P. The techniques of Section 2.7

imply that the line through V and P has the line vector V × P, and therefore

intersects  in the point with homogeneous coordinates given by  × (V × P).

Applying the vector identity A × (B × C)=(C · A) B − (A · B) C yields



=  × (V × P)=(P · ) V − ( · V) P .

Replacing vectors by row matrices, and the dot product by a matrix multipli-

cation, yields



= P

V − P ( · V)I

= P





V − ( · V)I



Thus P



= PM,whereM = 

V − ( · V)I

as required.

Deﬁnition 4.2

The matrix M is called the projection matrix of the perspective projection from

V onto . Lines through the viewpoint are called projectors. The viewpoint

V can be a point at inﬁnity in which case the projection is called a parallel

projection. It is common practice to use the term “perspective projection” to

mean a non-parallel projection.

For a parallel projection with viewpoint V (v

, 0) the projectors corre-

spond to parallel lines in the Cartesian plane with direction (v

)asshown

in Figure 4.3.

(at infinity)

( , ,0)vv

( , ,0)v v

(,)vv

(,)v v

Figure 4.3 Parallel projection in the direction (v

) onto the line 

Example 4.3

The perspective projection of the triangle with vertices A(2, 3), B(4, 4), and

C(3, −1) onto the line 5x + y − 4 = 0 from the viewpoint with Cartesian

coordinates (10, 2) is illustrated in Figure 4.4. The homogeneous viewpoint is

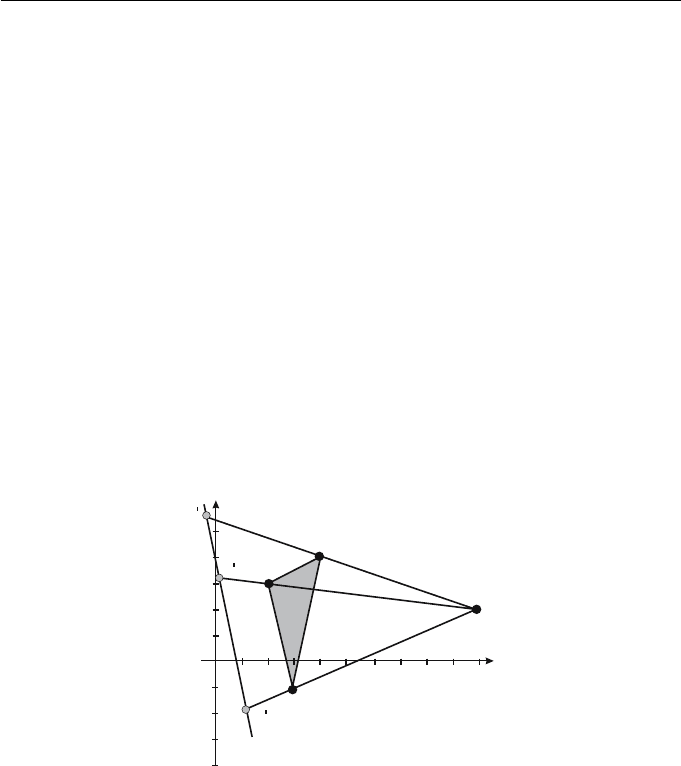
70 Applied Geometry for Computer Graphics and CAD

V (10, 2, 1), the line vector is  =(5, 1, −4), and ·V =(5, 1, −4)·(10, 2, 1) = 48.

Hence

M =

⎛

⎝

−4

⎞

⎠



10 2 1



− 48

⎛

⎝

100

010

001

⎞

⎠

⎛

⎝

50 10 5

10 2 1

−40 −8 −4

⎞

⎠

−

⎛

⎝

48 0 0

0480

0048

⎞

⎠

⎛

⎝

210 5

10 −46 1

−40 −8 −52

⎞

⎠

The images of the vertices are obtained by multiplying the homogeneous coor-

dinates of A, B,andC by M.Then

⎛

⎝



⎞

⎠

⎛

⎝

⎞

⎠

M =

⎛

⎝

231

441

3 −11

⎞

⎠

M =

⎛

⎝

−6 −126 −39

8 −152 −28

−44 68 −38

⎞

⎠

The Cartesian coordinates of the vertex images are A



(6/39, 126/39),



(−8/28, 152/28), and C



(44/38, −68/38).

0123456789100 1 2 3 4 5 6 7 8 9 10

-1

-2

-3

-4

-1

-2

-3

-4

Figure 4.4 Perspective projection of Example 4.3

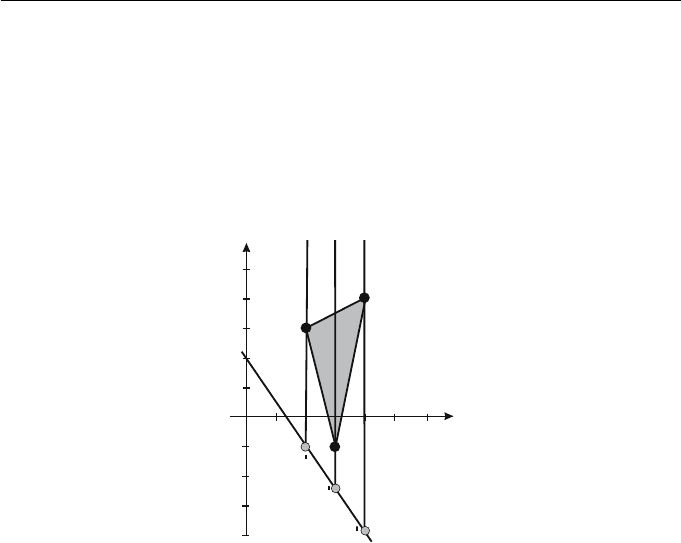
Example 4.4

The parallel projection of the triangle with vertices A(2, 3), B(4, 4), and

C(3, −1) onto the line 3x +2y − 4 = 0 in the direction of the y-axis is shown

in Figure 4.5. The viewpoint is V (0, 1, 0), the point at inﬁnity in the direction

of the y-axis. Then  =(3, 2, −4), and  · V =(3, 2, −4) · (0, 1, 0) = 2. Thus

M =

⎛

⎝

−4

⎞

⎠



010



− 2

⎛

⎝

100

010

001

⎞

⎠

⎛

⎝

−23 0

000

0 −4 −2

⎞

⎠

4. Projections and the Viewing Pipeline 71

and

⎛

⎝



⎞

⎠

⎛

⎝

231

441

3 −11

⎞

⎠

⎛

⎝

−23 0

000

0 −4 −2

⎞

⎠

M =

⎛

⎝

−42−2

−88−2

−65−2

⎞

⎠

Thus the Cartesian coordinates of the images are A



(2, −1), B



(4, −4), and



(3, −5/2).

-1

-2

-3

-4

-1

-2

-3

-4

01234560 1 2 3 4 5 6

Figure 4.5 Parallel projection of Example 4.4

EXERCISES

4.1. Determine the projection matrix for a perspective projection with

viewpoint (2, 11) and viewline −3x +12y − 5=0.

4.2. Determine the projection matrix for a parallel projection in the di-

rection (3, −2) and viewline 7x − 5y − 2=0.

4.3. Determine the projection matrix for a perspective projection with

viewpoint (7, −3) and viewline x − y + 9 = 0. Apply the projection

to the triangle with vertices A(2, 2), B(4, 3), and C(3, 5). Make a

sketch showing the projection of the triangle onto the line.

4.4. Determine the projection matrix for a parallel projection in the di-

rection (−1, 4) and viewline 2x − y + 8 = 0. Apply the projection

to the triangle with vertices A(2, 2), B(4, 3), and C(3, 5). Make a

sketch showing the projection of the triangle onto the line.

4.5. Let P =(p

), V =(v

), and  =(a, b, c). Write out the

proof of Theorem 4.1 in full.

72 Applied Geometry for Computer Graphics and CAD

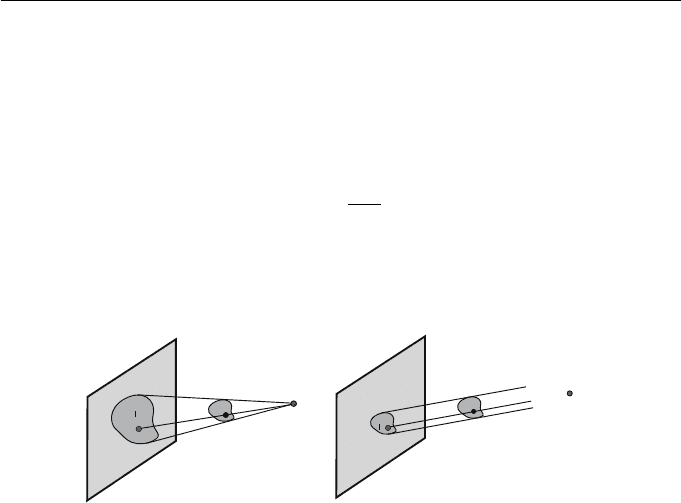
4.3 Projections of Three-dimensional Space

Projections of three-dimensional space follow a similar line of development to

projections of the plane. Let n be the plane vector of a viewplane, and let V

be a point not on the viewplane. The perspective projection from V onto n is

the transformation which maps any point P, distinct from V, onto the point



which is the intersection of the line VP and the plane n, as illustrated in

Figure 4.6(a). If V is a point at inﬁnity then the projection is called a parallel

projection, as illustrated in Figure 4.6(b). The term “perspective projection”

is generally used to mean a projection which is not parallel.

(a) (b)

Viewplane

(at infinity)(at infinity)

Figure 4.6 Perspective and parallel three-dimensional projections

Theorem 4.5

The projection with homogeneous viewpoint V and viewplane with plane vector

n is the three-dimensional transformation given by the matrix

M = n

V − (n · V)I

where I

denotes the 4 × 4 identity matrix,

⎛

⎜

⎝

(−n

−n

− n

)

(−n

−n

− n

)

(−n

−n

− n

)

(−n

−n

− n

)

⎞

⎟

⎠

4. Projections and the Viewing Pipeline 73

Proof

Let P be an arbitrary point to be projected (P = V). If n ·P =0,thenP is a

point on the viewplane and its projected image is P.ToverifythatPM = P,

note that n · P = Pn

= 0 (representing vectors by row matrices), and hence

PM = Pn

V − P(n · V)I

= −P(n · V)I

Since −P(n · V)I

is a multiple of P, PM are homogeneous coordinates of P,

that is, P



= PM.

Suppose n · P = 0. Then every point on the line through P and V has

homogeneous coordinates of the form αP+βV for some α and β (Exercise 3.6).

The line intersects the viewplane when n · (αP + βV)=0.Thenα (n · P)+

β (n · V) = 0, giving α = −β (n · V)/(n · P) = 0. Substituting for α, the point

of intersection is found to have homogeneous coordinates



= αP + βV =(−β (n · V)/(n · P))P + βV .

Multiplying the coordinates by the scalar (n · P) gives the alternative homoge-

neous coordinates



=(n · P) V − (n · V) P .

Then, in matrix form,







V − P (n · V) I

= P



V − (n · V)I



Hence

M = n

V − (n · V)I

Example 4.6

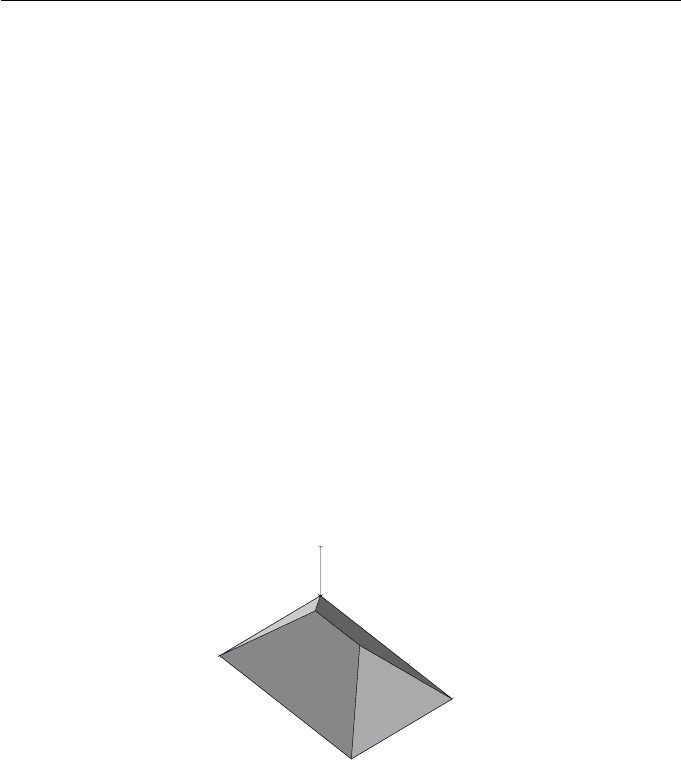
Consider a parallel projection of the prism shown in Figure 4.7 onto the plane

z = 0 in a direction parallel to the z-axis. The viewpoint is V (0, 0, 1, 0), the

point at inﬁnity in the direction of the z-axis, and the viewplane has the equa-

tion 0x +0y +1z +0=0,so n =(0, 0, 1, 0). Thus

M =

⎛

⎜

⎝

⎞

⎟

⎠



0010



−1

⎛

⎜

⎝

1000

0100

0010

0001

⎞

⎟

⎠

⎛

⎜

⎝

−1000

0 −10 0

0000

000−1

⎞

⎟

⎠

74 Applied Geometry for Computer Graphics and CAD

The prism has vertices A(0, 0, 0), B(2, 0, 0), C(2, 3, 0), D(0, 3, 0), E(1, 2, 1),

F(1, 1, 1). Applying the projection to the vertices of the prism gives

⎛

⎜

⎝



⎞

⎟

⎠

⎛

⎜

⎝

0001

2001

2301

0301

1211

1111

⎞

⎟

⎠

⎛

⎜

⎝

−1000

0 −10 0

0 000

000−1

⎞

⎟

⎠

⎛

⎜

⎝

000−1

−200−1

−2 −30−1

0 −30−1

−1 −20−1

−1 −10−1

⎞

⎟

⎠

Following the usual procedure of dividing each point by its fourth coordinate

yields the Cartesian coordinates A



(0, 0, 0), B



(2, 0, 0), C



(2, 3, 0), D



(0, 3, 0),



(1, 2, 0), F



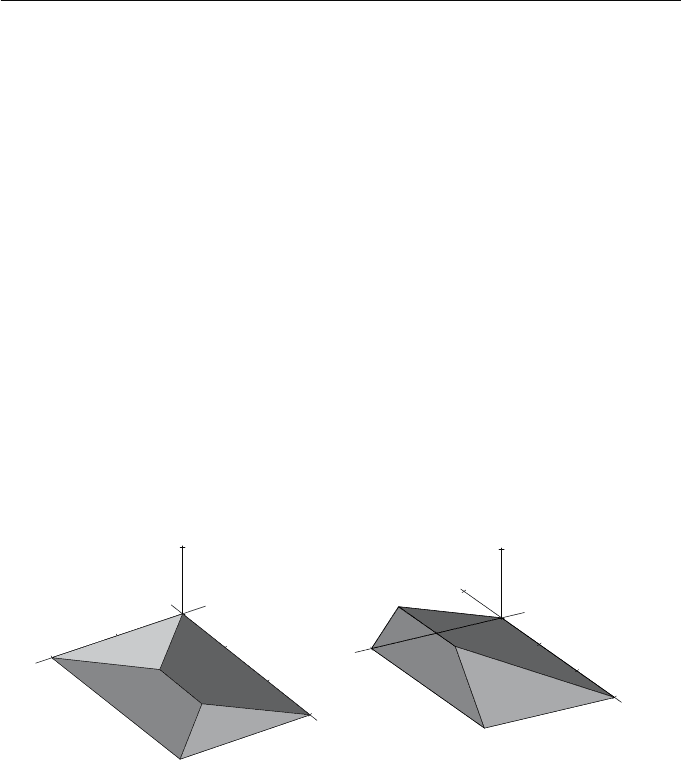
(1, 1, 0). The image of the prism is shown in Figure 4.8(a).

Figure 4.7 Prism of Example 4.6

Example 4.7

Consider a perspective projection onto the plane z = 0 from the viewpoint

(1, 5, 3). The viewpoint has homogeneous coordinates V (1, 5, 3, 1) and the view-

plane vector is n =(0, 0, 1, 0). Thus

M =

⎛

⎜

⎝

⎞

⎟

⎠



1531



−3

⎛

⎜

⎝

1000

0100

0010

0001

⎞

⎟

⎠

⎛

⎜

⎝

−3000

0 −30 0

1501

000−3

⎞

⎟

⎠

4. Projections and the Viewing Pipeline 75

Applying the projection to the vertices of the prism of Example 4.6 yields

⎛

⎜

⎝



⎞

⎟

⎠

⎛

⎜

⎝

0001

2001

2301

0301

1211

1111

⎞

⎟

⎠

⎛

⎜

⎝

−3000

0 −30 0

1501

000−3

⎞

⎟

⎠

⎛

⎜

⎝

000−3

−600−3

−6 −90−3

0 −90−3

−2 −10−2

−220−2

⎞

⎟

⎠

The images have Cartesian coordinates A



(0, 0, 0), B



(2, 0, 0), C



(2, 3, 0),



(0, 3, 0), E



(1, 0.5, 0), F



(1, −1, 0). The image of the prism is shown in Fig-

ure 4.8(b).

-1

Figure 4.8 Images of the prism after the application of (a) the parallel

projection of Example 4.6, and (b) the perspective projection of Example 4.7

EXERCISES

Determine the projection matrix M for the following.

4.6. Perspective projection onto the viewplane −x +3y +2z −4=0from

the viewpoint (2, −1, 1).

76 Applied Geometry for Computer Graphics and CAD

4.7. Perspective projection onto the viewplane 5x − 3z + 2 = 0 from the

viewpoint (1, 4, −1).

4.8. Parallel projection onto the viewplane 2y+3z+4 = 0 in the direction

of the vector (1, −2, 3).

4.9. Parallel projection onto the viewplane 7x−8y+5 = 0 in the direction

of the vector (0, 4, 9).

4.10. Let a tetrahedron have vertices A(0, 0, 0), B(1, 0, 0), C(0, 1, 0), and

D(1, 1, 1). Apply each of the projections of Exercises 4.6–4.9 to the

tetrahedron.

4.11. Implement the three-dimensional projection procedure with the fol-

lowing speciﬁcation. A viewpoint and viewplane are input by the

user, and the computed projection matrix is obtained as output. In

addition, the projected images of a number of input data points are

determined. Computer algebra packages have a procedure for mul-

tiplying matrices; but, if you are writing a computer program, then

you will need to devise your own algorithm to do this.

4.4 The Viewplane Coordinate Mapping

In the previous section three-dimensional projections were applied to give a

planar representation of a view of an object. At this stage of the viewing process

the view of the object is expressed in homogeneous three-dimensional world

coordinates. The next stage is to deﬁne a two-dimensional viewplane coordinate

system on the viewplane, and to represent the object view in terms of these

coordinates. The viewing pipeline will be completed by specifying a rectangular

viewplane window which identiﬁes the region of the viewplane to be viewed.

The viewplane window is mapped onto a rectangular device or viewport window

of the display device. Any part of the view lying inside the viewplane window

is mapped to the device window and displayed, but any part of the view lying

outside the rectangle is clipped, and does not appear as part of the displayed

image.

The viewplane (X, Y )-coordinate system is speciﬁed in terms of the world

coordinate system by an origin O(q

), and two unit vectors r =(r

)

and s =(s

) which indicate the directions of the X-andY -axes, respec-

tively. Consider a point on the viewplane with homogeneous world coordinates



(x, y, z, w), and homogeneous viewplane coordinates P



(X, Y, W ). The aim

is to obtain P



from P



by a mapping of the form P



= P



· VC,whereVC is

a4× 3 matrix. Rather than compute VC directly, the strategy is to determine