Martienssen W., Warlimont H. (Eds.). Handbook of Condensed Matter and Materials Data

Подождите немного. Документ загружается.

992 Part 5 Special Structures

Table 5.2-5 Reconstruction and relaxation of semiconductors, cont.

Crystal Face Reconstruction Preparation Model Remarks

symmetry

InAs (110) 1×1 Same as above Same as above

InSb (110) 1×1 Same as above Same as above

CdS (0001)Cd 1×1 IBA

CdSe (10

10) 1×1 Cleaving Rotation/relaxation Results controversial

(Fig. 5.2-17, Table 5.2-8)

ZnO (0001)Zn 1×1 Cleaving, IBA

placements of atoms that conserve the lengths of the

bonds but not their relative angles.

Figures 5.2-7 – 5.2-17 give the accepted recon-

struction models for a selection of covalent and

polar semiconductors, together with STM (scan-

ning tunneling microscopy) images of some of the

surfaces. Tables 5.2-6, 5.2-7, and 5.2-8 give the

positions of the atoms in reconstructed Si(111)

2 × 1 and Si (111)7 ×7 surfaces and the param-

eters of the rotation/relaxation model of polar

semiconductors.

<110>

1a 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

p(2× 2)

25 Å

1b 2 3 4 5 6 7 8 9 10 11 12 13 14 15

c(4× 2)

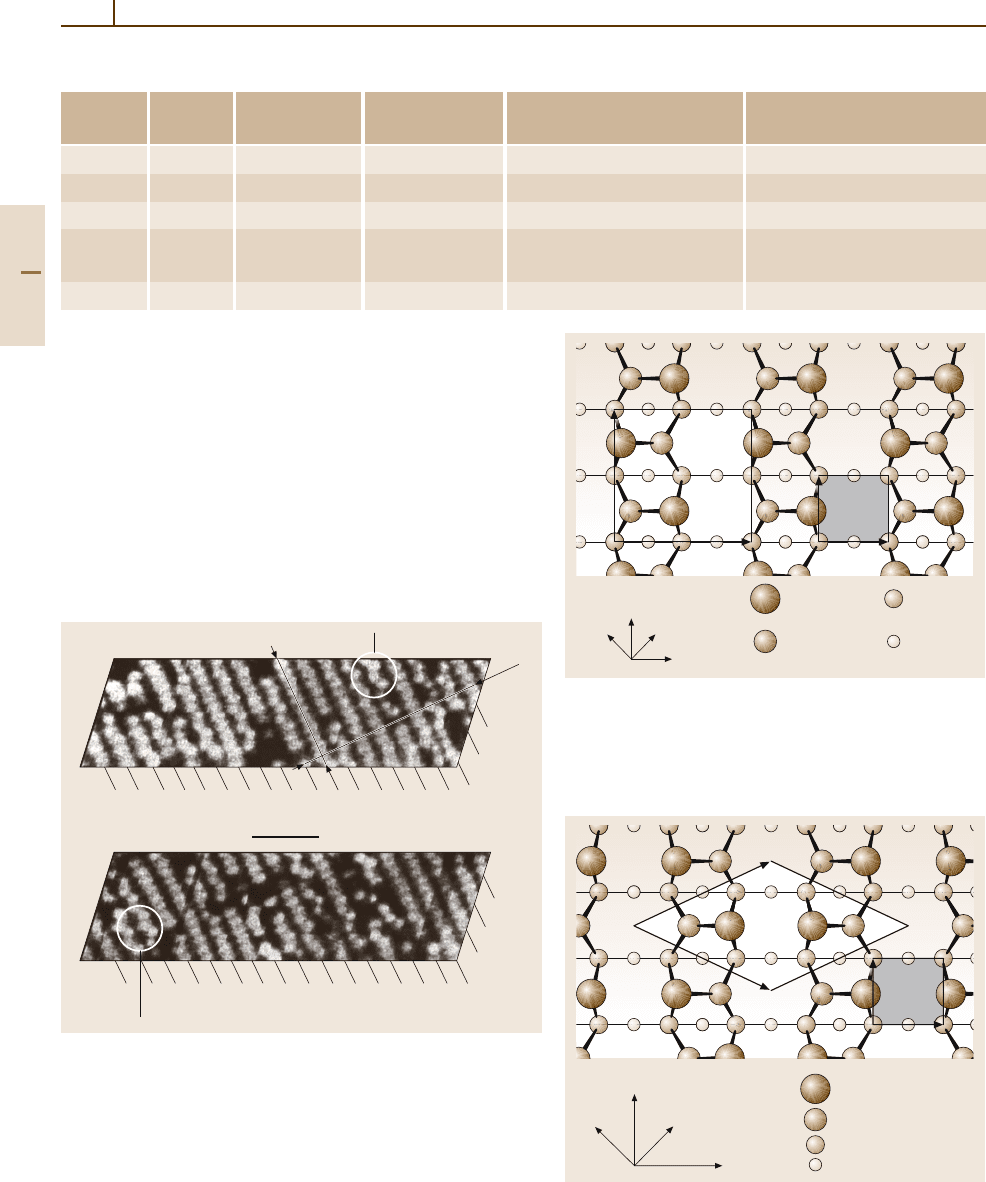
Fig. 5.2-9 STM image of the Si(100) surface showing coexistence

of 2 × 1, p(2× 2), and c(4× 2) reconstructions [2.20]

Fig. 5.2-10 Ordered arrangement of buckled dimers that

gives rise to c(4× 2) reconstruction of the (100) face of Si

and Ge (top views). Ideal (shaded) and reconstructed unit

cells are shown

1st layer,

upper atoms

1st layer,

lower atoms

2nd layer

3rd layer

[110]

[010][1

–

00]

–

10]

Fig. 5.2-8 Ordered arrangement of buckled dimers that

gives rise to p(2 ×2) reconstruction of the (100) face of

Si and Ge (top views). Ideal (shaded) and reconstructed

unit cells are shown

1st layer, upper atoms

[110]

[010][1

–

00]

–

10]

1st layer, lower atoms

2nd layer

3rd layer

Part 5 2.2

The Physics of Solid Surfaces 2.2 Surface Reconstruction and Relaxation 993

1st layer, upper atoms

1st layer, lower atoms

2nd layer

3rd layer

–

01]

–

10]

[01

–

11]

[111]

Table 5.2-6 Coordinates of the atoms of the uppermost

layers of Si(111) 2 ×1 (π-bonded chain geometry). The

atoms are labeled as in Fig. 5.2-11b. The origin is at atom 1;

the XYZ axes are in the directions [

1], [1

10], and [

12],

respectively

Atom X (Å) Y (Å) Z (Å)

1 0.0 0.0 0.0

2 0.34 1.92 1.12

3 1.32 0.0 −1.98

4 1.23 1.92 3.28

5 3.51 0.0 −1.14

6 3.40 1.92 2.35

7 4.09 0.0 1.16

8 4.35 1.92 −2.18

Data are average values from various authors.

References to the original papers are given in [2.3]

Fig. 5.2-11 (a) top view and (b) side view of the Pandey’s

π-bonded chain model for the 2 ×1 reconstruction of the

(111) face of diamond, Si and Ge [2.21]. In

(a) the ideal

(shaded) and 2×1 unit cells are shown. The numeration of

atoms in

(b) refers to the positions given in Table 5.2-6

10Å

2Å

[01

]

[21

]

Fig. 5.2-12 STM image of Si(111) 2×1, showing the great

anisotropy of the surface, in agreement with the model of

Fig. 5.2-11. Optical SDR spectra (see Fig. 5.2-41) show the

same anisotropy [2.22]

Part 5 2.2

994 Part 5 Special Structures

–

11]

–

01]

[01

–

11]

[111]

Si(111) 7 × 7

104

106

112

109

116

107

124

120105

119118117 119

126125

121

110

115

108

114

103

111

113

122 123

28 25

b) c)

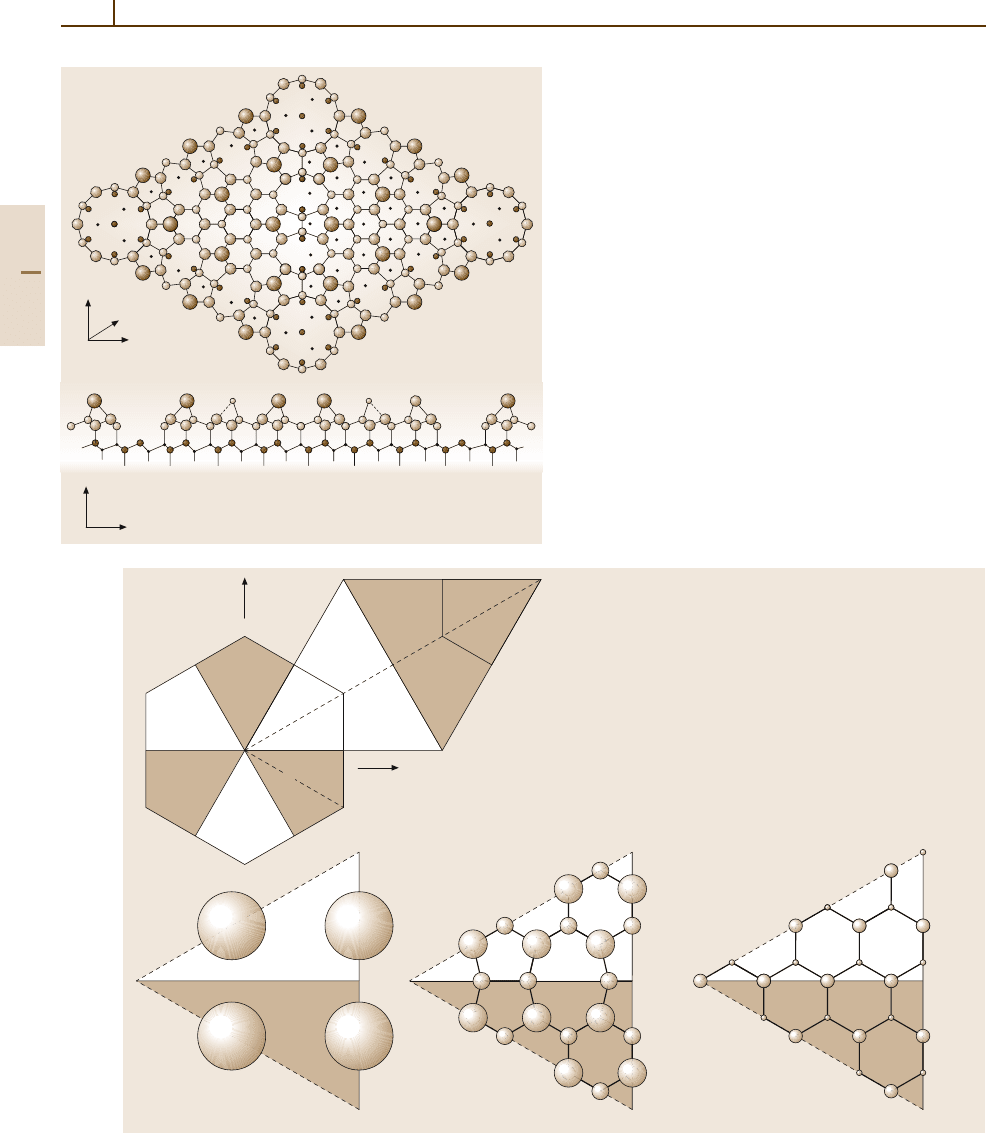
Fig. 5.2-13a,b DAS (dimers, adatoms, and stacking faults)

+ vacancy model of Takayanagi et al. for Si(111) 7 ×7.

(a) Top view; (b) side view. In (a), the unit cell could be

drawn by joining the centers of the four vacancies. The

faulted area is the triangular half-cell on the left. The rota-

tion associated with the stacking fault hides atoms in deep

unreconstructed layers, which, in contrast, are visible in the

unfaulted right-hand side [2.23]

Fig. 5.2-14a–d Symmetry-reduced unit cell for Si(111)

7×7(DASmodel).In

(a), the unit cell (two triangular

halves, one faulted (hatched) and one unfaulted) is reduced

to smaller subunits and recomposed into a c-hexagonal

cell. The atoms are drawn and numbered in

(b)–(d).The

numbering is the same as in Table 5.2-7; the origin of the

coordinates is at atom 103.

(b) The four adatoms; (c) the

ﬁrst- and second-layer atoms;

(d) the third- and fourth-layer

atoms [2.24,25]

Part 5 2.2

The Physics of Solid Surfaces 2.2 Surface Reconstruction and Relaxation 995

Table 5.2-7 Coordinates of the adatoms and four uppermost layer atoms in the symmetry-reduced unit cell of Si(111)

7× 7 (see Fig. 5.2-14 for the numbering of the atoms). The origin is taken at atom 103

.X-raydatagiveavalueof2.11 Å

for the adatom–back atom projected bond length (between atoms 1 and 13 and between atoms 1 and 28 in the table) and

a value of 2.49 Å for the dimer bond length (betweens atoms 26 and 27 in the table) [2.24–26]

Atom no. x (Å) y (Å) z (Å) Atom no. x (Å) y (Å) z (Å)

1 5.76 3.33 −4.21 103 0.00 0.00 −0.05

2 13.44 3.33 −4.17 104 13.44 7.76 0.73

3 5.76 −3.33 −4.29 105 5.76 3.33 0.45

4 13.44 −3.33 −4.25 106 13.44 3.33 0.45

13 4.01 2.32 −2.94 107 11.52 6.65 −0.07

14 5.76 3.33 −1.68 108 5.76 −3.33 0.45

15 9.60 5.54 −3.11 109 13.44 −3.33 0.45

16 11.55 6.67 −2.41 110 11.52 −6.65 −0.07

17 13.44 5.32 −2.98 111 1.92 1.11 0.74

18 13.44 3.33 −1.68 112 13.44 1.11 0.87

19 4.01 −2.32 −2.99 113 7.68 4.43 0.80

20 5.76 −3.33 −1.73 114 3.84 −2.22 0.85

21 9.60 −5.54 −3.16 115 9.60 −5.54 0.73

22 11.55 −6.67 −2.46 116 13.44 −5.54 0.80

23 13.44 −5.32 −3.03 117 3.84 0.00 0.00

24 13.44 −3.33 −1.73 118 7.68 0.00 0.00

25 12.21 0.00 −2.24 119 11.52 0.00 0.00

26 6.98 0.00 −2.24 120 9.60 3.33 −0.07

27 4.53 0.00 −2.24 121 9.60 −3.33 −0.07

28 7.49 2.33 −2.98 122 5.76 1.11 0.87

29 11.71 2.33 −2.98 123 9.60 1.11 0.72

30 9.60 3.29 −2.41 124 11.52 4.43 0.80

31 7.49 −2.33 −3.03 125 7.68 −2.22 0.83

32 11.71 −2.33 −3.03 126 11.52 −2.22 0.83

33 9.60 −3.29 −2.46

A table of the atomic positions for the full 7×7 cell is given in [2.25]. The results were obtained by LEED analysis [2.24]

Table 5.2-8 Surface relaxation and rotation parameters for polar semiconductors as deﬁned in Fig. 5.2-17

Crystal ω(

◦

) ∆

1⊥

(Å) ∆

2⊥

(Å) ∆

(Å) d

12⊥

(Å) d

12y

(Å) d

23⊥

(Å)

GaAs 27.4 0.65 −0.12 4.39 1.43 3.31 2.06

GaP 27.5 0.63 0.0 4.24 1.44 3.20 1.93

GaSb 30 0.77 0.0 4.79 1.61 3.27 2.16

InAs 36.5 0.78 −0.15 4.98 1.50 3.60 2.21

InP 28 0.69 0.0 4.57 1.59 3.45 2.07

InSb 28.8 0.78 −0.18 5.06 1.60 3.82 2.38

CdSe 21.3 1.03 0.0 4.60 0.45 4.10 2.48

The data were obtained by dynamical LEED analysis. References to the original papers are given in [2.3,4]

Part 5 2.2

996 Part 5 Special Structures

Si(111) 7 × 7

112

–

∆

2, ⊥

∆

1, y

∆

1, ⊥

12, ⊥

12, y

23, y

23, ⊥

Cation

Anion

Side view

Fig. 5.2-17 Side view of the relaxed cell of a GaAs-type

crystal, with parameters occurring in the relaxation/rotation

model of the (110) face used in Table 5.2-8

Fig. 5.2-15 STM image of the Si(111)7 × 7 surface. The

picture gives evidence to the 12 adatoms, the 4 vacancies,

and the asymmetry between the two triangular half cells of

Fig. 5.2-13 [2.7,27]

Ge(111) c(2 × 8)

[11

–

[101

–

][011

–

]

[112

–

]

Fig. 5.2-16 Top view of Ge(111)c(2 × 8) simple adatom

model. Large and small empty circles represent adatoms

and “rest” atoms respectively. Both ideal (shaded)and

c(2× 8) unit cells are shown [2.28]

5.2.3 Electronic Structure of Surfaces

The truncation of the lattice and/or the reconstruction

and relaxation cause the electronic states at the surface

or in the uppermost layers to be distinctly different from

those of the bulk. Such new states are called surface

states. Their wave functions decay exponentially on both

sides of the surface. Since their k

⊥

is imaginary, the sur-

face band structure is deﬁned in the surface Brillouin

zone (SBZ), which is the projection of the 3-D Brillouin

zone onto the surface plane. The projection of the bulk

bands onto the SBZ is called the projected band struc-

ture. When the energy of a surface state is localized in

a gap of the projected bulk structure (either an absolute

gapp, i. e. one that extends throughout the whole SBZ,

or a partial gap), one speaks of a true (or bona ﬁde)

surface state. When there is degeneracy (both in energy

and k) with the bulk bands, one speaks of a surface

resonance.

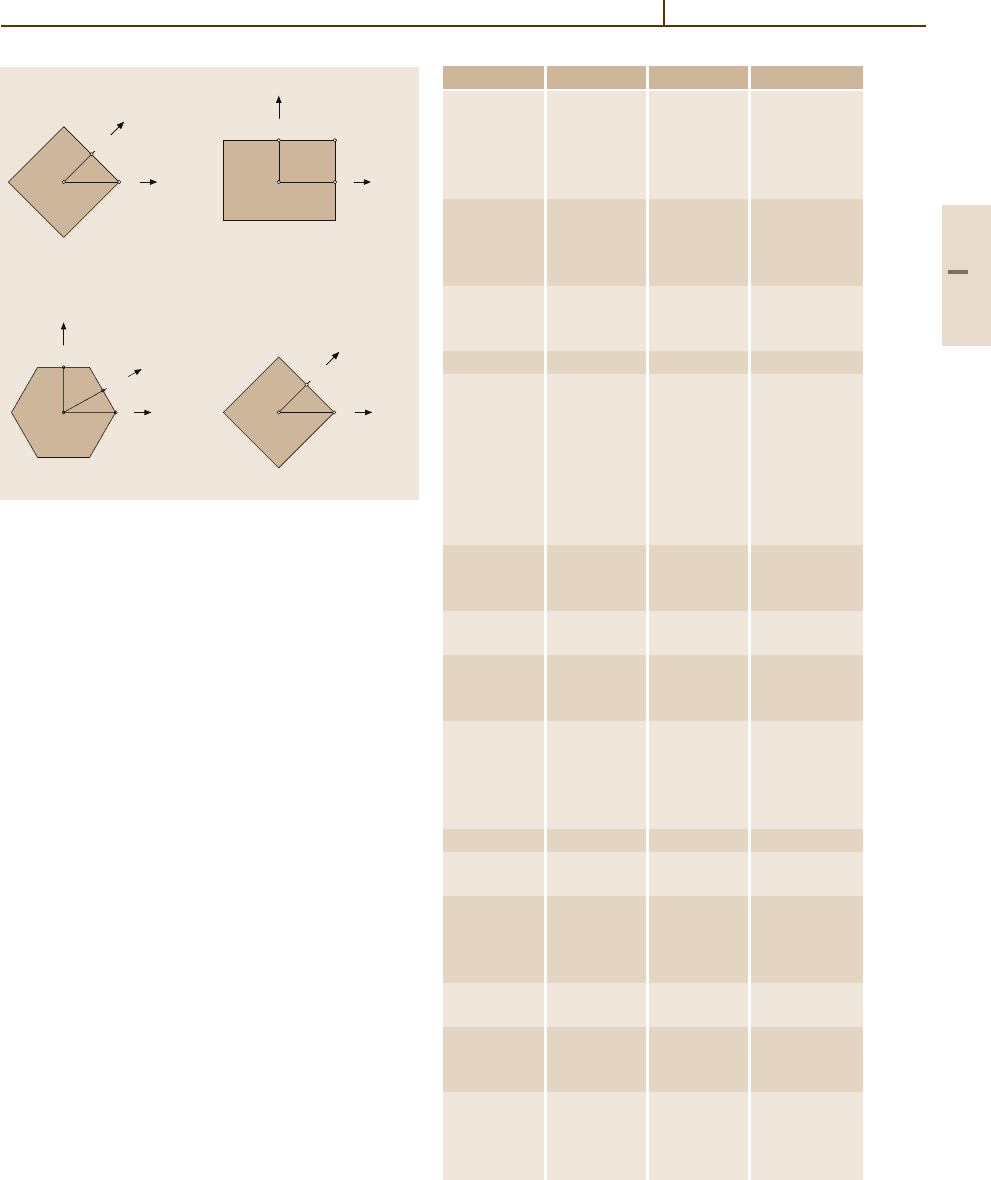
The SBZs, of the most common faces of fcc and bcc

crystals are shown in Fig. 5.2-18.

The potential felt by an electron outside the surface

(though sufﬁciently far from it) is the classical image

potential: (−e

/4z)(ε −1)/(ε +1), ε being the dielec-

tric function of the crystal. From a microscopic point of

view, the image potential arises from the charge density

ﬂuctuations induced in the solid by the outside electron.

An important consequence of the Coulomb-like image

potential is the occurrence ofimage states in the potential

well outside the solid (especially in metals). In surface

structure calculations done with the local-density ap-

proximation (LDA), such image states are not present,

Part 5 2.3

The Physics of Solid Surfaces 2.3 Electronic Structure of Surfaces 997

[21

–

]

[011

–

]

[12

–

[011]

[001

–

––

–

––

–

––

[001]

–

10]

fcc (100) fcc (110)

fcc and bcc (111) bcc (100)

––

–

[010]

[011]M

––

–

Fig. 5.2-18 Surface Brillouin zones of fcc (100), (110), and

(111), bcc (100) and (111) faces

since the potential decays exponentially on the vacuum

side. Nonlocal forms of the exchange correlation ener-

gies that give the correct long-range potential have been

introduced to overcome this difﬁculty.

Surface states were ﬁrst detected by optical tech-

niques in semiconductors and are now studied mainly

by ARUPS, KRIPES, STM, SDR, and reﬂectance

anisotropy spectroscopy (RAS).

Data, in the form of tables and ﬁgures, are presented

separately for metals (including jellium), semiconduc-

tors, and magnetic surfaces.

5.2.3.1 Metals

The data are ordered alphabetically according to the

chemical symbol. Where necessary, introductory re-

marks are given. A more detailed discussion is given

in [2.9,11].

Work Function Data

Work function data are listed in Table 5.2-9 with the

speciﬁcation of the method of measurement.

Table 5.2-9 Work functions Φ of metals (average values

from various authors; references to the original papers are

given in [2.9, 16]). P, photoelectric threshold; A, angle-

resolved photoemission spectroscopy; T, thermionic emis-

sion; F, ﬁeld emission; th, theory

Metal Face Φ(eV) Technique

(100) 4.18 P

4.38 A

4.2 th

(111) 4.46 P

4.50 A

(100) 4.30 P

(110) 4.17 P

(111) 4.23 P

4.5 th

(100) 5.22 A

(110) 5.20 A

(111) 5.26 A

Co (0001) 5.2 A

(100) 4.59 P

4.63 A

5.10 F

4.5 th

(110) 4.48 P

4.5 A

(111) 4.85 P

4.5 A

(100) 4.67 P

(110) 5.05 A

(111) 4.81 P

(110) 5.42 F

(111) 5.76 F

(100) 4.53 P

(110) 4.95 P

(111) 4.55 P

(100) 4.89 T

5.53 F

5.1 th

(110) 4.64 T

(111) 5.22 T

Pb (111) 4.05 A

(111) 5.58 A

5.8 th

(100) 5.84 P

5.84 F

(111) 5.82 A

5.93 F

(100) 5.1 th

(111) 5.35 th

(100) 4.15 T

(110) 4.80 T

(111) 4.00 T

(100) 4.66 F

4.5 th

(110) 5.57 F

(111) 4.46 F

Part 5 2.3

998 Part 5 Special Structures

Surface Core Level Shifts (SCLS)

A shift in the energy of the core levels is caused by

charge transfer between surface and bulk atoms. A posi-

tive SCLS means a larger binding energy. It is generally

assumed that in metals the change in the width of the

band and its position with respect to the Fermi energy are

the important factors. Data are shown in Table 5.2-10.

Jellium Model

The jellium model of a metal surface takes into account,

in a simpliﬁed though signiﬁcant way, the problem of

electron–electron interaction. The atomic potential is

smeared out into a uniform positive background extend-

ing over the region z ≤ 0. The electron density is taken

into account by a dimensionless parameter r

,deﬁned

by the equation

(4/3)π(r

)

n =1 ,

where a

is the Bohr radius and n the bulk electron

density.

Figure 5.2-19 shows the charge density as a function

of z for r

= 2 and r

= 5, corresponding roughly to

Al and K. Table 5.2-11 gives the values of the work

function Φ for various values of r

and compares the

Table 5.2-10 Surface core level shift data. The data are from various authors. References to the original papers are given

in [2.9]

Metal Surface Core level SCLS (eV) Remarks

(100)

−0.057 Photoemission (partial yield)

−0.120 Theory

(110) and (111) 0.0 UPS

(100) 1× 1

−0.35 UPS

(100) 5×20 −0.28 UPS

(111) −0.35 UPS, no distinct results for (111) 23 × 1

(100) 3s −0.36 Theory

2p −0.27 UPS

(100) 1× 5

−0.49

(111) −0.50

(110) 1× 2

−0.21 UPS, evidence for nonequivalent atoms

−0.55

(111) −0.40 UPS

(100)

−0.75 1st layer Theory

−0.05 2nd layer

(111) −0.46 1st layer

−0.05 2nd layer

(110)

−0.30 UPS

−0.30 1st layer Theory

−0.02 2nd layer

n/n

z (2π/k

)

1.0

1.00

0.75

0.50

0.25

– 1.0 – 0.5 0 0.5

= 5

= 2

Positive

background

Fig. 5.2-19 Charge density near a jellium surface, for

= 2andr

= 5 as a function of z [2.29]

Part 5 2.3

The Physics of Solid Surfaces 2.3 Electronic Structure of Surfaces 999

Table 5.2-11 Work functions for the jellium model. Refer-

ences to the original papers are given in [2.9]

jellium

(eV ) Element Φ

exp

(eV )

2 3.89 Al (r

= 2.08) 4.25

2.5 3.72

3 3.50 Ag (r

= 3.02) 4.35

3.5 3.26

4 3.06 Na (r

= 3.93) 2.45

4.5 2.87

5 2.73 K(r

= 4.86) 2.3

results with experimental values for metallic elements

of comparable densities. Figure 5.2-20givessome useful

insight into the problem of the potential near a metallic

surface.

Image States

Image states are conﬁned to the region of space between

the crystal surface and the image potential which de-

scribes the electrostatic force acting on an electron close

to the surface. Figure 5.2-21 illustrates the occurrence

of image states in Ag(100). The ﬁgure shows (i) the

electron potential inside and outside the crystal, (ii) the

image state levels n = 1 and n = 2 and the correspond-

ing wave functions, and (iii) the bulk band structure

E (arb. units)

z (2π/k

)

– 1.0

1.0

0.12

0.08

0.04

– 0.04

– 0.08

– 0.5 0 0.5

= 5

eff

Fig. 5.2-20 Effective one-electron potential V

eff

(contin-

uous line) and its electrostatic part (dashed line) near

a jellium surface for r

= 5. Notice the characteristic os-

cillations (Friedel oscillations) [2.29]

vac

= 0

0.4

0.3

0.2

0.1

10 15 20 25 30

z (Å)

ΓX

–12

2∆

∆

Potential

VacuumΨ

n = 1

n = 2

n = 1

= – 0.81 eV

n = 2

= – 0.19 eV

Interplanar spacing

Bulk

Ag(100)

Fig. 5.2-21 Schematic drawing of energy versus distance at the sur-

face of Ag(100), illustrating the origin of the image states. Wave

functions for n = 1andn = 2 are also displayed in the right part

of the ﬁgure, corresponding to the levels in the potential well. On

the left side of the ﬁgure the bulk energy bands as a function of k

are also shown. Notice that the image state energies occur in the

band gap of the bulk. This allows conﬁnement of the image state

electron [2.30, 31]

with an energy gap of width 2∆. It can be seen that

the image state levels have energies corresponding to

the bulk gap so that the electron cannot penetrate the

crystal [2.32].

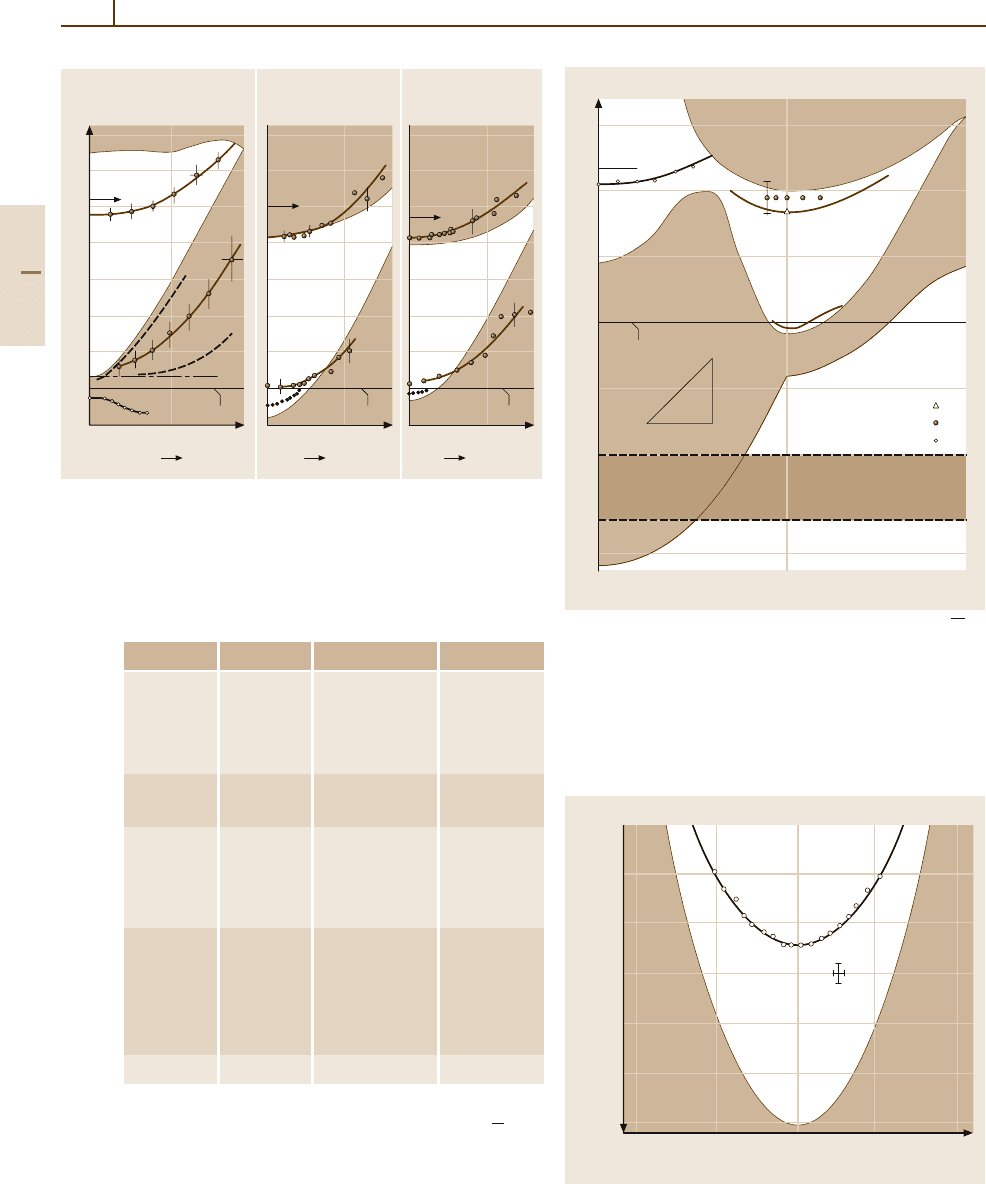
Figure 5.2-22 shows the dispersion curves E(k



)

for the (111) faces of Ni, Cu, and Ag. Image states

) and surface and resonance states (S

),to-

gether with the projected bulk bands (hatched regions),

are shown. Table 5.2-12 gives average values of the

binding energies E

(measured downward from the vac-

uum level) and effective masses m

∗

for some image

states.

Surface Dispersion Curves E(k



)

Dispersion curves are given as a function of k



along

symmetry lines of the SBZ in Figs. 5.2-23 – 5.2-30.

Where possible, a comparison with theoretical results

and the projected bulkband structure has been presented.

Most of the experimental data were obtained by

ARUPS (for ﬁlled states) and KRIPES (for empty

states). Since the component k



is conserved across the

Part 5 2.3

1000 Part 5 Special Structures

E (eV)

0.5

–1

1.00 0.5 0.500

(Å

–1

)

–

(Å

–1

)(Å

–1

)

–

k M

––

⎮⎮

vac

Ni(111) Cu(111) Ag(111)

Fig. 5.2-22 Dispersion curves E(k



) for the empty states of the

(111) face of Ni, Cu and Ag, showing image states (S

), surface

states and resonances (S

). Experimental data by KRIPES [2.33]

Table 5.2-12 Image state parameters. The data are from

various authors. References to the original papers are given

in [2.9]

Crystal Face E

(eV ) m

∗

(100) 0.51 1.32

0.16 (n = 2)

(111) 0.69 1.35

0.23 (n = 2)

(100) 0.63 1.0

(111) 0.42

(100) 0.65 1.13

0.18 (n = 2)

(110) 0.48

(111) 0.82 1.07

(100) 0.4 1.2

(110) 0.6 1.7

(111) 0.74 1.3

0.25 (n = 2)

0.10 (n = 3)

Pt (111) 0.63

Fig. 5.2-25 Energydispersion curves E(k



) around Γ point

of the SBZ for Ag(111). Experimental data from ARUPS

are ﬁtted with a parabolic band with m

∗

= 0.53 [2.36]

E (eV)

–

––

––

–2

–4

–6

d band

–

––

––

Ag(100)

vac

Fig. 5.2-24 Energy dispersion curves E(k



) around Xof

the SBZ for Ag(100). Projected bands and surface state fea-

tures A and B are the same as in Fig. 5.2-8a. Experimental

points are obtained by: electroreﬂectance (1) and KRIPES

(2 and 3). Curve (3) represents image states [2.34,35]

= 0

– 0.2

0.05

0.10

0.15

0.20

0.25

0.30

(eV)

– 0.1 0 0.1 0.2

⎮⎮

(Å

–1

)

–

SS Ag(111)

Part 5 2.3

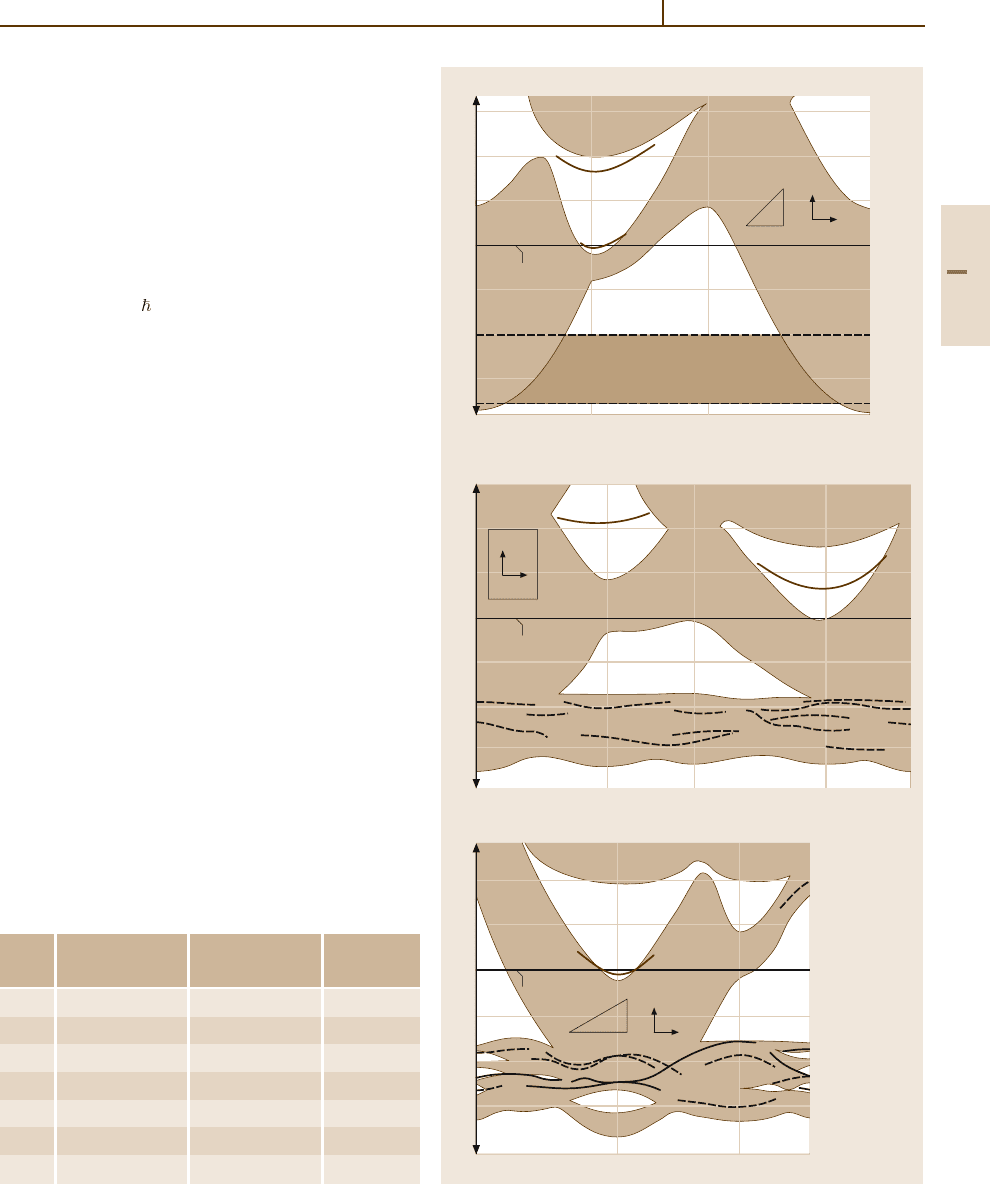
The Physics of Solid Surfaces 2.3 Electronic Structure of Surfaces 1001

Fig. 5.2-23 Theoretical projected band structures (shaded

areas) along symmetry lines of the SBZ for Ag(100),

Ag(110) and Ag(111). Surface states (solid lines)and

resonances (dashed lines) are shown. SBZ in the in-

sets [2.37–39]

surface, the determination of the direction of the emitted

or incident electron in ARUPS or KRIPES, respectively,

and its energy allows the determination of the dispersion

curve through the relation



= (2mE

kin

)

1/2

sin θ,

where E

kin

is the kinetic energy of theemitted or incident

electron and θ the angle of emission or incidence with

respect to the surface normal.

Because of the large amount of data available for

metals, only a few signiﬁcant examples have been given.

For more detailed information, the reader is referred

to [2.9, 11].

Surface Plasmons

Surface plasmons are self-sustained oscillations that de-

cay exponentially on both sides of the surface plane.

They occur at the poles of the loss function, i. e. for

= 0inthebulkandε

=−1 at the surface, ε

be-

ing the real part of the dielectric function. The surface

plasmon is shifted to lower energies with respect to the

bulk.

Table 5.2-13 gives some of the parameters of surface

plasmons for various metals. d

⊥

(ω) is, in the jellium

model, the distance of the centroid of the induced charge

from the surface plane. d

⊥

> 0 means that the centroid

is outside the edge of the jellium. Figure 5.2-31 shows

the dispersion curves of surface plasmons for Al(111).

For a more detailed discussion see [2.12].

Table 5.2-13 Surface plasmon parameters. The data are

from various authors. References to the original papers are

given in [2.12]

Metal Surface plasmon Bulk plasmon d

⊥

(ω

) (Å)

energy (eV) energy (eV )

Al 10.3 15

Mg 7.38 10.4 0.82

Li 4.3 7.12 0.48

Na 3.98 5.72 0.73

K 2.73 3.72 0.73

Rb 3.41

Cs 1.99 2.90 0.88

E (eV)

–2

–4

–6

–

––

–

––

E (eV)

–2

–4

–6

––

–

––

E (eV)

–2

–4

–6

–8

––

–

––

––

d-band

Ag(100)

011

–

––

––

Ag(110)

–

001

–

––

––

––

Ag(111)

–

––

Part 5 2.3