Martienssen W., Warlimont H. (Eds.). Handbook of Condensed Matter and Materials Data

Подождите немного. Документ загружается.

1012 Part 5 Special Structures

5.2.4 Surface Phonons

The lattice dynamics is strongly perturbed by the pres-

ence of the surface. The elements of the force constant

matrix connecting two atoms at or near the surface dif-

fer from those for the bulk. The number of neighbors is

also different at the surface. Vibrational frequencies are

generally expected to be lower than in the bulk.

Phonon bands occur in the SBZ, similarly to the sur-

face states discussed in Sect. 5.2.3. When the frequency

of a surface mode corresponds to a gap in the bulk spec-

trum, the mode is localized at the surface and is called

a surface phonon. If degeneracy with bulk modes ex-

ists, one speaks of surface resonances. Surface phonon

modes are labeled S

( j = 1, 2, 3,...), and surface res-

onances by R

; when strong mixing with bulk modes is

present, the phonon is labeled MS

. The lowest mode

that is desired from the (bulk) acoustic band is often

called the Rayleigh mode, after Lord Rayleigh, who

ﬁrst predicted (in 1887) the existence of surface modes

at lower frequencies than in the bulk.

0.5

100

3.0

0 0 0.2 0.4 0.6 0.8 1.0

–

––

–

(cm

–1

)

[ξξ][ξ 0]

00 10

ξξ

2.5

2.0

1.5

1.0

0.5

ν (THz)

Ag(001)

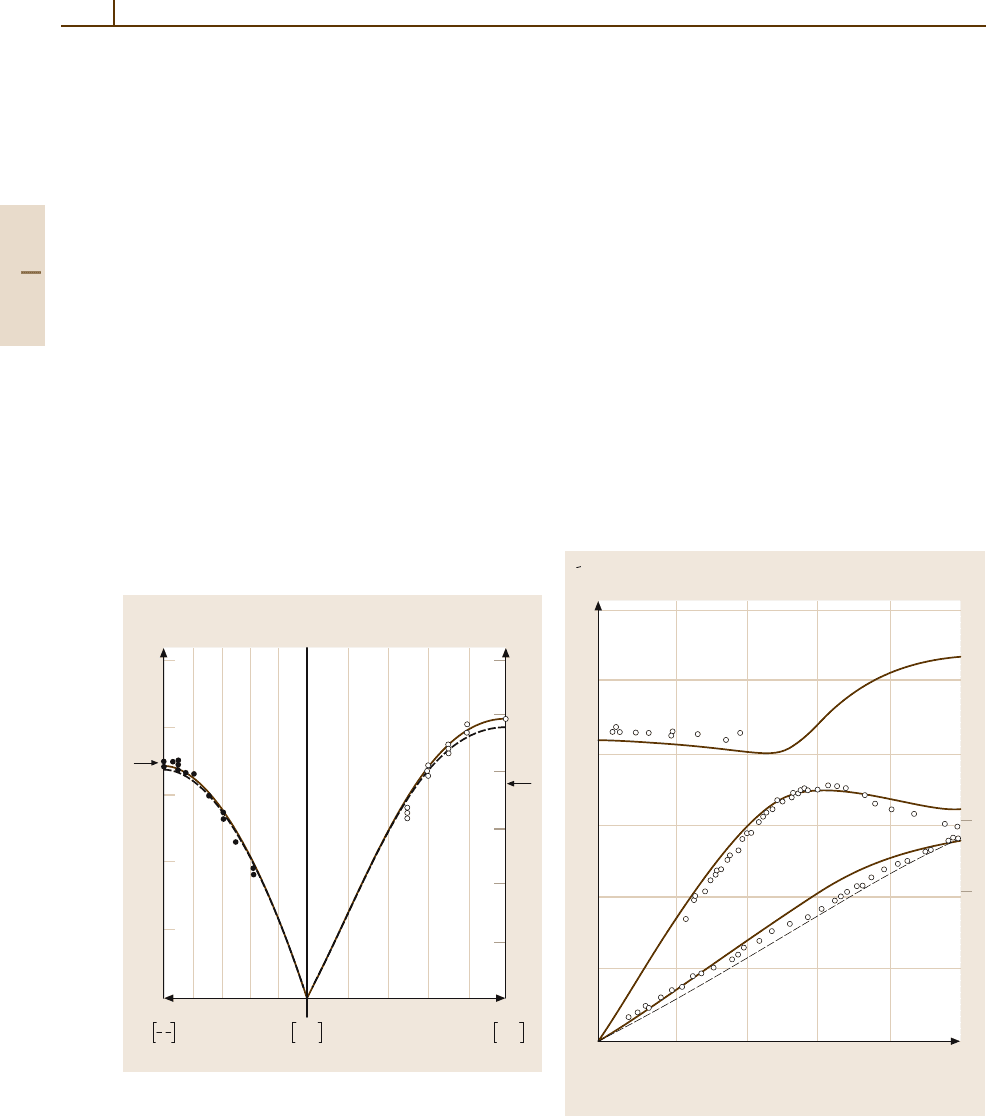
Fig. 5.2-49 Surface phonon dispersion curves for Ag(100)

measured by EELS. The ﬁlled and open circles re-

fer to different electron energies. The full and dashed

lines are theoretical ﬁts. Energies are given in cm

−1

1cm

−1

= 0.1240 meV [2.80]

The experimental results have been obtained mainly

through atom and electron scattering, HATOF and

EELS.

5.2.4.1 Metals

Surface phonon bands along symmetry lines of the SBZ

are given for fcc metals in Figs. 5.2-49 – 5.2-55 and in

Table 5.2-20. In all ﬁgures the horizontal axis is the

reduced wave vector, expressed as the ratio to its value

at the zone boundary. Table 5.2-21 gives the surface

Debye temperatures for some fcc and bcc metals, as well

as the amplitudes of thermal vibrations of atoms in the

ﬁrst layer: ρ

as compared with those of the bulk: ρ

In the harmonic approximation, the root mean square

displacement of the atoms is proportional to the inverse

of the Debye temperature.

[10]

1.0

[00]

0.2

0.4 0.6 0.8

hω (meV)

–

––

[ξ 0]

Ag(110)

Fig. 5.2-50 Surface phonon dispersion curves for Ag(110)

measured by HATOF. The solid curves are theoretical ﬁts

[2.81]

Part 5 2.4

The Physics of Solid Surfaces 2.4 Surface Phonons 1013

Table 5.2-20 Surface phonon energies of fcc metals. References to the original articles are given in the ﬁgure captions and/or

in [2.14,15]

Metal Face Energy (meV) and mode Figure Technique

(100) 10.2 (M) 8.6 (X) Fig. 5.2-49 EELS

(110) 8.15 (X) Fig. 5.2-50 HATOF

5.0 (Y) 7.7 (Y)

(111) 8.7 (M) Fig. 5.2-51 HATOF

9.1 (K)

(100) 15.1 (X) EELS

(110) 14.6 (X) Fig. 5.2-52 HATOF

8.9 (Y) 13.5 (Y)

(111) 17 (M) HATOF

18.6 (K)

(110) 2 × 1 Fig. 5.2-53 EELS

(111) 7.5 (M) HATOF

7.5 (K)

(100) 16.7 (M) 20.2 (M) Fig. 5.2-54 EELS

14.1 (X) 13.6 (X)

(110)

∼

14 (

X) 13 (Y) HATOF

7.5 (Y)

(111) 13.3 (M) 26.1 (M) EELS, HATOF

14.0 (K)

(100) 19.2 (M) 16.1 (X) Fig. 5.2-55 EELS, HATOF

(110) 17 (X) 15.8 EELS

9.9 (Y)

(111) 17.2 (M) 32.2 (M) EELS

Pd (110) 11 (X) HATOF

6.7 (Y) 9 (Y)

Pt (111) 10.8 (M) HATOF

11.1 (K)

Table 5.2-21 Surface Debye temperatures of metals. References to the original articles are given in [2.4,6]

Crystal Bulk Θ

(K) Face Surface Θ

(K) ρ

/ρ

Technique

Ag 225

(100) 104 LEED

(110) 150–190 LEED

1.5 LEIS

1.65 MEIS

1.44 HEIS

(111) ⊥ surface 155 LEED

 surface 226

247 HAS

Al 428

(100) 200 LEED

1.25 HEIS

(110) 140 LEED

(111) 200 LEED

Part 5 2.4

1014 Part 5 Special Structures

Table 5.2-21 Surface Debye temperatures of metals, cont.

Crystal Bulk Θ

(K) Face Surface Θ

(K) ρ

/ρ

Technique

Au 165

(100) 82 LEED

(110) 2 × 1 83 LEED

127 LEIS

1.55 HEIS

(111) 83 LEED

Cu 343

(100) 230 LEED

260 LEIS

1.5 MEIS

(110) 260 (150) 1.5 LEIS

1.55 MEIS

1.27 HEIS

(111) 245 LEED

Fe 467 (111) 1.18 MEIS

Ir 420

(110) 150 LEED

160 LEIS

(111) 170 LEED

Mo 450 (100) 239 LEED

Ni 450

(100) 1.46 MEIS

1.35 HEIS

(110) ⊥ surface 216 LEED

 surface 344

395 MEIS

1.15 HEIS

(111) ⊥ surface 208 LEED

 surface 348

1.20 HEIS

Pt 240

(100) 118 LEED

(110) 107 LEED

1.6 MEIS

(111) 111 LEED

1.3 MEIS

Rh 480 (111) 197 LEED

V 380 (100) 250 LEED

W 400

(100) 1 × 1 210 LEED

(100) c2 × 2 400 (200) LEED

1.5 HEIS

(110) 190–235 LEED

2.6, 1 HEIS

Part 5 2.4

The Physics of Solid Surfaces 2.4 Surface Phonons 1015

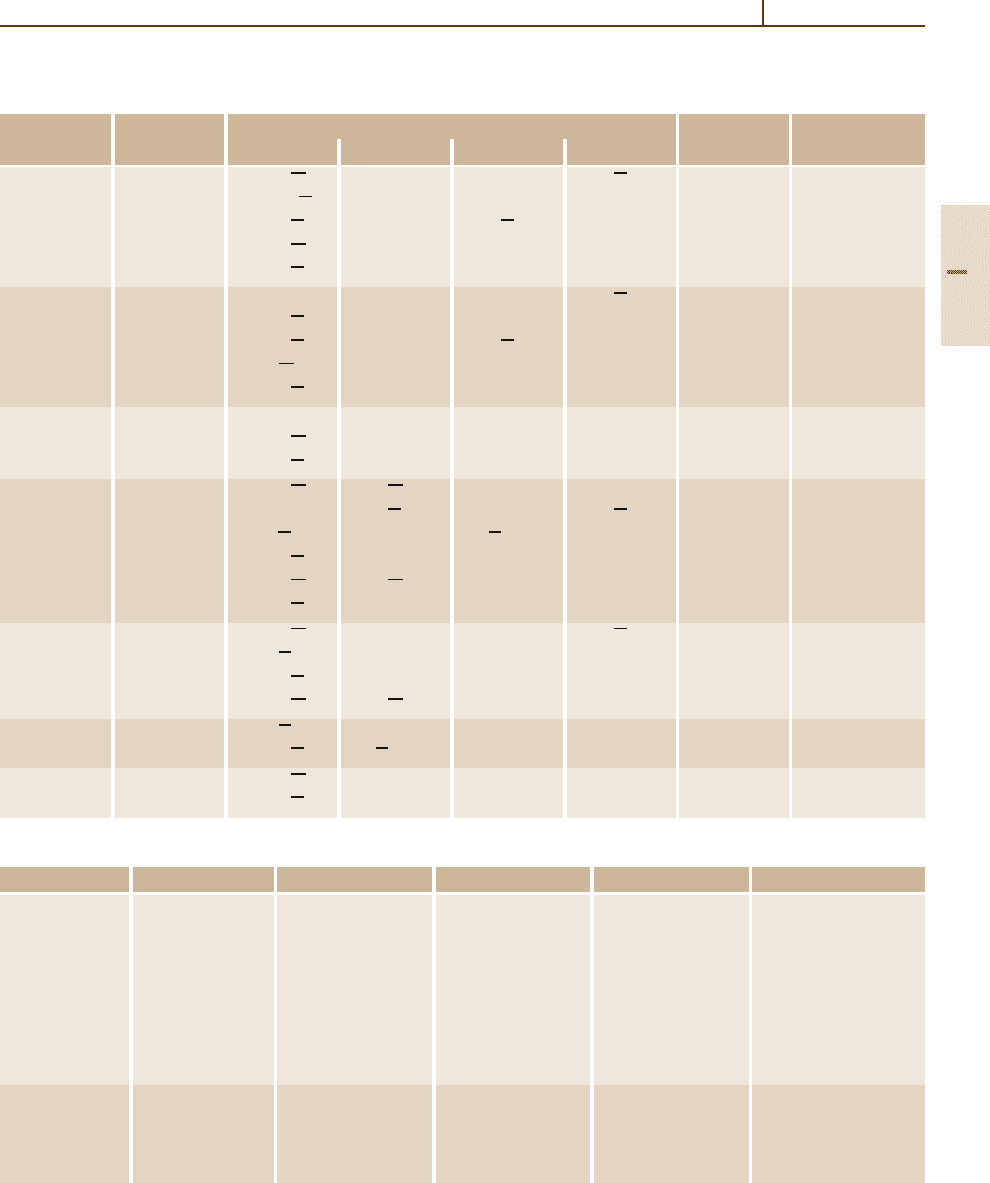
Fig. 5.2-51 Surface phonon dispersion curves for Ag(111)

measured by HATOF. Cirles are experimental points; solid

and dashed lines theoretical calculations. The hatched area

represents the projected band structure [2.82].

Very similar plots hold for Au(111) and Cu(111). For

appropriate energy parameters see Table 5.2-20

1.0

175

5.0

–

(cm

–1

) ν (THz)

––

150

125

100

4.5

4.0

3.5

3.0

2.5

2.0

1.5

1.0

0.5

[0 1]

[1 0][0 0]

ξξ

[0 ξ][ξ 0]

–

––

–

––

[001] [11

Au (110) 1 × 2

––

–

Fig. 5.2-53 Surface phonon dispersion curves along two

directions of the SBZ for reconstructed Au(110) 2 × 1,

measured by EELS. The dashed lines are theoretical re-

sults. In the inset, the SBZ shows the folding due to the 2 ×1

reconstruction that introduces the optical bands. Energies

aregivenincm

−1

.1cm

−1

= 0.1240 meV [2.84]

ω (10

rad/s)

hω (meV)

3.5

3.0

2.5

2.0

1.5

1.0

0.5

001.0 0 0.5 1.0 1.0

00 10

ξξ

–

––

–

Ag(111)

–

[ξ 0]

hω (meV) h ω (meV)

[0 ξ]

0 0.2 0.4 0.6 0.8 1.0 1.0 0.8 0.6 0.4 0.2 0

––

–

[0 0] [0 0][1 0] [0 1]

ξξ

Al (110) Al (110)

Fig. 5.2-52 Surface phonon dispersion curves for Al(110). The ex-

perimental results (circles) were obtained by HATOF. The solid and

dashed lines are theoretical ﬁts. The shaded regions represent the

projected bulk modes [2.83]

Part 5 2.4

1016 Part 5 Special Structures

0.4

1.0

320

280

240

200

160

120

0.5 0.4 0.3 0.2 0.1 0 0 0.2 0.6 0.8

–

––

ν (THz)ν

–

(cm

–1

)

ξξ

Ni (001)

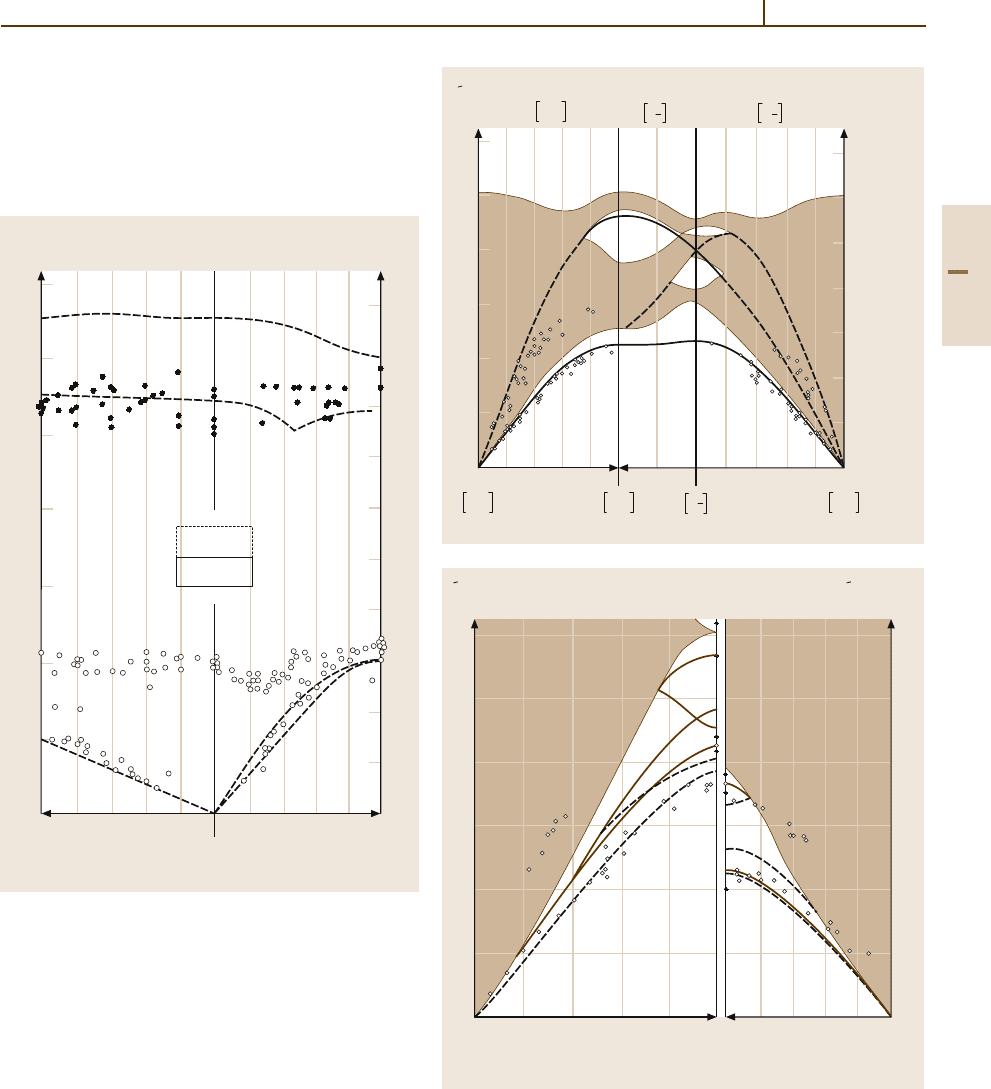
Fig. 5.2-55 Surface phonon dispersion curves of Ni(100) obtained

by EELS. S

, surface phonons; R

, surface resonances. Energies are

givenincm

−1

.1cm

−1

= 0.1240 meV [2.86]

0.5

1.0

140

120

100

4.0

3.5

3.0

2.5

2.0

1.5

1.0

0.5

ξξ

–

––

ν (THz)ν

–

(cm

–1

)

ξξ

Cu (001)

Fig. 5.2-54 Surface phonon dispersion curves for Cu(100)

measured by EELS. The solid and dashed lines

are theoretical ﬁts. Energies are given in cm

−1

1cm

−1

= 0.1240 meV [2.85]

Part 5 2.4

The Physics of Solid Surfaces 2.4 Surface Phonons 1017

5.2.4.2 Semiconductors and Insulators

Phonon surface bands of some insulators and semi-

conductors are given in Figs. 5.2-56 – 5.2-58. Surface

phonon energies of alkali halide crytals are summarized

in Table 5.2-23. Since insulators and semiconductors

have in general more than one atom per unit cell, they

display both acoustical and optical branches. Surface

Debye temperatures of some semiconductors are given

in Table 5.2-22.

1.0 1.0

–

––

–

[0 1] [1 1][0 0]

[0 ξ][ξξ]

hω (meV)

GaAs (110)

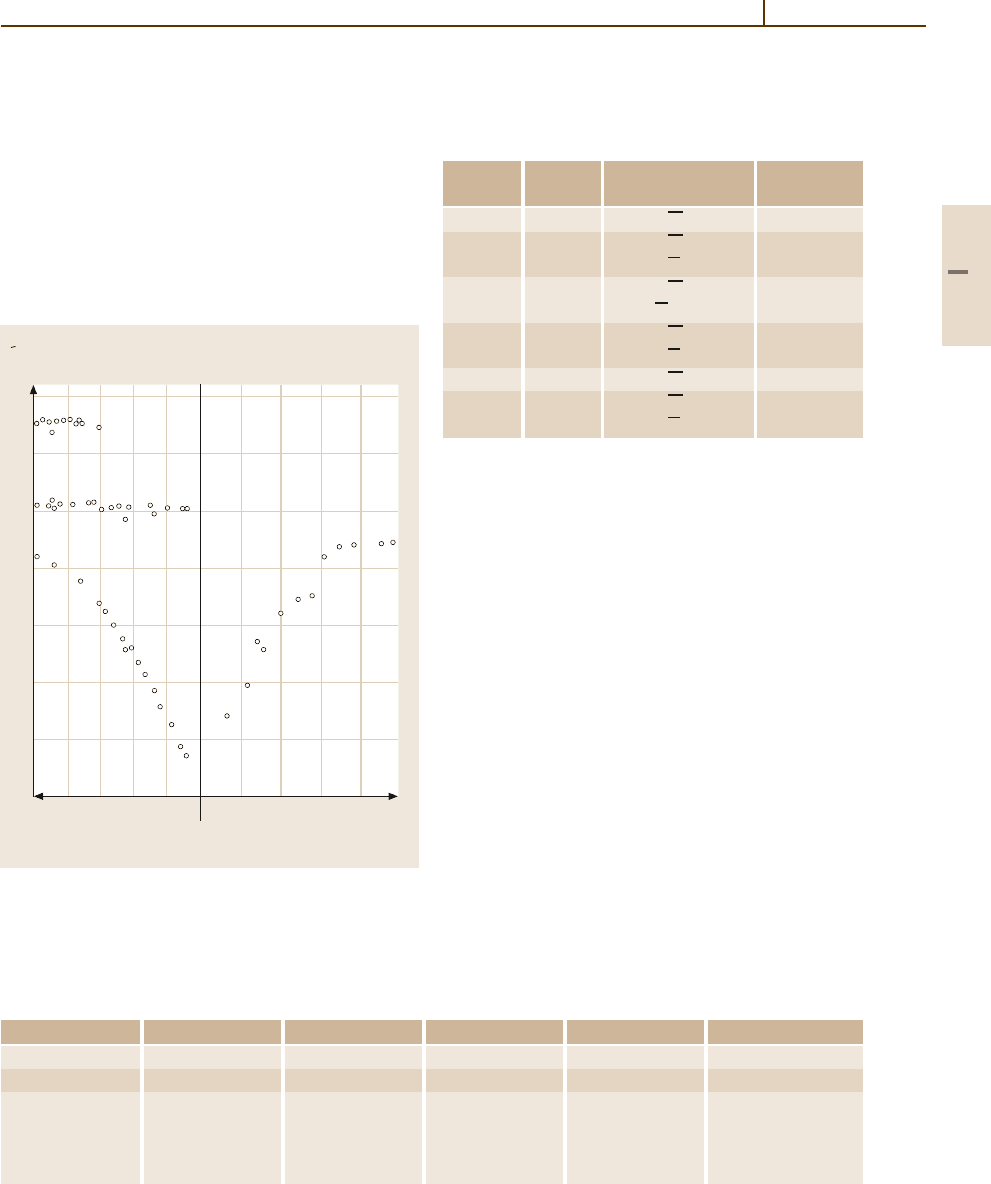
Fig. 5.2-56 Surface phonon dispersion curves for

GaAs(110) measured by HATOF (open circles). The en-

ergies at symmetry points are: Y, 8.3, 10.2, and 13.0meV;

Γ,10.0meV;S,8.9 meV [2.87]

Table 5.2-22 Surface Debye temperatures of semiconductors. References to the original articles are given in [2.4, 6]

Crystal Bulk Θ

(K) Face Surface Θ

(K) ρ

/ρ

Technique

GaSb 265 (110) 1.57 MEIS

InAs 249 (110) 1.65 MEIS

Si 640

(100) 430–475 HEED

1.4 HEED, LEED

(111) 2 × 1 1.45, 2.1 MEIS

300 HEIS

Table 5.2-23 Surface phonon energies of alkali halides.

References to the original articles are given in [2.14, 15]

Crystal Face Energy of mode S

Technique

(meV)

LiF (100) 22.9 (M) HATOF

NaF (100) 16.0 (M) HATOF

18.5 (X)

NaCl (100) 9.9 (M) HATOF

11 (X)

NaI (100) 4.1 (M) HATOF

4.9 (X)

KCl (100) 7.2 (M) HATOF

RbCl (100) 4.7 (M) HATOF

∼

5.7 (

Part 5 2.4

1018 Part 5 Special Structures

0000

––

–

ξξ ξ 1–ξ ξ0

–

NaCl (001)

ω (10

rad/s)

, S

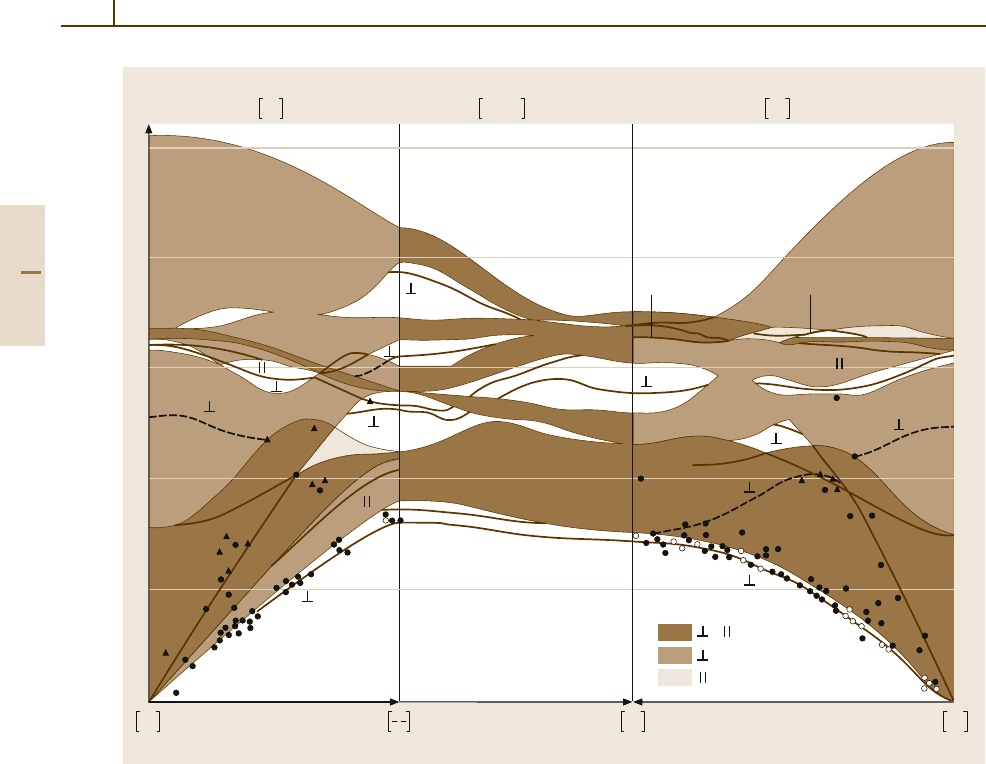
Fig. 5.2-57 Surface phonon dispersion curves for NaCl(100). Theoretical projected band structure (hatched) and exper-

imental points (dots) measured by HATOF. Solid and dashed lines represent theoretical surface states and resonances.

Ordinates are given in units of 10

rad/s = 6.586 meV [2.88,89]

Part 5 2.4

The Physics of Solid Surfaces 2.4 Surface Phonons 1019

1.0 1.0

–

––

–

[01] [11]

[0 0]

[ξ 0] [ξξ]

hω (meV)

–

––

–

Si (111) 2 ×1

–

Fig. 5.2-58 Surface phonon dispersion curves for Si(111)

2× 1 measured by HATOF. Energies at symmetry points:

X, 10.2 and 11.1meV; S, 10.5 and 11.6meV. The ﬂat

phonon mode at 10.5 meV is associated with the 2×1 recon-

struction. The surface mode couples with transverse bulk

phonons near the center of the SBZ, giving rise to consider-

able broadening. The shaded area corresponds to the width

of the 10.5 meV peak [2.90]. The energy of the optical mode

(not shown in the ﬁgure) is 56.0 meV [2.91]

5.2.4.3 Atom–Surface Potential

Many results on surface phonon dispersions are obtained

through atomic (mainly He) scattering.

The interaction of an incident atom with a surface

is described by the atom–surface potential (Fig. 5.2-59),

which consists of a hard repulsive part at short distances

and a weak van der Waals attraction at larger distances.

V (meV)

15.0

12.5

10.0

7.5

5.0

2.5

–2.5

–5.0

–7.5

–10.0

z (Å)

123456

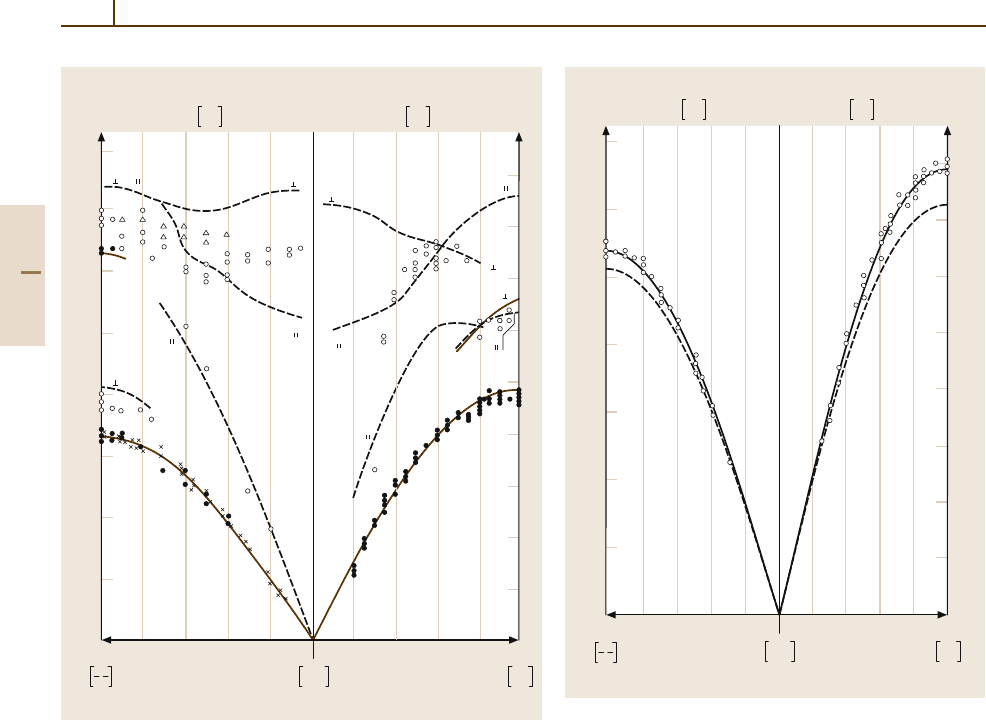
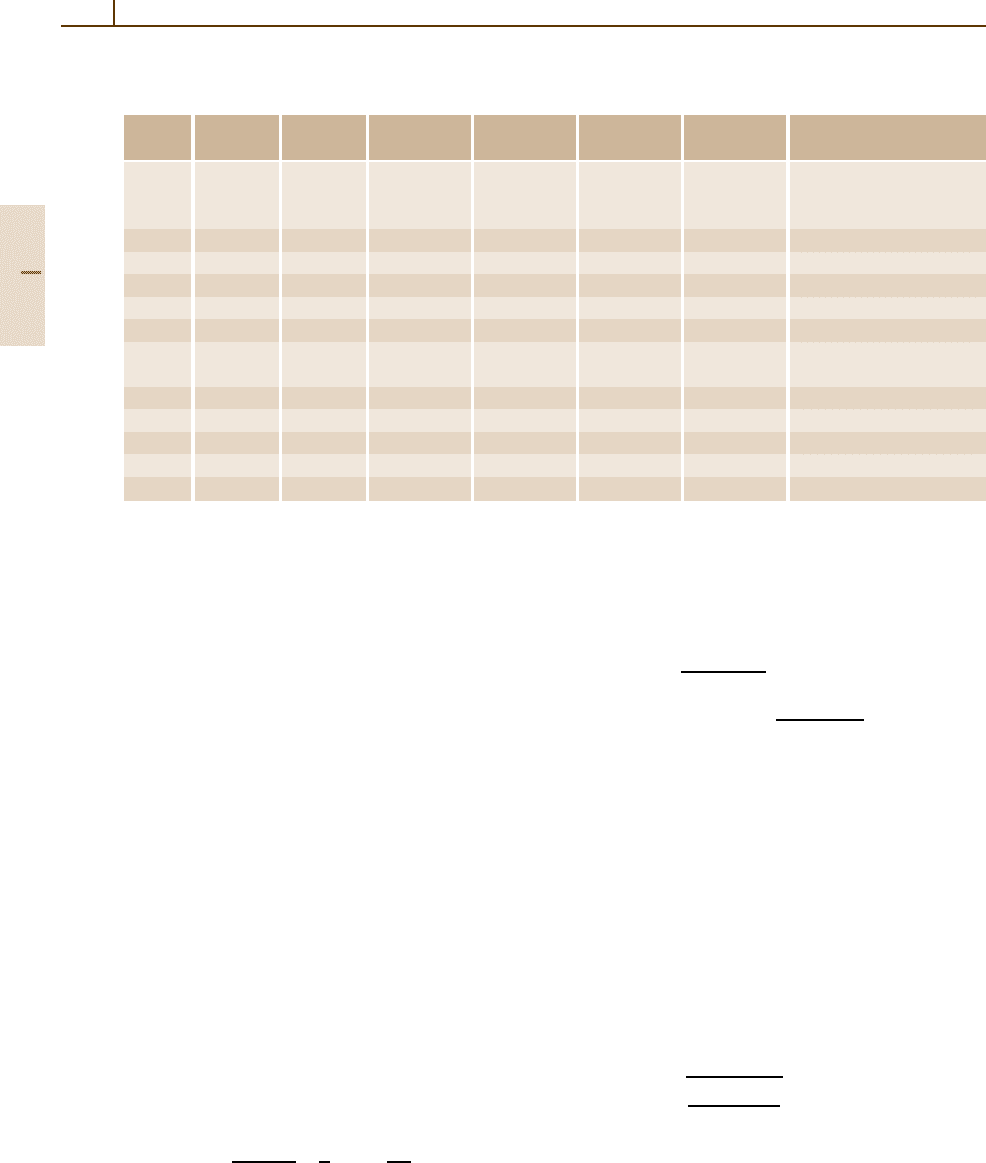
Fig. 5.2-59 Typical atom–surface potential, with deﬁni-

tions of the main interaction parameters. The surface unit

cell is shown in the inset. The numbers on the axes re-

fer to He–Ag(110) [2.92]. V

: surface averaged potential;

: potential at the top position; V

: potential at the bottom

position

The attractive contribution is often assumed in to be the

form

att

=−

(z −z

)

In the potential well between the van der Waals potential

and the hard repulsive potential, quantized energy lev-

els ε

exist (see Fig. 5.2-59). Table 5.2-24 summarizes

the parameters of the atom–surface potentials for a num-

ber of surfaces and impinging atoms (or molecules).

A more extended discussion is given in [2.14,15].

Part 5 2.4

1020 Part 5 Special Structures

Table 5.2-24 Parameters of the atom–surface potential. Values of ε

are given in the order n = 0, 1, 2, 3 .... References

to the original papers are given in [2.15]

Crystal Face Atom/ D (meV) z

(Å) z

(Å) C

(meV Å

) ε

(meV)

molecule

(110) H

31.7 3.27 0.755 714 25.3, 16.4, 9.7, 5.3, 2.5, 1.1

He 6.0 0.755 249 4.44, 2.18, 0.92, 0.31, 0.1

(111) H

32.5 2.5 0.2 714 25.5, 16.6, 9.9, 5.4, 2.5, 1.1

Al (110) He 5.2 4.47 1.71 202 3.65

Au (111) He 8.0 3.98 1.34 274 5.91

Cu (110) He 6.27 3.65 1.21 235 4.52, 2.2, 1.0, 0.3

GaAs (110) He (7) (3.5) (−0.2) (473) (4.2)

NaCl (100) He 6.1 3.49 1.03 106 4.1, 1.5, 0.31

LiF

(100) He 8.5 2.98 0.79 93 (137) 5.9, 2.46, 0.78, 0.21

Ne 13.5 192 11.7

Ni (100) He 4.2 (theory) 3.76 (theory) 218

Pd (110) He 8.05 3.60 211 6.42

Pt (110) 2×1 He 8.8 251 7.4, 5.1, 3.1, 1.5

Si (100) He 174

W (110) He 265 5.6

5.2.5 The Space Charge Layer at the Surface of a Semiconductor

Surface states in the gap of a semiconductor may trap

or loose electrons. The localized charge in surface states

is neutralized by a macroscopic space charge layer of

opposite sign, caused by accumulation or depletion of

the bulk carriers. The potential associated with the space

charge gives rise to a band bending of the bulk bands

at the surface. Band bending alters various properties

of semiconductor surfaces and is crucial for many ap-

plications, such as chemisorption, catalysis, corrosion,

and, most signiﬁcantly, channel conductivity in MOS

ﬁeld-effect transistors. For this reason, the problem of

the surface space charge layer is treated extensively in

the following sections.

5.2.5.1 Deﬁnitions and Notation

Figure 5.2-60 shows the main parameters that character-

ize the space charge layer. With reference to the ﬁgure,

the following deﬁnitions can be given:

•

(z) is the intrinsic level: this level runs parallel to

the band edges and coincides, in the bulk, with the

intrinsic Fermi level E

T ln

•

The following quantities related to band bending:

u(z) ≡

−E

(z)

v(z) = u(z) −u

≡

−E

(z)

(2.1)

where v

, u

,andu

are the values of v(z),andu(z)

at the surface and the value of u(z) in the bulk; u

> 0

for n-type semiconductors and u

< 0 for p-type

semiconductors. If v

> 0 the band bends downward;

if v

< 0 the band bends upward. v

= 0 is the con-

dition for ﬂat bands, and u

= 0 the condition for an

intrinsic surface.

An accumulation layer exists if v

and u

have the same

sign (as in Fig. 5.2-60).

An depletion layer exists if v

and u

have opposite signs

and u

have the same sign.

An inversion layer exists if both of the pairs v

, u

and

, u

have opposite signs.

•

Debye length:



+ p

)

(2.2)

where n

and p

are the bulk carrier concentra-

tions and q is the elementary charge. For small

Part 5 2.5

The Physics of Solid Surfaces 2.5 The Space Charge Layer at the Surface of a Semiconductor 1021

Table 5.2-25 Intrinsic Debye lengths for various semiconductors

Si Ge GaAs InP InAs InSb

Intrinsic Debye length (cm) 2.9×10

−3

7.0×10

−5

2.0×10

−1

2.7×10

−2

8.6×10

−6

2.4×10

−6

vac

u(z)k

ν(z)k

νs

Fig. 5.2-60 Schematic behavior of the bands at the surface

of a semiconductor and deﬁnition of the main parameters.

Notice that band bending v(z) is positive when the band

bends downward

bending (< k

T ), the surface barrier decays as

v(z) = v

−z/L

. Forlargerbending, the shape of the

potential cannot be givenin analytic form, though the

thickness of thespace charge layeris still on the order

of the Debye length (see Fig. 5.2-61). Values of the

intrinsic Debye length for various semiconductors

are given in Table 5.2-25. Figures 5.2-62 and 5.2-63

give L

as a function of the carrier density and bulk

resistivity for various semiconductors.

•

is the space charge density (per unit area), Q

is the charge density (per unit area) in surface states,

and

total

= Q

; (2.3)

total

=0 in the absence of an external electric ﬁeld.

In the presence of an external ﬁeld, Q

total

is the

charge density on the ﬁeld electrode (the gate in

a MOSFET).

Normalized potential ⏐v⏐= (eV/ kT)

–4

–8

–12

–16

2.0

Normalized distance z/L

0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8

Accumulation

layer

Inversion and

depletion layers

⏐u

⏐ⱜ 10

⏐u

⏐=8

⏐u

⏐=6

⏐u

⏐=4

⏐u

⏐=2

⏐u

⏐ⱜ 2

= 0

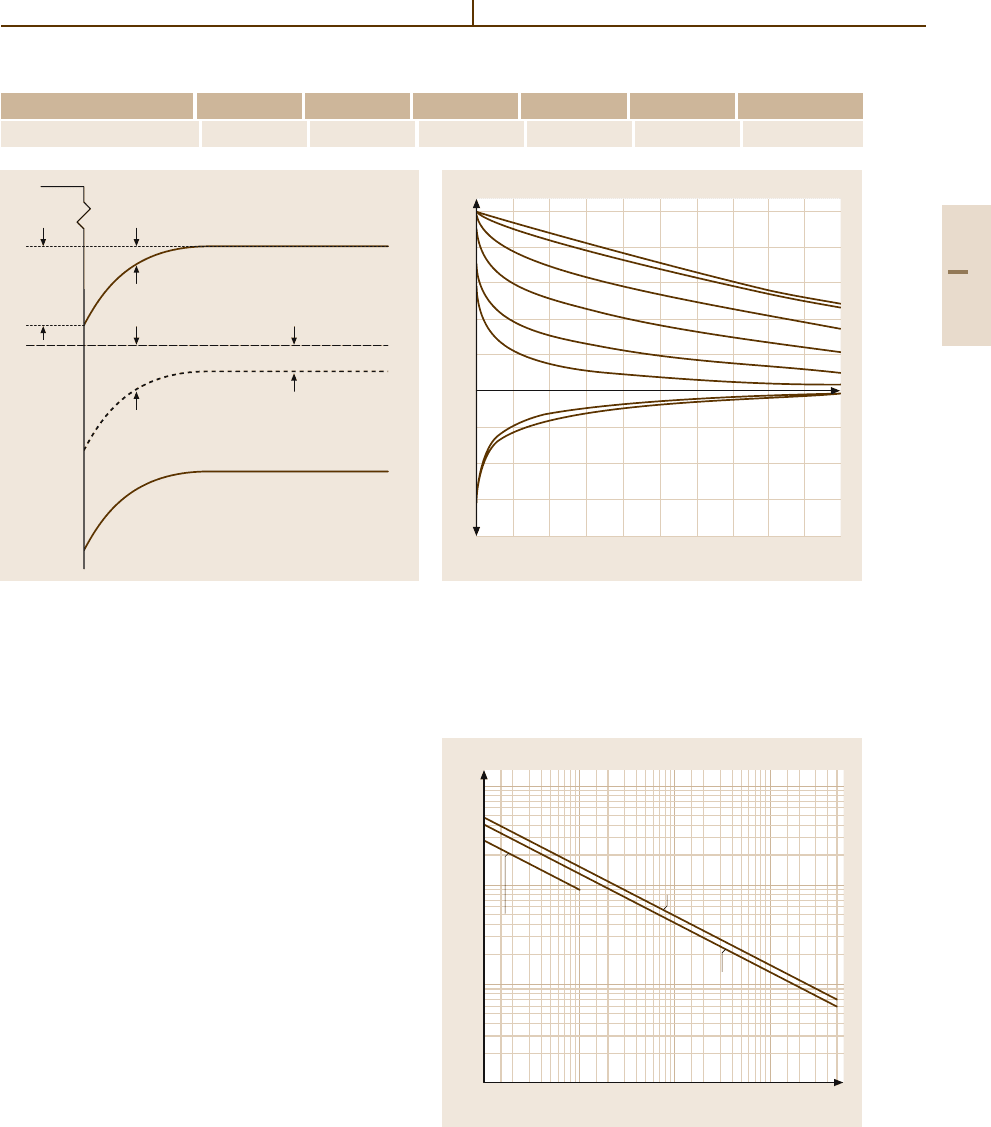
Fig. 5.2-61 Proﬁle of the potential |v(z)| as a function of

z/L

plotted for |v

|=20 and various values of |u

|.The

behavior for other values of |v

|can be obtained by drawing

the parallel to the abscissa through the new value |v



| and

translating the origin of the abscissa at the value of the

interception [2.48, p. 329]

(nm)

Carrier density (cm

–3

)

Ge(ε

= 16.2)

Si(

= 11.9)

p-type diamond

(

= 5.7)

Fig. 5.2-62 Debye length as a function of carrier concen-

tration for Si, Ge and p-type diamond

Part 5 2.5