Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.

2-16
REFERENCE
DATA
FOR ENGINEERS
Low
group
(hertz)
697
770
852
94 1
TABLE
6.
MULTIFREQUENCY NUMERICAL CODE
USED
BY
CCITT (TWO-OUT-OF-SIX)
Digit Frequencies Weighting
Low
group
(hertz)
1
2 3
1020
1
2
3
4 5 6 1140 4
5
6
7 8
9 1260 7 8 9
spare
0
spare
1380
0
1209 1336 1477 (1633)
High
1620 1740
1860
(1980)
High
group group
(hertz) (hertz)
1
700
+
900
0
+
1
2
700
+
1100
0
+
2
3 900
+
1100
1
+
2
4 700
+
1300
0
+
4
5
900
+
1300
1
+
4
6 1100
+
1300 2
+
4
7 700
+
1500
0
+
7
8 900
+
1500
1
+
7
9 1100
+
1500 2
+
7
0
1300
+
1500 4
+
7
Code
11
0
+
11
]
for inward
Code
12 900
+
1700
1
+
11
operators
KP 1100
+
1700 2
+
11
start of pulsing
KP2 1300
+
1700 4
+
11
transit traffic
ST
1500
+
1700 7
+
11
end of pulsing
700
+
1700
Continuous
signals
are based on conditions of on-
hook and off-hook, representing the condition of locked
or flowing direct current on the subscriber’s line, and
their extension
to
trunk signaling is given in Table
1
1.
Either condition is continuous and may be detected at
any time. On the other hand, discontinuous signals must
be recorded, and the condition represented is presumed
to continue until a new signal is sent. Supervisory
signaling in a backward direction (toward the calling
end) is
also
needed in automatic working and is also
described as on-hook or off-hook, although on two-wire
metallic circuits the signaling condition is usually a
reversal of flow of the direct current rather than an
interruption.
Continuous supervisory signaling over longer dis-
tances
is
effected by use of signaling paths distinct from
the voice path. These signaling paths may be telegraph
legs of a composite telegraph system, simplexing of the
voice pair, or special tones inside or outside of the voice
TABLE
7.
NUMERICAL FOUR-BY-FOUR MULTIFREQUENCY CODE
OFFICE
A
OFFICE
B
TRUNK SIGNALING SIGNALING TRUNK
CIRCUIT
SIGNALING
-48V
--c
-4xv
CONDITION AT CONDITION AT
SIGNAL SIGNAL SIGNALING CIRCUIT A SIGNALING CIRCUIT
B
AT0 B
BTOA
M
LEAD
ELEAD
MLEAD ELEAD
ON HOOK
ON-HOOK
GROUND
OPEN
GROUND OPEN
OFF HOOK
ON-HOOK
BATTERY
OPEN
GROUND GROUND
ON-HOOK
OFF-HOOK
GROUND
GROUND BATTERY
OPEN
OFF
HOOK
OFF-HOOK
BATTERY
GROUND BATTERY
GROUND
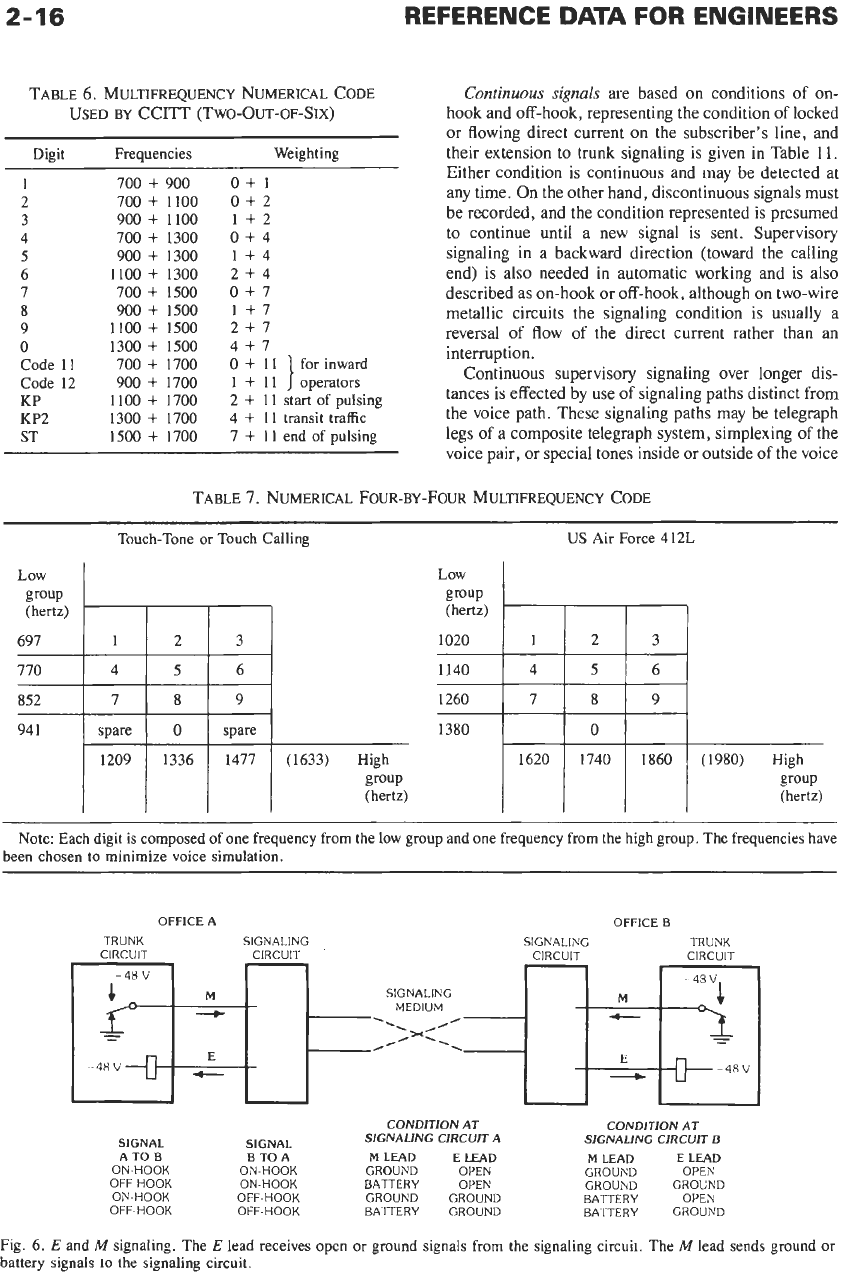
Fig.
6.
E
and
M
signaling. The
E
lead receives open
or
ground signals from the signaling circuit. The
M
lead sends ground
or
battery signals to the signaling circuit.

INTERNATIONAL TELEPHONY RECOMMENDATIONS
2-17
TABLE
8.
US
ARMY TA-341IPT
NUMERICAL CODE
Digit
1
2
3
4
5
6
7
8
9
0
Frequencies
2100
+
2300
2300
+
2500
1900
+
2700
1900
+
2100
2500
+
2700
2300
+
2700
2100
+
2500
1900
+
2300
2100
+
2700
1900
+
2500
channel. Whatever the paths, they are extensions of
separate direct-current leads from the trunk circuits,
known as
E
and
M
leads. The relation between the
conditions of these leads and the on-hook or off-hook
signaling conditions they represent is shown in Fig. 6.
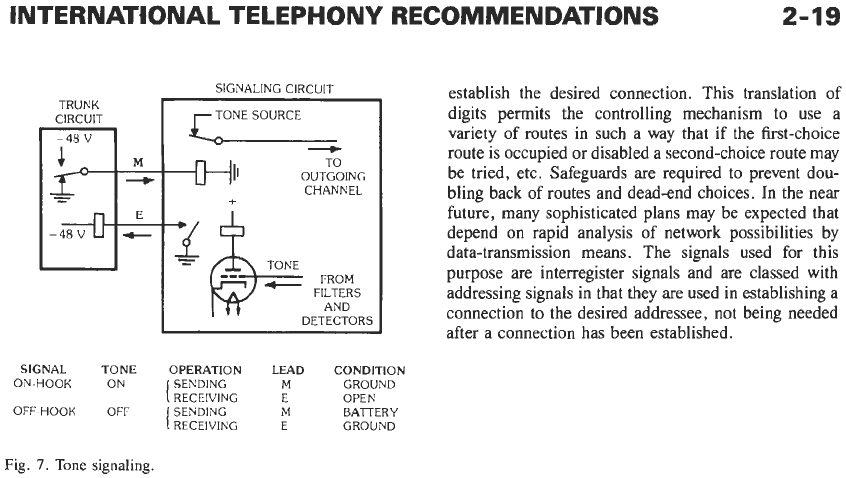
The usual method of extending the
E
and
M
leads over
tone channels is shown in Fig.
7.
The frequency of the
tone used is preferably higher than 2000 hertz and is
usually 2600 hertz on four-wire circuits. A 3825-hertz
signaling system is known as “out-of-band” and must
be built into the carrier system using it.
Spurt
signaling
avoids the necessity of using distinct
signaling paths. For manual operation, ringdown sig-
naling is usually satisfactory. For semiautomatic or
automatic operation, however, more elaborate systems
are required. Voice-frequency signals are used, and they
are distinguished from voice transmissions by filters and
timing. Single-frequency systems use one or two long
or short pulses of the specific signaling frequency, with
the pulses carefully timed to within minimum and
TABLE
9.
NUMERICAL CODE, TWO-VOICE-
FREQUENCY SIGNALING SYSTEM, CCITT NO.
4
Successive Elements
Digit
1 2
3
4
1
2
3
4
5
6
7
8
9
0
Y
Y
Y
Y
Y
Y
Y
X
X
X
Y
Y
Y
X
X
X
X
Y
Y
Y
Y
X
X
Y
Y
X
X
Y
Y
X
X
Y
Y
Y
Y
Y
X
X
X
X
Note: The two frequencies are sent one at a time, with a
silent space between pulses. The duration of both frequency
and silent periods is
35t7
milliseconds. Frequencies:
x
=
2040+.6
hertz;
y
=
240026
hertz. Power level:
-9
decibels.
maximum limits. Two-frequency systems use a gate-
opening prefix pulse of the two frequencies together,
followed, without a silent period, by a long or short
pulse of either of the two frequencies. The submarine-
cable signaling system (CCITT No. 5) uses two fre-
quencies in the “compel” mode, wherein the signal
frequencies are sent until acknowledged, and the ac-
knowledging signal is sent until the original signal is
stopped.
No
gate-opening prefix is used.
Ringdown
Signals
Ringdown signals
are
spurts of ringing current (16 to
25 hertz) applied usually through the ringing key of an
operator and intended to operate a bell, ringer, or drop
at the called end. The current may be generated by a
manually operated magneto or by a ringing machine
with or without automatically inserted silent periods.
Ringing to telephone subscribers in automatic central
offices is stopped or “tripped” automatically by relay
action resulting from the subscriber’s off-hook condi-
tion. Ringing signals may be converted to 500 or 1000
hertz, usually interrupted at a 20-hertz rate, to pass
through voice channels
of
carrier equipment.
A
ringing
signal to a manual switchboard usually lights a switch-
board lamp, which can be darkened again only by local
action and not by stopping or repeating the ringing
signal. This characteristic makes ringdown operation
unsuitable for fully automatic operation. Ringdown
signaling over carrier circuits has the advantages of
simplicity and of not requiring the distinct signaling
channels
of
E
and
M
systems.
Tones
A
special case of signaling is that of information in
the form of tones to the subscriber of a telephone
TABLE
10.
NUMERICAL CODE, ONE-VOICE-
FREQUENCY SIGNALING SYSTEM, CCITT
No.
3.
Time Elements
Digit Start
1
2 3 4
Stop
1
1
1
2
1
1
3
1
11
4
1 1
5
1
1
1
6
1
11
7
1
111
8
1
1
9 1
1
1
0
1 1 1
Note:
“1”
signifies frequency present. Length of each time
element is
50
milliseconds?
1
percent. Frequency:
2280+6
hertz. Power
level:
-6
decibels.

2-18
REFERENCE DATA FOR ENGINEERS
TABLE 11. ON-HOOK
AND
OFF-HOOK SIGNALS
Direct Current Telephone Line Trunk
On-hook signifies loop is open
to
direct current supplied
Off-hook signifies loop is closed, allowing relay at other
end to operate. Signaling in reverse direction is ring-
If
idle, signals on-hook to other end. Seizure at calling
end signals off-hook to called end. While calling end
awaits answer, called end signals on-hook to calling end.
from other end.
Answer results in signaling off-hook from called end.
system. The basic tones
are
dial tone, busy tone, and
ring-back tone (representing the, ringing of the called
subscriber’s line). The dial tone is generated at the
subscriber’s local switching center, but the busy tone
generated locally in accordance with spurt supervisory
signals from the called end.
Alternative Routing
and ring-back tone, plus special tones such as no-such-
number and line-out-of-order,
are
generated at the
called subscriber’s switching center and should be
Switching systems in which the complete called
standardized for universal intelligibility.
A
proposal by
the American Telephone and Telegraph Company for
standard tones is described in Table 12. On some
international calls, the busy and ring-back tones are
number is recorded in the first center to which the
subscriber is connected permit a translation of digits
from those identifying the called subscriber to those
most conveniently used by the switching mechanism
to
TABLE 12. TABLE
OF
PROPOSED STANDARD
OF
AUDIBLE TOND
IN
NORTH AMERICA
(FROM CCITT DOCUMENT AP
111-84)
~
Frequencies§ Power per Frequency
(hertz) at Exchange Where
Tone is Applied
Use
350 440 480 620 (dBmO) Cadence
Dial tone
X
X
-13
Continuous
Busy tone
X
X
-
24 0.5 second on
0.5 second off
Reorder tone*
X X
-
Audible ringing tone
High tone?
X
-
24
0.2
second on
0.3
second off
0.3 second on
0.2 second
off
or
-16
2
seconds on
4 seconds
off
-16 Varies according to
use
Preemption tone$
X X
-
18 Single 200/500-ms pulse
Call-waiting tone
X
-13
Single 500-ms pulse
Notes:
*
A
possible alternative is the
use
of a call-failure tone, which would identify the office and type of condition that prevented the
t
High tone is used in many ways. For example:
successful completion of the call.
(A)
(B)
(C)
Spurts of tone to indicate specific orders
to
operators in the manual service (order tones).
To inform operators of lines that
are
temporarily out
of
service (permanent signal tone).
To alert customers that their services are in a permanent off-hook condition.
$
Preemption tones are
used
in certain private switched networks which may interconnect with the national networks.
5
Frequency limits are 20.5 percent of nominal.
ENTERNATtONAL TELEPHONY RECOMMENDATIONS
2-19
establish the desired connection. This translation of
digits permits the controlling mechanism to use a
variety
of
routes in such a way that
if
the first-choice
route is occupied or disabled a second-choice route may
be tried, etc. Safeguards are required to prevent dou-
bling back of routes and dead-end choices. In the near
future, many sophisticated plans may be expected that
depend
on
rapid analysis
of
network possibilities by
data-transmission means. The signals used for this
purpose are interregister signals and are classed with
addressing signals
in
that they
are
used
in
establishing a
connection to the desired addressee, not being needed
after a connection has been established.
SIGNAL TONE OPERATION LEAD CONDITION
SENDING
M
GROUND
RECEIVING E OPEN
M
BATTERY
GROUND
ON-HOOK
ON
OFF-HOOK OFF
Fig.
7.
Tone
signaling.

Units,
Constants, and
Conversion Factors
Revised
by
Eugene
A.
Mechtly
SIUnits 3-2
SI Base Units
SI Derived Units
SI Prefixes
Additional Information on the SI
Units outside the
SI
Rules and Style Conventions
Dimensionless Quantities (Quantities of Dimension
1)
Decibels and Nepers
Numerical Values
Greek Alphabet
3-3
Fundamental Physical Constants
3-7
Conversion Factors 3-13
3-1

3-2
SI
UNITS”
TABLE
1.
SI
BASE
UNITS
There are two classes
of
units in the International
System
of
Units
(SI):
base units and derived units. The
units
of these two classes
form
a coherent set
of
units.
This coherent set of units is designated by the name
“SI
Units.”
SI
Base Units
The
SI
is founded on seven base units, respectively,
for seven base quantities. The base quantities are
assumed to be mutually independent. These base units
and base quantities are given in Table
1.
SI
Derived Units
Other quantities, called derived quantities, are defined
in
terms of the seven base quantities through a system of
quantity equations. Derived units for these derived quan-
*
The information
on
the
SI
in this chapter is based
on
Met-
ric System
of
Measurement: The International System
of
Units
for
the United States,
published in
the
US.
Federal Register,
Vol. 63, No. 144,1998, pp. 40334-40340.
This
Federal
Regis-
ter Notice can be viewed and downloaded over the World Wide
Web from the website of
the
US
Government Printing Office.
Go to www.gpo.gov. Click on “Federal Register,” select
“1998,” select “Notices,” and enter
“SI”
as
the
search term.
Base Quantity
Length
Mass
Time
Electric current
Thermodynamic temperature
Amount of substance
Luminous intensity
SI
Base Unit
Name Symbol
~ ~
meter m
kilogram kg
second
S
ampere A
kelvin
K
mole mol
candela cd
tities are obtained from the system of equations and the
seven base units
in
a coherent manner. Here, the term
coherent
is
used to mean a system of units where all
derived units are obtained
from
the base
units
by the
rules of multiplication and division, with no numerical
factor other than one
(1)
ever occurring
in
the expres-
sions for the derived units
in
terms
of
the base units.
Table
2
lists, in alphabetical order,
SI
derived units
and reiterates the seven
SI
base units.
SI
Prefixes
Table
3
gives the twenty
SI
prefixes used to form
decimal multiples and submultiples
of
SI
units.
TABLE
2.
SI
BASE
AND
DERIVED
UNITS
Name Symbol Quantity
ampere (an
SI
base unit) A electric current
ampere per meter A/m magnetic field strength
ampere per square meter A/m2 current density
becquerel Bq
sK1
activity
(of
a radionuclide)
candela (an
SI
base unit) cd luminous intensity
candela per square meter cd/m2 luminance
coulomb C s.A electric charge, quantity of electricity
coulomb per cubic meter c/m3 electric charge density
coulomb per
lulogram
Ckg exposure (x and gamma rays)
coulomb per square meter Clm‘ electric flux density
cubic meter
m-’
volume
cubic meter per kilogram m3kg specific volume
degree Celsius” “C Celsius temperature
farad
F
CN
capacitance
farad per meter Flm permittivity
gray
gray per second Gyls absorbed dose rate
henry
H
Wb/A inductance
henry per meter H/m permeability
hertz
Hz
sd
frequency
joule
J
N.m energy, work, quantity of heat
joule per cubic meter J/m3 energy density
joule per kelvin
J/K
heat capacity, entropy
joule per kilogram Jkg specific energy
joule per kilogram kelvin
joule per mole J/mol molar energy
joule
per
mole kelvin
*
The
kelvin (symbol
K)
is the
SI
unit of thermodynamic temperature,
T.
The degree Celsius (symbol “C) is the commonly used
GY
absorbed dose, specific energy imparted, kerma, absorbed dose index
J/(kg.
K)
J/(mol.
K)
specific heat capacity, specific entropy
molar entropy, molar heat capacity
unit
of
Celsius temperature,
t.
Celsius temperature
is
defined by the equation
t
=
T-
To,
where
To=
273.15 kelvins.
3-3
TABLE
2
(CONT).
BASE
AND
DERIVED
UNITS
Name Symbol Quantity
~~~~ ~
kelvin (an
SI
base unit)
kilogram (an
SI
base unit)
kilogram per cubic meter
kilogram per kilogram
lumen
lux
meter (an
SI
base unit)
meter per second
meter per second squared
mole (an
SI
base unit)
mole per cubic meter
newton
newton meter
newton per meter
number per meter
ohm
pascal
pascal second
radian
radian per second
radian per second squared
reciprocal meter
second (an
SI
base unit)
siemans
sievert
square meter
steradian
tesla
volt
volt per meter
watt
watt per meter kelvin
watt per square meter
watt per square meter steradian
watt per steradian
weber
K
kgkg
=
lm
IX
lm/m2
m
mls
m/s2
mol
mol/m3
N
N.m
Nlm
m-’
L2
VIA
Pa N/m2
Pa.s
rad
radls
rad/?
m-I
S
AN
sv
m2
T
wb/m2
V WIA
Vlm
W
Jls
Wl(m.K)
W/m2
W.
m-2. sr-1
Wlsr
wb
v.s
S
sr
1
thermodynamic temperature
mass
density, mass density
mass fraction
luminous flux
illuminance
length
speed, velocity
acceleration
amount of substance
concentration
(of
amount of substance)
force
moment
of
force
surface tension
wave number
electric resistance
pressure, stress
dynamic viscosity
plane angle
angular velocity
angular acceleration
wave number
time
electric conductance
dose equivalent, equivalent dose
area
solid angle
magnetic flux density
electric potential, potential difference, electromotive force
electric field strength
power, radiant flux
thermal conductivity
heat flux density, irradiance, power density
radiance
radiant intensity
magnetic
flux
TABLE
3.
SI
PREFIXES
Factor
1
oZ4
1021
10’8
1015
10’2
io9
106
io3
lo2
10
10-1
lo-*
Name
Symbol
yotta
zetta
exa
peta
tera
gigs
mega
kilo
hecto
deka
deci
centi
Y
Z
E
P
T
G
M
k
h
da
d
C
Example: In the expression
I
=
150 mA,
I
is the
symbol for a physical quantity (current), A is the
symbol for the unit of current (ampere), and m is
the symbol for the prefix milli. Together, m and
A
form
the symbol for a submultiple unit of current, the milli-
ampere.
Note that the kilogram, for historical reasons, is the
only
SI
unit
with a prefix
(kilo)
as part of its name
(kilogram) and as part of its symbol
(kg).
In
the special
case of the kilogram, the prefix names are used with
the name “gram” and the prefix symbols are used with
the symbol “g” for gram. For example, “mg”
is
the
symbol for milligram. With this exception, any
SI
pre-
fix may be used with any SI unit.
10-~
milli m
10-~
nano
n
ON THE
SI
1
0-15
femto f
Additional information on the SI may be found
in
10-18
atto a
the
NIST
Special Publication 811,
Guide
for
the Use
of
the International System
of
Units
(So,
by Barry N.
Taylor.
SP
811
is
for sale by the Government Printing
10-6
micro
P
ADDITIONAL INFORMATION
10-12
pic0 P
Z
zepto
Y
10-24
yocto

Office and is also available at the NIST website:
2.
www.physics.nist.gov/cuu.
Units outside the
SI
Certain units are not
part
of the International System
tant and widely used. The units
in
this category that are
approved for use in the United States, with the
SI,
are
of Units, that is, they are outside the SI but are impor-
given in Tables
4
and
5.
Rules and Style Conventions*
3.
4.
5.
6.
Rules and style conventions ensure that communi-
cation is not hindered by ambiguity. Some well-
established rules are:
7.
1.
Symbols for units and prefixes
are
printed in
Roman (upright) type regardless of the type used
in the surrounding text.
*
Most
of these rules and style conventions are copied
from the Federal Register Notice of 1998.
Uppercase and lowercase symbols
must
be used
for units and prefixes as defined in Tables
1
through
5
of this chapter. Failure to distinguish
between upper and lower cases of the same letter
is not acceptable. For example, mW (milliwatt)
and
MW
(megawatt)
must
not be confused.
When the name
of
a unit is spelled
out,
it
is
always written with a lowercase initial letter
unless it begins a sentence.
Unit symbols are unaltered
in
the plural,
Unit symbols are not followed by a period unless
at the end
of
a sentence.
Symbols for units formed from other units by
multiplication
are
indicated by means of a half-
high (that is, centered) dot or space. Example:
N.m
or
N
m.
Symbols for units formed from other units by
division are indicated by the means of a solidus
(oblique stroke,
0,
a horizontal line, or negative
exponents. For example,
m/s,
m
-,
or
m
.
s-’
S
TABLE
4.
UNITS
OUTSIDE
THE
SI
THAT
ARE
ACCEPTED
FOR
USE
WITH
THE
SI
Name Svmbol Value in
SI
Units
minute
hour
day
degree
minute
second
liter*
metric ton?
neper$
bel
time
1
plane angle
}
min
h
d
L
t
B
NP
1
min
=
60
s
1
h
=
60min
=
3600
s
1
d= 24 h= 86 400
s
I”=
(r/180)
rad
1’=(1/60)”=(r/10800)rad
1”= (1/60)’
=
(.ir/648
000)
rad
1
L
=
1
dm3
=
10”
m3
1
t
=
lo3
kg
1
Np=
1
1
B
=
11/2)
In
10
Nu
*
The liter and its symbol, 1, are approved for use internationally. The alternative symbol for the liter,
L,
was approved intema-
tionally in 1979
to
avoid the risk of confusion between the letter
1
and the number
1.
The prefened symbol for use in the United
States is
L.
Neither a lowercase script letter
1
nor an uppercase script letter
L
are approved symbols for the liter.
“metric
ton”
is also used
in
some other English-speaking countries. The name “tonne” is used in many other countries,
not
an
SI
unit.
t
The name “metric ton” is preferred for use in the United States for the unit with symbol t and
is
defined as
1
t
=
lo3
kg. The
j
Although the neper is coherent with
SI
units and is accepted by the
CIPM,
it has not been adopted by the
CGPM
and
is
thus
TA~LE
5.
UNITS
OUTSIDE
THE
SI
THAT
ARE
ACCEPTED
FOR
USE
WITH
THE
SI,
BUT WHOSE VALUES
IN
SI
UNITS
OBTAINED EXPERIMENTALLY
~
Name Symbol Value in
SI
Units*
~
electron voltt eV
1
eV
=
1.602 177 33(49)
x
J
astronomical units
unified atomic mass unit$
U
1
u
=
1.660
540 2(10)
X
kg
ua
1
ua
=
1.495 978 70(30)
x
10”m
*
The combined standard uncertainty (that is, estimated standard derivation) of the last two figures is shown in parentheses.
t
The electronvolt is the kinetic energy acquired by an electron in passing through
a
potential difference of
1
V
in vacuum.
$
The unified atomic mass unit is equal to 1/12 of the mass of an unbound atom of the nuclide
‘’C
at rest and
in
its ground state.
3
The astronomical unit is a unit of length approximately equal to the mean Earth-Sun distance.
Its
value
is
such that, when
used to describe the motion of bodies in the Solar System, the heliocentric gravitation constant is (0.017 202 098 95)’ ua3. d-’.

UNITS, CONSTANTS, AND CONVERSION FACTORS
3-5
However, to avoid ambiguity, the solidus must not
be repeated on the same line unless parentheses
are
used. Examples are
m/s2 or m.f2
but not:
m/s/s
m.kg/(s3.A) or m.kg.~-~.A-’
but not:
m.kg/s3/A
Negative exponents should be used in compli-
cated cases.
Prefixes symbols are printed in Roman (upright)
type regardless of the type used in the surround-
ing text and are attached
to
unit
symbols without
a space between the prefix symbol and the unit
symbol. This last rule also applies to prefix names
attached
to
unit names. Examples include
1
ml (one milliliter)
1
pm (one picometer)
1
Gfl
(one gigaohm)
1
THz (one terahertz)
The grouping formed by a prefix symbol attached
to a unit symbol constitutes a new inseparable
symbol (forming a multiple or submultiple
of
the
unit concerned), which can be raised
to
a positive
or negative power and which can be combined
with other unit symbols to form compound unit
symbols. Some examples are
2.3 cm3
=
2.3 (~rn)~
=
2.3 (10-2m)3
=
2.3
x
10-6m3
I
cm-’
=
1
(cm)-’
=
1
(10-2m)-’
=
lo2
m-’
5000
ps-’
=
5000
(ps)-’
=
5000
(lo-%-’
=
5000
x
10%’
=
5
x
lo9
s-’
Prefix names are also inseparable from the
unit
names to which they
are
attached. Thus, for
example, millimeter, micropascal, and meganew-
ton
are
single words.
10.
Compound prefix symbols, that is, prefix symbols
formed by the juxtaposition of two or more prefix
symbols, are not permitted. This rule also applies
to compound prefix names. For example,
1
nm (one nanometer)
but not:
1
mpm (one
millimicrometer)
11.
An
SI
prefix symbol (and name) cannot stand
alone but must be attached to a unit symbol (or
name). For example,
5
x
106/m3
but not:
5
M/m3
12.
In
the
expression for the value of
a
quantity,
the
unit symbol is placed after the numerical value
and a space is left between the numerical value
and the unit symbol. The only exceptions to the
rule are for the unit symbols for degree, minute,
and second for plane angle:
”,
‘,
and
”,
respec-
tively (see Table
4),
in which case no space is left
between the numerical value and the unit symbol.
For example,
a
=
30”22‘8”
This rule means that:
(a) The symbol “C for the degree Celsius is pre-
ceded by a space when one expresses the val-
ues of Celsius temperatures. Thus
t
=
30.2 “C
but not: t
=
30.2”C or
t
=
30.2” C
(b) Even when the value of a quantity is used in
an adjectival sense, a space is left between the
numerical value and the unit symbol. (This
rule recognizes that unit symbols are not like
ordinary words or abbreviations but are math-
ematical entities and that the value of a quan-
tity should be expressed in a way that is as
independent of language as possible.) Some
examples are
a 1
m
end gauge
but not:
a 1-m end gauge
a
10
kfl resistance
but not:
a 10-kfl resistance
However, if there is any ambiguity, the words
should be rearranged accordingly. For example,
the statement “the samples were placed in 22 mL
vials” should be replaced with the statement “the
samples were placed in vials of volume 22
mL”
or “the samples were placed in 22 vials of volume
1
mL,” whichever was meant.
NOTE: When unit names are spelled out as is
often the case in nontechnical writing, the normal
rules of English apply.
Thus,
for example, “a roll
of 35-millimeter film” is acceptable.
When there is a risk of confusion in using the
standard symbol (e.g.,
“s”
or
“T”)
the name of the
unit should be spelled out (e.g., second or tesla).
When a rarely used multiple or submultiple of
an
SI
unit is first used in text, the full name should
be stated. Subsequently, the corresponding sym-
bols may be used alone. For example:
The
solar
energy incident each year at the top of the Earth’s
atmosphere is about
5.6
yottajoules
(5.6
YJ).
The
total energy of a solar
flare
is about
10Y.J.
Dimensionless Quantities
(Quantities
of
Dimension
I)
Ratios of two quantities of the same dimension are
called
dimensionless quantities
or
quantities
of
dimen-
sion
1.
They are expressed as pure numbers. The
SI
unit
of
all dimensionless quantities is the number
1.
The two quantities may be of the same kind or they
may be of a different kind.
Examples of dimensionless ratios of quantities of
the same kind are: relative permittivity, relative per-
meability, refractive index, mass fraction, and charac-
teristic numbers (e.g., Mach number and Reynolds
number).
Examples of dimensionless ratios
of
quantities of
different kinds are the radian, with unit symbol rad for
plane angle (arc length divided by radius), and the
steradian, with unit symbol sr, for solid angle (area
divided by radius squared). The special names, radian
