Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.

130
Глава
4.
Построение
моделей
систем
управления
же
случаях,
когда
не
все
переменные
состояния
доступны
измерению,
для
реали
зации
регуляторов
состояния
требуется
привлечение
систем
оценивания
неизме
ряемых
переменных
(наблюдателей,
см.
1.5.3
и
п.
7.4),
в
сочетании
с
которыми
рассматриваемые
регуляторы
приобретают
динамический
характер
(см.
п.
7.5).
Теперь
рассмотрим
систему
с
регулятором
комбинированного
типа,
который
поз
воляет
обеспечить
наиболее
эффективную
компенсацию
отклонений,
вызванных
возмущением
f(t)
и
текущими
вариациями
задания
y*(t).
Такой
регулятор
в
пред
rюложении,
что
размерности
векторов
х
и
х*
совпадают,
описывается
уравнением
[алгоритмом
управления)
вида
и
=
Ke+Lx*+Lf~,
(4.94)
'де
L
и
L f -
матрицы
прямых
связей
по
задающему
и
возмущающему
воздей
~твиям
соответственно
(см.
рис.
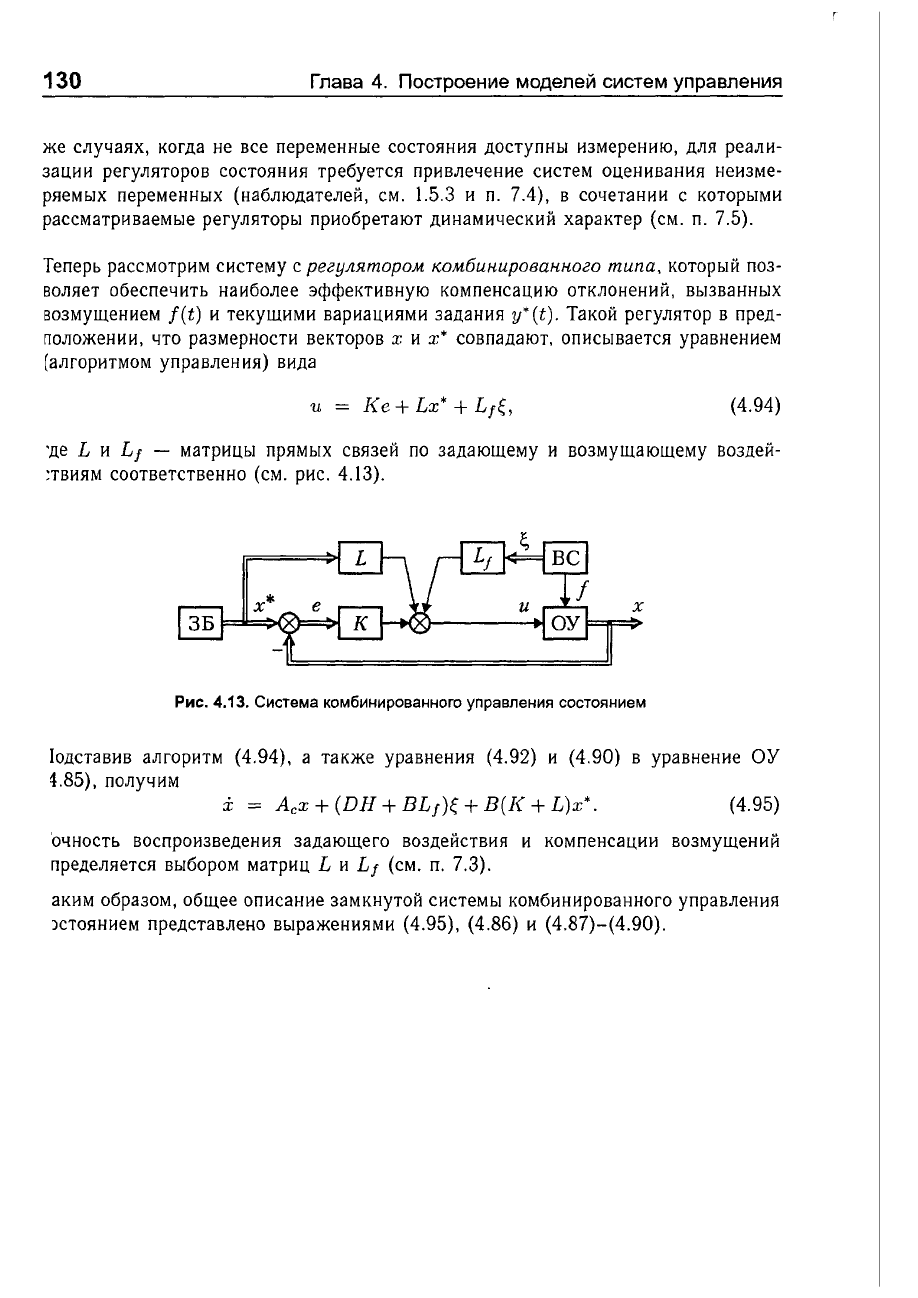
4.13).
Рис.
4.13.
Система
комбинированного
управления
состоянием
lодставив
алгоритм
(4.94),
а
также
уравнения
(4.92)
и
(4.90)
в
уравнение
ОУ
1.85),
получим
(4.95)
'очность
воспроизведения
задающего
воздействия
и
компенсации
возмущений
пределяется
выбором
матриц
L
и
Lf
(см.
п.
7.3).
аким
образом,
общее
описание
замкнутой
системы
комбинированного
управления
)стоянием
представлено
выражениями
(4.95), (4.86)
и
(4.87)-(4.90).

Глава
5.
Устойчивость
~
и
структурные
своиства
в
этом
разделе
изучаются
основные
свойства
динамических
систем
-
свойства
устойчивости,
управляемости
и
наблюдаемости.
При
исследовании
устойчивости
(п.
5.1-5.2)
анализируется
система
автоматического
управления
в
целом,
т.
е.
«го
товая»
(обычно
замкнутая)
система,
содержащая
объект
управления,
а
также
ре
гулятор
и
другие
необходимые
функциональные
блоки,
построенные
одним
из
из
вестных
методов
синтеза
(см.
главу
7).
При
этом
свойство
устойчивости
выступает
в
качестве
безусловного
требования
к
качеству
процессов
управления.
Концепции
управляемости
и
наблюдаемости
(п.
5.3)
связаны
со
структурными
особенностями
самого
объекта
управления
и
позволяют
установить
принципиаль
ную
возможность
решения
основных
задач
проектирования
САУ
-
задач
синтеза
управления
и
оценивания
состояний
объекта
(наблюдения).
5.1.
УСТОЙЧИВОСТЬ
систем
управления
Концепция
устойчивости
в
теории
автоматического
управления
являются
осно
вопологающеЙ.
Первые
работы,
посвященные
анализу
устойчивости,
относятся
к
второй
половине
XIX
века
и
связаны
с
именами
ДЖ.
К.
Максвелла,
И.
А.
Вышне
градского,
А.
Б.
Стодолы,
Е.
ДЖ.
Рауса
и
А.
Гурвица.
Наиболее
важные
резуль
таты
в
этой
области,
получившие
широкое
распространение
в
современной
теории
управления,
при
надлежат
А.
М.
Ляпунову
(1892
г.).
Под
устойчивостью
понимают
способность
динамической
системы
возвращаться
в
равновесное
состояние
(положение
равновесия)
по
сле
окончания
действия
внешних
факторов.
При
исследовании
устойчивости
линейных
стационарных
систем
следует
учиты
вать
следующее:

132
Глава
5.
Устойчивость
и
структурные
свойства
о
Н.у.!
х
у
~Системаt=1
===>----..
а)
рассматривается
движение
автономной
систе
мы,
описываемой
уравнением
а(р)
y(t) =
О,
или
поведение
модели
состояние-выход
±(t) =
Ax(t),
y(t)
Cx(t),
(5.1)
(5.2)
(5.3)
что
соответствует
свободному
движению
возмущенной
системы
и
переменым
YCB(t)
и
XCB(t);
б)
поведение
системы
анализируется
при
ненулевых
начальных
условиях:
у(О)
i=
О
или
х(О)
i=
О соответственно;
в)
под
равновесным
состоянием
(см.
2.2.2
и
3.1.2)
понимают
установившееся
со
стояние
автономной
системы
у
=
у*
или
х
=
х*.
Равновесное
состояние
находится
из
условия
± =
о
или
уи)
=
О,
i =
О,
n.
Для
линейной
модели
(5.1)
при а
n
i=
о
получаем
значение
у*
=
О,
а
для
модели
(5.2)
при
det
А
i=
О
находим:
х*
=
О.
Различают
следующие
концепции
устойчивости:
•
устойчивость
ПО
выходу,
или
техническую
устойчивость;
•
устойчивость
по
состоянию,
или
математическую
устойчивость.
Как
показано
ниже,
при
определенных
условиях
указанные
понятия
оказываются
эквивалентными.
5.1.1.
Техническая
устойчивость
в
технических
приложениях
нашли
распространение
упрощенные
определения
устойчивости
[4,
39]
и
понятия
устойчивой,
нейтрально
устойчивой
и
неустой
чивой
системы
(или
устойчивого,
нейтрально
устойчивого
и
неустойчивого
движе
ния),
определяемые
характером
изменения
выходной
переменной
y(t) -
решения
системы
(5.1)
y(t) = y(t,
Уа, Уа,
..
. ,
y~n-l»)
или
соответствующего
выхода
системы
(5.2), (5.3).
(5.4)
Определение
5.1.
Система
(или
движение
системы
относительно
положения
рав
новесия
у*
=
О)
называется
устойчивой,
если
с
течением
времени
(при
t
-+
00)
она
возвращается
в
положение
равновесия
(рис.
5.1),
т.
е.
lim y(t) =
О.
t-oo
(5.5)

5.1.
УСТОЙЧИВОСТЬ
систем
управления
У
УО
о
(а)
t
Рис.
5.1.
Апериодический
(а)
и
колебательный
(б)
процессы
устойчивой
системы
133
Определение
5.2.
Система
(или
движение
системы
относительно
положения
рав
новесия
у*
=
О)
называется
н,ейтралыю
устойчивой,
если
для
любых
t >
О
она
остается
в
некоторой
окрестности
положения
равновесия
(рис.
5.2),
т.
е.
найдется
число
6 >
О
такое,
что
для
любых
t
~
О
выполняется
У
УО
о
(а)
ly(t)1
<
6.
(5.6)
t
Рис.
5.2.
Апериодический
(а)
и
колебательный
(б)
процессы
нейтрально
устойчивой
системы
Определение
5.3.
Система
(или
движение
системы
относительно
положения
рав
новесия
у*
=
О)
называется
н,еустойчивой,
если
с
течением
времени
она
покидает
любую
наперед
заданную
6-0крестность
положения
равновесия
(рис.
5.3),
т.
е.
для
любых
6 >
О
найдется
t*
>
О
такое,
что
при
t >
t*
имеет
место
ly(t)1
>
6.
(5.7)
Для
большинства
апериодических
процессов
неустойчивое
движение
характеризу
ется
неограниченным
возрастанием
модуля
выходной
переменной
Нт
ly(t)1
=
00,
t-+co
(5.8)
а
для
колебательных
-
увеличением
амплитуды.
Замечан,ие
5.1.
Использование
приведенных
определений
не
приводит
к
противо
речиям
при
рассмотрении
линейных
полностью
наблюдаемых
(см.
п
5.3.2)
систем.
Для
н,елин,ейн,ых
систем
[3,
26,
27,
30]
возможны
случаи,
когда:

134
Глава
5.
Устойчивость
и
структурные
свойства
t
Рис.
5.3.
Апериодический
(а)
и
колебательный
(б)
процессы
неустойчивой
системы
•
выходная
переменная
сначала
неограниченно
возрастает
(неравенство
(5.7)),
а
затем
приближается
к
положению
равновесия
(выражение
(5.5));
•
система
имеет
несколько
положений
равновесия,
обладающих,
вообще
гово
ря,
разными
свойствами;
•
свойства
системы
существенно
зависят
от
начальных
отклонений
от
положе
ния
равновесия.
Для
не
полностью
наблюдаемых
систем
поведение
выходной
переменной
не
дает
однозначного
представления
о
характере
изменения
других
переменных
состояния,
например,
при
затухании
процесса
y(t)
частично
устойчивой
системы
(см.
[26,27,
зо,
З8])
некоторые
промежуточные
переменные
могут
неограниченно
возрастать.
Примером
нейтрально
устойчивой
системы
слу
жит
обычный
маятник
в
вакууме.
Маятник
в
y(t)
вязкой
среде
относится
к
устойчивым
системам,
а
перевернутый
маятник
является
неустойчивой
системой.
К
нейтрально
устойчивым
системам
от
носятся
интегрирующие
и
консервативные
зве
нья;
апериодические
и
колебательные
звенья
-
устойчивы.
5.1.2.
ПОНЯТИЯ
математической
устойчивости
Более
совершенные
определения
устойчивости
были
введены
А.
М.
Ляпуновым
для
анализа
свойств
отдельных
решений
х*
(t,
ха)
динамических
систем
общего
вида
(см.
[З,
16,
зо,
44]).
Аналогичные
понятия
могут
быть
использованы
и
для
исследования
устойчивости
стационарных
решений
(положений
равновесия)
ли
нейных
систем,
т.
е.
анализа поведения
в
пространстве
состояний
lR
n
автономной
системы
управления
(5.2)
относительно
начала
координат
-
точки
х*
=
О.
Рассмотрим
решения
уравнения
(5.2):
x(t) = x(t,
ха)
(5.9)

5.1.
УСТОЙЧИВОСТЬ
систем
управления
135
и
введем
евклидову
норму,
которая
характеризует
текущее
отклонение
системы
от
положения
равновесия
(равновесного
состояния)
х*
=
О:
Ix(t)1
=
Vx(t)Tx(t)
или
Ix(t)lp =
VxT(t)Px(t),
где
Р >
о
-
весовая
матрица.
Определение
5.4.
Система
(равновесное
состояние
х*
=
О)
называется
устойчивой
по
Ляпунову,
если
для
любого
е
>
О
найдется
б(е)
>
О
такое,
что
для
всех
начальных
значений
хо
из
области
'хоl
<
б
(5.10)
и
для
любых
t >
О
выполняется
Ix(t,xo)1 <
6.
(5.11)
Определение
предусматривает,
что
траектории
(5.9)
системы
(5.2),
начинающиеся
в
не
которой
(может
быть,
достаточно
малой)
б-окрестности
положения
равновесия,
не
покидают
заданную
е-окрестность.
Замечание
5.2.
Для
рассматриваемого
здесь
класса
линейных
стационарных
си
стем
условия
устойчивости
по
Ляпунову
эквивалентны
ограниченности
всех
реше
ний уравнения
(5.2)
(траекторий
системы)
для
любых
t
вне
зависимости
от
выбора
начальных
значений
хо.
Определение
5.5.
Система
(равновесное
состояние
х*
=
О)
называется
неусmойчивой,
если
существует
такое
значение
е
>
О,
что
для
любых
сколь
угодно
ма
лых
д
>
О
найдется
начальное
состояние
ха
из
области
(5.10),
для
которого
условие
(5.11)
нарушается.
В
отличие
от
понятия
устойчивой
системы
(определе
ние
5.4)
в
определении
5.5
предполагается,
что
неко
торые
траектории
(5.9)
системы
(5.2),
начинающиеся
в
сколь
угодно
малой
д-окрестности
положения
равнове-
сия
могут
выйти
за
пределы
некоторой
е-окрестности.
Замечание
5.3.
Для
рассматриваемого
здесь
класса
линейных
стационарных
си
стем
условия
неустойчивости
соответствуют
возможности
получения
неограничен
ных
решений
уравнения
(5.2)
(неограниченных
траекторий).
Определение
5.6.
Система
(равновесное
состояние
х*
=
О)
называется
асимnто
тически
устойчивой,
если
136
Глава
5.
Устойчивость
и
структурные
свойства
(а)
система
устойчива
по
Ляпунову;
(6)
выполняется
условие
аттрактивности
(притяжения)
положения
равновесия:
lim x(t,
ха)
=
О.
t-oo
(5.12)
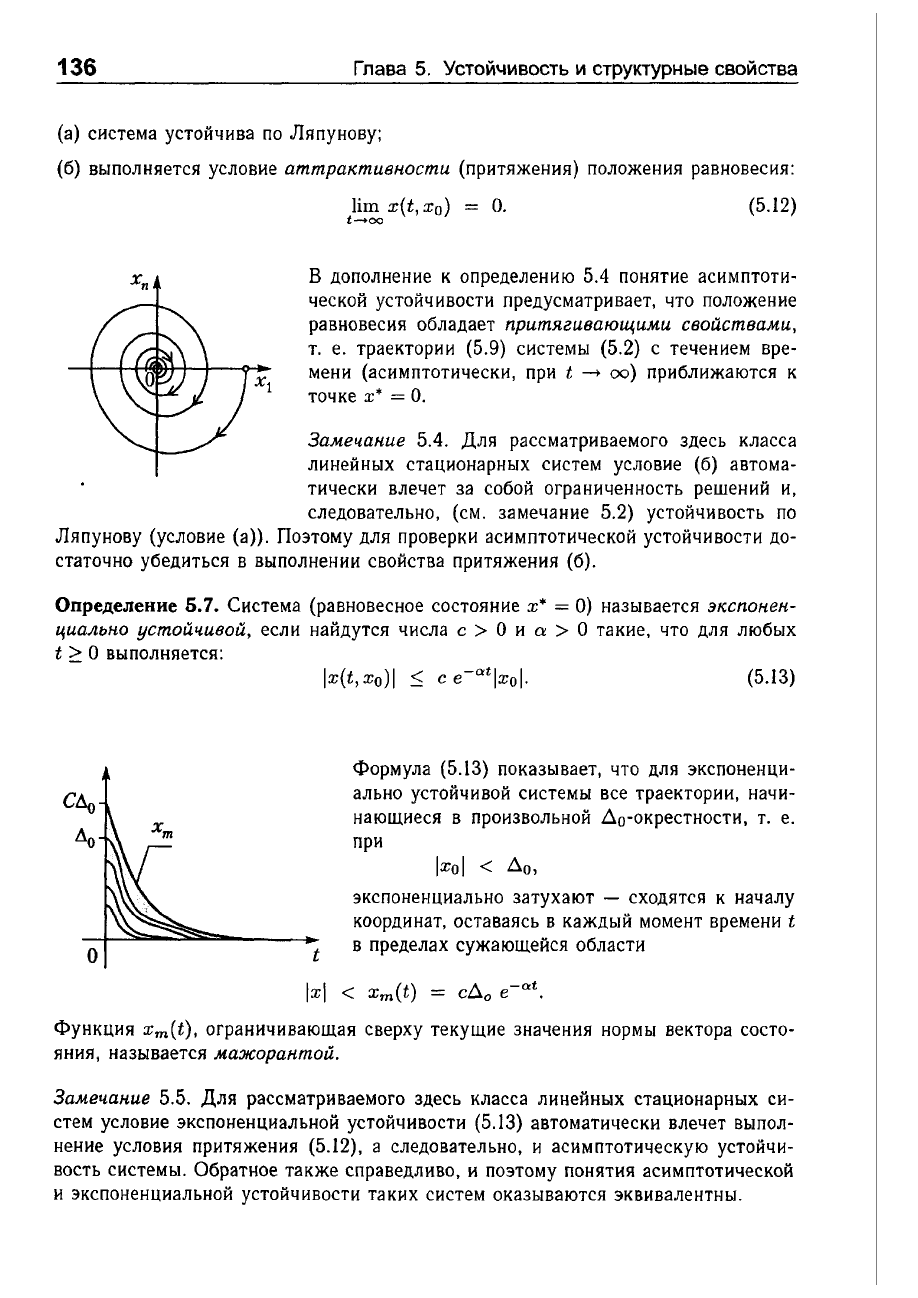
в
дополнение
к
определению
5.4
понятие
асимптоти
ческой
устойчивости
предусматривает,
что
положение
равновесия
обладает
притягивающими
свойствами,
т.
е.
траектории
(5.9)
системы
(5.2)
с
течением
вре
мени
(асимптотически,
при
t
---+
00)
приближаются
к
точке
х*
=
О.
Замечание
5.4.
Для
рассматриваемого
здесь
класса
линейных
стационарных
систем
условие
(б)
автома
тически
влечет
за
собой
ограниченность
решений
и,
следовательно,
(см.
замечание
5.2)
устойчивость
по
Ляпунову
(условие
(а)).
Поэтому
для
проверки
асимптотической
устойчивости
до-
статочно
убедиться
в
выполнении
свойства
притяжения
(б).
Определение
5.7.
Система
(равновесное
состояние
х*
=
О)
называется
экспонен
циально
устойчивой,
если
найдутся
числа
с
>
О
и
а
>
О
такие,
что
для
любых
t
~
О
выполняется:
о
t
(5.13)
Формула
(5.l3)
показывает,
что
для
экспоненци
ально
устойчивой
системы
все
траектории,
начи
нающиеся
в
произвольной
до-окрестности,
т.
е.
при
'хоl
<
до,
экспоненциально
затухают
-
сходятся
к
началу
координат,
оставаясь
в
каждый
момент
времени
t
в
пределах
сужающейся
области
'хl
< xm(t) =
сд
о
e-
at
•
Функция
xm(t),
ограничивающая
сверху
текущие
значения
нормы
вектора
состо
яния,
называется
.м.ажорантоЙ.
Замечание
5.5.
Для
рассматриваемого
здесь
класса
линейных
стационарных
си
стем
условие
экспоненциальной
устойчивости
(5.13)
автоматически
влечет
выпол
нение
условия
притяжения
(5.12),
а
следовательно,
и
асимптотическую
устойчи
вость
системы.
Обратное
также
справедливо,
и
поэтому
понятия
асимптотической
и
экспоненциальной
устойчивости
таких
систем
оказываются
эквивалентны.

5.1.
УСТОЙЧИВОСТЬ
систем
управления
137
Для
линейных
стационарных
полностью
наблюдаемых
систем
(см.
5.3.2)
легко
получить
связь
основных
понятий
технической
и
математической
устойчивости:
Техническая
устойчивость
~атематическая
устойчивость
Система
нейтрально
устойчива
Система
устойчива
по
Ляпунову
Система
устойчива
Система
асимптотически
устойчива
Система
неустойчива
Система
неустойчива
5.1.3.
УСТОЙЧИВОСТЬ
возмущенных
систем
Нормальное
функционирование
системы
предусматривает
действие
на
нее
внешних
факторов,
проявляющееся
в
виде
возмущающих
и
задающих
воздействий.
Поэто
му
стандартные
подходы
к
исследованию
устойчивости,
относящиеся
к
движению
автономных
моделей,
могут
показаться
непрактичными.
Тем
не
менее
результаты
анализа
устойчивости
позволяют
также
судить
о
свойствах
возмущенной
системы.
у* у
4Система~
Прuм.ер
5.1.
Рассмотрим
поведение
системы
а(р)у
=
Ьу*
с
характеристическим
полиномом
(
)
n
n-l
ар
=
р
+
alP
+ ... +
а
n
,
(5.14)
на
вход
которой
поступает
постоянное
задающее
воздействие
у*
= const,
и
а
n
=1=
О.
Целью
работы
системы
является
поддержание
выходной
пере
мен
ной
на
заданном
уровне
у*
(задача
стабилизации,
см.
1.4.1),
т.
е.
y(t) =
у*
= const.
(5.15)
Выясним,
какими
свойствами
должна
обладать
система
для
устойчивого
выполне
ния
условия
(5.15).
Рассмотрим
частное
решение
уравнения
(5.14)
ь
*
Уу
=
-у
а
n
и
функцию
(переходную
составляющую,
см.
замечание
2.2)
Ду
=
Уу
-
у.
Преобразуем
модель
системы
(5.1),
учитывая,
что
а(р)ду
=
а(р)уу
-
а(р)у
=
аnу
у
-
Ьу*.
(5.16)
(5.17)

138
Глава
5.
Устойчивость
и
структурные
свойства
Принимая
во
внимание
(5.16),
получим
уравнение
преобразованной
модели
а(р)ду
=
О.
(5.18)
Выражение
(5.18)
в
точности
повторяет
уравнение
автономной
системы
(5.1),
и
по
этому
свободные
составляющие
систем
(5.14)
и
(5.18)
идентичны,
что
определяет
эквивалентность
свойств
устойчивости.
Если
основная
модель
(5.14)
(асимптоти
чески)
устойчива,
то
устойчивой
является
и
преобразованная
модель
(5.18),
т.
е.
для
любых
начальных
условий
выполняется
lim
ду(t)
t-.oo
О.
(5.19)
Учитывая
(5.19)
и
(5.17),
запишем
lim y(t) =
Уу.
t
......
oo
(5.20)
Таким
образом,
для
устойчивой
системы
(5.14)
выходная
переменная
всегда
асимп
тотически
стремится
к
значению
Уу.
Если
при
этом
выполняется
а
n
=
Ь,
то
из
уравнения
(5.16)
получаем
*
Уу
=
у
,
(5.21)
и
следовательно,
выход
системы
с
течением
времени
совпадает
с
задающим
воз
действием,
что
и
является
целью
ее
работы
(уравнение
(5.15».
Для
нейтрально
устойчивой
системы
(5.14)
можно
гарантировать
ограниченность
переходной
составляющей
ду
и,
следовательно
(при
условии
а
n
=
Ь),
-
выпол
нение
условия
(5.15)
с
некоторой
ограниченной
ошибкой.
Неустойчивая
система
характеризуется
неограниченным
ростом
ду,
что
влечет
за
собой
расходимость
функций
y(t)
и у*
(t),
т.
е.
невыполнение
цели
управления.
О
Теперь
рассмотрим
общий
случай
движения
замкну
тых
возмущенных
систем,
описываемых
уравнениями
вход-выход
а(р)у
=
Ь(р)у*
+ d(p)J,
(5.22)
где
входными
сигналами
являются
задающие
воздействия
y*(t)
и
возмущения
J(t).
Соответствующие
выходные
переменные
могут
быть
представлены
в
форме
(см.
п.
2.2
и
3.2)
y(t) =
YCB(t)
+
YB(t),
(5.23)
где
вынужденная
сос'тавляющая
YB(t)
обусловлена
действием
указанных
выше
внешних
факторов,
а
составляющая
YCB(t)
определяет
свободное
движение
систе
мы,
непосредственно
связанное
со
свойством
устойчивости.
Цель
работы
системы,
предназначенной
для
решения
задачи
стабилизации
или
слежения
(см.
1.4.1),
заключается
в
обеспечении
желаемого
изменения
выходной

5.1.
УСТОЙЧИВОСТЬ
систем
управления
139
переменной
y(t),
т.
е.
выполнение
(с
заданной
степенью
точности)
целевого
усло-
вия
y(t) =
у*
(t).
(5.24)
Учитывая
однако,
что
в
начальный
момент
работы
системы
переменные
y(t)
и
y*(t)
обычно
не
совпадают,
более
реалистично
потребовать
асимптотического достиже
ния
условия
(5.24),
т.
е.
его
выполнения
в
установившемся
режиме
(см.
2.2.4):
yy(t) =
у*
(t).
(5.25)
где
yy(t) -
установившаяся
составляющая
переходнога
процесса
(рис.
5.4).
Будем
полагать,
что
система
спроектирована
так,
что
при
соответствующих
на
чальных
условиях
уи)
(О)
тождество
(5.24)
выполняется
с
абсолютной
точностью.
В
этом
случае
решение
у
= yy(t) = y*(t)
является
частным
решением
соответству
ющих
ДИфференциальных
уравнений
(моделей
ВС
или
ВСВ).
Рассмотрим
переход
ные
процессы
в
линейных
динамических
системах,
соответствующие
различным
начальным
значениям
уо
выходной
переменной
y(t),
учитывая,
что
в
общем
случае
уо
i=
у*(О).
Для
устойчивой
(асимптотически)
системы
свободная
составляющая
переходнога
процесса
затухает
(см.
определение
5.1),
т.
е.
выполняется
lim
YCB(t)
=
О.
t->oo
(5.26)
Учитывая
определение
установившейся
составляющей
(см.
2.2.4)
и
условие
(5.26),
запишем
liш
(YB(t)
- y*(t)) =
О
t-oo
и,
следовательно,
lim(y(t)-y*(t))
=
О.
t->oo
,
(5.27)
у
о
t
Рис.
5.4.
Переходные
процессы
(асимптотически)
устойчивой
системы
управления
Последнее
выражение
показывает,
что
выходная
переменная
устойчивой
системы
с
течением
времени
приближается
к
задающему
воздействию
(рис.
5.4)
и,
сле
довательно,
по
окончании
переходнога
процесса
выполняется
требуемое
целевое
условие
(5.24).
