Моклячук М.П., Ямненко Р.Є. Лекції з теорії вибору та прийняття рішень (на укр. языке)
Подождите немного. Документ загружается.

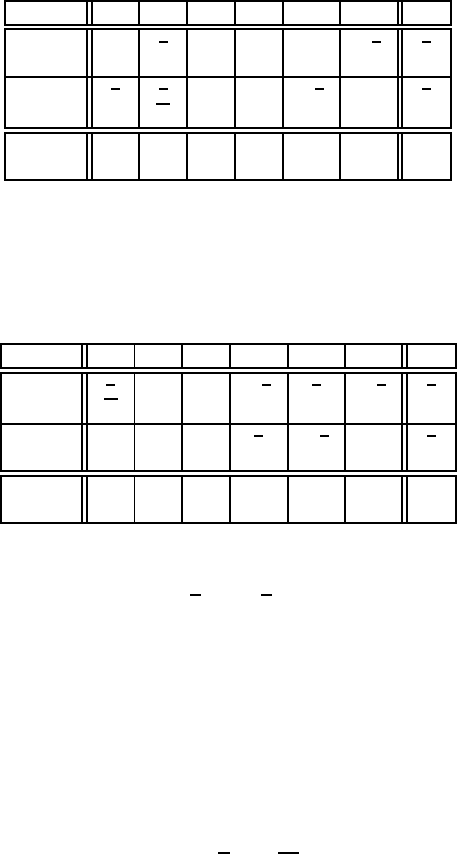
Табл.1.11.1
Базис y
1
y
2
y
3
y
4
y
5
y
6
y
3
1
1
3
1 0 0 −
1
3
5
3
y
4
2
3
2
3
0 1 −
1
3
0
7
3
F
∗
8 4 0 0 −6 −5 67
Складаємо симплекс-таблицю 1.11.1, вибираємо генеральний елемент i
заповнюємо її. Переходимо до симплекс-таблицi 1.11.2, а далi до симп-
лекс-таблицi 1.11.3.
Табл.1.11.2
Базис y
1
y
2
y
3
y
4
y
5
y
6
y
3
2
3
0 1 −
1
2
1
6
−
1
3
1
2
y
2
1 1 0
3
2
−
1
2
0
7
2
F
∗
4 0 0 −6 −4 −5 53
Ми прийшли до оптимального розв’язку двоїстої задачi:
F
∗
min
=50,y
1
=0,y
2
=
7
2
,y
3
=
1
2
,y
4
=0,y
5
=0,y
6
=0,
причому форма F
∗
має наступнi коефiцiєнти при основних змiнних y
1
,
...,
y
4
iдодатковихy
5
, y
6
:
F
∗
min
=50− 0y
1
+0y
2
+6y
3
+3y
4
+5y
5
+3y
6
.
Порiвняємо його зi знайденим у параграфi 1.8.1 оптимальним розв’язком
основної задачi:
F
max
=50,x
1
=5,x
2
=3,x
3
=0,x
4
=0,x
5
=6,x
6
=3,
де форма F має наступнi коефiцiєнти при основних змiнних x
1
, x
2
та
додаткових
x
3
, ..., x
6
:
F =50+0x
1
+0x
2
−
3
4
x
3
−
11
4
x
4
+0x
5
+0x
6
.
Табл.1.11.3
71

Базис y
1
y
2
y
3
y
4
y
5
y
6
y
1
1 0
3
2
−
3
4
1
4
−
1
2
3
4
y
2
0 1 −
3
2
9
4
−
3
4
1
2
11
4
F
∗
0 0 −6 −3 −5 −3 50
Як бачимо, коефiцiєнти функцiї цiлi, що вiдповiдає оптимальному розв’яз-
ку двоїстої задачi, дорiвнюють значенням змiнним оптимального розв’яз-
ку прямої задачi; коефiцiєнти функцiї цiлi, що вiдповiдає оптимальному
розв’язку основної задачi, дорiвнюють значенням змiнним оптимального
розв’язку прямої задачi. Також переконуємось, що
F
max
= F
∗
min
.
Цей взаємозв’язок вiдповiдає наступному спiвставленню основних i
додаткових змiнних прямої та двоїстої задач (див. наслiдок з теоре-
ми 1.10.1):
Змiннi прямої задачi
основнi додатковi
x
1
x
2
y
5
y
6
x
3
x
4
x
5
x
6
y
1
y
2
y
3
y
4
додатковi основнi
Змiннi двоїстої задачi
Таким чином, знаючи розв’язок однiєї задачi, можна, не розв’язуючи,
знайти розв’язок iншої.
1.11.2. Контрольнi запитання i задачi для самостiйної роботи
1. Чи можна побудувати двоїсту задачу для задачi лiнiйного програ-
мування, яка мiстить в системi обмежень нерiвностi рiзного знаку?
2. Яким є зв’язок мiж екстремальними значеннями пари двоїстих за-
дач лiнiйного програмування?
Задачi
Для кожної з наступних задач скласти двоїсту i, розв’язуючи одну з
них, знайти розв’язки обох задач.
72
F
1
=3x
1
+7x
2
→ min ,F
2
=3x
1
− 15x
2
→ min ,
x
1
+5x
2
≥ 0,
3x
1
− x
2
≥ 0,
7x
1
+5x
2
≤ 35,
6x
1
+14x
2
≥ 21,
x
1
≥ 0,x
2
≥ 0;
2x
1
+ x
2
≥ 10,
−x
1
+3x
2
≤ 9,
−x
1
+4x
2
≥ 0,
3x
1
+7x
2
≥ 20,
x
1
≥ 0,x
2
≥ 0;
F
3
=8x
1
+6x
2
+5x
3
→ max ,F
4
=6x
1
+6x
2
+8x
3
→ max ,
10x
1
+9x
2
+15x
3
≤ 1170,
3x
1
+3x
2
+9x
3
≤ 1053,
5x
1
+5x
2
+ x
3
≤ 325,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
15x
1
+9x
2
+10x
3
≤ 1170,
9x
1
+3x
2
+3x
3
≤ 1053,
x
1
+5x
2
+5x
3
≥ 325,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
5
= x
1
− x
2
− 3x
3
→ min ,F
6
=4x
1
+5x
2
+6x
3
→ max ,
4x
1
− 2x
2
+3x
3
≤−2,
2x
1
− x
2
+ x
3
≤ 1,
3x
1
+ x
3
≤ 5,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
2x
1
+3x
2
+4x
3
≥ 80,
2x
1
+3x
2
+6x
3
≤ 240,
2x
1
+ x
2
+2x
3
≤ 100,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
7
=6x
1
+5x
2
+4x
3
→ max ,F
8
= x
1
+7x
2
+6x
3
→ max ,
8x
1
+6x
2
+4x
3
≤ 160,
6x
1
+3x
2
+2x
3
≤ 240,
4x
1
+2x
2
+4x
3
≤ 100,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
x
1
+2x
2
− 3x
3
≤−2,
−3x
1
− 4x
2
+4x
3
≤ 1,
2x
1
− x
2
+3x
3
≤ 6,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
9
=2x
3
→ max ,F
10
= x
3
→ max ,
−x
1
+2x
2
− x
3
≤ 8,
−x
1
+ x
2
+ x
3
≤ 4,
2x
1
− x
2
+4x
3
≤ 10,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
−2x
1
+6x
2
− 7x
3
≥ 10,
−2x
1
+2x
2
− x
3
≤ 2,
3x
1
+ x
2
− 5x
3
≤ 8,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
11
=3x
1
− x
2
→ min ,F
12
=15x
1
+21x
2
→ max ,
2x
1
− 3x
2
≤ 6,
x
1
+2x
2
≤ 13,
−3x
1
+ x
2
≤ 3,
x
1
+3x
2
≥ 3,
x
1
≥ 0,x
2
≥ 0;
−7x
1
+2x
2
≥ 14,
x
1
+11x
2
≤ 13,
x
1
+ x
2
≤ 3,
4x
1
+5x
2
≤ 20,
x
1
≥ 0,x
2
≥ 0;
F
13
= x
1
− x
2
− 3x
3
→ min ,F
14
=6x
1
+5x
2
+9x
3
→ max ,
3x
1
+ x
3
≤ 15,
2x
1
− x
2
+ x
3
≤ 3,
4x
1
− 2x
2
+ x
3
≥−6,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
x
1
+6x
2
+2x
3
≤ 20,
5x
1
+2x
2
+3x
3
≤ 25,
4x
1
+3x
3
≤ 18,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
15
=27x
1
+70x
2
+2x
3
→ min ,F
16
=25x
1
+20x
2
+18x
3
→ min ,
−x
1
+ x
2
≥ 1,
2x
1
+5x
2
+3x
3
≥ 6,
5x
1
+13x
2
− x
3
≥ 1,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
2x
1
+6x
2
≥ 5,
5x
1
+ x
2
+4x
3
≥ 6,
3x
1
+2x
2
+3x
3
≥ 9,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
73
F
17
=2x
1
+3x
2
− x
3
→ min ,F
18
=4x
1
+3x
2
+2x
3
→ max ,
x
1
+2x
2
− x
3
≥ 3,
x
1
+3x
3
≥ 2,
2x
1
− x
2
+2x
3
≥−1,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
10x
1
+5x
2
+2x
3
≤ 200,
5x
1
+5x
2
+6x
3
≤ 300,
5x
1
+8x
2
+4x
3
≤ 400,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
19
=5x
1
+6x
2
+8x
3
→ max ,F
20
=8x
1
+6x
2
+6x
3
→ max ,
x
1
+5x
2
+5x
3
≤ 325,
15x
1
+9x
2
+10x
3
≤ 1170,
9x
1
+3x
2
+3x
3
≤ 1053,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
5x
1
+ x
2
+5x
3
≥ 325,
10x
1
+15x
2
+9x
3
≤ 1170,
3x
1
+9x
2
+3x
3
≤ 1053,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
21
=4x
1
+5x
2
+6x
3
→ max ,F
22
= x
1
+6x
2
+7x
3
→ max ,
2x
1
+ x
2
+2x
3
≤ 50,
2x
1
+3x
2
+4x
3
≤ 80,
2x
1
+3x
2
+6x
3
≤ 240,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
−3x
1
+4x
2
− 4x
3
≤ 1,
x
1
+ −x
2
+2x
3
≤−2,
2x
1
+3x
2
− x
3
≤ 6,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
23
= x
1
− x
2
+3x
3
→ max ,F
24
=3x
1
+5x
2
+2x
3
→ max ,
−x
1
+2x
2
+ x
3
≤ 1,
3x
2
+ x
3
≤ 5,
−2x
1
+4x
2
+3x
3
≤−2,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
x
1
+3x
2
+2x
3
≥ 80,
x
1
+ x
2
+ x
3
≤ 100,
x
1
+3x
2
+3x
3
≤ 240,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
25
=2x
1
→ max ,F
26
= x
2
→ max ,
4x
1
− x
2
+2x
3
≤ 10,
−x
1
+2x
2
− x
3
≤ 8,
x
1
+ x
2
− x
3
≤ 4,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
2x
1
+7x
2
− 6x
3
≤ 10,
2x
1
+ x
2
− 2x
3
≥−2,
3x
1
− 5x
2
+ x
3
≤ 8,
x
1
≥ 0,x
2
≥ 0,x
3
≥ 0;
F
27
= x
1
− 3x
2
→ max ,F
28
=30x
1
+21x
2
→ max ,
−3x
1
+2x
2
≥−6,
2x
1
+ x
2
≤ 13,
x
1
− 3x
2
≤ 3,
3x
1
+ x
2
≥ 3,
x
1
≥ 0,x
2
≥ 0;
7x
1
− x
2
≤−7,
2x
1
+11x
2
≤ 13,
2x
1
+ x
2
≤ 3,
8x
1
+5x
2
≤ 20,
x
1
≥ 0,x
2
≥ 0;
F
29
=6x
1
+7x
2
→ min ,F
30
=6x
1
− 15x
2
→ min ,
12x
1
+14x
2
≥ 21,
2x
1
+5x
2
≥ 0,
6x
1
− x
2
≥ 0,
14x
1
+5x
2
≤ 35,
x
1
≥ 0,x
2
≥ 0;
2x
1
− 4x
2
≥ 0,
4x
1
+ x
2
≥ 10,
2x
1
− 3x
2
≥−9,
6x
1
+7x
2
≥ 20,
x
1
≥ 0,x
2
≥ 0.
74
1.12. ТРАНСПОРТНА ЗАДАЧА ЛIНIЙНОГО
ПРОГРАМУВАННЯ
Cимплекс-метод розв’язування задач лiнiйного програмування є унi-
версальним. Однак серед задач лiнiйного програмування часто зустрiча-
ються такi, якi в силу своєї специфiки допускають розв’язування бiльш
простими методами. Однiєю iз таких задач є транспортна задача лiнiй-
ного програмування.
Загальна постановка транспортної задачi така:
Скласти план перевезень однорiдного вантажу з пунктiв вiдправлення
A
1
,...,A
m
укожномузякийєa
1
,...,a
m
одиниць вантажу вiдповiдно,
у пункти призначення
B
1
,...,B
n
звимогамиb
1
,...,b
n
одиниць вантажу
так, щоб задовольнити вимоги всiх споживачiв i мiнiмiзувати сумарну
вартiсть перевезень. Вартiсть
c
ij
перевезення одиницi вантажу з пункту
вiдправлення
A
i
у пункт призначення B
j
вiдома. При цьому припускає-
ться, що загальний запас вантажу в пунктах вiдправлення (пропозицiя)
дорiвнює сумарнiй вимозi пунктiв споживання (попит), тобто
m
i=1
a
i
=
n
j=1
b
j
. (1.12.1)
Побудуємо математичну модель такої задачi. Нехай
x
ij
–кiлькiсть
вантажу, що вiдправляється з пункту вiдправлення
A
i
у пункт призна-
чення
B
j
. Система змiнних x
ij
повинна задовольняти такi умови:
n
j=1
x
ij
= a
i
,i=1,...,m; (1.12.2)
m
i=1
x
ij
= b
j
,j=1,...,n; (1.12.3)
x
ij
≥ 0,i=1,...,m, j =1,...,n, (1.12.4)
мiнiмiзуючи при цьому сумарну вартiсть перевезень, тобто лiнiйну фор-
му
n
j=1
m
i=1
c
ij
x
ij
. (1.12.5)
Отже, перед нами типова задача лiнiйного програмування iз
m ×n змiн-
ними i
m + n обмеженнями у формi рiвностей. Виявляється, що не всi
n + m рiвнянь задачi є лiнiйно незалежними. Дiйсно, додаючи всi рiвня-
ння (1.12.2) i всi рiвняння (1.12.3), в силу умови (1.12.1) ми одержуємо
те саме. Отже, умови (1.12.2) i (1.12.3) зв’язанi мiж собою однiєю лi-
75

нiйною залежнiстю i невирожденний базисний план транспортної задачi
повинен мiстити
n + m − 1 вiдмiнних вiд нуля компонент.
Теорема 1.12.1. Транспортна задача завжди має розв’язок: для цього
необхiдно i достатньо, щоб виконувалася балансова умова (1.12.1).
Доведення. Необхiднiсть. Якщо задача (1.12.2)–(1.12.5) має розв’язок
x
∗
=(x
∗
11
,...,x
∗
nm
), то система умов (1.12.2)–(1.12.4) задовольняється
ним, а отже, балансова рiвнiсть виконується.
Достатнiсть. Нехай для деякої транспортної задачi виконується ба-
лансове спiввiдношення (1.12.1). Розглянемо величини
x
ij
=
a
i
b
j
d
,
(1.12.6)
де
d =
m
i=1
a
i
=
n
j=1
b
j
=.Неважкопоказати,щоматрицяx
=(x
ij
)
m×n
є
планом задачi (1.12.2)–(1.12.5). Справдi, оскiльки
a
i
> 0, b
j
> 0 та d>0,
то
x
ij
> 0 i, отже, задовольняє природнi обмеження (1.12.4). Крiм того,
за допомогою безпосередньої пiдстановки переконуємось, що величини
x
ij
задовольняють i основнi умови задачi.
Справдi,
m
i=1
x
ij
=
m
i=1
a
i
b
j
d
= b
j
, (1.12.7)
n
j=1
x
ij
=
n
j=1
a
i
b
j
d
= a
i
, (1.12.8)
що й треба було показати.
Отже, транспортна задача завжди має плани перевезення. Покажемо
iснування оптимального плану.
Лема 1.12.1. Лiнiйна форма транспортної задачi обмежена знизу на
множинi планiв задачi.
Доведення. Твердження леми випливає iз обмеженостi многогранника
планiв задачi, так як для кожної змiнної справедливе спiввiдношення
0 ≤ x
ij
≤ min(a
i
; b
j
) (1.12.9)
згiдно з системою умов задачi та невiд’ємностi величин
a
i
, b
j
. Проте
всяка неперервна функцiя, в тому числi i лiнiйна форма задачi, дося-
гає на обмеженiй множинi значень своїх аргументiв свого найменшого
значення.
76

Перед тим, як викласти один iз методiв розв’язування транспортної
задачi, представимо вихiднi данi у видi таблицi, що називається транс-
портною таблицею (таблиця 1.12.1).
Транспортну задачу можна розв’язати тим же методом, яким розв’я-
зувалась задача лiнiйного програмування (замiною базисних i вiльних
змiнних).
Табл.1.12.1
B
1
B
2
··· B
n
a
i
A
1
c
11
c
12
···
c
1n
a
1
A
2
c
21
c
22
···
c
2n
a
2
··· ··· ··· ··· ··· ···
A
m
c
m1
c
m2
···
c
mn
a
m
b
j
b
1
b
2
··· b
n
Розв’язування задачi розпочинається iз знаходження початкового ба-
зисного розв’язку (початкової вершини областi допустимих розв’язкiв).
Для цього використовують рiзнi методи. Опишемо найпростiший iз них,
що називається методом пiвнiчно-захiдного кута.Побудовапочатко-
вого плану перевезень за цим методом розпочинається з лiвого верхньо-
го кута транспортної таблицi. Вантаж першого постачальника розподi-
ляється так, щоб спочатку максимально задовольнити заявку першого
споживача, потiм другого, третього, i так далi, до повного розподiлу
вантажу, який знаходиться у пунктi вiдправлення
A
1
.Потiмтакимже
способом розподiляється вантаж другого постачальника, третього, i так
далi.
Iнший метод – метод найменшої вартостi – починається зi зна-
ходження в транспортнiй таблицi клiтинки з найменшою вартiстю. Цiй
клiтинцi приписується найбiльше значення, допустиме обмеженнями на
попит i пропозицiю. Якщо таких клiтинок декiлька, вибiр є довiльним.
Далi викреслюється вiдповiдний стовпець чи рядок i вiдповiдним чином
коригуються значення пропозицiї та попиту. Якщо одночасно задоволь-
няєтьсяiпропозицiя,iпопит,викреслюєтьсяаборядок,абостовпець.
Потiм з невикреслених клiтинок знову вибирається нова клiтинка з най-
меншою вартiстю i так далi, поки не залишиться лише один невикресле-
ний рядок чи стовпець.
Метод Фогеля є варiацiєю методу найменшої вартостi i в загально-
му випадку знаходить кращий початковий розв’язок. Для кожного ряд-
ка (стовпця), якому вiдповiдає додатна величина пропозицiї (попиту),
77

обчислюється штраф, вiднiмаючи найменшу вартiсть вiд наступної по
величинi у цьому рядку (стовпцi). Визначається рядок чи стовпець iз
найбiльшим штрафом. Якщо ж таких кiлька, довiльним чином вибира-
ється один iз них. З обраного рядка чи стовпця вибирається клiтинка
з найменшою вартiстю, i їй приписується найбiльше значення, допусти-
ме обмеженнями на попит i пропозицiю. Пiсля цього у вiдповiдностi з
приписаним значенням коригуються величини незадоволеного попиту i
нереалiзованої пропозицiї, що залишилися. Рядок або стовпець, що вiд-
повiдає виконаному обмеженню, викреслюється iз таблицi. Якщо одно-
часно виконуються обмеження i на попит, i на пропозицiю, викреслю-
ється тiльки рядок або тiльки стовпець, причому рядку (стовпцю), що
залишився, приписується нульова величина пропозицiї (попиту).
Якщо не викреслено лише один рядок чи стовпець iз нульовим по-
питом чи пропозицiєю, обчислення закiнчуються. Якщо не викреслено
лише один рядок (стовпець) iз додатною пропозицiєю (попитом), в цьому
рядку (стовпцi) методом найменшої вартостi знаходяться базиснi змiннi
i обчислення закiнчуються. Якщо ж усiм невикресленим рядкам i стов-
пцям вiдповiдають нульовi обсяги пропозицiї та попиту, методом наймен-
шої вартостi знаходяться нульовi базиснi змiннi, пiсля чого обчислення
закiнчено. В усiх iнших випадках метод потрiбно повторити спочатку.
Теорема 1.12.2. Для того, щоб деякий план транспортної задачi був
базисним, необхiдно i достатньо його ациклiчностi.
Доведення. Необхiднiсть. Нехай таблиця 1.12.1 мiстить базисний план
транспортної задачi. За означенням, не бiльше
n + m − 1 клiтин будуть
заповненими. Якщо заповнених клiтин буде менш, як
m+n−1,торешта
базисних клiтин знаходиться серед незаповнених.
Вектори умов
ˆa
ij
, що вiдповiдають базисним клiтинам, тобто бази-
сним змiнним, за означенням, лiнiйно незалежнi. Отже, необхiднiсть
умови буде доведено, якщо довести ациклiчнiсть всякого набору клiтин,
що вiдповiдає системi лiнiйно незалежних векторiв умов транспортної
задачi. Зауважимо, що вектор транспортних умов
a
ij
має таку структу-
ру:
m + j
a
ij
=(
0...0
10...01 0...0)
.
i
Припустимо протилежне. Нехай деяка пiдсистема з 2k-векторiв даної
системи базисних векторiв
ˆa
ij
утворює цикл, а саме (i
1
,j
1
)(i
1
,j
2
)(i
2
,j
2
)
(i
2
,j
3
) ...(i
k
,j
1
). Складемо нульову лiнiйну комбiнацiю цих векторiв:
ˆa
11
− ˆa
12
+ˆa
22
− ...− ˆa
k1
=0. (1.12.10)
78
Внаслiдок леми ... i зробленого припущення число членiв лiнiйної комбi-
нацiї має бути парним, тому останнiй член слiд брати зi знаком “мiнус”.
Неважко помiтити, що наведена лiнiйна комбiнацiя справдi дорiвнює
нуль-вектору при прийнятих (вiдмiнних вiд нуля) коефiцiєнтах комбiна-
цiї
λ
11
=1,λ
12
= −1,...,λ
k1
= −1.
Справдi, для пояснення досить зауважити, що кожна i
s
(s =1,2,...,k ≤
m + n − 1)
та m + j
r
(r =1,2,...,k − 1) компоненти базисних векторiв
видiленої пiдсистеми лише в двох випадках (для двох векторiв) вiдмiннi
вiд нуля i дорiвнюють одиницям, причому один з цих векторiв входить
у лiнiйну комбiнацiю (1.12.10) зi знаком “плюс”, а другий – зi знаком
“мiнус”, що й дає в загальнiй сумi нуль-вектор. Проте рiвнiсть (1.12.10)
суперечить умовi лiнiйної незалежностi базисних векторiв, що й дово-
дить необхiднiсть ациклiчностi базисного плану.
Достатнiсть. Нехай деякий план транспортної задачi буде ациклi-
чним. Покажемо, що вiн є базисним. Для цього, очевидно, досить пока-
зати лiнiйну незалежнiсть векторiв умов транспортної задачi, якi вiдпо-
вiдають ненульовим (додатним) компонентам плану.
Позначимо заповненi клiтини плану iндексами
(i
,j
)(i
= i
1
,i
2
,...,i
k
;
j
= j
1
,j
2
,...,j
k
) iвiдповiднiїмвекториумовa
ij
. Множину всiх запов-
нених клiтин
(i
,j
) позначимо H. Доведемо достатнiсть, мiркуючи вiд
супротивного. Нехай вектори
a
ij
лiнiйно залежнi. Розглянемо нульову
лiнiйну комбiнацiю розглядуваних векторiв, маючи на увазi, що деякi з
її коефiцiєнтiв можуть вiдрiзнятися вiд нуля.
(i,j)∈H
λ
ij
a
ij
=0. (1.12.11)
Нехай деяке
λ
i
1
j
1
=0. Перепишемо рiвнiсть (1.12.11) так:
−λ
i
1
j
1
a
i
1
j
1
=
(i,j)∈H
1
λ
ij
a
ij
, (1.12.12)
де
H
1
= H \ (i
1
,j
1
).Оскiлькиi
1
-а компонента в лiвiй частинi рiвностi
(1.12.12) вiдмiнна вiд нуля, то в правiй обов’язково повинен бути хоча б
один доданок з
i-ю компонентою, вiдмiнною вiд нуля, тобто деяке λ
i
1
j
2
=
0
. Перенесемо доданок λ
i
1
j
2
a
i
1
j
2
з правої в лiву частину. Матимемо
−λ
i
1
j
1
a
i
1
j
1
− λ
i
1
j
2
a
i
1
j
2
=
(i,j)∈H
2
λ
ij
a
ij
, (1.12.13)
де
H
2
= H
1
\(i
1
,j
2
).Оскiлькиj
2
= j
1
,iкомпонентаm + j
2
лiвої частини
останньої рiвностi вiдмiнна вiд нуля, то серед доданкiв правої частини
знайдеться хоча б один, для якого коефiцiєнт
λ
i
2
j
2
=0. Перенесемо
79

такожiцейдоданокулiвучастину.Дiстанемо:
−λ
i
1
j
1
a
i
1
j
1
− λ
i
1
j
2
a
i
1
j
2
− λ
i
2
j
2
a
i
2
j
2
=
(i,j)∈H
3
λ
ij
a
ij
, (1.12.14)
де
H
3
= H
2
\ (i
2
,j
2
).
Оскiльки число
N заповнених клiтин, що входять у множину H,а
отже,iчисловекторiв
a
ij
, скiнченне i не перевищує величини m ×
n ≥ N
,точерезN крокiв описаний процес перенесення обов’язково
закiнчиться. Пiсля деякого непарного
2k − 1 чи парного 2k числа крокiв
дiстанемо вiдповiдно такi рiвностi:
−
k
v=1
λ
i
v
j
v
a
i
v
j
v
−
k−1
v=1
λ
i
v
j
v+1
a
i
v
j
v+1
=
(i,j)∈H
2k−1
λ
ij
a
ij
, (1.12.15)
H
2k−1
= H
2k−2
\ (i
k
,j
k
),
−
k
v=1
λ
i
v
j
v
a
i
v
j
v
−
k
v=1
λ
i
v
j
v+1
a
i
v
j
v+1
=
(i,j)∈H
2k
λ
ij
a
ij
, (1.12.16)
H
2k
= H
2k−1
\ (i
k
,j
k+1
).
Розглянемо спiввiдношення (1.12.15). При деякому значеннi k (2 ≤
k ≤
N
2
) серед доданкiв другої суми лiвої частини знайдеться такий, що
має iндекс
i
µ
= i
k
(1 ≤ µ ≤ k − 1). Тодi всi клiтини, що були перенесенi
в лiву частину пiсля
(2µ − 1)-го кроку, утворюють цикл:
(i
µ
,j
µ+1
)(i
µ+1
,j
µ+1
)(i
µ+1
,j
µ+2
) ...(i
k
= i
µ
,j
k
).
Перша та остання клiтина ланцюга мiстяться в одному рядку i тому цикл
очевидний. Разом з тим не можна продовжити i процес перенесення.
Аналогiчнi мiркування, очевидно, стосуються i рiвностi (1.12.16).
Покажемо, що до закiнчення процесу, виходячи з рiвностi (1.12.15),
обов’язково матимемо цикл. Для цього припустимо, що
i
k
= i
µ
(1 ≤
µ ≤ k − 1)
. Тодi, згiдно з попереднiми мiркуваннями, в правiй части-
нi (1.12.15) обов’язково знайдеться доданок з iндексами
(i
k
,j
k+1
),для
якого
λ
i
k
j
k+1
=0, бо iнакше б рiвнiсть (1.12.15) не мала б мiсця. Отже,
процес перенесення у випадку
i
k
= i
µ
завжди можна продовжити, що за-
безпечується необхiднiстю виконання рiвностей (1.12.11)–(1.12.15), яка
випливає з прийнятого припущення про лiнiйну незалежнiсть
a
ij
.
Проте внаслiдок згаданої скiнченностi процесу перенесень (
N ≤ m ×
n
) умова необхiдного виконання рiвностей рiвносильна тому, що випадок
i
k
= i
µ
обов’язково матиме мiсце, а це означатиме побудову циклу.
Отже, припущення лiнiйної незалежностi векторiв
a
ij
∈ H,виражене
в рiвностi (1.12.11), означає, що серед вiдповiдних клiтин iснує цикл, що
суперечить умовi теореми.
80
