Морозов А.В. Домашняя работа по алгебре за 7 класс
Подождите немного. Документ загружается.


121
№966.
а) c
3
+ b
6
= (c + b
2
)(c
2
– cb
2
+ b
4
); б) a
9
– b
6
= (a
3
b
3
)(a
6
+ a
3
b
2
+ b
4
);
в) x
6
– 8 = (x
2
– 2)(x
4
+ 2x
2
+ 4); г) 27 + y
9
= (3 + y
3
)(9 – 3y
3
+ y
6
).
№967.
а) –x
3
+ y
3
= (y – x)(y
2
+ xy + y
2
); б) –8 – p
3
= –(2 + p)(4 – 2p + p
2
);
в) –a
6
+
224
11 11
82 42
aaa
⎛⎞⎛ ⎞
=− + +
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
; г)
6224
1111
27 3 9 3
bbbb
⎛⎞⎛ ⎞
−−=−− − +
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
;
д) c
6
+ 1 = (c
2
+ 1)(c
4
– c
2
+ 1); е) x
6
+ y
6
= (x
2
+ y
2
)(x
4
– x
2
y
2
+ y
4
).
№968.
а) a
3
b
3
–1=(ab–1)(a
2
b
2
+ab + 1); б) 1 + x
3
y
3
= (1 + xy)(1 – xy + x
2
y
2
);
в) 8–a
3
c
3
=(2–ac)(4+2ac + a
2
c
2
); г) m
3
n
3
+27=(mn + 3)(m
2
n
2
– 3mn + 9);
д) x
6
y
3
–c
3
=(x
2
y–c)(x
4
y
2
+cx
2
y+c
2
); е) a
3
–m
3
n
9
=(a–mn
3
)(a
2
+amn
3
+ m
2
n
6
).
№969.
а) 327
3
+ 173
3
= (327 + 173)(327
2
– 327 ⋅ 173 + 173
2
) =
= 500 ⋅ (327
2
– 327 ⋅ 173 + 173
2
) кратно 500;
б) 731
3
– 631
3
= (731 – 631)(731
2
+ 731 ⋅ 631 + 631
2
)=
=100 ⋅ (731
2
+ 731 ⋅ 631 + 631
2
) кратно 100.
№970.
а) 38
3
+37
3
=(38+37)(38
2
–38⋅37+37
2
)=75 ⋅ (38
2
–38 ⋅ 37+37
2
) кратно 75;
б) 99
3
–74
3
=(99–74)(99
2
+99⋅74+74
2
)=25 ⋅ (99
2
+99⋅74+74
2
) кратно 25.
№971.
а) (11с
2
+ a
3
)(–a
3
+ 11c
2
) = 121c
4
– a
6
;
б) (0,8x + y
4
)(–0,8x – y
4
) = –(0,8x + y
4
)
2
= –0,64x
2
– 1,6xy
4
– y
8
;
в) (0,3c–0,2d)(0,2d–0,3c) = –(0,3c – 0,2d)
2
= – 0,09c
2
– 0,12cd – 0,04d
2
;
г) (6x
3
– 4x)(–6x
3
– 4x) = (–4x)
2
– (6x
3
)
2
= 16x
2
– 36x
6
.
№972.
а) x
2
+ 4 – x
2
– 4x – 4 ≠ 0 для любого x;
б) (x – 2)(x + 2) – 4 + x
2
= x
2
– 4 – 4 + x
2
= 2x
2
– 8 ≠ 0 для любого x.
№973.
а) (2x–3)
2
–2x(4+2x)=11, 4x
2
–12x+9–8x–4x
2
= 11, 20x = –2, x = –0,1;
б) (4x–3)(3+4x)–2x(8x–1)=0, 16x
2
–9–16x
2
+2x = 0, 2x = 9, x = 4,5.
§ 14. Преобразование целых выражений
36. Преобразование целого выражения в многочлен
№974. 2x
2
y; 4a
2
– b(a – 3b);
2
1
8
x
−
; 9x –
1
2
.
Не целое
3
2
−a
a
, т.к. есть деление на выражение с переменной.
№975. а) x
3
+ 7x
2
+ 8 + (x
2
– 6x + 4)(x – 1) =
= x
3
+ 7x
2
+ 8 + x
3
– x
2
– 6x
2
+ 6x + 4x – 4 = 2x
3
+ 10x + 4;
б) (a
2
+ 7a – 4)(a – 3) – (a
3
+ 4a
2
– 29a + 11) =
= a
3
– 3a
2
+ 7a
2
– 21a – 4a + 12 – a
3
– 4a
2
+ 29a – 11 = 4a + 1.

122
№976.
а) (5x – 2y)(x + y) – 5x
2
= 5x
2
+ 5xy – 2xy – 2y
2
– 5x
2
= 3xy – 2y
2
;
б) 3a
2
+ (3a + b)(b – a) = 3a
2
+ 3ab – 3a
2
+ b
2
– ab = 2ab + b
2
;
в) 2b(7 – b)–(a+2b)(3–b)=14b – 2b
2
– 3a + ab – 6b + 2b
2
= 8b – 3a + ab;
г) (x+6y)(1–4x)–4x(y–x) = x – 4x
2
+ 6y – 24xy – 4xy + 4x
2
=x + 6y – 28xy;
д) (a + 2b)(4a – 5b) – (3a – b)(b – a) =
= 4a
2
– 5ab + 8ab – 10b
2
– 3ab + 3a
2
+ b
2
– ab = 7a
2
– 9b
2
– ab;
е) (4x – 5y)(3y x) + (2x – y)(x – 2y) =
= 12xy + 4x
2
– 15y
2
– 5xy + 2x
2
– 4xy – xy + 2y
2
= 6x
2
+ 2xy – 13y
2
.
№977. а) 3(x – 4)(x + 2) + (3x – 1)(5 – x) = 3(x
2
– 2x – 8) + 15x – 3x
2
– 5 + x =
= 3x
2
– 6x – 24 + 16x – 3x
2
– 5 = 10x – 29;
б) (b–5)(7–5b)–2(b + 2)(b–6)=7b–5b
2
–35 + 25b – 2b
2
+ 8b+24=–7b
2
+ 40b – 11;
в) (c – 7)(4 + 2c) – 6c(1 – 3c) – (9c – 2)(3 – c) =
= 4c + 2c
2
– 28 – 14c – 6c + 18c
2
– 27c + 9c
2
+ 6 – 2c = 29c
2
– 45c – 22;
г) 5(a + 3)(5 – a) – (a – 8)(1 – a) – 2a(3a – 6) =25a–5a
2
+75 – 15a + a
2
+
+8 – 8a – 6a
2
+ 12a = –10a
2
+ 13a + 75 + 8 = –10a
2
+ 13a + 83;
д) 4(2a+1)(5a–3)–3(a+2)(a+3)=4(10a
2
– 6a + 5a – 3) – 3(a
2
+ 5a + 6) =
= 40a
2
– 24a + 20a – 12 – 3a
2
– 15a – 18 = 37a
2
– 19a – 30;
е) –2(6–3m)(m+1)+5(m–4)(m–5)=–2(6m+6–3m
2
–3m)+5(m
2
– 9m + 20)=
= –12m – 12 + 6m
2
+ 6m + 5m
2
– 45m + 100 = 11m
2
– 51m + 88.
№978.
а) 4(m–n)
2
+4m(m – n) = 4m
2
– 8mn + 4n
2
+ 4m
2
– 4mn=8m
2
–12mn + 4n
2
;
б) 5x(x – y) – 2(y – x)
2
= 5x
2
– 5xy – 2y
2
+ 4xy – 2x
2
= 3x
2
– xy – 2y
2
;
в) (y + 7)
2
– 2(y + 10)(y + 4) = y
2
+ 14y + 49 – 2(y
2
+ 14 + 40) =
= y
2
+ 14y + 49 – 2y
2
– 28y – 80 = –y
2
– 14y – 31;
г) (x – 5)(6 + 4x) – 3(1 – x)
2
= 6x + 4x
2
– 30 – 20x – 3(1 – 2x + x
2
) =
= 6x + 4x
2
– 30 – 20x – 3 + 6x – 3x
2
= x
2
– 8x – 33.
№979. а) (3m – a)(a + 3m) – (2a + m)(3a – m) =
= 3am + 9m
2
– a
2
– 3am – 6a
2
+ 2am – 3am + m
2
= 10m
2
– am – 7a
2
;
б) (x – 4y)(x + 3y) + (x + 3y)(3y + x) =
= x
2
+ 3xy – 4xy – 12y
2
+ 3xy + x
2
– 9y
2
– 3xy = 2x
2
– xy – 21y
2
;
в)
3
2
a(6a+1)(6a–1) – 0,5a
2
22
12
33
a
⎛⎞
+
=
⎜⎟
⎝⎠
a(36a
2
– 1) –
1
2
a
2
2
12
3
a
⎛⎞
+
⎜⎟
⎝⎠
=
= 24a
3
–
2
3
a – 6a
3
–
1
3
a = 18a
3
– a;
г) 0,2b(10c – 5b) – 4(0,5b + 2c)(2c – 0,5b) = 2bc – b
2
– 4(4c
2
– 0,25b
2
) =
= 2bc – b
2
– 16c
2
+ b
2
= 2bc – 16c
2
.
№980.
а) a(1–2a)
2
–(a
2
–2)(2–a)+4a
3
(3a–1)=a(1–4a+4a
2
) – (2a
2
–a
3
–4+2a)+12a
4
– 4a
3
=
=a – 4a
2
+ 4a
3
– 2a
2
+ a
3
+ 4 – 2a + 12a
4
– 4a
3
= 12a
4
+ a
3
– 6a
2
– a + 4;
б) (x
2
– 3x)
2
– x(5 – x)(x + 5) – 5x(2x
3
– 5) = x
4
– 6x
3
+ 9x
2
– x(25 – x
2
) –
–10x
4
+ 25x = –9x
4
– 6x
3
+ 9x
2
+ 25x – 25x + x
3
= –9x
4
– 5x
3
+ 9x
2
.
№981. а) 6x(5x – 24) – 4(3 – 2x)
2
= 30x
2
– 144x – 4(9 – 12x + 4x
2
) =
= 30x
2
– 144x – 36 + 48x – 16x
2
= 14x
2
– 96x – 36;
б) 2y(11y – 9) + 0,5(4y – 3)(4y + 3) = 22y
2
– 18y + 0,5(16y
2
– 9) =
= 22y
2
– 18y + 8y
2
– 4,5 = 30y
2
– 18y – 4,5;

123
в) (a – 3b)(a + 3b) + (2a – 3b)
2
– 4a(b – a) =
= a
2
– 9b
2
+ 4a
2
– 12ab + 9b
2
– 4ab + 4a
2
= 9a
2
– 16ab;
г) (x + 6y)
2
– (6y + 5x)(6y – 5x) + x(12y – 6x) =
= x
2
+ 12xy + 36y
2
– 36y
2
+ 25x
2
+ 12xy – 6x
2
= 20x
2
+ 24xy.
№982.
а)
22 22 4
11 1 1
3313
33 3 9
xx x(x) x
⎛⎞⎛⎞ ⎛⎞
−− ++ −−=−−+
⎜⎟⎜⎟ ⎜⎟
⎝⎠⎝⎠ ⎝⎠
3x
4
– 3x
2
–
1
3
=
= –3x
4
+
1
3
+ 3x
4
– 3x
2
–
1
3
= –3x
2
, при x = –1,5, –3х
2
⋅ (–1,5)
2
= 3 ⋅ 2,25= –6,75;
б) 0,9x ⋅
22 22
22
06 (2 1)
33
xx xx ,x x
⎛⎞⎛⎞
−+−⋅−
⎜⎟⎜⎟
⎝⎠⎝⎠
=
=
22
94
10 9
x
xx
⎛⎞
⋅−
⎜⎟
⎝⎠
– 1,2x
5
+ 0,6x
3
=
5353
2966
510510
x
xx x−−+=
=
5332
43 43
510 510
xxxx
⎛⎞
−− =−⋅ +
⎜⎟
⎝⎠
,
при x = –2,
32
43
510
xx
⎛⎞
−+=
⎜⎟
⎝⎠
–(–2)
3
⋅
43 323 35
48 828
510 1010 10
⎛⎞⎛⎞
⋅
+=⋅+=⋅=
⎜⎟⎜⎟
⎝⎠⎝⎠
.
№983.
а) (a – 1)(a
2
+ 1) (a + 1) – (a
2
– 1)
2
– 2(a
2
– 3) =
= (a
2
–1)(a
2
+1)–(a
4
–2a
2
+1)–2a
2
+ 6 = a
4
– 1 – a
4
+ 2a
2
– 1 – 2a
2
+ 6 = 4;
б) (a
2
– 3)
2
– (a – 2)(a
4
+ 4)(a + 2) – 6(5 – a
2
) =
= a
4
– 6a
2
+ 9 – (a
2
– 4)(a
2
+ 4) – 30 + 6a
2
= a
4
– 21 – a
4
+ 16 = – 5.
№984.
а) (y–3)(y
2
+9)(y+3)–(2y
2
–y)
2
– 19 =(y
2
– 9)(y
2
+ 9)–(4y
4
– 4y
3
+y
2
) – 19 =
= y
4
– 81 – 4y
4
+ 4y
3
– y
2
– 19 = –3y
4
+ 4y
3
– y
2
– 100;
б) (1 – a)(1 – a
2
) + (1 + a)(1 + a
2
) – 2a(1 +a)(a – 1) =
= 1–a
2
–a+a
3
+ 1 + a
2
+ a + a
3
– 2a(a
2
– 1) = 2 + 2a
3
– 2a
3
+ 2a = 2 + 2a.
№985.
а) (a – 3c)(4c + 2a) + 3c(a + 3c) = (2a –c)(3c + 5a) – 8a
2
:
(a–3c)(4c+2a)+3c(a+3c)=4ac+2a
2
–12c
2
–6ac + 3ac + 9c
2
=2a
2
+ ac – 3c
2
(2a–c)(3c+5a)–8a
2
= 6ac + 10a
2
– 3c
2
– 5ac – 8a
2
= 2a
2
+ ac – 3c
2
верно
б) (1 – 2b)(1 – 5b + b
2
) + (2b – 1)(1 – 6b + b
2
) = b(1 – 2b):
(1 – 2b)(1 – 5b + b
2
) + (2b – 1)(1 – 6b + b
2
) =1 – 5b + b
2
– 2b + 10b
2
+
+ 2b – 12b
2
+ 2b
3
– 1 + 6b – b
2
= –2b
2
+ b, b(1 – 2b) = –2b
2
+ b верно.
№986.
а) 25y
2
– 15ay + 9a
2
— нельзя представить;
б)
9
4
b
2
– 0,4bc + 0,09с
2
=
2
2
03
3
b,c
⎛⎞
−
⎜⎟
⎝⎠
;
в) 15ab – 9a
2
–
4
1
6
b
2
= –
2
22
15
915 6 3
42
aabb ab
⎛⎞⎛⎞
−+ =−−
⎜⎟⎜⎟
⎝⎠⎝⎠
;
г) 0,04x
4
– 1,2x
3
+ 0,09х
2
— нельзя представить.
124
№987.
а) –20x
4
y
2
– 35x
3
y
3
= –5x
3
y
2
(4x + 7y);
б) 3a
2
b
2
c + 9ab
2
c
3
= 3ab
2
c(a
2
+ 3c
2
).
№988.
v T S
от деревни до ст. 15 км/ч x ч 15x км равны
от ст. до деревни 10 км/ч (x + 1) ч 10(x + 1) км
15x = 10(x + 1), 15x = 10x + 10, 5x = 10, x = 2 (ч) — время, затраченное ве-
лосипедистом на путь от деревни до станции.
15 ⋅ 2 = 30 км — от деревни до станции.
Ответ: 30 км.
№989.
v t S
из A в B x км/ч
2
1
ч
2
1
км
одинаковое
из B в A (x – 1) км/ч
5
3
ч
5
3
(x – 1) км
2
1
=
5
3
(x – 1),
2
1
x =
5
3
x –
5
3
| ⋅ 10, 5x = 6x – 6,
x = 6 (км/ч) — скорость движения связного из A в B.
Ответ: 6 км/ч.
37. Применение различных способов
для разложения на множители
№990.
а) 5x
2
– 5y
2
= 5(x
2
– y
2
) = 5(x – y)(x + y);
б) am
2
– an
2
= a(m
2
– n
2
) = a(m – n)(m + n);
в) 2ax
2
– 2ay
2
= 2a(x
2
– y
2
) = 2a(x – y)(x + y);
г) 9p
2
– 9 = 9(p
2
– 1) = 9(p – 1)(p + 1);
д) 16x
2
– 4 = 4(4x
2
– 1) = 4(2x – 1)(2x + 1);
е) 75 – 27c
2
= 3(25 – 9c
2
) = 3(5 – c)(5 + c);
ж) 3xy
2
– 27x = 3x(y
2
– 9) = 3x(y – 3)(y + 3);
з) 100ac
2
– 4a = 4a(25c
2
– 1) = 4a(5c – 1)(5c + 1);
и) 50my
2
– 2mx
2
= 2m(25y
2
– x
2
) = 2m(5y – x)(5y + x).
№991.
а) a
3
– a = a(a
2
– 1) = a(a – 1)(a + 1); б) x
2
– x
4
= x
2
(1 –x
2
) = x
2
(1 – x)(1 + x);
в) y
3
–y
5
= y
3
(1–y
2
) = y
3
(1 – y)(1 + y); г) 2x–2x
3
=2x(1–x
2
) = 2x(1 – x)(1 + x);
д) 81x
2
– x
4
= x
2
(81 – x
2
) = x
2
(9 – x)(9 + x);
е) 4y
3
– 100y
5
= 4y
3
(1 – 25y
2
) = 4y
3
(1 – 5y)(1 + 5y).
№992.
а) mx
2
–my
2
=m(x
2
–y
2
)=m(x–y)(x+y); б) ab
2
–4ac
2
=a(b
2
–4c
2
)=a(b – 2c)(b + 2c);
в) 6a
2
–24 =6(a
2
–4)=6(a – 2)(a + 2); г) 7b
2
– 63 = 7(b
2
– 9) = 7(b – 3)(b + 3);
д) 4b
3
–b=b(4b
2
–1)=b(2b – 1)(2b + 1); е) a
3
– ac
2
= a(a
2
– c
2
) = a(a – c)(a + c).
125
№993. a
8
– b
8
= (a
4
)
2
– 9b
4
)
2
= (a
4
– b
4
)(a
4
+ b
4
) = (a
2
– b
2
)(a
2
+ b
2
)(a
4
+ b
4
) =
=(a – b)(a + b)(a
2
+ b
2
)(a
4
+ b
4
).
№994.
а) p
4
– 16 = (p
2
– 4)(p
2
+ 4) = (p – 2)(p + 2)(p
2
+ 4);
б) x
4
– 81 = (x
2
– 9)(x
2
+ 9) = (x – 3)(x + 3)(x
2
+ 9);
в) y
8
–1=(y
4
–1)(y
4
+1)=(y
2
–1)(y
2
+1)(y
4
+1) =(y – 1)(y + 1)(y
2
+ 1)(y
4
+ 1);
г) a
4
– b
8
= (a
2
– b
4
)(a
2
+ b
4
) = (a – b
2
)(a + b
2
)(a
2
+ b
4
).
№995.
а) 3x
2
+ 6xy + 3y
2
= 3(x + y)
2
= 3(х + у)(х + у);
б) –m
2
+ 2m – 1 = –(m
2
– 2m + 1) = –(m – 1)
2
= –(m – 1)(m – 1);
в) –4x – 4 – x
2
= –(x
2
+ 4x + 4) = –(x + 2)
2
= –(x + 2)(x + 2);
г) 6p
2
+24q
2
+ 24 pq = 6(p
2
+ 4pq + 4q
2
) = 6(p + 2q)
2
= 6(p + 2q)(p + 2q);
д) 45x + 30ax + 5a
2
x = 5x(9 + 6ax + a
2
) = 5x(3 + a)
2
= 5x (3 + a)(3 + a);
е) 18cx
2
–24cx+8c = 2c(9x
2
– 12x + 4) = 2c(3x – 2)
2
= 2c(3x – 2)(3x – 2).
№996.
а) 4x
3
– 4y
3
= 4(x
3
– y
3
) = 4(x – y)(x
2
+ xy + y
2
);
б) 7(a
3
+ b
3
) = 7(a + b)(a
2
– ab + b
2
); в) a(m
3
– n
3
) = a(m – n)(m
2
+ mn + n
2
);
г) 16x
3
– 2 = 2(8x
3
– 1) = 2(2x – 1)(4x
2
+ 2x + 1);
д) 1000m + m
4
= m(1000 + m
3
) = m(10 + m)(100 – 10m + m
2
);
е) x
5
– x
2
= x
2
(x
3
– 1) = x
2
(x – 1)(x
2
+ x + 1);
ж) y
3
+ y
6
= y
3
(1 + y
3
) = y
3
(1 + y)(1 + y + y
2
);
з) 27m
2
– m
5
= m
2
(27 – m
3
) = m
2
(3 – m)(9 + 3m + m
2
);
и) 8a
4
– 64a = 8a(a
3
– 8) = 8a(a – 2)(a
2
+ 2a + 4).
№997.
а) (x
6
–y
6
)=(x
3
)
2
–(y
3
)
2
=(x
3
– y
3
)(x
3
+ y
3
)=(x–y)(x
2
+xy+y
2
)(x+y)(x
2
–xy – y
2
);
б) x
6
– y
6
= (x
2
)
3
– (y
2
)
3
= (x
2
– y
2
)(x
4
+ x
2
y
2
+ y
4
)=(x–y)(x+y)(x
4
+x
2
y
2
+ y
2
).
№998.
а) 2m
2
– 4m + 2 = 2(m
2
– 2m + 1) = 2(m – 1)
2
= 2(m – 1)(m – 1);
б) 36 + 24x + 4x
2
= 4(9 + 6x + x
2
) = 4(3 +x)
2
= 4(x + 3)(x + 3);
в) 8a
3
– 8b
3
= 8(a
3
– b
3
) = 8(a – b)(a
2
+ ab + b
2
);
г) 9ax
3
+ 9ay
3
= 9a(x
3
+ y
3
) = 9a(x + y)(x
2
– xy + y
2
).
№999.
а) 4xy + 12y – 4x + 12 = 4y(x + 3) – 4(x – 3) = 4(x + 3)(y – 1);
б) 60+6ab–30b–12a=30(2–b)–6a(2–b) = (30 – 6a)(2–b)=6(5 – a)(2 – b);
в) –abc – 5ac – 4ab – 20a = –ab(c + 4) – 5a(c + 4) =
= (–ab – 5a)(c + 4)= –a(b + 5)(c + 4);
г) a
3
+ a
2
b + a
2
+ ab = a
2
(a + b) + a(a + b) = a(a + 1)(a + b).
№1000.
а) 45b+6a–3ab–90=45(b – 2) – 3a(b –2)=(45–3a)(b–2)=3(15 – a)(b – 2);
б) –5xy–40y–15x–120=–5x(y+3)–40(y+3)=(–5x–40)(y+3)=–5(x+8)(y+3);
в) ac
4
–c
4
+ac
3
–c
3
=c
4
(a–1) + c
3
(a – 1) = (c
4
+ c
3
)(a – 1) = c
3
(c + 1)(a – 1);
г) x
3
–x
2
y + x
2
– xy = x
2
(x – y) + x(x – y) = (x
2
+ x)(x – y) = x(x + 1)(x – y).
№1001.
а) x
2
+ 2xc + c
2
– d
2
= (x – c)
2
– d
2
= (x – c – d)(x – c + d);
б) c
2
+ 2c + 1 – a
2
= (c + 1)
2
– a
2
= (c + 1 – a)(c + 1 + a);
в) p
2
– x
2
+ 6x – 9 = p
2
– (x – 3)
2
= (p – x + 3)(p + x – 3);
г) x
2
– a
2
– 10a – 25 = x
2
– (a + 5)
2
= (x – a – 5)(x + a + 5).
126
№1002.
а) x
2
+ 2xy + y
2
– m
2
= (x + y)
2
– m
2
= (x + y – m)(x + y + m);
б) p
2
– a
2
– 2ab – b
2
= p
2
– (a + b)
2
= (p – a – b)(p + a + b);
в) b
2
– c
2
– 8b + 16 = (b – 4)
2
– c
2
= (b – 4 – c)(b – 4 + c);
г) 9 – c
2
+ a
2
– 6a = (a – 3)
2
– c
2
= (a – 3 – c)(a – 3 + c).
№1003. а) x
2
– y
2
– x – y = (x – y)(x + y) – (x + y) = (x +y)(x – y – 1);
б) a
2
– b
2
– a + b = (a – b)(a + b) – (a – b) = (a – )(a + b – 1);
в) m + n + m
2
– n
2
= (m + n) + (m – n)(m + n) = (1 + m – n)(m + n);
г) k
2
– k – p
2
– p = (k – p)(k + p) – (k + p) = (k + p)(k – p – 1).
№1004. а) a – b + a
2
– b
2
= (a – b) + (a – b)(a + b) = (a – b)(1 + a + b);
б) c
2
+ d – d
2
+ c = (c – d)(c + d) + (c + d) = (c + d)(c – d + 1).
№1005.
а) ab
2
–a–b
3
+b=b
2
(a–b) – (a – b) = (b
2
– 1)(a – b) = (b – 1)(b + 1)(a – b);
б) bx
2
+2b
2
–b
3
–2x
2
=x
2
(b–2)+b
2
(2–b)=(x
2
– b
2
)(b – 2)=(x–b)(x + b)(b – 2);
в) x
3
+x
2
y–4y–4x=x
2
(x+y)–4(x+y)=(x
2
– 4)(x + y) = (x – 2)(x + 2)(x + y);
г) x
3
–3y
2
+3x
2
–xy
2
=x
2
(x+3)–y
2
(x + 3) = (x
2
– y
2
)(x + 3)=(x–y)(x+y)(x + 3).
№1006.
а) x
3
– x = 0, x(x
2
– 1) = 0, x(x – 1)(x + 1) = 0, x
1
= 0; x
2
= 1; x
3
= –1;
б) 9x – x
3
= 0, x(9 – x
2
) = 0, x(3 – x)(3 + x) = 0, x
1
= 0; x
2
= 3; x
3
= –3;
в) x
3
+ x
2
= 0, x
2
(x + 1) = 0, x
1
= 0; x
2
= –1;
г) 5x
4
–20x
2
=0, 5x
2
(x
2
–4)=0, 5x
2
(x – 2)(x + 2) = 0, x
1
=0; x
2
=2; x
3
=–2.
№1007.
а) x
3
+ x = 0, x(x
2
+ 1) = 0, x
1
= 0; больше нет, т.к. x
2
+ 1 ≠ 0 для любого x;
б) x
3
– 2x
2
= 0, x
2
(x – 2) = 0, x
1
= 0; x
2
= 2.
№1008.
x
3
– x = x(x
2
– 1) = x(x– 1)(x + 1).
Выражение делится на 6, т.к. хотя бы одно из x, x + 1, x + 2 четно и одно де-
лится на 3.
№1009.
Если 2a – 1, 2a + 1 — два последовательных нечетных числа, то
(2a + 1)
2
– (2a – 1)
2
= (2a + 1 – 2a + 1)(2a + 1 + 2a – 1) = 2(4a) = 8a
кратно 8.
№1010.
а) (6x–1)(6x+1) – (12x – 5)(3x + 1) = 36x
2
– 1 – (36x
2
+ 12x – 15x – 5) =
= 36x
2
– 1– 36x
2
+ 3x + 5 = 3x + 4, при x=0,2, 3x+4=3 ⋅ 0,2 + 4 = 4,6;
б) (5+2x)
2
–2,5x(8x+7)=25 + 20x + 4x
2
– 20x
2
– 17,5x=–16x
2
+ 2,5x + 25,
при x = –0,5, –16x
2
+ 2,5x + 25 = –16 ⋅ 0,25 + 2,5 ⋅ (–0,5) + 25 = 19,75.
№1011. y = 0,02x
2
;
а) A(15; 4,5) 0,02 ⋅ 15
2
= 4,5 ⇒ A ∈ графику;
б) B(–2,05; –0,12) 0,02 ⋅ (–2,02)
2
= 0,08405 ≠ –0,12 ⇒ B ∉ графику;
в) C(50; 50) 0,02 ⋅ 50
2
= 50 ⇒ C ∈ графику.
№1012. y = 0,24x + 6;
Т.к. график функции пересекается с Ox, то y = 0,
0,24x + 6 = 0, 0,24x = –6, x = 25, A(25; 0);
Т.к. график функции пересекается с Oy, то x = 0,
y = 0,24 ⋅ 0 + 6, y = 6, B(0; 6).
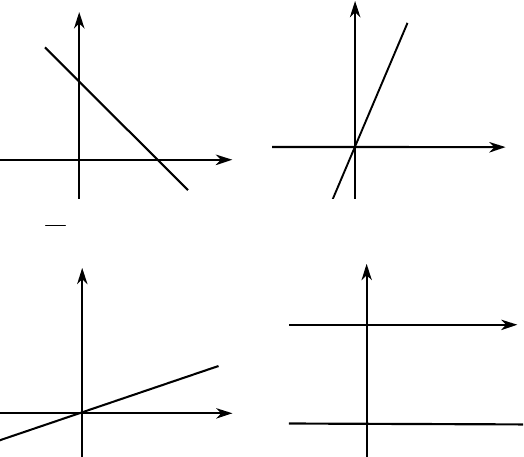
127
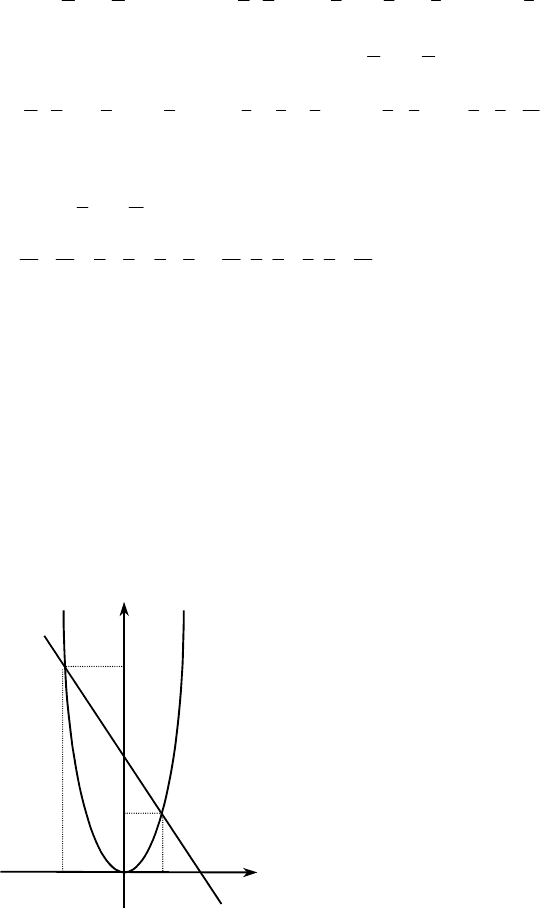
№1013.
а) y = –0,9x + 4. б) y = 2,3x.
4
x
y
0
x
y
0
в) y =
10
x
. г) y = –9.
x
y
0
–
9
y
x
0
38. Применение преобразований целых выражений
№1014.
а) x
2
+2x+2 = (x
2
+ 2x + 1) + 1 = (x + 1)
2
+ 1 > 0, т.к. (x + 1)
2
≥ 0, 1 > 0;
б) 4x
2
–4x+6=(4x
2
–4x+1) + 5 = (2x – 1)
2
+ 5 > 0, т.к. (2x – 1)
2
≥ 0, 5>0;
в) a
2
+ b
2
– 2ab + 1 = (a – b)
2
+ 1 > 0, т.к. (a – b)
2
≥ 0, 1 > 0;
г) x
2
+ y
2
+ z
2
+ 2xy + 5 = (x
2
+ 2xy + y
2
) + z
2
+ 5 = (x + y)
2
+ z
2
+ 5 > 0,
т.к. (x + y)
2
≥ 0, z
2
≥ 0, 5 > 0.
№1015. 2b–b
2
–2 = –(b
2
–2b+1) – 1 = –(b – 1)
2
– 1 < 0, т.к. (b – 1)
2
≥ 0, –1 < 0.
№1016. а) y
2
–10y+30 = y
2
–10y + 25 + 5=(y – 5)
2
+ 5>0, т.к. (y – 5)
2
≥ 0, 5 > 0;
б) c
2
+ 4cd + 4d
2
+ 4 = (c + 2d)
2
+ 4 > 0, т.к. (c + 2d)
2
≥ 0, 4 > 0.
№1017.
Пусть 2k + 1 — нечетное число.
(2k + 1)
2
= 4k
2
+ 4k + 1, 4k
2
+ 4k четное, 4k
2
+ 4k + 1 нечетное.
№1018.
(2n + 10)(n + 5) – 2(n + 3)(n – 3) – (5n + 13) =
= 2n
2
+ 10n + n + 5 – 2n
2
+ 18 – 5n – 13 = 6n – 10.
Т.к. 6n кратно 6, а 10 на 6 без остатка не делится, то и исходное число не
кратно 6.
№1019. (n+8)(n–4)–(n+3)(n – 2) + 27 = n
2
+ 4n – 32 – n
2
– n + 6 + 27 = 3n + 1.
Т.к. 3n кратно 3, а 1 не кратна 3, то и исходное число не кратно 3.
128
№1020. а) 3a
2
b + 2ab
2
= ab(3a + 2b),
при a=–
3
2
, b=
2
1
, ab(3a+2b)=–
2
3
⋅
1
2
⋅
211 1
32 (21)
323 3
⎛⎞
⎛⎞
⋅
−+⋅=−⋅−+=
⎜⎟
⎜⎟
⎝⎠
⎝⎠
;
б) 2mn
2
– 3m
2
n + 1 = mn(2n – 3m) + 1, при m = –
2
1
, n =
3
2
, mn(2n – 3m) + 1 =
= –
2
1
⋅
2
3
⋅
21 111
23 1 111
32 332
⎛⎞
⎛⎞ ⎛ ⎞
⋅−⋅− +=−⋅ + +
⎜⎟
⎜⎟ ⎜ ⎟
⎝⎠ ⎝ ⎠
⎝⎠
41 41 1
1
92 9218
=− − + =− + =
.
№1021. (a
2
+ b
2
)(a + b)(a – b) = (a
2
+ b
2
)(a
2
– b
2
) = a
4
– b
4
;
а) при a = 2, b = 0,1, удобнее использовать a
4
–b
4
=2
4
–(0,1)
4
= 15,9999;
б) при a =
3
4
, b =
11
4
, удобнее использовать (a
2
+ b
2
)(a + b)(a – b) =
=
9131311042515
16 16 4 4 4 4 4 4 4 8 2 16
⎛⎞⎛⎞⎛⎞
++−=⋅⋅=⋅=
⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠
.
1022. Для вычислений на калькуляторе удобнее использовать формулу
x(a + b – c). Вычислим: при a = 3,17; b = 1,12; c = 0,97; x = 4,11,
x(a + b – c) = 4,11(3,17 + 1,12 – 0,97) = 13,6452.
№1023.
при x = 3,7, 3,5x
3
–2,1x
2
+1,9x–16,7=3,5⋅3,7
3
–2,1⋅3,7
2
+1,9⋅3,7–16,7 = 138,8665.
№1024. x
4
– 20x
3
– 19x
2
– 32x + 40 = x
4
– 20x
3
– 20x
2
+ x – 40x + 8x + 40 =
= x
4
–20x
2
(x+1)–40(x–1)+x(x+8)=x
2
(x
2
–20(x+1))–40(x–1)+x(x + 8), при x = 21;
x
2
(x
2
– 20(x + 1)) – 40(x – 1) + x(x + 8), 21
2
(21
2
– (21 – 10)(21 + 1)) –
– 40 ⋅ 20 + 21 ⋅ 29 = 21
2
– 21
2
+ 1 – 800 + 21 ⋅ 29 = 21(21 + 29) – 800 =
= 21 ⋅ 500 – 800 = 1050 – 800 = 250.
№1025. y = 4(3 – 2x) – 5; y = 12 – 8x – 5; y = –8x + 7 — линейная;
y = x – 8(x – 8); y = x – 8x + 64; y = –7x + 64 — линейная;
–8x + 7 = –7x + 64, –x = 57, x = –57, y = –8(–57) + 7 = 463.
Точка пересечения графиков (–57; 463).
№1026. y = x
2
; y = –x + 6.
L
4
x
y
0
6
9
2
–
3
Ответ: (2; 4) и (–3; 9).

129
№1027.
а) a
2
+ b
2
– c
2
+ 2ab = (a +b )
2
– c
2
= (a + b + c)(a + b – c);
б) m
2
– x
2
– y
2
+ 2xy = m
2
– (x – y)
2
= (m –x + y)(m + x – y);
в) a
3
+ a
2
– ab
2
– b
2
=a(a
2
– b
2
) + (a
2
– b
2
)=(a + 1)(a
2
– b
2
)=(a + 1)(a – b)(a + b);
г) 9n+m
3
–m
2
n – 9m = 9(n – m) – m
2
(n – m) = (n – m)(9 – m
2
)=(n–m)(3–m)(3+m).
Дополнительные упражнения к главе V
К параграфу 12
№1028.
а)
2
11
9
39
x
⎛⎞
+
=
⎜⎟
⎝⎠
x
2
+ 6x + 81; б)
2
525
3
636
y
⎛⎞
−=
⎜⎟
⎝⎠
y
2
– 5y + 9;
в)
2
1
2
2
ab
⎛⎞
−+
⎜⎟
⎝⎠
= 4a
2
– 2ab +
4
1
b
2
; г)
2
1
3
3
x
y
⎛⎞
−−
⎜⎟
⎝⎠
= 9x
2
+ 2xy +
9
1
y
2
;
д) (5xy – 0,8y
2
)
2
= 25x
2
y
2
– 8xy
3
+ 0,64y
4
;
е) (0,4a + 10ab)
2
= 0,16a
2
+ 8a
2
b + 100a
2
b
2
;
ж) (3a
2
–5ab)
2
=9a
4
–30a
3
b+25a
2
b
2
; з) (8xy+3y
2
)
2
= 64x
2
y
2
+ 48xy
3
+ 9y
4
;
и) (a
3
b
3
– 1)
2
= a
6
b
6
– 2a
3
b
3
+ 1; к) (2 + x
4
y
2
)
2
= 4 + 4x
4
y
2
+ x
8
y
4
;
л) (x
6
– 3xy
2
)
2
= x
12
– 6x
7
y
2
+ 9x
2
y
4
; м) (y
8
– 2x
4
y)
2
= y
16
– 4x
4
y
+ 4x
8
y
2
.
№1029.
а) (0,7x
3
y – 2xy
3
)
2
= 0,49x
6
y
2
– 2,8x
4
y
4
+ 4x
2
y
6
;
б)
2
33
32 9
43 16
ab ab
⎛⎞
−=
⎜⎟
⎝⎠
a
6
b
2
– a
4
b
4
+
9
4
a
2
b
6
;
в) (0,2p
3
q + 0,3pq
3
)
2
= 0,04p
6
q
2
+ 0,12p
4
q
4
+ 0,09p
2
q
6
;
г)
2
423 2837 46
18 1 2 64
89 64 9 81
bc bc bc bc bc
⎛⎞
+=++
⎜⎟
⎝⎠
.
№1030.
а) (2m
3
n + 0,3mn
4
)
2
= 4m
6
n
2
+ 1,2m
4
n
5
+ 0,09m
2
n
8
;
б)
2
42 84 53 22
13 12 9
35 9525
ab ab ab ab ab
⎛⎞
−=−+
⎜⎟
⎝⎠
;
в) (0,1a
6
b + 0,2ab
6
)
2
= 0,01a
12
b
2
+ 0,04a
7
b
7
+ 0,04a
2
b
12
;
г)
2
52 6 104 68 212
13 1 1 9
64 36 416
x
yxy xyxy xy
⎛⎞
−= −+
⎜⎟
⎝⎠
.
№1031.
(a + b + c)
2
= ((a + b) + c)
2
= (a + b)
2
+ 2(a + b)c + c
2
=
= a
2
+ 2ab + b
2
+ 2ac + 2bc + c
2
= a
2
+ b
2
+ c
2
+ 2ab + 2ac + 2bc.
№1032.
а) (a + b)
4
= ((a + b)
2
)
2
= (a
2
+ 2ab + b
2
)
2
=
= a
4
+ 4a
2
b
2
+ b
4
+ 4a
3
b + 4ab
3
+ 2a
2
b
2
= a
4
+ 4a
3
b + 6a
2
b
2
+ 4ab
3
+ b
4
;
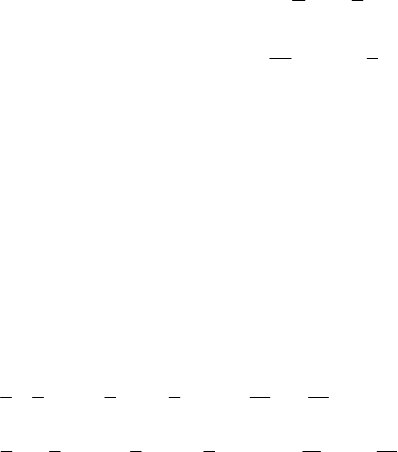
130
б) (a – b)
4
= ((a – b)
2
)
2
= (a
2
– 2ab + b
2
)
2
=
= a
4
+ 4a
2
b
2
+ b
4
– 4a
3
b – 4ab
3
+ 2a
2
b
2
= a
4
– 4a
3
b + 6a
2
b
2
– 4ab
3
+ b
4
.
№1033.
а) (x + 7)
2
– (x – 5)(x + 19) = x
2
+ 14x + 49 – x
2
– 14x + 95 = 144;
б) (x + 9)
2
+ (8 – x)(x + 26) = x
2
+ 18x + 81 + 8x + 208 – x
2
– 26x = 289.
№1034.
а) b
2
+ 10b + 25 = (b + 5)
2
; б) c
2
– 8c + 16 = (c – 4)
2
;
в) 16x
2
– 8x + 1 = (4x – 1)
2
; г) 4c
2
+ 12c + 9 = (2c + 3)
2
;
д) x
4
+ 2x
2
y
+ y
2
= (x
2
+ y)
2
; е) a
6
– 6a
3
b
2
+ 9b
4
= (a
3
– 3b
2
)
2
.
№1035.
а) a
4
– 8a
2
+ 16 = (a
2
– 4)
2
; б) –4 – 4b – b
2
= –(b + 2)
2
;
в) 10x – x
2
– 25 = –(x – 5)
2
; г) c
4
d
2
+ 1 – 2c
2
d = (c
2
d – 1)
2
;
д) a
6
b
2
+ 12a
3
b + 36 = (a
3
b + 6)
2
; е) x + 1 +
4
1
x
2
=
2
1
1
2
x
⎛⎞
+
⎜⎟
⎝⎠
;
ж) y – y
2
– 0,25 = –(y – 0,5)
2
; з) 9 – m +
36
1
m
2
=
2
1
3
6
m
⎛⎞
−
⎜⎟
⎝⎠
;
и) –25 – 2n – 0,04n
2
= –(5 + 0,2n)
2
.
К параграфу 13
№1036.
а) (x
2
– 11)(11 + x
2
) = x
4
– 121; б) (y
2
+ 10)(–10 + y
2
) = y
4
– 100;
в) (a
5
– 1)(a
5
+ 1) = a
10
– 1; г) (b
7
+ 3)(–b
7
+ 3) = 9 – b
14
;
д) (–c
6
– 8)(c
6
– 8) = 64 – c
12
; е) (d
9
– 5)(–5 – d
9
) = 25 – d
18
.
№1037.
а) 1005 ⋅ 995 = (1000 + 5)(1000 – 5) = 1000000 – 25 = 999975;
б) 108 ⋅ 92 = (100 + 8)(100 – 8) = 10000 – 64 = 9936;
в) 0,94 ⋅ 1,06 = (1 – 0,06)(1 + 0,06) = 1 – 0,0036 = 0,9964;
г) 1,09 ⋅ 0,91 = (1 + 0,09)(1 – 0,09) = 1 – 0,0081 = 0,9919;
д)
16 1 1 1 48
10 9 10 10 100 99
77 7 7 49 49
⎛⎞⎛⎞
⋅= + −= −=
⎜⎟⎜⎟
⎝⎠⎝⎠
;
е)
72 2 2 4 77
99 100 100 100 10000 9999
99 9 9 81 81
⎛⎞⎛⎞
⋅=− += −=
⎜⎟⎜⎟
⎝⎠⎝⎠
.
№1038.
а) 5y(y
2
– 3)(y
2
+ 3) = 5y(y
4
– 9) = 5y
5
– 45y;
б) –8x(4x – x
3
)(4x + x
3
) = –8x(16x
2
– x
6
) = – 128x
3
+ 8x
7
;
в) (a
4
– 3)(a
4
+ 3)(a
8
+ 9) = (a
8
– 9)(a
8
+ 9) = a
16
– 81;
г) (1 – b
3
)(1 + b
3
)(1 + b
6
) = (1 – b
6
)(1 + b
6
) = 1 – b
12
.
№1039.
а) (a + 2)(a – 2) – a(a – 5) = a
2
– 4 – a
2
+ 5a = 5a – 4;
б) (a – 3)(3 + a) + a(7 – a) =a
2
– 9 + 7a – a
2
= 7a – 9;
в) (b – 4)(b 4) – (b – 3)(b + 5) = b
2
– 16 – b
2
– 2b + 15 = –1 – 2b;
г) (b + 8)(b – 6) – (b – 7)(b + 7) = b
2
+ 2b – 48 – b
2
+ 49 = 2b + 1;
