Москвин Б.В. Теория принятия решений
Подождите немного. Документ загружается.

111
∃(α,β) ∈ Q, (V
β
- U
α
) > c
αβ
, (6.11)
то перевозку K = (α,β) целесообразно ввести в число базисных,
тогда x
αβ
> 0. Однако, в базисе S (соответственно, в опорном ре-
шении) не может содержаться более (m+n-1) переменных, тогда
некоторую перевозку R = (γ,δ) следует вывести из базиса S.
Алгоритм решения транспортной задачи, основанный на
методе потенциалов, представляет собой итерационный алго-
ритм [45]. На каждой итерации выполняются три шага:
a). Проверяется условие (6.10) и, если оно выполняется, то те-
кущее
решение оптимально. Если (6.10) не выполняется, то вы-
бирается перевозка K=(α,β), которая вводится в число базисных.
б). Выявляется перевозка R=(γ,δ), которую следует вывести из
базиса.
в). Производится пересчет текущего базисного решения, и вы-
числяется значение целевой функции.
Рассмотрим содержание описанных шагов.
a). Анализ оптимальности текущего решения. Определе-
ние перевозки, вводимой в базис.
♦ Вычисляются потенциалы U
i
, V
j
из системы уравнений
V
j
- U
i
- c
ij
= 0, ∀(i,j) ∈ S,
причем U
1
= const, например, U
1
= 0.
♦ Рассчитывается невязка
η(α,β) = max (V
j
- U
i
- c
ij
).
(i,j)∈Q
Если η(α,β) ≤ 0, то решение оптимально.
Если η(α,β) > 0, то перевозку K = (α,β) целесообразно ввести
в базис S.
б). Нахождение перевозки, выводимой из базиса.
Строится ε-маршрут. Для некоторого базиса S запланиро-
ванные перевозки характеризуются графом.
Например,
S = {(1,1),(1,2),(2,2),(3,3),... } 1 2 3 . . . . . m
Пусть K = (2,1), тогда
O O O O
ε-маршрут имеет вид
ε: (2,1)-(1,1)-(1,2)-(2,2).
O O O O O
1 2 3 4 . . . . . n
Т.е. для того, чтобы произвести перевозку (2,1), необходимо из-
менить перевозки (1,1), (1,2), (2,2). Причем те перевозки, которые
112
в ε-маршруте проходятся в прямом направлении, должны быть
увеличены на величину ε, те же перевозки, которые проходятся в
обратном направлении, должны быть уменьшены на ε. Тогда
ε: (2,1)-(1,1)-(1,2)-(2,2).
+ - + -
В качестве ε берется минимальное значение из тех пере-
возок, которые должны быть сокращены. Т.е.
ε = min x
-
ij
, (i,j) ∈ S
Перевозка R = (γ,δ), на которой достигается ε, будет равна 0, т.е.
фактически она выводится из базиса S.
в). Пересчет опорного решения.
♦ Новый базис S′ вычисляется как
S′ = S ∪ K \ R.
♦ В новом опорном решении x′ изменяется значение перевозок
на ε-маршруте по правилу
x
ij
′
-
= x
ij
-
- ε
x
ij
′
+
= x
ij
+
+ ε
♦ Вычисляется новое значение целевой функции
L(x′) = L(x) - ηε.
Все данные результатов счета на каждой итерации пред-
ставляются в таблице вида
V
j
U
i
V
1
……… V
n
U
1
c
11
x
11
………
c
1n
x
1n
a
1
…… ……
c
ij
x
ij
…… ……
U
m
c
m1
x
m1
………
c
mn
x
mn
a
m
b
1
……… b
n
a
i
b
j
Рассмотрим пример из п.6.1.1. Возьмем в качестве исход-
ного опорного решения решение, полученное методом наимень-
шего элемента. η(i,j) = V
j
- U
i
- c
ij
113
Итерация 1.
а).
♦Вычисляются потенциалы
V
j
- U
i
- c
ij
= 0, ∀(i,j) ∈ S,
♦Рассчитываются невязки
η(i,j) = V
j
-U
i
-c
ij
для (i,j)∈Q
η(1,1)= -1; η(3,1)= -4;
η(2,3)= -4; η(3,2)= 1;
η(2,4)=-10; η(3,4)= -3;
η = 1; K = (3,2);
б). Строится ε-маршрут
1 2 3
О О О ε: (3,2)-(1,2)-(1,3)-(3,3)
+ - + -
ε = min {3, 8} = 3; R = (1,2).
О О О О
1 2 3 4
в). Производится пересчет таблицы.
x
32
-
= 3; x
12
-
= 0; x
13
-
= 4; x
33
-
= 5;
L = 92 - 1×3 = 89 .
Итерация 2.
а).
♦Вычисляются потенциалы
V
j
- U
i
- c
ij
= 0, ∀(i,j) ∈ S,
♦Рассчитываются невязки
η(i,j) = V
j
-U
i
-c
ij
для (i,j)∈Q
η(1,1)= -2; η(2,4)= -9;
η(1,2)= -1; η(3,1)= -5;
η(2,3)= -3; η(3,4)= -3;
η = -1;
- решение оптимально.
x
13
-
= 4; x
14
-
= 7; x
21
-
= 5; x
22
-
= 6; x
32
-
= 3; x
33
-
= 5; L = 89 .
Отметим, что если в качестве исходного опорного решения
использовать план, полученный методом северо-западного угла
(см.6.1.1), то в этом случае, то же самое оптимальное решение
будет получено на пятой итерации метода потенциалов.
V
j
U
i
6 8 5 3
0
7
8
3-
5
1+
3
7
11
4
2
5
4
6
5
9
11
4
6
3
ε
1
8-
2
8
5 9 9 7
a
i
b
j
V
j
U
i
5 7 5 3
0
7
8
5
4
3
7
11
3
2
5
4
6
5
9
11
4
6
3
3
1
5
2
8
5 9 9 7
a
i
b
j
114
6.2. Транспортная задача в сетевой постановке
Пусть имеется множество A пунктов производства, транс-
портировки и потребления, соединенных транспортной сетью до-
рог (участками пути)
A = A
p
∪ A
t
∪ A
k
,
здесь
A
p
- множество пунктов производства продукции;
A
t
- множество пунктов транспортировки продукции;
A
k
- множество пунктов потребления продукции;
Если имеется всего n пунктов (узлов) транспортной сети, то
A = {A
1
,..., A
n
} = { A
i
, i∈I} , здесь I = {1,2,..., n}.
Тогда и множество номеров пунктов I можно представить в виде
I = I
p
∪ I
t
∪ I
k
,
где
I
p
= {P
1
,...,P
p
}; I
t
= {T
1
,...,T
t
}; I
k
= {K
1
,...,K
k
}, n = p + t + k.
На множестве пунктов (узлов) A строится транспортная
сеть Г, которая задается
Г = (A, E, C),
где
Е ⊆ A × A - множество дуг графа транспортной сети (задает
возможные перевозки);
Е = {(A
i
, A
j
), i,j ∈ I} = {e
q
, q=1,...,z },
то есть e
q
= (A
i
, A
j
) и │E│ = z;
C: E → R
1
– функция, описывающая качество перевозок.
Обозначим множество возможных перевозок через J, тогда
J = { (i,j) │(A
i
, A
j
) ∈ E}
Каждому пункту A
i
сопоставляется величина потребления продук-
ции a
i
, причем, если A
i
∈ A
p
, то a
i
> 0
если A
i
∈ A
k
, то a
i
< 0
если A
i
∈ A
t
, то a
i
= 0.
Далее будем полагать, что
∑
=
n
1i
a
i
= 0. Если это условие не выпол-
няется, то его можно обеспечить путем введения фиктивного
пункта производства (или потребления).
В этих условиях необходимо найти план, минимизирующий
суммарную стоимость перевозок.
Для математической постановки задачи необходимо, преж-
де всего, определить конструкцию, которой будет описываться
115
решение (план перевозок). По аналогии, как и в ситуации класси-
ческой транспортной задачи (см. 6.1), план перевозок будем опи-
сывать вектором x
x =
║x
ij
. (i,j) ∈ J║. (6.12)
Компоненты x
ij
характеризуют объем перевозок из узла A
i
в узел
A
j
. Ограничения на возможные перевозки накладываются струк-
турой транспортной сети, объемом продукции, имеющейся на
пунктах производства, и объемом продукции необходимой пунк-
там потребления. Целевая функция характеризует суммарные
расходы на все такие перевозки.
Обозначим через I
i
-
- множество узлов сети (пунктов), в ко-
торые могут осуществляться перевозки из i-го узла; соответст-
венно, I
i
+
- множество узлов сети, из которых могут осуществлять-
ся перевозки в i-ый узел;
I
i
-
=
{ j∈I│(i,j) ∈ J} = { j∈I│(A
i
, A
j
) ∈ E}, (6.13)
I
i
+
=
{ j∈I│(j,i) ∈ J} = { j∈I│(A
j
, A
i
) ∈ E}. (6.14)
Так например, если фрагмент транспортной сети имеет вид
5 О О1
О О4
8 О i О9
то I
i
-
=
{1, 4, 9}; I
i
+
=
{5, 8}.
Тогда математическая модель транспортной задачи в сете-
вой постановке имеет вид:
∑
∈J)j,i(
c
ij
x
ij
→ min (6.15)
при ограничениях
Σ x
ij
- Σ x
ji
= a
i
, i = 1,…, n, (6.16)
j∈I
i
-
j∈I
i
+
x
ij
≥ 0, (i,j) ∈ J. (6.17)
Число ограничений такой задачи равно числу узлов транс-
портной сети (n), а число переменных равно числу дуг графа се-
ти (z). Задача (6.15)-(6.17) относится к классу задач линейного
программирования и может решаться с использованием стан-
дартных методов. Однако для решения такой задачи был разра-
ботан модифицированный метод потенциалов, учитывающий ее
специфику.
Введем некоторые понятия и дадим определения, которые
будут использоваться в дальнейшем при изложении алгоритмов.

116
♦ П у т е м W
ij
из узла i в узел j транспортной сети будем на-
зывать упорядоченную последовательность перевозок таких, что
конец одной из них является началом другой
W
ij
=
{ (i,j
1
), (j
1
,j
2
) , (j
2
,j
3
) ,…, (j
k-1
,j)},
количество элементов (k) в этой последовательности называется
д л и н о й п у т и; │W
ij
│= k.
Каждому пути W
ij
может быть поставлена в соответствие
стоимость перевозок С(W
ij
) по этому пути
С(W
ij
) = Σ с
rs
x
rs
(r,s)∈W
ij
♦ Путем м и н и м а л ь н о й стоимости из узла i в узел j бу-
дем называть путь, W
*
ij
такой, что
W
*
ij
= arg min С(W
ij
)
{W
ij
}
С(W
*
ij
) – минимальная стоимость перевозок из узла i в узел j.
Метод потенциалов позволяет оценить оптимальность те-
кущего плана перевозок и, если план не является оптимальным,
то позволяет определить пути улучшения такого плана. Таким
образом, для начала работы алгоритма необходимо найти исход-
ный опорный план.
Построение опорного плана.
Рассмотрим модификацию метода минимального элемента
применительно к транспортной задаче в сетевой постановке.
0). Исходное состояние: номер итерации k = 1;
А
1
= (А
1
1
,...,А
1
n
), A
1
i
= │a
i
│, i ∈ I;
в качестве текущего пути (i,j) выбирается путь минимальной
стоимости
W
ij
= arg min С(W
rs
),
r∈I
p
s∈I
k
здесь I
p
- множество номеров пунктов производства продукции;
I
k
- множество номеров пунктов потребления продукции.
Каждая k-я итерация состоит в выполнении 3-х шагов:
а). Пересчитывается объем перевозок по пути W
ij
g
ij
= min {A
k
i
, A
k
j
} ,
x
′
rs
= x
rs
+ g
ij
, (r,s) ∈ W
ij
Пересчитываются значения компонент вектора A :
A
i
k+1
= A
k
i
- g
ij
;
A
j
k+1
= A
k
j
- g
ij
.
117
б).
Если A
i
k+1
= 0, i∈I, то процесс окончен, т.е. все ресурсы по-
ставщиков исчерпаны, и все запросы потребителей удовлетворе-
ны. Если это не так, то определяется очередной путь:
W
ij
= arg m i n С(W
rs
)
r∈I
p
│A
r
k+1
>0
s∈I
k
│A
s
k+1
>0
в). k = k+1. Переход на шаг а.
Пример.
Пусть задана транспортная сеть на множестве из шести уз-
лов. При этом I
p
= {1, 4}; I
t
{6}; I
k
= {2, 3, 5}; a
1
=30; a
2
=-20; a
3
=-20;
a
4
=30; a
5
=-20; a
6
=0. Граф транспортной сети и стоимости перево-
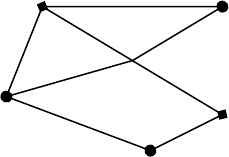
зок задаются в следующем виде:
1(30) 8 5(-20)
5 6 10
4 6(0) 4
2(-20) 4(30)
8 10
3(-20)
0). Исходное состояние: k = 1;
А
1
= (30, 20, 20, 30, 20, 0);
текущий путь (i,j)=(1,2).
Итерация 1. k = 1;
x
12
= 20; А
2
= (10, 0, 20, 30, 20, 0);
(i,j)=(1, 5).
Итерация 2. k = 2;
x
15
= 10; А
3
= (0, 0, 20, 30, 10, 0);
(i,j)=(4, 3).
Итерация 3. k = 3;
x
43
= 20; А
4
= (0, 0, 0, 10, 10, 0);
(i,j)=((4,6), (6,5)).
Итерация 4. k = 4;
x
46
= x
65
= 10; А
5
= (0, 0, 0, 0, 0, 0);
∀А
5
i
= 0; - конец.
Исходный опорный план построен:

118
x
12
= 20; x
15
= 10; x
43
= 20; x
46
= x
65
= 10;
значение целевой функции (стоимость перевозок)
L = 5×20 + 8×10 + 10×20 + 4×10 + 10×10 = 520.
Метод потенциалов.
В (6.1) был рассмотрен метод потенциалов, предназначен-
ный для решения транспортных задач. Рассмотрим особенности
применения этого метода для решения транспортной задачи в
сетевой постановке [78]. Математическая модель задачи описы-
вается выражениями (6.15)-(6.17). Решение двойственной задачи
будет иметь вид
μ = (V
1
,...,V
j
,...,V
n
)
т
,
где V
j
называют потенциалом j -го узла сети, и он характеризует
эффективность изменения a
j
. Тогда разность потенциалов │V
j
-V
i
│
характеризует эффективность перевозки.
Все перевозки J, определяемые опорным решением x= ║x
s
x
q
║, можно разбить на два подмножества J = S ∪ Q,
где S - базисные перевозки S = { (i,j)∈J │ x
ij
> 0 } .
Q - небазисные перевозки Q = { (i,j)∈J │ x
ij
= 0 } .
Если (i,j) ∈ S, то (V
j
- V
i
) = c
ij
.
Если ∀(i,j) ∈ Q, │V
j
- V
i
│< c
ij
, то нет перевозок, которые целе-
сообразно запланировать, следовательно, решение оптимально.
Если ∃(α,β) ∈ Q, │V
β
- U
α
│ > c
αβ
, тогда, если (V
β
- U
α
)>0, то пе-
ревозку K = (α,β) целесообразно ввести в число базисных, если
(V
β
- U
α
)<0, то в базис следует ввести перевозку K = (β,α).
Рассмотрим алгоритм решения транспортной задачи в се-
тевой постановке.
a). Анализ оптимальности текущего решения. Определе-
ние перевозки, вводимой в базис.
♦ Вычисляются потенциалы V
j
из системы уравнений
V
j
- V
i
- c
ij
= 0, ∀(i,j) ∈ S,
причем V
1
= const, например, V
1
= 0.
♦ Рассчитывается невязка
η(α,β) = max (│V
j
- V
i
│ - c
ij
).
(i,j)∈Q
Если η(α,β)≤0, то решение оптимально. Процесс заканчивается.
Если η(α,β)>0, то определяется перевозка, вводимая в базис:
если (V
β
- V
α
) > 0, то перевозка K = (α,β) вводится в базис S;
если (V
β
- V
α
) < 0, то перевозка K = (β,α) вводится в базис S.
119
б). Нахождение перевозки, выводимой из базиса.
♦ Строится ε-маршрут.
♦ Рассчитывается ε :
ε = min x
-
ij
, (i,j) ∈ S
Перевозка R = (γ,δ), на которой достигается ε, выводится из ба-
зиса S.
в). Строится новый граф перевозок
♦ Новый базис S′ вычисляется как
S′ = S ∪ K \ R.
♦ В новом опорном решении x′ изменяется значение перевозок
на ε-маршруте по правилу
x
ij
′
-
= x
ij
-
- ε
x
ij
′
+
= x
ij
+
+ ε
♦ Вычисляется новое значение целевой функции
L(x′) = L(x) - ηε.
Пример.
Применим рассмотренный алгоритм для улучшения опор-
ного решения, полученного методом минимального элемента в
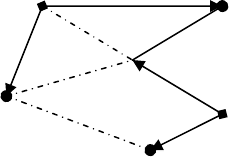
предыдущем примере. Опорное решение имеет вид:
1(30) 8(10) 5(-20)
5 (20) 6 10(10)
4 6(0) 4(10)
2(-20) 4(30)
8 10 (20)
3(-20)
Значение целевой функции L = 520.
Итерация 1.
а).
♦ Вычисляются потенциалы
V
j
- U
i
- c
ij
= 0, ∀(i,j) ∈ S, V
1
= 0.
Тогда V
1
= 0; V
2
= 5; V
3
= 4; V
4
= -6; V
5
= 8; V
6
= -2.
♦ Рассчитываются невязки
η(i,j) = (│V
j
- V
i
│ - c
ij
) для (i,j)∈Q
η(1,6) = 2 - 6 = -4;
120
η(2,6) = 7 - 4 = +3;
η(2,3) = 1 - 8 = -7;
η(2,6) = max η(i,j) = 3, т.к. (V
6
- V
2
) = -7 < 0, то K = (6,2).
б).
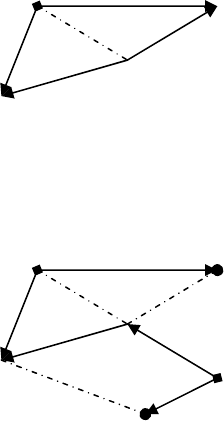
♦ Строится ε-маршрут
1(30) 8(10) 5(-20)
5 (20) 10(10)
6(0)
ε
2(-20)
(6,2) - (1,2) - (1,5) - (6,5)
+ - + -
♦ Рассчитывается ε = min {20, 10} = 10.
в). Строится новый граф перевозок
1(30) 8(20) 5(-20)
5 (10) 6 10
4(10) 6(0) 4(10)
2(-20) 4(30)
8 10 (20)
3(-20)
Значение целевой функции L = 520 – 3×10 = 490.
Итерация 2.
а).
♦ Вычисляются потенциалы
V
j
- U
i
- c
ij
= 0, ∀(i,j) ∈ S, V
1
= 0.
Тогда V
1
= 0; V
2
= 5; V
3
= 7; V
4
= -3; V
5
= 8; V
6
= 1.
♦ Рассчитываются невязки
η(i,j) = (│V
j
- V
i
│ - c
ij
) для (i,j)∈Q
η(1,6) = 1 - 6 = -5;
η(2,3) = 2 - 8 = -6;
η(5,6) = 7 - 10 = -3;
η(5,6) = max η(i,j) = -3 < 0, следовательно, решение, полученное
на предыдущей итерации оптимально.
