Москвин Б.В. Теория принятия решений
Подождите немного. Документ загружается.

141
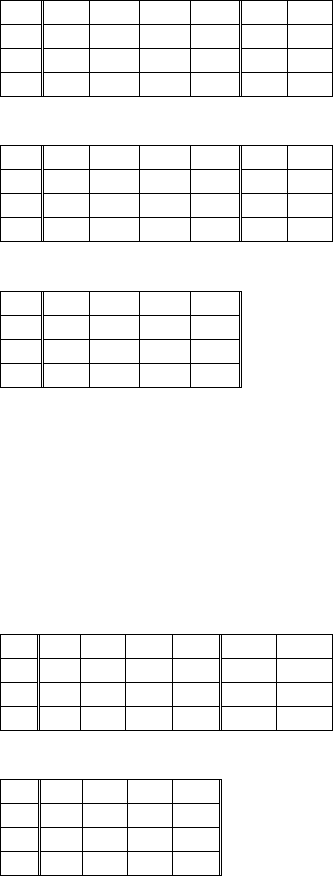
Итерация 2: δ
k
= -3; k = 3; θ
r
= 0; r = 2.
2
-
18.0 3.0 -1.0 -1.0 -4.0 -4.0
1 2.0 1.0 0.0 0.0 -1.0 -1.0
6 0.0 -2.0 1.0 0.0 2.0 0.0
7 18.0 -1.0 0.0 1.0 1.0 0.0
Итерация 3: δ
k
= -4.5; k = 2; θ
r
= 4; r = 3.
3
-
18.0 0.0 0.5 -1.0 -4.5 -4.5
1 2.0 1.0 0.5 0.0 -0.5 1.0
3 0.0 -1.0 0.5 0.0 -1.5 -1.0
7 18.0 0.0 -0.5 1.0 4.5 4.0
Итерация 4: δ
k
= 0; - решение оптимально.
4 0.0 0.0 0.0 0.0
1 4.0 0.0 0.44 0.11
3 6.0 -1.0 0.33 0.33
2 4.0 0.0 -0.11 0.22
Значение целевой функции равно 0, следовательно, опти-
мальное решение вспомогательной задачи является опорным
решением основной задачи, и оно может быть взято в качестве
исходного опорного решения x
s
.
Далее, для перехода к решению основной задачи необхо-
димо произвести замену 0-ой строки таблицы по правилу
L(x
s
) = c
т
s
x
s
; π
т
=c
т
s
S
-1
.
Тогда симплекс таблица будет иметь вид:
Итерация 5: δ
k
= -0.56; k = 4; θ
r
= 9; r = 1.
5 0.0 0.0 -0.56 0.11
-
0.56 -0.56
1 4.0 1.0 0.44 0.11 0.44 1.0
3 6.0 -1.0 0.33 0.33 0.33 -1.0
2 4.0 0.0 -0.11 0.22 -0.11 4.0
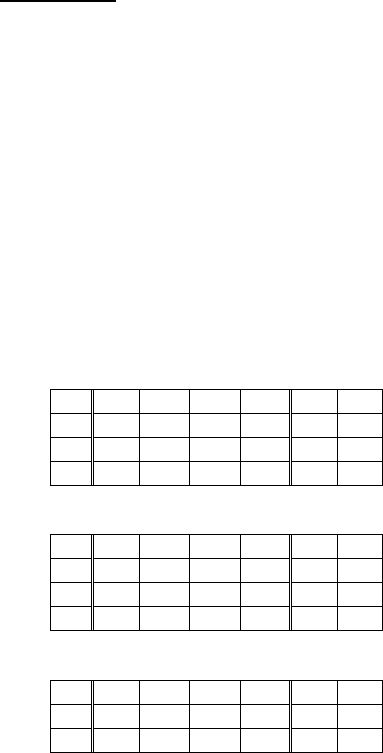
Итерация 6: δ
k
= 0; - решение оптимально.
6 5.0 0.0 0.0 0.25
4 9.0 0.0 1.0 0.25
3 3.0 -1.0 0.0 0.25
2 5.0 0.0 0.0 0.25
142
В ходе решения вспомогательной задачи выявляется факт
отсутствия в основной задаче допустимых решений. Действи-
тельно, если в оптимальном решении вспомогательной задачи
присутствуют дополнительные переменные, то, следовательно,
не существует ни одного набора переменных основной задачи,
позволяющего сформировать базис. Рассмотрим задачу, приве-
денную в примере 7.3:
Пример 7.8.
1x
1
+ 2x
2
→ max
1x
1
- 1x
2
≤ 2
1x
1
+ 1x
2
≤ 4
2x
1
+ 1x
2
≥ 14
x
1
,x
2
≥ 0
Приведем задачу к канонической форме
1x
1
+ 2x
2
→ max
1x
1
- 1x
2
+ x
3
= 2
1x
1
+ 1x
2
+ x
4
= 4
2x
1
+ 1x
2
- x
5
= 14
x
1
,...,x
5
≥ 0.
Решим вспомогательную задачу с использованием сим-
плекс-метода:
Итерация 1: δ
k
= -4; k = 1; θ
r
= 2; r = 1.
1
-
20.0 -1.0 -1.0 -1.0 -4.0 -4.0
6 2.0 1.0 0.0 0.0 1.0 1.0
7 4.0 0.0 1.0 0.0 1.0 1.0
8 14.0 0.0 0.0 1.0 2.0 2.0
Итерация 2: δ
k
= -5; k = 2; θ
r
= 1; r = 2.
2
-
12.0 3.0 -1.0 -1.0 -5.0 -5.0
1 2.0 1.0 0.0 0.0 -1.0 -1.0
7 2.0 -1.0 1.0 0.0 2.0 1.0
8 10.0 -2.0 0.0 1.0 3.0 1.0
Итерация 3: δ
k
= 0; - решение оптимально.
3 -7.0 0.5 1.5 -1.0
1 3.0 0.5 0.5 0.0
2 1.0 -0.5 0.5 0.0
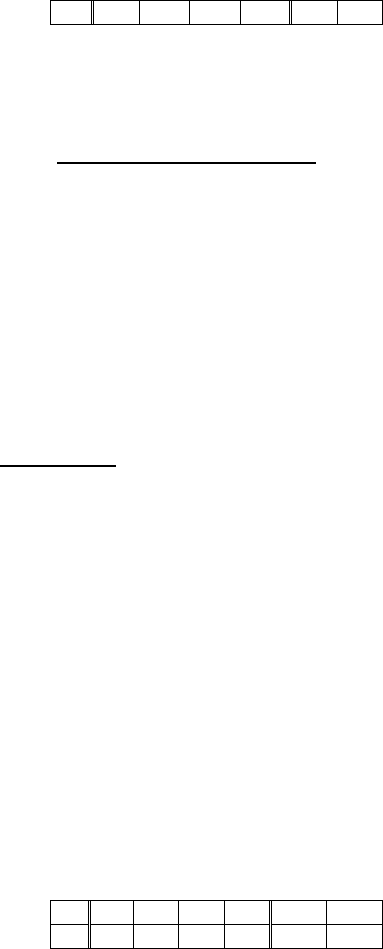
143
8 7.0 -0.5 -1.5 1.0
Вспомогательная задача решена. Значение целевой функ-
ции меньше 0, следовательно, множество решений исходной за-
дачи пусто. И это, действительно, так - см. пример 7.3.
М-метод решения задачи
М-метод представляет собой способ одновременного ре-
шения задачи построения исходного опорного решения и основ-
ной задачи линейного программирования. В этом случае задача
имеет вид
c
т
x - M
т
x
d
→ max,
A x + E x
d
= b,
x ≥ 0, x
d
.≥ 0,
здесь вектор x
d
является исходным опорным решением, а М -
достаточно большие числа.
Решим задачу из примера 7.4 с использованием М-метода.
Пример 7.9.
-1x
1
+ 1x
2
+ 1x
3
- 1x
4
→ max
1x
1
+ 1x
2
- 1x
3
- 1x
4
- 1x
5
= 2
2x
1
- 1x
2
- 2x
3
+ 1x
4
+ 1x
6
= 4
1x
1
+ 4x
2
- 1x
3
- 4x
4
+ 1x
7
= 20
x
1
,...,x
7
≥ 0.
Пусть М = 10, тогда задачу можно переписать
-1x
1
+ 1x
2
+ 1x
3
- 1x
4
-10x
8
-10x
9
-10x
10
→ max
1x
1
+ 1x
2
- 1x
3
- 1x
4
- 1x
5
+ 1x
8
= 2
2x
1
- 1x
2
- 2x
3
+ 1x
4
+ 1x
6
+ 1x
9
= 4
1x
1
+ 4x
2
- 1x
3
- 4x
4
+ 1x
7
+ 1x
10
= 20
x
1
,...,x
10
≥ 0.
Используем для решения последней задачи симплекс-
метод. Исходное опорное решение очевидно.
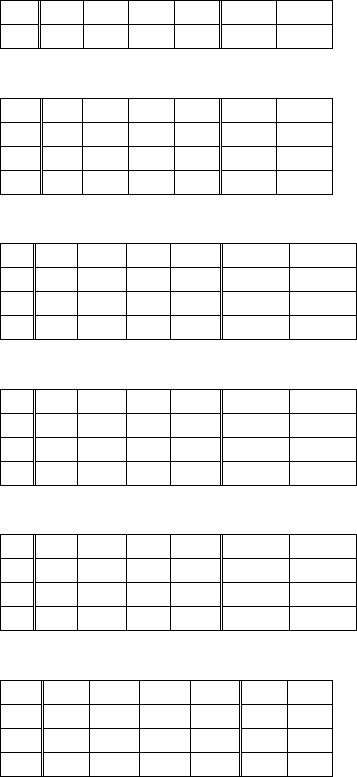
Итерация 1: δ
k
= -41; k = 2; θ
r
= 2; r = 1.
1
-
260 -10.0-10.0-10.
0
-
41.0 -41.0
8 2.0 1.0 0.0 0.0 1.0 1.0
144
9 4.0 0.0 1.0 0.0 -1.0 -1.0
1
0
2
0.0 0.0 0.0 1.0 4.0 4.0
Итерация 2: δ
k
= -31; k = 5; θ
r
= 3; r = 3.
2
-
178 31.0-10.0-10.
0
-
31.0 -31.0
2 2.0 1.0 0.0 0.0 -1.0 -1.0
9 6.0 1.0 1.0 0.0 -1.0 0.0
10 12.0 -4.0 0.0 1.0 4.0 0.0
Итерация 3: δ
k
= -21.25; k = 1; θ
r
= 4; r = 2.
3 -85 0.0 -10.
0
-2.25
-
21.25 -21.25
2 5.0 0.0 0.0 0.25 0.25 1.0
9 9.0 0.0 1.0 0.25 2.25 2.0
5 3.0 -1.0 0.0 0.25 -0.75 1.0
Итерация 4: δ
k
= -0.55; k = 6; θ
r
= 9; r = 2.
4 0.0 0.0 -0.5
5
0.11 -0.55 -0.55
2 4.0 0.0 -0.11 0.22 -0.11 0.0
1 4.0 0.0 0.44 0.11 0.44 1.0
5 6.0 -1.0 0.33 0.33 0.33 0.0
Итерация 5: δ
k
= -1.25; k = 3; θ
r
= 4; r = 3.
5 5.0 0.0 0.0 0.25 -1.25 -1.25
2 5.0 0.0 0.0 0.25 -0.25 -1.0
6 9.0 0.0 1.0 0.25 -2.25 -2.0
5 3.0 -1.0 0.0 0.25 0.75 -1.0
Итерация 6: δ
k
= 0; - решение оптимально.
6 10.0 -1.66 0.00 0.66
2 6.0 -0.33 0.00 0.33
6 18.0 -3.00 1.00 1.00
3 4.0 -1.33 0.00 0.33
В результате решения данной задачи получим, что опти-
мальное значение целевой функции равно 10, а оптимальное
решение имеет вид x
*
= (0 6 4 0 0 18)
т
.
7.2.4. Вырожденные задачи. Зацикливание
(см. п.3.7)

145
В вырожденных задачах линейного программирования на-
рушается взаимно однозначное соответствие между опорными
решениями и базисами. Одному и тому же вырожденному опор-
ному решению может соответствовать несколько базисов (соот-
ветственно, и вершин многогранника решений). Такая ситуация
может привести к зацикливанию симплекс-метода - периодиче-
скому возвращению через несколько итераций к одному и тому
же базису.
Пример 7.10.
Рассмотрим задачу
0.3x
1
- 5x
2
+ 0.1x
3
- 6x
4
→ max
0.1x
1
- 2x
2
- 0.2x
3
+ 9x
4
≤ 0
0.2x
1
- 3x
2
- 0.1x
3
+ 3x
4
≤ 0
5.0x
3
≤ 1
x
1
,x
2
,x
3
,x
4 .
≥ 0.
Задача поставлена в стандартной форме, следовательно,
она имеет очевидное исходное опорное решение. Используем
симплекс-метод:
Итерация 1; J
s
= { 5 6 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 2; J
s
= { 1 6 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 3; J
s
= { 1 2 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 4; J
s
= { 3 2 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 5; J
s
= { 3 4 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 6; J
s
= { 5 4 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 7; J
s
= { 5 6 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 8; J
s
= { 1 6 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 9; J
s
= { 1 2 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 10; J
s
= { 3 2 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 11; J
s
= { 3 4 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 12; J
s
= { 5 4 7 }; x
s
= ( 0.0 0.0 1.0 )
т
и так далее,..... Одному и тому же вырожденному опорному ре-
шению соответствуют различные базисы. На 7-ой итерации алго-
ритм возвратился к исходному опорному базису, и на последую-
щих итерациях базисы повторяются. Произошло зацикливание
алгоритма.
Использование рассмотренного в п.3.7 способа преодоле-
ния зацикливания позволяет получить оптимальное решение
Итерация 1; J
s
= { 5 6 7 }; x
s
= ( 0.0 0.0 1.0 )
т

146
Итерация 2; J
s
= { 1 6 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 3; J
s
= { 1 2 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 4; J
s
= { 3 2 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 5; J
s
= { 3 4 7 }; x
s
= ( 0.0 0.0 1.0 )
т
Итерация 6; J
s
= { 3 4 1 }; x
s
= ( 0.200 0.004 0.040 )
т
Итерация 7; J
s
= { 3 5 1 }; x
s
= ( 0.200 0.030 0.100 )
т
Итак, оптимальное решение x
*
= ( 0.1 0 0.2 0 0.03 0 0)
т
; L
*
=
0.05.
7.3. Нелинейное программирование
Будем рассматривать задачу нелинейного программирова-
ния в следующем виде
f(x) → max,
ϕ
I
(x) ≤ b
i
, i= 1,..., m,
x = (x
1
,x
2
,...,x
n
)
т
≥ 0,
где f(x) и все ϕ
i
(x), i = 1,..., m - выпуклые функции.
7.3.1. Градиентные методы
(см.п.4.3.1)
Градиентный метод представляет собой метод поиска экс-
тремума функции при отсутствии ограничений. Рассмотрим сле-
дующую задачу: найти максимум функции
f(x) = 16x
1
- 2x
2
1
+ 12x
2
- x
2
2
→ max.
Градиентный
метод
с
постоянным
шагом.
Отдельная итерация алгоритма градиентного метода с по-
стоянным шагом состоит в выполнении ряда шагов.
0). Исходное состояние. Задается начальная точка x
o
, шаг h, ко-
эффициент α, некоторое малое ε; k = 0.
1). Вычисляется ∇F(x
k
).
2). Находится x
k+1
= x
k
+ h ∇F(x
k
).
3). Рассчитывается f(x
k+1
); если f(x
k+1
) ≤ f(x
k
), то производится
дробление шага h = α h и производится переход на шаг 2.
4). Проверяется условие окончания процесса:
если ║x
k+1
-x
k
║≤ε или ║∇F(x
k
)║≤ε, то решение оптимально;
если ║x
k+1
-x
k
║>ε или ║∇F(x
k
)║>ε, то k=k+1; переход на шаг 1.
Пример 7.11.
147
0). Исходное состояние. Пусть начальная точка x
o
= (0,0); h = 1;
α = 0.6; ε = 0.1; k=0.
Итерация 1. x
o
= (0,0); h = 1; k = 0;
1). ∇F(x
o
) = (16 - 4x
1
, 12 - 2x
2
) = (16, 12);
2). x
1
= x
o
+ h ∇F(x
o
) = (16, 12);
3). f(x
1
) = -256 < f(x
o
) = 0 - следовательно, необходимо произ-
вести дробление шага h = 0.6 h = 0.6.
2). x
1
= x
o
+ h ∇F(x
o
) = (9.6, 7.2)
3). f(x
1
) = 3.84 > f(x
o
) = 0
4). ║ x
1
- x
о
║ > ε, следовательно, k = k+1.
Итерация 2. x
1
= (9.6, 7.2); h = 0.6; k = 1;
1). ∇F(x
1
) = (-22.4, -2.4)
2). x
2
= x
1
+ h ∇F(x
1
) = (-3.84, 5.76)
3). f(x
2
) = -55 < f(x
1
) = 3.84 - следовательно, необходимо произ-
вести дробление шага h = 0.6 h = 0.36.
2). x
2
= (9.6, 7.2) + 0.36 (-22.4, -2.4) = (1.54, 6.34);
3). f(x
2
) = 55.78 > f(x
1
) = 3.84;
4). ║ x
2
- x
1
║ > e, тогда k = k+1.
Итерация 3. x
2
= (1.54, 6.34); h = 0.36; k = 2;
1). ∇F(x
2
) = (9.84,-0.68);
2). x
3
= (1.54, 6.34) + 0.36 (9.84,-0.68) = (5.08, 6.10);
3). f(x
3
) = 65.66 > f(x
2
) = 55.78
4). ║ x
3
- x
2
║ > ε, тогда k = k+1.
Итерация 4. x
3
= (5.08, 6.10); h = 0.36; k = 3;
1). ∇F(x
3
) = (-4.32,-0.2);
2). x
4
= (5.08, 6.10) + 0.36 (-4.32,-0.20) = (3.52, 6.03);
3). f(x
4
) = 67.54 > f(x
3
) = 65.66
4). ║ x
4
- x
3
║ > ε, тогда k = k+1.
Итерация 5. x
4
= (3.52, 6.03); h = 0.36; k = 4;
1). ∇F(x
4
) = (1.92,-0.06);
2). x
5
= (3.52, 6.03) + 0.36 (1.92,-0.06) = (4.21, 6.01);
3). f(x
5
) = 67.91 > f(x
4
) = 67.54
4). ║ x
5
- x
4
║ > ε, тогда k = k+1.
Итерация 6. x
5
= (4.21, 6.01); h = 0.36; k = 5;
1). ∇F(x
5
) = (-0.84,-0.02);
2). x
6
= (4.21, 6.01) + 0.36 (-0.84,-0.02) = (3.91, 6.00);
3). f(x
6
) = 67.98 > f(x
5
) = 67.91
4). ║ x
6
- x
5
║ > ε, тогда k = k+1.
Итерация 7. x
6
= (3.91, 6.00); h = 0.36; k = 6;

148
1). ∇F(x
6
) = (0.36, 0.0);
2). x
7
= (3.91, 6.00) + 0.36 (0.36, 0.0) = (4.04, 6.00);
3). f(x
7
) = 68.00 > f(x
6
) = 67.98
4). ║ x
7
- x
6
║ > ε, тогда k = k+1. f(x) = 16x
1
- 2x
2
1
+ 12x
2
- x
2
2
.
Итерация 8. x
7
= (4.04, 6.00); h = 0.36; k = 7;
1). ∇F(x
7
) = (-0.16, 0);
2). x
8
= (4.04, 6.00) + 0.36 (-0.16, 0) = (3.98, 6.00);
3). f(x
8
) = 68.00 = f(x
7
) = 68.00
4). ║ x
8
- x
7
║ < ε, следовательно, оптимальное решение полу-
чено.
Итак, оптимальное решение x
*
= (3.98, 6.0)
т
; f(x
*
) = 68.
Градиентный метод наискорейшего подъема.
Решим ту же задачу методом наискорейшего подъема.
f(x) = 16x
1
- 2x
2
1
+ 12x
2
- x
2
2
→ max
Отдельная итерация алгоритма наискорейшего подъема
состоит в выполнении следующих шагов.
0). Задается начальная точка x
o
, некоторое малое ε; k = 0.
1). Вычисляется ∇F(x
k
).
2). Рассчитывается h
k
= мах f(x
k
+ h ∇f(x
k
)), h ≥ 0.
3). Находится x
k+1
= x
k
+ h
k
∇F(x
k
).
4). Проверяется условие окончания процесса:
если ║x
k+1
-x
k
║ ≤ ε или ║∇F(x
k
) ║ ≤ ε - решение оптимально.
если ║x
k+1
-x
k
║ > ε или ║∇F(x
k
) ║ > ε, то k = k+1.
Пример 7.12.
0). Исходное состояние. Начальная точка x
o
= (0,0); ε=0.1; k=0.
Итерация 1. k = 0; x
o
= (0,0);
1). ∇F(x
o
) = (16 - 4x
1
, 12 - 2x
2
) = (16, 12);
2). h
0
= max f (x
o
+ h ∇f (x
0
)) = max f (16h, 12h)=
= max (256h -512h
2
+ 144h - 144h
2
) = 0.3
3). x
1
=x
o
+h∇F(x
o
) = (4.8, 3.6); f(x
1
) = 60.96;
4). ║x
1
-x
o
║ > ε, k=k+1.
Итерация 2. k = 1; x
1
= (4.8, 3.6);
1). ∇F(x
1
) = (16 -4x
1
,12-2x
2
)
= (-3.2, 4.8)
2). h
1
= max f(4.8 -3.2h, 3.6 +4.8h) = 0.38
3). x
2
= x
1
+ h ∇F(x
1
) = (3.6, 5.4); f(x
2
) = 67.32;
4). ║x
2
- x
1
║ > ε, k = k+1.
Итерация 3. k = 2; x
2
= (3.6, 5.4);

149
1). ∇F(x
2
) = (16 - 4x
1
, 12 - 2x
2
) = (
1.6, 1.2)
2). h
2
= мах f(3.6 + 1.6h, 5.4 + 1.2h) = 0.3;
3). x
3
= x
2
+ h ∇F(x
2
) = (
4.1, 5.8); f(x
3
) = 67.95;
4). ║x
3
- x
2
║ > ε, k = k+1.
Итерация 4. k = 3; x
3
= (4.1, 5.8);
1). ∇F(x
2
) = (16 - 4x
1
, 12 - 2x
2
) = (-0.4, 0.4)
2). h
3
= мах f(4.1 - 0.4h, 5.8 + 0.4h) = 0.31;
3). x
4
= x
3
+ h ∇F(x
3
) = (
3.98, 5.92); f(x
4
) = 67.99;
4). ║x
4
- x
3
║ > ε, k = k+1.
Итерация 5. k = 4; x
4
= (3.98, 5.92);
1). ∇F(x
4
) = (16 - 4x
1
, 12 - 2x
2
) = ( 0.04, 0.16)
2). h
4
= мах f(3.98 + 0.04h, 5.92 + 0.16h) = 0.29 ;
3). x
5
= x
4
+ h VF(x
4
) = (
3.99, 5.97); f(x
4
) = 68.0;
4). ║x
5
- x
4
║ < ε - оптимальное решение получено.
Итак, оптимальное решение x
*
= (3.99, 5.97)
т
; f(x
*
) = 68.0.
7.3.2. Метод покоординатной оптимизации
(см.п.4.3.1)
Рассмотрим особенности применения алгоритма покоорди-
натной оптимизации на примере рассмотренной ранее задачи
(см. примеры 7.11, 7.12)
f(x) = 16x
1
- 2x
2
1
+ 12x
2
- x
2
2
→ max
Алгоритм заключается в последовательном выполнении
итераций, каждая из которых состоит в выполнении ряда шагов.
Задается начальная точка x
o
; величина шага h; параметр дробле-
ния шага α∈(0,1), критерии окончания итерационного процесса
некоторое малое ε > 0 и δ > 0; номер цикла c = 0, номер итерации
k = 0. Т.к. x=(x
1
, x
2
), то n = 2.
Пример 7.13.
0). Исходное состояние. x
o
= (0,0); h = 2; α = 0.5; ε = 0.1; δ = 0.1;
c = 0; k = 0; n = 2.
Итерация 1. x
o
= (0,0); h = 1; c = 0; k = 0;
1). Вычисляется номер проверяемой координаты вектора x на
итерации k; i(k) = k - c n + 1; i(0) = 1;
2). Вычисляется значение функции
f(x
k
+ h e
i
(k)) = f(0 + 2, 0) = 24; т.к. e
1
(0) = (1,0)
т.к. f(x
k
+ h e
i
(k)) = 24 > f(x
k
) = 0, то x
k+1
= x
k
+ h e
i
(k) = (2, 0),
3). k = k + 1 = 1; вычисляется c' = [k/n] = 0; т.к. c' = c, т.е. номер
цикла не изменился, то производится переход на шаг 1.
Итерация 2. x
1
= (2,0); h = 2; c = 0; k = 1;
150
1). i(1) = k - c n + 1; i(1) = 2; e
2
(1) = (0.1)
2). f(x
k
+he
i
(k)) = f(2,2) = 44 > f(x
k
) = 24, то x
k+1
= x
k
+he
i
(k) = (2,2),
3). k = k + 1 = 2; вычисляется c' = 1; т.к. c' > c, то c = c' = 1. Оце-
нивается удачность цикла 0; цикл удачный, т.к. была удач-
ная итерация; производится переход на шаг 4;
4). Т.к. ║x
2
- x
1
║ > ε, то производится переход на шаг 1.
Итерация 3. x
2
= (2, 2); h = 2; c = 1; k = 2;
1). i(2) = k - c n + 1 = 1;
2). f(x
k
+ h e
i
(k)) = f(4, 2) = 52 > f(x
k
) = 44, то x
3
= (4, 2),
3). k = k + 1 = 3; вычисляется c' = 1;
т.к. c' = c = 1, производится переход на шаг 1;
Итерация 4. x
3
= (4,2); h = 2; c = 1; k = 3;
1). i(3) = k - c n + 1 = 2;
2). f(x
k
+ h e
i
(k)) = f(4, 4) = 64 > f(x
k
) = 52, то x
4
= (4, 4),
3). k = k + 1 = 4; вычисляется c' = 2 > c, то c = c' = 2.
Цикл удачный, т.к. была удачная итерация.
4). Т.к. ║x
4
- x
3
║ > ε, то производится переход на шаг 1.
Итерация 5. x
4
= (4, 4); h = 2; c = 2; k = 4;
1). i(4) = k - c n + 1 = 1;
2). f(x
k
+ h e
i
(k)) = f(6, 4) = 56 < f(x
k
) = 64, то
f(x
k
- h e
i
(k)) = f(2, 4) = 56 < f(x
k
) = 64, то
x
5
= x
4
= (4, 4) - итерация неудачна.
3). k = k + 1 = 5; вычисляется c'= 2;
т.к. c' = c = 2, производится переход на шаг 1;
Итерация 6. x
5
= (4,4); h = 2; c = 2; k = 5;
1). i(5) = k - c n + 1 = 2;
2). f(x
k
+ h e
i
(k)) = f(4, 6) = 68 > f(x
k
) = 64, то x
6
= (4, 6),
3). k = k + 1 = 6; вычисляется c' = 3 > c, то c = c' = 3.
Цикл удачный, т.к. была удачная итерация.
4). Т.к. ║x
6
- x
5
║ > ε, то производится переход на шаг 1.
Итерация 7. x
6
= (4, 6); h = 2; c = 3; k = 6;
1). i(6) = k - c n + 1 = 1;
2). f(x
k
+ h e
i
(k)) = f(6, 6) = 60 < f(x
k
) = 68, то
f(x
k
- h e
i
(k)) = f(2, 6) = 60 < f(x
k
) = 68, то
x
7
= x
6
= (4, 6) - итерация неудачна.
3). k = k + 1 = 7; вычисляется c' = 3; т.к. c' = c = 3, производится
переход на шаг 1;
Итерация 8. x
7
= (4,6); h = 2; c = 3; k = 7;
1). i(7) = k - c n + 1 = 2;
2). f(x
k
+ h e
i
(k)) = f(4, 8) = 64 < f(x
k
) = 68, то
f(x
k
- h e
i
(k)) = f(4, 4) = 64 < f(x
k
) = 68, то
