Москвин Б.В. Теория принятия решений
Подождите немного. Документ загружается.


131
5x
14
+
5x
24
+
5x
34
= 20
5x
11
+ 5x
12
+ 5x
13
+ 5x
14
+ x
д1
= 62
5x
21
+ 5x
22
+ 5x
23
+ 5x
24
+ x
д2
= 45
5x
31
+ 5x
32
+ 5x
33
+ 5x
34
+ x
д3
= 37
x
ij .
≥ 0, i=1,2,3, j = 1,2,3,4.
Решение, которое ищется в данной задаче, однозначно
описывается вектором x, имеющим 15 неотрицательных компо-
нент x = ║x
11
x
12
x
13
x
14
x
21
x
22
x
23
x
24
x
31
x
32
x
33
x
34
x
д1
x
д2
x
д3
║
т
. Тогда
задача может быть представлена в векторно матричной форме
L = f
т
x → min
A x = b,
x ≥ 0,
или
║19 12 18 21 10 16 13 14 29 14 16 15 0 0 0 ║ x → min
5000500050 0 0000 25
0500050005 0 0000 30
0050005000 5 0000 15
A = 0005000500 0 5000 x = 20
5555000000 0 0100 62
0000555500 0 0010 45
0000000055 5 5001 37
Решение данной задачи на основе симплекс-метода позво-
ляет получить следующие результаты:
- минимальное значение целевой функции, равное 220.0;
- решение прямой задачи
x
*
=║ 0 6 0 0 5 0 3 1 0 0 0 3 32 0 22║
т
;
- решение двойственной задачи
μ
*
= ║ 2.2 2.4 2.8 3.0 0 -0.2 0║
т
.
Анализ результатов решения.
В результате решения поставленной задачи получен план
перевозок материалов из населенных пунктов на строительные
площадки ОКИК, при этом минимальный суммарный расход бен-
зина составляет 220 литров.
132
Анализируя результаты решения прямой задачи линейного
программирования (x
*
= ║0 6 0 0 5 0 3 1 0 0 0 3 32 0 22║
т
), можно
заключить, что
- на первую строительную площадку целесообразно отправить
5 машин с базы, расположенной во 2 населенном пункте;
- на вторую строительную площадку целесообразно отправить
6 машин с базы, расположенной в 1 населенном пункте;
- на третью строительную площадку целесообразно отправить
3 машины с базы, расположенной во 2 населенном пункте;
- на четвертую строительную площадку целесообразно
отпра-
вить 1 машину с базы, расположенной во 2 населенном пункте, и
3 машины с базы, расположенной в 3 населенном пункте;
При этом со второй базы будут вывезены все материалы,
т.к. x
д2
= 0; на первой базе останется 32 и на третьей 22 тонны
материала.
Анализ результатов решения двойственной задачи показы-
вает, что (μ
*
= ║ 2.2 2.4 2.8 3.0 0 -0.2 0 ║
т
):
- оптимальное значение целевой функции прямой и двойст-
венной задачи равны c
т
x* = b
т
μ* = 220;
- если потребности строительных площадок в материалах бу-
дут увеличиваться, то расход бензина будет расти, причем более
всего он будет расти, если увеличиваются потребности СП
4
(т.к.
μ
4
= 3.0), и менее всего, если увеличиваются потребности СП
1
(т.к. μ
1
= 2.2);
- увеличение запасов материалов на базах пунктов НП
1
и НП
3
не влияет на расход бензина (μ
1
= 0, μ
3
= 0), в то же время увели-
чение количества материалов на базе НП
2
позволяет снизить
расход бензина, необходимого на перевозку (μ
2
= -0.2).
7.2. Линейное программирование
Рассмотрим задачу линейного программирования, постав-
ленную в следующем виде
L = c
т
x → max
A x ≤ b
x ≥ 0
Здесь А - матрица условий размерности m×n;
c
т
- вектор коэффициентов целевой функции размерности
1×n;
b - вектор ограничений размерности m×1;
133
x - решение.
7.2.1. Графо-аналитический способ решения задач
(см.п.3.3)
Графо-аналитический способ решения задач обладает дос-
таточной наглядностью, позволяет уяснить основные особенно-
сти задач линейного программирования, с его помощью можно
решать задачи линейного программирования, когда m=2 или n=2.
Рассмотрим особенности использования метода на приме-
ре следующей задачи
Пример 7.1.
2x
1
+ 14x
2
+ 22x
3
+ 4x
4
→ min
3x
1
+ 1x
2
- 4x
3
- 2x
4
≤ 1
1x
1
+ 3x
2
+ 1x
3
- 3x
4
.
≥ 1
x
j
≥ 0, j = 1,2,3,4.
Приведем задачу к стандартному виду
- 2x
1
- 14x
2
- 22x
3
- 4x
4
→ max
3x
1
+ 1x
2
- 4x
3
- 2x
4
≤ 1
- 1x
1
- 3x
2
- 1x
3
+ 3x
4
≤ -1
x
j
≥ 0, j = 1,2,3,4.
Для данной задачи запишем двойственную задачу
1μ
1
- 1μ
2
→ min
3μ
1
- 1μ
2
≥. - 2
1μ
1
- 3μ
2
≥ -14
-4μ
1
- 1μ
2
≥ -22 μ
2
-2μ
1
+ 3μ
2
≥ - 4
μ
1
,μ
2
≥ 0
Избавляемся от "-" в правой части.
-1μ
1
+ 1μ
2
→ max 4
-3μ
1
+ 1μ
2
≤ 2
-1μ
1
+ 3μ
2
≤ 14 2
4μ
1
+ 1μ
2
≤ 22
2μ
1
- 3μ
2
≤ 4, μ
1
,μ
2
≥ 0 . 0 2 4 6 μ
1
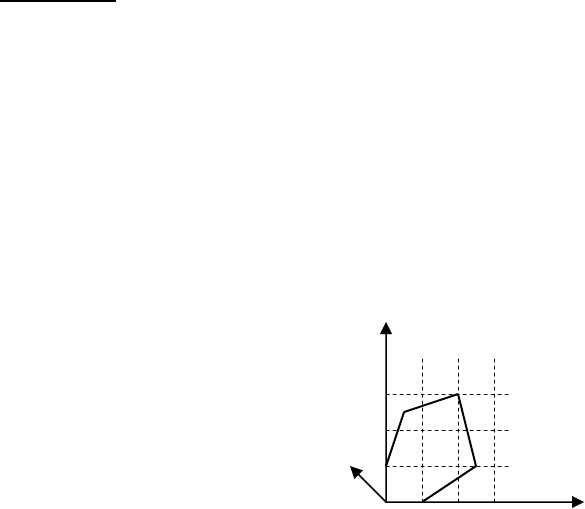
Суть графо-аналитического способа решения состоит в
том, что градиент, затем строится линия уровня L(μ) = -1μ
1
+ 1μ
2
= А (в общем случае это гиперплоскость), которая перпендику-
лярна градиенту. Все решения, находящиеся на этой линии,
имеют одинаковое значение целевой функции равное А. Далее
эта линия перемещается параллельно самой себе в направлении
возрастания градиента до тех пор, пока линия уровня не достиг-
134
нет границы допустимой области. Решения, которые соответст-
вуют пересечению линии уровня и границы допустимой области,
являются оптимальными.
Для рассматриваемой задачи оптимальное решение соот-
ветствует точке (1,5), L (1,5) = -4.
Проведем анализ полученного решения двойственной задачи.
♦ 3-е и 4-е уравнения выполняются как строгие неравенства,
следовательно, в соответствии с условиями дополняющей неже-
сткости (см. ф.(2.6) и
п.3.1) x
3
= x
4
= 0.
♦ 1-е и 2-е уравнения выполняются как равенства, следова-
тельно, в соответствии с условиями дополняющей нежесткости
(см. ф.(2.6) и п.3.1) x
1
> 0, x
2
> 0.
С учетом проведенного анализа, в результате которого бы-
ло установлено, что x
3
= x
4
= 0 исходную задачу можно перепи-
сать как L = -2x
1
-14x
2
3x
1
+ 1x
2
= 1
1x
1
+ 3x
2
= 1
Откуда x
1
= 0.25; x
2
= 0.25; L = -4.
Так как в процессе приведения исходной задачи к стан-
дартному виду была проведена замена целевой функции, то
окончательное решение имеет вид x
*
= (0.25 0.25 0 0); L
*
= 4.
Замечание 1.
Если решение исходной задачи вырожденное, то опти-
мальное решение двойственной задачи достигается в
несколь-
ких крайних точках
(множество оптимальных решений). Дейст-
вительно, пусть исходная задача имеет вид
Пример 7.2.
2x
1
+ 14x
2
+ 22x
3
+ 4x
4
→ min
3x
1
+ 1x
2
- 4x
3
- 2x
4 ,
≤ 1
1x
1
+ 3x
2
+ 1x
3
- 3x
4
.≥ 3 x
j
≥ 0, j = 1,2,3,4.
Тогда двойственная задача
- 1μ
1
+ 3μ
2
→ max μ
2
- 3μ
1
+ 1μ
2
≤ 2
- 1μ
1
+ 3μ
2
≤ 14 В С
4μ
1
+ 1μ
2
≤ 22 4
2μ
1
- 3μ
2
≤ 4
μ
1
, μ
2
≥ 0
0 2 4 6 μ
1
135
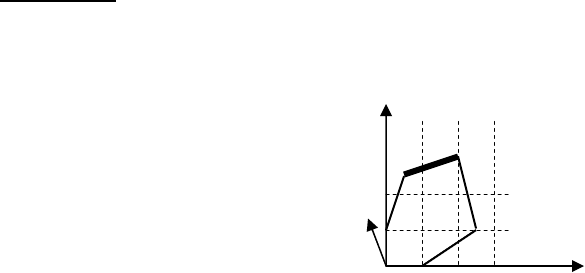
Оптимальное решение двойственной задачи достигается в
двух крайних точках В и С (следовательно, в задаче бесконечное
множество оптимальных решений – отрезок ВС). В этом случае
решение исходной задачи является вырожденным
x* = (0 1 0 0); L* = 14.
Замечание 2.
Если целевая функция исходной задачи может неограни-
ченно возрастать
(убывать), т.е. оптимального решения не
существует, то множество допустимых решений двойственной
задачи
пусто (Δ = ∅).
Пример 7.3.
Рассмотрим задачу
2x
1
+ 4x
2
- 14x
3
→ min
1x
1
+ 1x
2
- 2x
3
≥ 1
-1x
1
+ 1x
2
- 1x
3
≥ 2
x
j
≥ 0, j = 1,2,3,4.
Задача двойственная к данной:
μ
2
1μ
1
+ 2μ
2
→ max
1μ
1
- 1μ
2
≤ 2 4
1μ
1
+ 1μ
2
≤ 4 Δ = ∅
2μ
1
+ 1μ
2
≥ 14 2
μ
1
, μ
2
≥ 0
0 2 4 6 μ
1
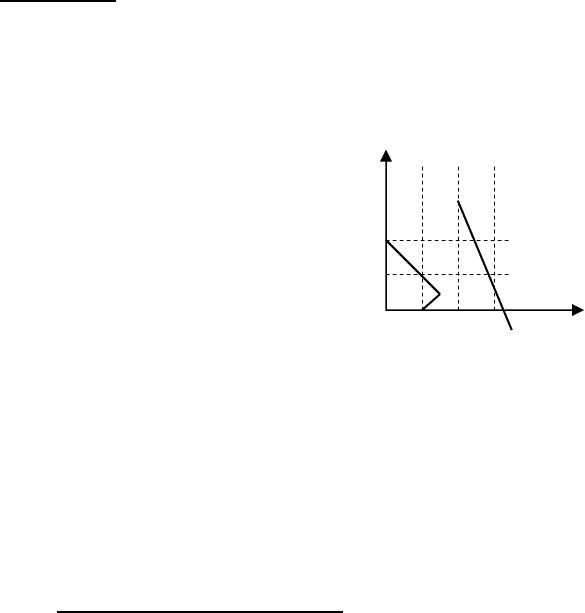
Множество допустимых решений двойственной задачи пус-
то. При решении прямой задачи, если x
1
= 0; а переменные x
2
,x
3
изменяются в пропорции 3x
2
= x
3
, то все такие решения при лю-
бых x
2
,x
3
являются допустимыми, в тоже время целевая функция
неограниченно убывает.
Замечания 1 и 2 справедливы, если на место прямой зада-
чи поставить двойственную задачу, а на место двойственной -
прямую.
7.2.2. Симплекс-метод решения задач
Каноническая форма задачи
Симплекс-метод является универсальным методом реше-
ния задач линейного программирования. Для его использования
задача должна быть сведена к канонической форме (ограничения
136
должны быть представлены в виде равенств). В канонической
форме может быть представлена любая задача линейного про-
граммирования.
Действительно, пусть имеется s-е ограничение вида
s
n
1j
jsj
b xa ≤
∑
=
, тогда в канонической форме
s1n
n
1j
jsj
b x xa =+
+
=
∑
Соответственно, если
k
n
1j
jkj
b xa ≥
∑
=
, тогда в канонической форме.
k1n
n
1j
jkj
b x xa =−
+
=
∑
Если переменные задачи могут принимать отрицательные
значения, т.е имеет место задача вида c
т
x → max
A x ≤ b ,
то ее следует преобразовать к виду:
c
т
y - c
т
z → max
Ay - A z ≤ b
y, z ≥ 0 .
Если в результате решения задачи y
j
> 0, то x
j
=y
j
> 0; если z
k
> 0,
то x
k-n
= -z
k
< 0.
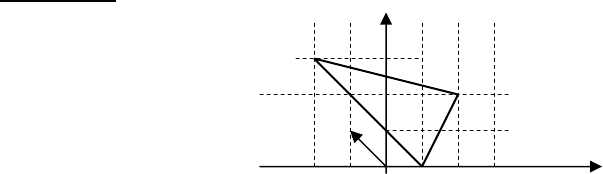
Пример 7.4.
Рассмотрим следующую задачу x
2
-1x
1
+ 1x
2
→ max
1x
1
+ 1x
2
≥ 2 4
2x
1
- 1x
2
≤ 4
1x
1
+ 4x
2
≤ 20
x
1
,x
2
∈ (-∞, +∞),
-4 -2 0 2 4 6 x
1
По условиям задачи переменные могут принимать о т р и -
ц а т е л ь н ы е значения. Задачу следует переписать в виде
-1y
1
+ 1y
2
+ 1z
1
– 1z
2
→ max
1y
1
+ 1y
2
- 1z
1
– 1z
2 .
≥ 2
2y
1
- 1y
2
- 2z
1
+ 1z
2 ,
≤ 4
1y
1
+ 4y
2
- 1z
1
– 4z
2
≤ 20,
y
1
,y
2
,z
1
,z
2 .
≥ 0.
Представим данную задачу в каноническом виде, для этого све-
дем ограничения вида неравенств к равенствам, тогда
-1x
1
+ 1x
2
+ 1x
3
- 1x
4
→ max
1x
1
+ 1x
2
- 1x
3
- 1x
4
- 1x
5
= 2
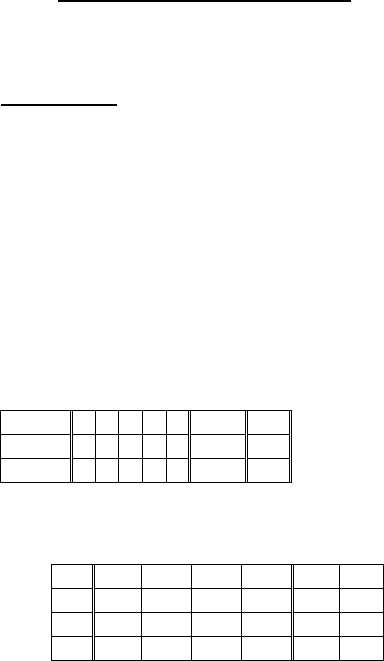
137
2x
1
- 1x
2
- 2x
3
+ 1x
4
+1x
6
= 4
1x
1
+ 4x
2
- 1x
3
- 4x
4
+1x
7
= 20,
x
1
,...,x
7
≥ 0.
В результате решения данной задачи (см. Пример.7.9) по-
лучим, что оптимальное значение целевой функции равно 10, а
оптимальное решение имеет вид x
*
= ( 0 6 4 0 0 18 0 )
т
, т.е.
x
1
=-4; x
2
=6.
Алгоритм симплекс-метода
(см. пп. 3.4, 3.5).
Рассмотрим особенности проведения итераций симплекс-
метода.
Пример 7.5.
2x
1
+ 1x
2
→ max
-1x
1
+ 1x
2
≤ 3
2x
1
- 1x
2
≤ 4
1x
1
+ 2x
2
≤ 12,
x
1
,x
2
≥ 0.
В канонической форме задача имеет вид
2x
1
+ 1x
2
→ max
-1x
1
+ 1x
2
+ 1x
3
= 3
2x
1
- 1x
2
+ 1x
4
= 4
1x
1
+ 2x
2
+ 1x
5
= 12, x
1
,x
2
,x
3
,x
4
,x
5 .
≥ 0.
В векторно-матричной форме
║ 2 1 0 0 0 ║ x → max
-1 1 1 0 0 3
2 -1 0 1 0 x = 4
1 2 5 0 1 12
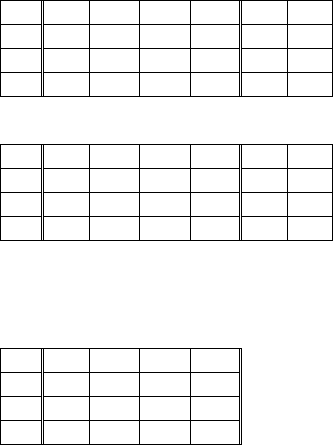
Поскольку задача поставлена в стандартной форме, то ис-
ходное опорное решение очевидно: x = (0 0 3 4 12)
т
. Исходная
симплекс-таблица имеет вид
0 0.0 0.0 0.0 0.0
3 3.0 1.0 0.0 0.0
4 4.0 0.0 1.0 0.0
5 12.0 0.0 0.0 1.0
Итерация 1:
1. Анализ оптимальности текущего решения; нахождение век-
тора, вводимого в базис.
138
Рассчитываются оценки (3.13)
δ
k
= min ( π
т
a
j
- c
j
)
,
j = 1,...,5.
δ
k
= min {-2 -1 0 0 0} = -2; k = 1.
Т.к. δ
k
< 0, k-ый вектор условий следует ввести в базис.
2. Установление неразрешимости задачи; нахождение векто-
ра, выводимого из базиса.
Вектор a
k
приводится к текущему базису - находится вектор æ
k
= S
-1
a
k
. Т.к. ∃ æ
ki
> 0, i=1,2,3, то задача разрешима и произво-
дится вычисление оценки θ
r
по формуле (3.15)
x
si
θ
r
= m i n ⎯
æ
ki
>0 æ
ki
θ
r
=
min { 2 12 } = 2; r = 2.
Приращение целевой функции (см.ф.3.12) ΔL = - δ
k
θ
r
= 4.
3. Преобразование базиса.
Исходная симплекс-таблица имеет вид
0 0.0 0.0 0.0 0.0 -2.0 -2.0
3 3.0 1.0 0.0 0.0 -1.0 -1.0
4 4.0 0.0 1.0 0.0 2.0 2.0
5 12.0 0.0 0.0 1.0 1.0 1.0
Преобразуем ее по рекуррентным формулам (3.17),(3.18)
1 4.0 0.0 1.0 0.0 -2.0 -2.0
3 5.0 1.0 0.5 0.0 0.5 1.0
1 2.0 0.0 0.5 0.0 -0.5 -1.0
5 10.0 0.0 -0.5 1.0 2.5 2.0
Итерация 2:
1. δ
k
= -2; k = 2.
2. θ
r
= 4; r = 3.
3.
2 12.0 0.0 0.6 0.8
3 3.0 1.0 0.6 -0.2
1 4.0 0.0 0.4 0.2
2 4.0 0.0 -0.2 0.4
Итерация 3:
1. δ
k
= 0, следовательно, текущее решение оптимально.
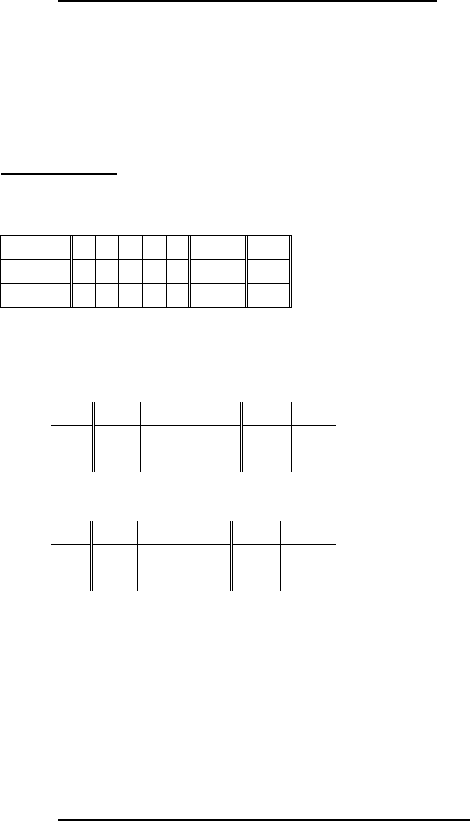
139
Таким образом, оптимальное решение поставленной зада-
чи линейного программирования x
*
= (4 4 3 0 0)
т
; L
*
= 12.
Решение двойственной задачи (0 0.6 0.8).
Неограниченность целевой функции
(см.п.3.4.3).
Ситуации, когда целевая функция неограниченно возраста-
ет на множестве допустимых решений, выявляются на втором
шаге алгоритма симплекс-метода, а именно при анализе вектора,
выводимого из базиса, так, если все компоненты æ
ki
≤ 0, то
имеет место такая ситуация.
Пример 7.6.
Рассмотрим задачу вида
║ 2 3 5 0 0 ║ x → max
-1 -2 1 1 0 2
x =
3 -1 -1 0 1 1
x ≥ 0.
Решим данную задачу с использованием симплекс-метода.
Итерация 1: δ
k
= -5; k = 3; θ
r
= 2; r = 1.
1 0.0 0.0 0.0 -5.0 -5.0
4 2.0 1.0 0.0 1.0 1.0
5 1.0 0.0 1.0 -1.0 -1.0
Итерация 2: δ
k
= -13; k = 2; θ
r
= ……
1 10.0 5.0 0.0
-
13.0 -13.0
3 2.0 1.0 0.0 -2.0 -2.0
5 3.0 1.0 1.0 -3.0 -1.0
Все компоненты æ
ki
<
0, следовательно, целевая функция
может неограниченно возрастать. Действительно, второй пере-
менной можно придавать сколь угодно большие значения, при
этом ограничения задачи будут выполняться, а целевая функция
неограниченно возрастает.
7.2.3. Способы построения исходного решения
(см.п.3.6)
"Очевидное" исходное опорное решение

140
Задачи линейного программирования в стандартной поста-
новке имеют очевидное исходное опорное решение (см. примеры
7.5, 7.6).
Вспомогательная задача
Для нахождения исходного опорного решения может быть
использована вспомогательная задача, которая ставится в виде
-1
т
x
d
→ max,
A x + E x
d
= b,
x ≥ 0, x
d
≥
.
0.
Рассмотрим пример
Пример 7.7.
-1x
1
+ 1x
2
→ max
1x
1
+ 1x
2
≥ 2
2x
1
- 1x
2
≤ 4
1x
1
+ 4x
2
= 20
x
1
,x
2
≥ 0.
Сведем задачу к каноническому виду
-1x
1
+ 1x
2
→ max
1x
1
+ 1x
2
- 1x
3
= 2
2x
1
- 1x
2
+ 1x
4
= 4
1x
1
+ 4x
2
= 20,
x
1
,...,x
4
.
≥ 0.
Вспомогательная задача, позволяющая найти исходное
опорное решение данной задачи, имеет вид
- x
5
- x
6
- x
7
→ max
1x
1
+ 1x
2
- 1x
3
+ x
5
= 2
2x
1
- 1x
2
+ 1x
4
+ x
6
= 4
1x
1
+ 4x
2
+ x
7
= 20,
x
1
,...,x
7 .
≥ 0.
Решим ее с использованием симплекс-метода. Исходное опорное
решение очевидно: x = (0 0 0 0 2 4 20)
т
.
Итерация 1: δ
k
= -4; k = 1; θ
r
= 2; r = 1.
1
-
26.0 -1.0 -1.0 -1.0 -4.0 -4.0
5 2.0 1.0 0.0 0.0 1.0 1.0
6 4.0 0.0 1.0 0.0 2.0 2.0
7 20.0 0.0 0.0 1.0 1.0 1.0
