Myron G. Best. Igneous and metamorphic 2003 Blackwell Science

Подождите немного. Документ загружается.

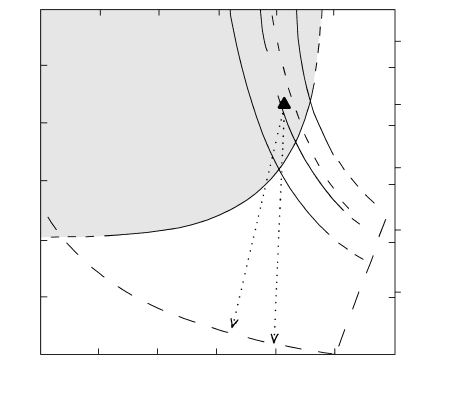
not necessarily, loss of its dissolved water. Though

many explosive pyroclastic eruptions followed the cat-

astrophic May 18, 1980, event, they were of declining

intensity and volume. Meanwhile, a viscous lava dome

slowly extruded from the vent; the magma feeding this

dome is believed to have followed a path indicated by

one of the dotted lines in Figure 5.33.

Experimental studies of the rate of amphibole

breakdown and rim production indicate ascent rates of

15–50 m/h for post–May 18 magma extrusions. These

relatively slow rates would allow some conductive cool-

ing to the wall rocks as well as cooling by the loss of wa-

ter from the magma. In contrast, ascent rates  66 m/h

must have occurred for the explosively erupted May 18

magma in which no reaction rims developed on the am-

phibole phenocrysts.

5.8 GEOTHERMOMETERS AND

GEOBAROMETERS

Determination of intensive parameters in long dead

magma systems using equilibrium assemblages of coex-

isting minerals is a major endeavor of modern petrol-

ogy. Many quantitative mineral geothermometers and

geobarometers have been calibrated by experiment

and thermodynamic models, but a detailed presenta-

tion is beyond the scope of this textbook; only a few

have been brieﬂy introduced. Oxygen fugacity and T

can be determined from coexisting equilibrium mag-

netite and ilmenite solid solutions (Section 3.5.5). T

can be determined from coexisting alkali feldspar and

plagioclase and from clino- and orthopyroxene solid

solutions (Sections 5.5.4 and 5.6). A geobarometer for

determination of P during crystallization of some felsic

magma systems relies on the equilibrium concentration

of Al in hornblende; calibration is sensitive to T, oxy-

gen fugacity, and the crystalline phases coexising with

a water-saturated melt (Anderson and Smith, 1995).

Finally, the water fugacity in a magma can be deter-

mined from an equilibrium assemblage of biotite 

magnetite  K-feldspar (discussed earlier) in a rock if

P, T, and oxygen fugacity can be independently deter-

mined (Bohlen et al., 1980).

5.8.1 Assessing States of Equilibrium in Rocks

Use of mineral geothermometers and geobarometers,

as well as other interpretations of rocks, depends on a

state of stable equilibrium prevailing in the magma sys-

tem when the crystals formed. Mineral compositions

must not have been modiﬁed since that equilibrium

state and must be accurately known, and all relevant

components in the system must be accounted for

(Frost and Lindsley, 1992). Stable equilibrium is gener-

ally assumed in the case of euhedral crystals, which are

bounded on all sides by rational crystal faces, sur-

rounded by glass or aphanitic crystalline material. Such

textures are only necessary, not sufﬁcient, to establish a

state of stable equilibrium. Various tests have been de-

vised to ascertain whether the pair of minerals used in

geothermobarometry are valid representations of equi-

librium.

States of disequilibrium, or metastable phases

frozen into the rock because of sluggish kinetics and in-

complete reaction relations in dynamic magma sys-

tems, are more readily discerned and veriﬁed than

equilibrium states. Disequilibrium states are suggested

by the following:

1. Isolated anhedral (noneuhedral) grains that re-

sulted from partial resorption or dissolution into

the melt.

2. Reaction rims of one or more phases surround-

ing another anhedral crystalline phase. Phaneritic

rocks may have reaction rims of amphibole jacket-

ing pyroxene (Plate II) and biotite surrounding am-

phibole that are created by incomplete reaction re-

lations in a fractionating magma.

3. Compositionally zoned grains also originate through

incomplete reaction relations within a single solid-

solution series, such as plagioclase. Zoning in

plagioclase is obvious in thin sections in cross-

polarized light but in other solid solution crystals is

generally less obvious. In some cases, the outermost

rims of an assemblage of zoned minerals represent

equilibrium precipitates.

Crystal-Melt Equilibria in Magmatic Systems

117

700 800 900 1000

T (°C)

P (kbar)

Depth (km)

Amphibole

Fe-Ti oxides

Cpx

Opx

Water-saturated

liquidus

Dry

solidus

Adiabat

Conductive cooling

Opx + Cpx +

Pl + Fe-Ti oxides

+ melt + fluid

Water-saturated

solidus

5.33 Phase relations for the 1980 dacite of Mount Saint Helens,

Washington. Compare Figure 5.31. Boundary lines (dashed

where approximate) are for P  P

ﬂuid

 P

and oxygen fu-

gacity near the NNO buffer. Stability ﬁeld of the amphibole in

the dacite is shaded. The ﬁlled triangle represents equilibra-

tion conditions in the magma just prior to its paroxysmal erup-

tion of May 18, 1980. Dotted lines are hypothetical paths of

ascending magmas erupted subsequently in the 1980–86 erup-

tions. (Redrawn from Rutherford and Hill, 1993.)

Other indicators of disequilibrium in rocks in-

clude experimentally known unstable or unlikely (in

an evolutionary sense) mineral assemblages: for ex-

ample, a volcanic rock that contains magnesian olivine

and quartz, or magnesian olivine and/or pyroxene

with sanidine, or grains of two distinct compositions

in a single solid-solution series having no miscibility

gap or solvus. Such disequilibrium assemblages com-

monly originate through mixing of two dissimilar

magmas.

5.9 A BRIEF COMMENT REGARDING

SUBSOLIDUS REACTIONS IN

MAGMATIC ROCKS

All magmatic rocks solidiﬁed from magma at high T

must have cooled to near-atmospheric T before a

petrologist studies them. Plutonic rocks must also have

decompressed. At decreasing T, reaction rates are slug-

gish, causing metastable, magmatic phases to persist

well outside their ﬁeld of stability (Section 3.6.2). Sub-

solidus mineral reactions and recrystallization are com-

monly incomplete, leading to states of disequilibrium

that can sometimes be detected by the phase rule. Sec-

ondary, subsolidus mineral grains are typically very

small and not readily identiﬁed even with a micro-

scope.

Cooling volcanic rocks emplaced on the surface of

the Earth are also subjected to a signiﬁcant increase in

oxygen fugacity relative to pristine deep-seated mag-

mas, which are equilibrated generally within a few log

units of the QFM buffer (Figure 3.14). Consequently,

the predominantly ferrous Fe in primary magmatic

minerals and glass is at least partially oxidized to the

ferric state, stabilizing hematite (or at least excess mag-

netite). The tiny grains of secondary hematite redden

Fe-bearing phases, as explained for biotites. Amphi-

boles and biotites also suffer dehydration reactions be-

cause of the decrease in water fugacity that affects

erupted magmas. These subsolidus decomposition ef-

fects may be difﬁcult to distinguish from reaction rela-

tions involving melt above the solidus. However, grain

118 Igneous and Metamorphic Petrology

Advanced Topic Box 5.4 The MELTS com-

puter software model

MELTS is a thermodynamically-based model by

Ghiorso and coworkers (e.g., Ghiorso, 1997) of

crystal-melt equilibria calibrated from thousands of

experiments. The model is menu-driven and inter-

active and computes phase compositions and pro-

portions by minimization of the chemical potential

of magma systems. MELTS models real magmas

crystallizing in either the fractional or equilibrium

way under speciﬁed conditions: initial conditions

and constraints under which the system evolves. For

example, speciﬁcation of P, oxygen fugacity, and

system composition allows one to track as a func-

tion of T the progress of crystallization in a closed

system under equilibrium conditions; evolving solid

and liquid compositions, viscosities, and densities

are output data.

0 0.03mm 0 0.04mm

(a) (b)

5.34 Subsolidus decomposed hornblende phenocrysts. (a) Partially decomposed hornblende with rim of ﬁne-grained Fe-Ti oxides, pyroxenes,

and feldspars. (b) Completely decomposed (pseudomorphed) amphibole in diorite porphyry. Fine-grained breakdown assemblage simi-

lar to that in (a) mimics shape of original mineral.

sizes tend to be larger in reaction rims, whereas sub-

solidus breakdown products are generally very ﬁne-

grained anhydrous and oxidized secondary minerals

jacketing or completely replacing both amphiboles and

biotites (Figure 5.34).

In the plutonic environment, on the other hand,

magmatic rocks generally cool to some extent below

the solidus T before much decompression occurs, per-

haps millions of years later by tectonic uplift and ero-

sional denudation. Therefore, the P-T path followed is

much different, and so is the nature of secondary min-

eralogical changes. As the crystalline plutonic assem-

blage cools, it passes into the stability ﬁelds of lower T,

but elevated P, hydrous phases such as epidote miner-

als and other hydrated Ca-Al silicates, chlorites, and, at

lowest temperatures, clay minerals (Plate IV).

SUMMARY

Crystal-melt equilibria in simple model systems indi-

cate what is possible and impossible in chemically more

complex, multicomponent natural magma systems.

The phase rule can be used to assess states of equilib-

rium and the degrees of freedom in magmatic systems.

For example, both intensive variables may be freely

varied without changing the state of equilibrium in di-

variant stability ﬁelds in P-T or T-X space. Drawing

isopleths, isotherms, and tie lines and applying the

lever rule permit compositions and proportions of co-

existing melt and crystals to be determined in equilib-

rium systems.

Essentially isothermal decompression of initially sub-

solidus water-free rocks can lead to melting, whereas

decompression of water-saturated magmas can cause

crystallization.

Solid solutions, some pure minerals such as ensta-

tite, and polymineralic rocks melt incongruently to

a liquid and crystals whose compositions differ from

that of the starting material. Incongruent melting ac-

counts for much of the diversity of igneous rocks and

the global differentiation of the Earth into crust and

mantle.

Denser crystalline phases are stabilized in magmas

at high P. Under upper mantle conditions, a basalt

magma can contain Mg-rich garnet and a complex Na-

Al-Ca clinopyroxene instead of plagioclase, Ca-Mg-Fe

pyroxene, and olivine.

In crystallizing multicomponent magmas and in

melting source rocks, reaction relations at the ionic

level between liquid and solid solutions continuously

modify their compositions as intensive variables change.

Compounded with kinetic factors in dynamic magma

systems, reaction relations in crystallizing magmas al-

low for a wide range of possible liquid lines of descent

taken by residual melts and reaction series taken by

crystalline products. A signiﬁcant kinetic factor is the

degree to which a magma fractionates during crystal-

lization because reaction relations between melt and

crystals are precluded. Fractionation can occur by

moving the crystal away from the parcel of melt where

it precipitated, by creating a reaction rim about the

metastable crystal, or by changing intensive parameters

in the magma faster than the rate at which reaction

occurs.

Fractionation extends the range of T over which

crystallization takes place, extends the range of residual

melt compositions, and creates more diverse crystalline

products, or reaction series. Liquid lines of descent

produced as solid solutions fractionate are curved on a

variation diagram. More evolved residual melts are

commonly enriched in Si and have greater (Na  K)/

Ca and Fe/(Fe  Mg) ratios.

Volatiles, especially water because of its high solu-

bility in melts, have a profound inﬂuence on crystal-

melt equilibria. By depolymerization of the silicate

melt, liquidus and solidus temperatures are depressed

by as much as several hundreds of degrees. Volatile-

bearing minerals, especially major rock-forming micas

and amphiboles, are stabilized in volatile-rich magmas

but decompose into volatile-free minerals at high T.

Amphibole and biotite stabilization requires 3–5 wt.%

dissolved water in andesite-dacite melts. Stability of Fe-

bearing hydrous minerals such as biotite and amphi-

bole depends on fugacities of H

O, O

, Cl, and F in

addition to P and T. Nonvolatile mineral compositions

can also be inﬂuenced by volatiles; thus, more calcic

plagioclase is stabilized in water-rich magmas. Sub-

solidus decomposition (alteration) of primary high-T

magmatic precipitates yields ﬁne-grained aggregates of

ferric oxides and anhydrous minerals at low water and

high oxygen fugacity in extruded magma and ﬁne-

grained, more hydrous phases in conﬁned plutonic sys-

tems to the extent that water is available.

Under equilibrium conditions in magma and meta-

morphic systems the partitioning of chemical elements

among crystallizing solid solutions depends on the pre-

vailing P and T; hence, compositions of coexisting min-

erals serve as thermobarometers.

CRITICAL THINKING QUESTIONS

5.1 Describe how the phase rule is derived, what it

means, and how it is used in reading phase dia-

grams and interpreting magmatic mineral assem-

blages.

5.2 Contrast the effects of decompressing a mag-

matic system from a P just above the solidus un-

der water-free and water-saturated conditions.

Crystal-Melt Equilibria in Magmatic Systems

119

granitic rocks? (Hint: Write a balanced miner-

alogical reaction involving these three minerals.)

5.17 Is it true that minerals having higher melting

temperatures crystallize from magmas at rela-

tively higher temperatures? Critically evaluate

this by examining the relative melting tempera-

tures of quartz (-form in Figure 5.1), forsterite

olivine, diopside pyroxene, and albite feldspar

(Figure 3.8). With what mineral(s) does quartz

commonly coprecipitate (Figure 2.2)? What re-

ally controls crystallization temperatures of min-

erals from melts?

5.18 On the basis of the concepts of crystal-melt

equilibria set out in this chapter, how should

Figure 3.12 be modiﬁed?

PROBLEMS

5.1 Describe the crystallization and melting of a

bulk composition An

from above the liquidus

and from below the solidus, respectively, in the

CaMgSi

-CaAl

system at 1 atm. What

are the proportions of phases at 1300°C?

5.2 Thousands of basaltic deposits worldwide con-

tain fragments of phaneritic rock composed of

about 65% magnesian olivine, 25% enstatite,

8% diopside, and 2% Mg-Al-Cr spinel. Name

this rock from Chapter 2, recalculate its mode

so that olivine plus enstatite equals 100%, and

draw an appropriate isopleth on Figure 5.8 for

their recalculated proportions. (Because the

densities of the two minerals are nearly the

same, no correction is needed to convert modal

volume into weight percentage.) Because these

fragments are pieces of the upper mantle from

which basalt magmas are derived by partial

melting, describe the melting relations of this re-

calculated model mantle rock. How much melt

is produced at the initial melting T? What is the

composition of the ﬁrst partial melt? How does

it compare in composition with an average

basalt (Table 2.2)?

5.3 Using MELTS (Advanced Topic Box 5.4) on the

Makaopuhi basalt magma, (a) conﬁrm that

residual melts become more enriched in Fe and

Ti until Fe-Ti oxides precipitate; (b) determine

the chemical composition of the residual melt

just above the solidus; (c) track the changing

chemical compositions of major solid solutions

during crystallization. Discuss your results.

5.4 Make photocopies of Figure 5.11. Color the sta-

bility ﬁeld of amphibole. Is amphibole a stable

phase in extruded basalt magmas? Discuss. In

the dry system, contrast (by colors) the stability

ﬁelds with plagioclase and with garnet. What

5.3 Liquidus temperatures in simple binary systems

(e.g., Figures 5.4 and 5.8) used to model multi-

component magma systems are hundreds of de-

grees higher than the temperatures at which liq-

uidus phases precipitate in real magmas (e.g.,

Figures 5.10 and 5.11). Why?

5.4 A liquidus line in a binary phase diagram has

four meanings. Describe them.

5.5 Contrast the state of a water-free and a water-

saturated tholeiite system at 1100°C and 10 kbar

(Figure 5.11).

5.6 Cite two scenarios that would allow a thermally

insulated, water-rich intrusive magma to crystal-

lize rapidly—developing a ﬁne-grained tex-

ture—as if it were extruded onto the surface of

the Earth into the cool atmosphere.

5.7 In a magmatic rock, what compositional as-

pect—modal or mineral—deﬁnes the intensive

parameters prevailing at the time the magma

crystallized? Explain.

5.8 Contrast crystallization in a magma system dom-

inated by a eutectic versus a system in which

continuous reaction relations take place over a

range of P-T conditions. Which has the poten-

tial to develop the most diverse crystalline prod-

ucts? Which do you think prevails in real mag-

mas? Discuss.

5.9 Describe all of the ways in which a crystallizing

magma can fractionate crystals from melt.

5.10 Contrast equilibrium versus fractional crystal-

lization with respect to operative range of T,

range of residual melt compositions, and nature

of crystalline products. Cite examples.

5.11 Describe incongruent melting and its signiﬁcance.

5.12 Account for the contrasting mineralogical com-

positions of basalt and eclogite.

5.13 Why are liquid lines of descent on variation dia-

grams curved for fractionating systems involving

solid solutions?

5.14 Partially resorbed anhedral phenocrysts in vol-

canic rocks are not uncommon. Describe possi-

ble origins in both open and closed magma sys-

tems.

5.15 Contrast the changes in the magmatic system

that created the breakdown of amphibole in

Figures 5.32 and 5.34.

5.16 How common are water-saturated granitic mag-

mas? Most of the experimentally determined

phase relations for granite systems are for water-

saturated conditions. Does this necessarily mean

real magmas are water-saturated? What textures

can be found in water-saturated magmas? What

is the implication of the widespread assemblage

of biotite  alkali feldspar  magnetite in

120 Igneous and Metamorphic Petrology

Crystal-Melt Equilibria in Magmatic Systems

121

controls these contrasting stabilities? What is

the maximum depth to which olivine is stable in

water-free or water-saturated tholeiitic basalt?

How do you reconcile this limited stability of

olivine in basalt relative to what it is in upper

mantle peridotite (Figure 1.3)?

5.5 Prove that the mass balance equation 5.4 is valid

by multiplying the weight percentages of liquid

and crystalline phases by the weight fractions of

the NaAlSi

and CaAl

components on

each side of the equation.

5.6 On a photocopy of Figure 5.27a, draw the path

of a fractionating melt whose initial composition

is 5 wt.% SiO

and 25 wt.% KAlSi

. Con-

struct lines of liquid descent for Na

O and K

versus SiO

for this fractionating melt. Compare

your diagram with Figure 5.27b.

5.7 Sketch the binary KAlSi

-SiO

phase diagram

at 1 atm on the basis of the following informa-

tion: Pure K-feldspar melts incongruently at

1150°C to equal amounts of liquid and leucite

crystals; melting is complete at about 1560°C.

Pure leucite (KAlSi

) melts at 1685°C and

pure silica at 1713°C. A binary eutectic lies at

about 990°C and 54 wt.% silica where a silica

polymorph, K-feldspar, and melt are in equilib-

rium. Describe equilibrium and fractional crys-

tallization of a system that contains 30 wt.%

silica.

5.8 Sketch the phase diagram for the binary system

SiO

(forsterite)-Fe

SiO

(fayalite) at 1 atm

keeping in mind that solid solution is complete,

as it is in the plagioclase system. The melting T

of pure fayalite is 1205°C and of pure forsterite

(Figure 3.8) about 1890°C. Describe the liquid

and crystalline products of perfect fractional

crystallization of a selected melt composition,

including a statement about the Fe/(Fe  Mg)

ratio.

5.9 On a P-T diagram, sketch approximate relative

positions and slopes of liquidus and solidus

curves for a water-saturated granitic magma.

Superpose on this diagram the relative approxi-

mate positions of the breakdown curves for

muscovite, biotite, and hornblende, using the

following observations for guidelines: Pheno-

crysts of muscovite almost never occur in rhyo-

lite, but ﬁne-grained muscovite does form as a

subsolidus alteration product. Primary mus-

covite occurs only in some peraluminous gran-

ites. Biotite and hornblende are common in

granite and as phenocrysts in rhyolite and

dacite. Amphibole is abundant in higher-T

diorites.

5.10 Using Advanced Topic Box 5.2 and Figure 5.7

as guides, draw a sequence of G-X diagrams at

different temperatures for the NaAlSi

CaAl

system.

UNDAMENTAL

UESTIONS

ONSIDERED IN

HIS

HAPTER

1. How do atomic-scale, time-dependent kinetic

phenomena govern changing states of melts? How

do melts ﬂow as viscous liquids?

2. What is viscosity, what factors control the viscosity

of melts, and how does viscosity impact the

dynamic behavior of melts?

3. What is diffusion, what factors control rates of

atomic and thermal diffusion, and how do these

rates impact crystallization and vesiculation of

melts?

4. How do crystals nucleate, grow, and modify their

shape and size?

5. How do exsolved volatile bubbles nucleate, grow,

and fragment melts?

INTRODUCTION

In dynamic magmatic systems, changing intensive pa-

rameters and energy conditions cause the state of the

system to change, but only insofar as kinetic factors al-

low. Thus, the rate at which the T of a magma decreases

is commonly faster than the rate at which kinetically

controlled crystallization can progress, creating com-

positionally zoned crystals and reaction rims in the

fractionating magma. Sluggish kinetic rates prevent ho-

mogenization of the zoned crystal and equilibration via

reaction relations with the enclosing melt, even though

temperatures may be relatively high. Instantaneous

change from an initial metastable state to a new state of

more stable, perfect equilibrium almost never takes

place in magmatic systems because of slow kinetics.

In this chapter, we focus on kinetic factors that

operate on the atomic level in controlling two basic dy-

namic aspects of melts—solidiﬁcation and vesiculation-

fragmentation. Whether the same granitic melt solidi-

ﬁes to a massive metastable glass; to an aphanitic or to

a phaneritic aggregate of quartz, feldspar, and biotite

crystals; to highly vesicular pumice; or to ﬁne ash par-

ticles depends on the interplay between rates of chang-

ing environmental conditions, such as T, and kinetic

(time-dependent) process rates. The nature of the ki-

netic history, or kinetic path, taken by the changing

melt during solidiﬁcation or vesiculation is recorded in

the fabric of the resulting rock, discussed in the fol-

lowing chapter.

Section 3.6 introduced kinetic phenomena. A com-

prehensive treatment is Lasaga (1998).

The ﬁrst three sections of this chapter deal with

three so-called transport phenomena (Figure 6.1):

1. Transport of viscous material, sometimes referred

to as a transfer of momentum (mass  velocity)

2. Transfer of atoms, usually referred to as chemical

diffusion

3. Transfer of heat by conduction (Section 1.1.3)

Each of these three transport processes has a driving

force and a proportionality constant that is an intrinsic

property of the material. Each depends in some way on

the movement of atoms.

6.1 VISCOSITY OF MELTS

On an atomic scale in melts, viscosity is a measure of

the mobility of atoms, how readily atomic bonds can

be stretched, broken, and reformed with neighboring

CHAPTER

Chemical

Dynamics of Melts

and Crystals

Chemical Dynamics of Melts and Crystals

123

atoms. Solidiﬁcation of melts and exsolution of volatile

components from them, which are the two principal

themes of this chapter, involve the movement of atoms,

or the lack thereof. The ease with which atoms can

move about is expressed on a larger macroscopic scale

in a body of material, such as a lava ﬂow, in its resis-

Stationary

plate

Viscous flow

(movement of material)

(a)

6.1 Three transport phenomena. All involve a gradient in some quantity that provides a driving force for transport and all follow similar laws.

(a) Viscous ﬂow in a cube of material (dashed lines) is driven by a force applied tangentially to its upper surface area. This applied shear

stress ( force/area  stress), , produces a change in the shape of the body so that the cube becomes a parallelepiped. The change in shape,

called strain, , becomes more extreme with time, that is, the applied shear stress creates a certain strain rate, d/dt, whose magnitude

depends on the viscosity of the particular material, . The strain rate is equivalent to a velocity gradient, dv/dy, which is shown by arrows

of increasing length over the distance dy. (b) Chemical diffusion is driven by a change in concentration, dc, of some particular atoms be-

tween a region of higher concentration (left face of the cubical volume of material) and lower concentration (right face); these two faces

are separated by a distance, dx. The concentration gradient, dc/dx, produces a ﬂow of atoms, J, down the gradient. (c) Thermal diffusion,

or heat conduction, is driven by a gradient in temperature over a distance, dT/dx, and produces a ﬂow of heat over time, dq/dt. The pro-

portionality constants for these three types of transport are intrinsic properties of the material. For viscous ﬂow the constant is the coef-

ﬁcient of viscosity, or viscosity, ; for chemical diffusion it is the diffusion coefﬁcient, or diffusivity, D; and for heat conduction it is the

thermal conductivity, k.

(b)

Lower

concentration

J = − D

Higher

Chemical diffusion

(movement of atoms)

Cooler

dΤ

−

Hotter

Thermal diffusion

(conductive movement of

thermal energy)

(c)

tance to ﬂow or deformation. On both scales, viscosity

is a manifestation of mobility. Less mobility corre-

sponds to greater viscosity. “Fluidity” and viscosity are

inversely related (opposites).

Unquestionably, viscosity is the most important

property of melts that controls the dynamic behavior of

magmas. Segregation of partial melts in upper mantle

and lower crustal sources, magma ascent to shallower

depths, intrusion, extrusion as lavas or as explosive

fragments, and crystallization all depend on the viscos-

ity of the melt.

Viscosity is formally deﬁned in Figure 6.1a. A force

exerted parallel to the surface area of a viscous body

produces a shear stress,  (stress  force/area), that de-

forms the body by viscous ﬂow in a time-dependent

way. This ﬂow deformation can be measured by a

velocity gradient, dv/dy, or alternatively by a rate of

change in shape, or strain rate, d/dt. The proportion-

ality constant relating the shear stress (the “driving

force”) and the resultant ﬂow is the coefﬁcient of New-

tonian viscosity, 

6.1   



 







For brevity, the coefﬁcient of viscosity can simply be

called the viscosity.

A convenient way to measure viscosity is by deter-

mining how fast a sphere of contrasting density falls or

rises through the material (see Stokes law in Section

8.3.3).

The unit of viscosity is the Pa s (Pascal  second) or

the poise (10 poise  Pa s). Typical viscosities (in Pa s)

include air 10

5

; water 10

3

; honey 10

; cool asphalt

(tar) 10

. Silicate glasses have viscosities  10

. In

terms of its atomic structure, glass is a liquid, but in

terms of its behavior (atomic mobility and capacity to

ﬂow), it is a solid. One way to distinguish between a

solid and a liquid is by the time scale for ﬂow. Liquids,

such as water and honey, can ﬂow appreciably in min-

utes because of low viscosity, whereas solids “ﬂow”

negligibly, or not at all, over periods measured in years.

For example, the solid mantle of the Earth, whose vis-

cosity is on the order of 10

Pa s, convectively ﬂows at

a rate of a few centimeters or less per year, the rate of

plate motion.

The two principal factors governing viscosity of

melts are their composition—as it controls the de-

gree of polymerization—and their T. More polymer-

ized, more silica-rich melts, which have smaller ratios

of nonbridging oxygens to network-forming cations

(Section 4.1.1), are more viscous. Ions cannot move

about readily, especially those that make up polymers,

because the strong Si  O and Al  O bonds must be

stretched or broken. Less polymerized silica-poor

melts and silica-rich melts that contain dissolved

water and/or ﬂuorine have lower viscosities. For any

melt composition, higher T reduces the viscosity by

“loosening” the melt structure through the increased

kinetic energy of the atoms; ionic mobility is en-

hanced.

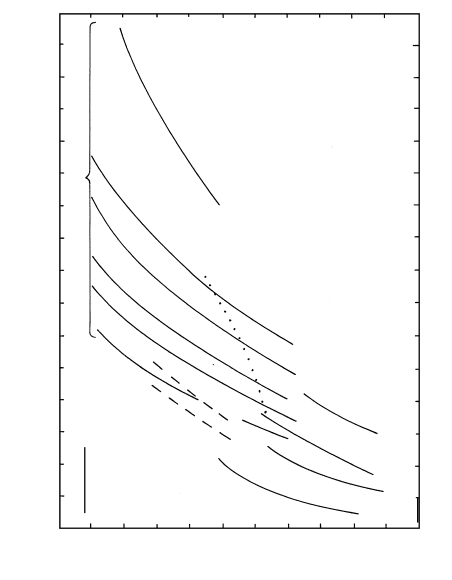
Figure 6.2 illustrates the strong dependence of melt

viscosity on T and composition. For example, the de-

pendence on T is shown by the fact that between

700°C and 1000°C the viscosity of a water-free rhyolite

melt decreases by six orders of magnitude, from about

to 10

Pa s. The dependence on composition is

shown by the fact that there is a difference of about 10

Pa s in viscosities at 1200°C between a silica-poor (46

wt.%) alkali-olivine basalt melt and a silica-rich (77

wt.%) rhyolite melt, both water-free. Besides the silica

concentration factor, dissolved water drastically lowers

the viscosity of highly polymerized, silica-rich melts be-

cause the polymers are broken by hydroxyl ions. Addi-

tion of 6 wt.% water to a rhyolite melt with 77 wt.%

124 Igneous and Metamorphic Petrology

600

−1

800 1000 1200 1400 1600

T (°C)

log

viscosity, η (Pa s)

Alkali

carbonatite

Rhyolite 77 wt. % SiO

74, 76

Andesite 61

Tholeiitic

basalt

Alkali basalt

basalt

~48

Komatiite

6.2 Newtonian viscosities of some crystal- and bubble-free melts

as a function of T at 1 atm. P dependences are negligible. Some

viscosities pertain to metastable melts at temperatures below

their liquidus where they would contain crystals under equi-

librium conditions. Concentrations of silica in weight percent-

age are indicated as well as of water in weight percentage at

low-T end of curves. (Data from Shaw, 1965; Murase and

McBirney, 1973; Webb and Dingwell, 1990; Dawson et al.,

1990; Huppert and Sparks, 1985.) Viscosities for rhyolite

melts that contain 1.5 wt.% ﬂuorine and 6 wt.% water at

10 kbar are dashed lines (peraluminous, 74 wt.% silica; meta-

luminous, 76; peralkaline, 73). (Data from Baker and Vaillan-

court, 1995.) The dotted line indicates the viscosity of residual

melts resulting from fractional crystallization of Makaopuhi

basalt melt (Table 5.1) with 0.5 wt.% water on the QFM

buffer calculated from the MELTS program; the most evolved

melt has 73 wt.% silica and 0.3 wt.% water.

Chemical Dynamics of Melts and Crystals

125

silica at 800°C lowers the viscosity by seven orders of

magnitude, from about 10

to 10

Pa s. Most of the re-

duction in viscosity in hydrous silicic melts occurs in

the ﬁrst 2 wt.% or so of added dissolved water because

that ﬁrst 2% is mostly (OH)



(Section 4.2.2). Dis-

solved water has less effect on basalt melts because they

are less polymerized regardless of volatile content. Dis-

solved ﬂuorine also reduces polymerization and viscos-

ity, but, unlike water, which has very limited solubility

in melts at low P, ﬂuorine can remain in solution in the

melt and can therefore enhance the mobility of lavas

extruded onto the surface of the Earth. Rhyolite melts

having the lowest viscosity are those that contain both

dissolved water and ﬂuorine. The lowest viscosities of

any known terrestrial melts are found in ultramaﬁc

high-T komatiites and essentially silica-free, alkali car-

bonatites extruded at about 585°C from Oldoinyo

Lengai volcano in the East African Rift (Dawson et al.,

1990). The 15 orders of magnitude difference in vis-

cosity between carbonatite and dry rhyolite melts ex-

truded near 600°C is illustrated by the contrasting

morphological characteristics of their extruded lavas—

the former having the appearance of muddy water and

the latter forming steep bulbous domes that can be

higher than their horizontal diameter. Widespread

basaltic lavas that are no more than a couple of orders

of magnitude more viscous than cooler carbonatitie

melts form sheetlike ﬂows, again in striking contrast

with mushroom-shaped rhyolite extrusions.

Melt viscosity is only weakly dependent on P. An

isothermal increase in P of 20 kbar reduces the viscos-

ity of maﬁc melts by less than 50% and silicic melts by

a slightly greater factor (Richet and Bottinga, 1995).

This negative dependence on P follows because bridg-

ing oxygens have a greater molar volume than non-

bridging, and, therefore, from Le Chatelier’s principle,

a positive increment in P increases the ratio of non-

bridging to bridging oxygens that depolymerizes the

melt, reducing the viscosity.

The viscosity of melts that carry suspended crystals

(i.e., magma) and contain bubbles of volatile ﬂuid, as

well as those that have an intrinsic yield strength do not

follow the form of Equation 6.1 (see Section 8.2.2 for a

discussion of non-Newtonian magmas).

If a melt is deformed slowly, its distorted atomic

structure has time to adjust or relax; it behaves as a liq-

uid. However, for increasingly rapid deformation (in-

creasing strain rate) at constant T, particularly in cooler

more viscous polymerized melts, the melt crosses a

threshold between liquid and solid behavior, called the

glass transition, deﬁned as the T at which 10

Pa s.

If rapid deformation takes place at viscosities above

this glass transition, the melt cannot adjust: its relax-

ation “time” is exceeded. It behaves as if it were a

solid, breaking as any brittle solid does if the applied

stress is excessive.

Advanced Topic Box 6.1 Calculation of

melt viscosity

Shaw (1972) developed a model from which the

viscosity of homogeneous melts can be calculated

from their chemical composition. This model as-

sumes the viscosity follows an Arrhenius relation

  A exp (E

/RT) where A is a constant, E

the activation energy of viscous ﬂow, R is the gas

constant, and T is in degrees Kelvin. Although many

melts depart to varying degrees from Arrhenian be-

havior, Shaw’s model has nonetheless proved useful.

The full details cannot be dealt with here; only a

“cookbook” presentation is given. The viscosity,

, is found from the equation

2.303 log

s(10

/T)  1.5s  6.4

For example, calculation of the viscosity of a

hydrous rhyolite (granite) melt at T  1073K

(800°C) is presented in Table 6.1, where determi-

nation of the value of s is described (minor con-

stituents, such as MnO and P

, are ignored).

Numbers in the Moles column are found by di-

viding the Wt.% values by the Formula wt. of

the corresponding oxide. Note that the moles of

and Fe

are doubled. The mole fraction,

X, is found by dividing the Moles value by the

sum of Moles, or 1.908. In the next column, X

, the

mole fractions of Fe

, FeO, and MgO are added

together (giving 0.009), as are CaO and TiO

(0.004), and Na

O and K

O (0.057). Shaw’s values

of the partial molar activation energies of SiO

binary systems with categories of other oxides, s

are listed in the next column. These values multi-

plied by the mole fraction of SiO

in the particular

melt are listed in the s

SiO

column. Finally, at the

bottom of Table 6.1, the sum of the X

SiO

)

values listed in the last column is divided by (1 

SiO

) to give s, which is inserted into the viscosity

equation. The viscosity calculated from this equa-

tion is 10

5.24

poise  10

4.24

Pa s. The viscosity mea-

sured by Shaw (reference in his 1972 paper) is

4.63

Pa s.

Hess and Dingwell (1996) and Baker (1996) have

devised models based on experimental data that ac-

count for the non-Arrhenian T dependence of vis-

cosity for hydrous rhyolite (granite) melts.

In the Shaw, Hess-Dingwell, and Baker models

no dependence on P is included, as this is negli-

gible.

Ryan and Blevins (1987) have compiled experi-

mentally determined viscosities of a wide range of

melt compositions.

6.2 CHEMICAL DIFFUSION

Diffusion, the second transport phenomenon (Figure

6.1b), is the movement of individual atoms or molecules

through a group of atoms and driven by a concentration

gradient. The material in which atoms are moving does

not itself necessarily move. Atoms and molecules diffuse

quickly through gaseous bodies where the atoms are

widely separated and loosely associated; for example,

aromatic molecules from brewing coffee disperse many

meters in minutes into the surrounding air. Diffusion is

much slower in a liquid and depends strongly on its vis-

cosity and T; higher T expands the atomic structure and,

together with lower viscosity, allows greater freedom of

movement for diffusing atoms. Diffusion is still slower in

solids where atoms are tightly bonded and have limited

kinetic motion relative to those in liquids.

Bowen (1921) ﬁrst drew attention to the signiﬁcance

of diffusion in magma systems. But it was not until a

half-century later, beginning with Shaw (1974), that

other experimental petrologists began to explore this

important transport process.

Diffusion plays many roles in petrologic processes,

some of which are growth of crystals from melts and

other multicomponent solutions, exsolution of vola-

tiles from a melt, reaction relations between melt and

crystals to produce equilibrium compositions among

major as well as trace elements, mixing and contamina-

tion of magmas, and isotopic exchange between crys-

tals and ﬂuids. Because the distance over which diffu-

sion takes place depends on time and T, measurement

of small-scale compositional inhomogeneities within

rock-forming minerals and glasses, such as by an elec-

tron microprobe, can provide important constraints on

their thermal history if the relevant diffusional proper-

ties are known. The closure temperature at which

T-dependent diffusion effectively ceases, or becomes

nil in a geologic time frame, must be taken into account

in interpreting isotopic ages, mineral geothermometers

and geobarometers, and any other aspect of a “frozen-

in” state of compositional equilibrium.

If rates of diffusion (and other kinetic processes)

were inﬁnitely fast, thermodynamic equilibrium would

be accomplished instantaneously as changes in inten-

sive variables occurred. However, diffusion is slow in

melts and can be extremely slow in crystals, so that ves-

tiges or relics of prior states may be preserved in mag-

matic rocks. Fortunately for the petrologist, sluggish

rates of diffusion can provide insights into prior

metastable states and make possible inferences about

petrologic history.

6.2.1 Types of Diffusion

Three routes of diffusion are possible in an aggregate

of mineral grains, a rock.

1. Surface diffusion occurs essentially over a two-

dimensional surface area, but generally has a com-

ponent of atomic movement in the third dimension.

Thus, ions can move about over the free surface of

a mineral grain through a static liquid in contact

with it.

2. Grain-boundary (intergranular) diffusion occurs

along mutual boundaries between contacting min-

eral grains. Because of the hindering effects of the

adjacent grain, diffusion is slower than for surface

diffusion, though both utilize the exterior of a

grain. A very thin ﬁlm of ﬂuid along grain bound-

aries may facilitate diffusion.

3. Volume diffusion occurs within any single homoge-

neous phase, such as a crystal or a melt body. Vol-

ume diffusion through solids is generally the slow-

126 Igneous and Metamorphic Petrology

Table 6.1 Calculation of the viscosity of a hydrous rhyolite melt at 1073K as described in

Advanced Topic Box 6.1.

.% F

ORMULA

OLES

SiO

Xi(

SiO

)

SiO

71.90 60.085 1.195 0.627

12.15 101.961 0.238 0.125 0.125 6.7 4.201 0.525

0.57 159.692 0.007 0.004 0.009 3.4 2.132 0.019

FeO 0.52 71.846 0.007 0.004

MgO 0.04 40.311 0.001 0.001

CaO 0.27 56.079 0.005 0.003 0.004 4.5 2.82 0.011

TiO

0.09 79.899 0.001 0.001

O 3.94 61.999 0.064 0.033 0.057 2.8 1.756 0.100

O 4.32 94.203 0.046 0.024

O 6.20 18.015 0.344 0.180 0.180 2.0 1.254 0.226

SUM 100.00 1.908 0.881

s  [ X

SiO

)]  (1  X

SiO

)  0.881  0.373  2.362. 2.303 log

s (10

/T)  1.5s  6.4  2.362 (10

/1073)  (1.5  2.362)  6.4  12.07.

10

5.24

poise  10

4.24

Pa s.

Data from Shaw (1972).